티쏘 인스타트릭스
Tissot's indicatrix

카르토그래피에서 티소트의 인디카트릭스(Tissot incatatrix, Tissot의 타원, Tissot의 타원, 왜곡의 타원)는 지도 투영으로 인한 국부 왜곡의 특성을 나타내기 위해 1859년과 1871년 프랑스의 수학자 니콜라스 아우구스트 티소트가 제시한 수학 연대표다. 지구와 같은 곡선 기하학적 모델에서 극소수 반지름의 원을 지도에 투영함으로써 생기는 기하학이다. 티쏘는 결과 도표가 지도상의 그 지점에서 축이 최대이고 최소인 두 개의 주요 방향을 나타내는 타원형임을 증명했다.
단일 인디케이터릭스는 단일 지점에서 왜곡을 설명한다. 왜곡은 지도에 따라 다르기 때문에, 일반적으로 Tissot의 지시문은 왜곡의 공간적 변화를 나타내기 위해 지도에 걸쳐 배치된다. 일반적인 계획은 표시된 경혈과 평행의 각 교차점에 그들을 배치한다. 이러한 도식은 왜곡을 예시하고 각 지점에서 정확하게 왜곡의 크기를 나타내는 계산의 근거를 제공하기 위해 지도 투영 연구에 중요하다.
Tissot 인디카트릭스와 지도 투영 좌표 변환의 미터법 텐서 사이에는 일대일 일치성이 있다.[1]
설명
티소트의 이론은 지도학 분석의 맥락에서 발전되었다. 일반적으로 기하학적 모형은 지구를 나타내며 구체나 타원형의 형태로 나온다.
Tissot의 지표는 지도에 선형, 각도 및 영역 왜곡을 나타낸다.
- 지도는 투영 표면에 투영된 것처럼 무한히 짧은 선의 길이와 원래 지구 모델에 있는 것처럼 거리(선형 왜곡)가 1에서 벗어나는 곳이면 거리(선형 왜곡)를 왜곡한다. 그 지수를 척도계수라고 한다. 고려되는 지점에서 투영이 등각되지 않는 한, 스케일 계수는 점 주위의 방향에 따라 달라진다.
- 지도는 지구의 모델에서 측정된 각도가 투영에서 보존되지 않는 곳마다 각도를 왜곡한다. 이것은 원이 아닌 왜곡의 타원에 의해 표현된다.
- 지도는 지구의 모델에서 측정된 영역이 투영에서 보존되지 않는 모든 영역을 왜곡한다. 이것은 지도에 걸쳐 영역이 다른 왜곡의 줄임말로 표현된다.
각 점이 기하학적 모델에서 투영된 각도를 보존하는 등각 지도에서 티소트의 지시자는 모두 위치에 따라 크기가 다양한 원이며, 방향도 다를 수 있다(경맥과 평행으로 분할된 네 개의 원 사분면에 따라). 물체들 사이의 면적 비율이 보존되는 동일한 영역 투영에서 티소트의 지시자는 모양과 방향은 위치에 따라 다르지만 모두 동일한 영역을 가진다. 임의의 투영에서는 영역과 모양 모두 지도에 따라 다르다.
| 보여 주다몇 가지 일반적인 예측에서 Tissot의 지표들을 비교한 세계 지도 |
|---|
수학
인접한 이미지에서 ABCD는 지구의 구형 또는 타원형 모델에 정의된 단위 면적을 가진 원이며, A aB′C′D′는 티소트의 지표면 투영에서 비롯되는 원이다. 세그먼트 OA는 OA′에서 변형되며, 세그먼트 OB는 OB′로 변환된다. OA′은 OA와 같지 않고 OB ob은 OB와 같지 않기 때문에 선형 스케일은 이 두 방향을 따라 보존되지 않는다. 단위 면적 원 내 각도 MOA는 왜곡 타원 내 각도 M′OA로 변환된다. M′OA′ ≠ MOA가 있기 때문에 우리는 각도 왜곡이 있다는 것을 알고 있다. 원 ABCD의 면적은 정의상 1과 같다. 타원 A′B′의 면적이 1보다 작기 때문에 면적의 왜곡이 발생한 것이다.
티소트 인디케이터릭스를 다룰 때, 다른 개념의 반지름이 작용한다. 첫 번째는 원형의 극소수 반지름이다. 결과적인 왜곡의 타원 또한 극소수의 반지름을 가질 것이지만, 미분들의 수학에 의해 이러한 극소수의 값의 비율은 유한하다. 따라서 예를 들어, 왜곡의 결과 타원이 구에 있는 것과 같은 무한대의 크기라면, 그 반경은 1로 간주된다. 마지막으로 인스타트릭스가 지도에서 사람 검사를 위해 그려지는 크기는 임의적이다. 지도에 일련의 지시선을 그릴 때, 그것들은 모두 크기가 비례적으로 정확하도록 동일한 임의의 양만큼 크기가 조정된다.
다이어그램의 M과 같이, 평행선을 따라 자오선을 따라 있는 O로부터의 축은 투영할 때 길이 변경과 회전을 겪을 수 있다. 문헌에서는 주어진 점에 대해 자오선을 따라 척도를 h로, 평행선을 따라 척도를 k로 나타내는 것이 일반적이다. 마찬가지로 자오선과 평행도 사이의 각도가 90°에서 일부 다른 값으로 바뀌었을 수 있다. 실제로 지도가 정합하지 않는 한 타원의 반장축과 반장축에 의해 소계된 각도를 제외한 모든 각도가 변경되었을 수 있다. 특정 각도가 가장 많이 변화할 것이며, 그 최대 변화의 값은 θ′으로 표시된 각도 변형이라고 알려져 있다. 일반적으로 왜곡 분석에서는 어떤 각도인지, 어떤 방향으로 향하는지 잘 알 수 없다. 중요한 것은 변화의 가치다. h, k, θ의 값은 다음과 같이 계산할 수 있다.[2]: 24
여기서 φ과 λ은 위도와 경도, x와 y는 투영 좌표, R은 지구 반지름이다.
결과 a와 b는 지점의 최대 및 최소 척도 인자를 나타내며, 이는 티소타 타원의 반조르 및 반소르 축과 동일하며, s는 면적의 인플레이션 또는 디플레이션의 양(∙ b)을 나타내며, Ω은 지점의 최대 각도 왜곡을 나타낸다.
메르카토르 투영과 기타 모든 등각 투영의 경우, 각 타원이 원 모양으로 변하며 반지름 h = k는 해당 지점에서 어떤 방향으로든 척도 인자와 동일하도록 한다.
정현상 투영과 그 밖의 모든 동일 면적 투영의 경우 타원의 반주축은 반미너 축의 역수로서, 모든 타원이 편심도가 다르더라도 동일한 면적을 갖도록 한다.
임의의 투영의 경우, 타원의 형태나 영역은 일반적으로 서로 연관되어 있지 않다.[3]
수치 계산을 위한 대안적 파생
티소트의 인디카트릭스를 이해하고 도출하는 또 다른 방법은 표면의 차등 기하학을 통해서이다.[4] Tissot의 인디카트릭스의 매개변수는 단수값 분해(SVD)와 중심 차이 근사치를 사용하여 계산할 수 있기 때문에 이 접근방식은 현대적인 수치적 방법에 잘 적합하다.
타원체에서의 미분 거리
타원체에서 3D X {\{\X}}을(를 다음과 같이 파라미터로 지정하도록 하십시오.
여기서 ( ,) 은 각각 경도 및 이며, N }은 적도 R 및 e{\의 함수
거리 요소인 s 은(는) 첫 번째 기본 형식으로 정의된다.
계수는 다음과 같이 정의된다.
필요한 파생상품을 계산하면 다음과 같은 이점을 얻을 수 있다.
여기서 은 적도 반지름, 및 타원체 편심률 의 함수
이러한 값을 첫 번째 기본 형태로 대체하면 타원체에서의 원소 거리에 대한 공식은 다음과 같다.
이 결과는 구면 좌표계의 함수로서 타원체 표면의 거리 측도와 관련이 있다.
거리 요소 변환
티소트의 인디케이터릭스의 목적은 평면 표면에 매핑되었을 때 구의 거리가 어떻게 변하는지 연관시키는 것임을 상기하라. 구체적으로 원하는 관계는 에서 구면 좌표계의 베이스를 따라 다른 거리와 구면 좌표계의 베이스를 따라 다른 거리를 연결하는 변환 T {\이다 이는 다음과 같은 관계에 의해 표현될 수 있다.
여기서 (, ) displaystyle ds(\ 및 ( 0, ) {\은 각각 세로 및 위도 축을 따라 s 의 연산을 나타낸다. (, 0) 및 (, ) 의 연산은 위의 방정식에서 직접 수행할 수 있으며, 다음과 같은 결과를 얻을 수 있다.
이 계산을 위해 이 관계를 행렬 연산으로 표현하는 것이 유용하다.
이제 타원체 표면의 거리를 평면의 거리와 연관시키기 위해서는 좌표계를 연관시킬 필요가 있다. 체인 규칙에서 우리는 다음과 같이 쓸 수 있다.
여기서 J는 Jacobian 행렬이다.
및 에 대한 행렬 식을 연결하면 다음과 같은 지시자로 표시되는 변환 의 정의가 얻어진다.
이 변환 는 타원체 표면에서 평면까지의 매핑을 캡슐화한다. 이 형태로 표현된 SVD는 국부적 변환의 중요한 구성요소를 구분하는 데 사용될 수 있다.
수치 연산 및 SVD
원하는 왜곡 정보를 추출하기 위해 구형 좌표계의 임의의 위치에서 값을 직접 계산할 수 있다. Jacobian, 은 매핑 기능 자체에서 분석적으로 계산할 수 있지만, 중앙의 차이를 이용하여 지도 상의 어느 위치에서든 수치적으로 값을 근사하는 것이 더 간단한 경우가 많다. 이 값들이 계산되면 SVD를 각 변환 매트릭스에 적용하여 국소 왜곡 정보를 추출할 수 있다. 왜곡은 국지적이기 때문에 지도상의 모든 위치에는 고유한 변형이 있다는 것을 기억하십시오.
SVD의 정의를 상기하십시오.
It is the decomposition of the transformation, , into a rotation in the source domain (i.e. the ellipsoid surface), , a scaling along the basis, , and a subsequent second rotation, . For understanding distort이온, 첫 번째 회전은 원의 축을 회전시키지만 타원의 최종 방향과는 관계가 없기 때문에 무관하다. 대각선 단수값 매트릭스로 대표되는 다음 연산은 원형의 축을 따라 원의 스케일을 조정하여 타원형으로 변형시킨다. 따라서 단수 값은 타원의 축을 따라 축척 인자를 나타낸다. 첫 번째 단수 값은 반주축인 스타일 을를) 제공하고, 두 번째 단수 값은 왜곡의 방향 스케일링 요인인 반주축 b을를) 제공한다. 척도 왜곡은 타원의인 b {\ 의 결정요인에 의해 동등하게 계산할 수 있다 마지막으로, 타원의 방향, 은의 첫 번째 열에서 다음과 같이 추출할 수 있다.
갤러리
Tissot의 지시계가 있는 가로 메르카토르 투영법
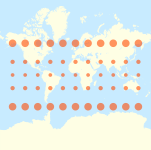
Tissot의 지시문이 있는 입체 투영법
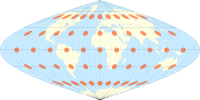
티소트의 지시계가 있는 사인파 투영법
Tissot의 지표가 있는 Peirce Quincitical 투영법
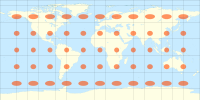
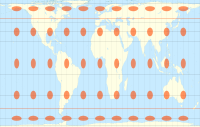
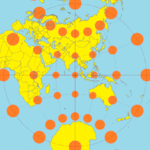
티소트의 지시계가 있는 밀러 원통형 투영법
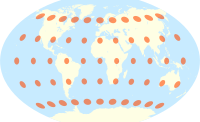
Tissot의 지시계가 있는 해머 투영법
방위각 등거리 투영과 티소트의 지시점
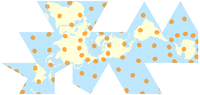
Tissot의 지표가 있는 풀러 투영법
참고 항목
참조
- ^ Goldberg, David M.; Gott III, J. Richard (2007). "Flexion and Skewness in Map Projections of the Earth" (PDF). Cartographica. 42 (4): 297–318. arXiv:astro-ph/0608501. doi:10.3138/carto.42.4.297. S2CID 11359702. Retrieved 2011-11-14.
- ^ Snyder, John P. (1987). Map projections—A working manual. Professional Paper 1395. Denver: USGS. p. 383. ISBN 978-1782662228. Retrieved 2015-11-26.
- ^ Tissot의 인디카트릭스의 더 일반적인 예: Winkel triple 투영법.
- ^ Laskowski, Piotr (1989). "The Traditional and Modern Look at Tissot's Indicatrix". The American Cartographer. 16 (2): 123–133. doi:10.1559/152304089783875497.
외부 링크
| 위키미디어 커먼스는 티쏘의 인디카트릭스와 함께 맵 투영과 관련된 미디어를 보유하고 있다. |








![{\displaystyle {\hat {X}}(\lambda ,\phi )=\left[{\begin{matrix}N\cos {\lambda }\cos {\phi }\\-N(1-e^{2})\sin {\phi }\\N\sin {\lambda }\cos {\phi }\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7bc8b2688a0fccbadec6fc365b948cfe086e137)
 각각 경도 및
각각 경도 및 






![{\displaystyle {\frac {\partial {\hat {X}}}{\partial \lambda }}=\left[{\begin{matrix}-N\sin {\lambda }\cos {\phi }\\0\\N\cos {\lambda }\cos {\phi }\end{matrix}}\right]\qquad \qquad {\frac {\partial {\hat {X}}}{\partial \phi }}=\left[{\begin{matrix}-M\cos {\lambda }\sin {\phi }\\-M\cos {\phi }\\M\sin {\lambda }\sin {\phi }\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4371cb1385e98562f6ba8e02c5715ea7025cb01)
 적도 반지름,
적도 반지름, 






















 으)
으)










