램버트 방위 등면적 투영

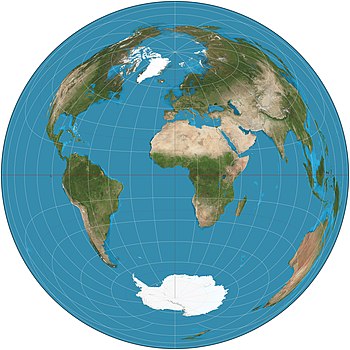
Lambert 방위각 등면적 투영은 구체에서 디스크로의 특정 매핑이다.구체의 모든 영역에서 영역을 정확하게 표현하지만, 각도를 정확하게 표현하지는 못한다.1772년 발표한 스위스 수학자 요한 하인리히 램버트의 이름이다.^[1]"제니탈"은 "아지무탈"과 동의어로서, 투영법은 램버트 정점 등면적 투영으로도 알려져 있다.^[2]

Lambert 방위각 투영은 지도 기록에서 지도 투영으로 사용된다.예를 들어 미국 국립 아틀라스는 램버트 방위각 등면적 투영법을 사용해 온라인 맵 메이커 어플리케이션에 정보를 표시하며, 유럽 환경청은 통계 분석과 디스플레이를 위한 유럽 지도 제작에 사용을 권고한다.^[3][4]3차원 공간에서 선의 방향을 그리는 지질학 등 과학 분야에서도 사용된다.이 플롯은 슈미트 그물이라고 불리는 특별한 종류의 그래프 종이에 의해 도움을 받는다.^[5]

정의

램버트 방위각 투영을 정의하려면 구면의 S 지점에서 구에 접하는 평면을 상상해 보십시오.P를 S의 대척점 이외의 구의 어떤 점으로 한다. d는 3차원 공간에서의 S와 P 사이의 거리(구 표면을 따라가는 거리가 아님)가 되도록 한다.그런 다음 투영은 P를 S로부터 d 거리인 평면의 P ′ 점으로 보낸다.

이를 보다 정밀하게 하기 위해 S를 중심으로 P를 통과하고 평면에 수직인 독특한 원이 있다.그것은 두 점으로 평면을 교차한다; P가 P에 더 가까운 것이 되게 한다.이것이 투영점이다.수치를 보아라.S의 대척점은 필요한 원이 고유하지 않기 때문에 투영에서 제외된다.S의 경우는 퇴보한다; S는 반지름 0의 원을 따라 스스로 투영된다.^[6]

컴퓨터에서 투영 작업을 수행하려면 명시적 수식이 필요하다.x² + y²² + z = 1과 같은 3차원 공간 R의³ 점 집합(x, y, z)인 단위 구체에서 S = (0, 0, -1)에 집중된 투영을 고려한다.구상의 데카르트 좌표(x, y, z)와 평면의 (X, Y)에서 투영과 그 역은 다음으로 설명된다.

${\displaystyle {\begin{aligned}(X,Y)&=\left({\sqrt {\frac {2}{1-z}}}\,x,{\sqrt {\frac {2}{1-z}}}\,y\right),\\(x,y,z)&=\left({\sqrt {1-{\frac {X^{2}+Y^{2}}:{4}}}\,X,{\sqrt{1-{\frac{X^{2}+Y^{2}}{4}}}\,Y,-1+{\frac{X^{2}+Y^{2}}:{2}}\오른쪽).\end{정렬}}}$

구체의 구형 좌표( (, θ)와 원반의 극좌표(R, θ)에서 지도와 그 역은 다음과 같이 주어진다.

${\displaystyle {\begin{aligned}(R,\Theta )&=\left({\sqrt {2}}\sin {\tfrac {1}{2}}\psi ,\theta \right),\\(\psi ,\theta )&=\left(2\arcsin {\tfrac {\sqrt {2}}{2}}R,\Theta \right).\end{정렬}}}$

구의 원통형 좌표(r, θ, z)와 평면상의 극좌표(R, θ, z)에서 지도와 그 역은 다음과 같이 주어진다.

${\displaystyle {\begin{aligned}(R,\Theta )&=\left({\sqrt {2(1+z)}},\theta \right),\\(r,\theta ,z)&=\left(R{\sqrt {1-{\frac {R^{2}}{4}}}},\Theta ,-1+{\frac {R^{2}}{2}}\right).\end{정렬}}}$

투영은 다른 지점에서 중심에 배치될 수 있으며 유사한 공식을 사용하여 반경 1 이외의 구에 정의될 수 있다.^[7]

특성.

앞의 절에서 정의한 바와 같이 단위 구체의 램버트 방위각 투영은 (0, 0, 1)에서 정의되지 않는다.나머지 구를 평면의 원점(0, 0)을 중심으로 반지름 2의 열린 원반으로 보낸다.점(0, 0, -1)을 (0, 0)으로, 적도 z = 0을 (0, 0을 중심으로) 반경의 원, 하반구 z < 0을 그 원 안에 들어 있는 열린 원반으로 보낸다.

투영법은 구(minus (0, 0, 1)와 반지름 2의 열린 원반 사이의 차이점형(양방향에서 무한히 차이가 나는 바이어스)이다.면적보존(동등면적) 지도인데, 투영의 역에 의해 파라메트리했을 때 구의 면적 요소를 계산하면 알 수 있다.데카르트 좌표에서는

$dA=dX\;dY.}$

이것은 구체에서 지역의 면적을 측정하는 것이 디스크에서 해당 지역의 면적을 측정하는 것과 같다는 것을 의미한다.

반면에 투영법은 구의 곡선들 사이의 각도 관계를 보존하지 않는다.구와 평면의 일부 사이의 매핑은 각도와 영역을 모두 보존할 수 없다.(만약 그렇다면, 그것은 국부 등위법일 것이고 가우스 곡면성을 보존할 것이다; 그러나 구와 원반은 다른 곡선을 가지고 있기 때문에 이것은 불가능하다.)평평한 그림이 구의 영역을 완벽하게 표현할 수 없다는 이 사실은 지도학의 근본적인 문제다.

결과적으로, 구체의 영역은 크게 왜곡된 형상으로 평면에 투영될 수 있다.이러한 왜곡은 특히 투영 중심(0, 0, -1)에서 멀리 떨어져 있다.실제로 투영은 종종 그 지점에서 중심을 맞춘 반구로 제한된다. 다른 반구는 대척점에 중심을 둔 두 번째 투영을 사용하여 별도로 매핑할 수 있다.

적용들

램버트 방위각 투영은 원래 동일 영역 지도 투영으로 구상되었다.그것은 또한 다음과 같이 방향 데이터를 그리는 지질학과 같은 분야에서도 사용된다.

3차원 공간의 방향은 원점을 통과하는 선에 해당한다.그러한 모든 행들의 집합은 그 자체로 수학에서 실제 투영면이라고 불리는 공간이다.원점을 통과하는 모든 선은 정확히 두 지점에서 단위 구를 교차하며, 그 중 하나는 하반구 z ≤ 0에 있다(수평선은 두 개의 항정신대 지점에서 적도 z = 0을 교차한다.적도의 항정신병 지점은 하나의 선을 나타낸다고 이해된다.지수 토폴로지를 참조하십시오.)따라서 3차원 공간의 방향은 하반구의 지점과 거의 완벽하게 일치한다.그런 다음 반구는 램버트 방위각 투영을 사용하여 반경 √2의 원반으로 표시할 수 있다.

그러므로 램버트 방위각 투영법은 디스크의 점으로서 방향을 그릴 수 있게 해준다.투영의 동일한 면적 특성 때문에 디스크의 해당 영역 위로 통합함으로써 실제 투영 평면의 영역(방향 공간)에 걸쳐 통합할 수 있다.이는 무작위 강성 회전을 ^[6]포함한 방향 데이터의 통계 분석에 유용하다.^[8]

선뿐만 아니라 원점을 통과하는 평면도 램버트 방위 투영으로 표시할 수 있다.평면은 원반구를 가로지르는 원호(원형이 아닌 원곡선)로 투영하는 면의 흔적이라 불리는 원호(원형 원형이 아닌 원호)로 반구는 원반구의 곡선(일반적으로 원형이 아닌 곡선)까지 투영된다.이 곡선을 그릴 수도 있고, 또는 기둥이라 불리는 수직의 선으로 평면을 교체할 수도 있고, 대신 그 선을 그릴 수도 있다.많은 평면이 함께 플롯되고 있을 때, 트레이스 대신 폴을 플롯하면 덜 어수선한 플롯이 만들어진다.

구조 지질학 연구자들은 램버트 방위각 투영법을 사용하여 결정학적 축과 얼굴, 암석의 선과 엽, 결함의 미끈미끈화, 기타 선형 및 평면 형상을 그린다.이 맥락에서 투영을 동일한 면적 반구형 투영이라고 한다.입체 투영으로 정의한 등각 반구형 투영법도 있다.^[6]

여기서 논의된 내용은 하반구 z might 0(별도표에서 볼 수 있는 바와 같이)의 내부를 강조했지만, 일부 분야(카토그래피 등)는 상반구 z ≥ 0의 외부를 선호한다.^[6]실제로, 어떤 반구라도 3차원 공간에서 기원을 통해 선을 기록하는 데 사용될 수 있다.

애니메이션 램버트 투영

^{[필요하다]}

Let ${\displaystyle (u,\phi )}$ be two parameters for which ${\displaystyle -1<u\leq 1}$ and ${\displaystyle 0\leq \phi <2\pi }$. Let ${\displaystyle H}$ be a "time" parameter (equal to the height, or vertical thickness, of the shell in the animation).균일한 직사각형 그리드가${\displaystyle }$(${\displaystyle u}$, ${\displaystyle \varphi }$) ${\displaystyle (u,\phi )}$ 공간에$$ 그려진 경우, 이 그리드의 모든 지점은 매핑에 따라$$ 높이 $H{\displaystyle }$ ${\displaystyle H}$의 구형 쉘에 있는$$ 점$(x$, $y$, z${\displaystyle }$)으로 변환된다.

$[\displaystyle x=\lambda (u,H)\cos(\phi )}$

$[\displaystyle y=\lambda (u,H)\sin(\phi )}$

${\displaystyle z={\frac {Hu}{2}}:}$

where ${\displaystyle \lambda (u,H)={\frac {1}{2}}{\sqrt {(1-u)\left[8-H^{2}(1-u)\right]}}}$. Each frame in the animation corresponds to a parametric plot of the deformed grid at a fixed value of the shell height ${\displaystyle H}$ (ranging from 0 to 2).물리적으로 $\lambda {\displaystyle }$ ${\displaystyle \lambda }$은(는) 최소 선 $d{\displaystyle }$ ${\displaystyle \varphi }$ ${\displaystyle d\pi }$ 선 세그먼트의 스트레치(형식 길이를 초기 길이로 나눈 값)이다$$.이 매핑은 $z{\displaystyle }$= ${\displaystyle \frac{\mathrm{H}}{}}$( 1 -${\displaystyle \frac{}{\mathrm{}}}$ ${\displaystyle \frac{)}{}}$ 2${\displaystyle }$. ${\displaystyle$ z$={\frac {H(1-u)}{2}$를 대신 사용하여 남극을 고정하는 매핑으로 변환할 수 있다.$}$

$({\displaystyle u}$, ${\displaystyle \varphi }$, H$){\displaystyle (u,\phi ,H$의 값과 관계없이, 이 매핑의 Jacobian은 어디에나 1과 같으며, 애니메이션 전체에 걸쳐 정말로 동일한 영역 매핑임을 보여준다.이 일반화된 매핑은 $H{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle H=0}$일 때 램버트 투영을 특별한 사례로 포함한다$.$

응용 프로그램: 이 매핑은 그리드 셀로 둘러싸인 영역을 변경하지 않고 극에서 구체의 "열림"을 보여줌으로써 램버트 투영의 의미를 설명하는 데 도움이 될 수 있다.

참고 항목

위키미디어 커먼즈에는 램버트 방위각 등면적 투영과 관련된 미디어가 있다.

• 지도 투영 목록
• 방위각 등거리 투영법
• 유럽 그리드
• 해머 투영

참조

원천

• Borradaile, Graham J. (2003). Statistics of Earth science data. Berlin: Springer-Verlag. ISBN 3-540-43603-0.
• Do Carmo; Manfredo P. (1976). Differential geometry of curves and surfaces. Englewood Cliffs, New Jersey: Prentice Hall. ISBN 0-13-212589-7.
• Hobbs, Bruce E., Means, Winthrop D., and Williams, Paul F. (1976). An outline of structural geology. New York: John Wiley & Sons, Inc. ISBN 0-471-40156-0.{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크)
• Ramsay, John G. (1967). Folding and fracturing of rocks. New York: McGraw-Hill.
• Spivak, Michael (1999). A comprehensive introduction to differential geometry. Houston, Texas: Publish or Perish. ISBN 0-914098-70-5.

외부 링크

• 다이어그램과 함께 정렬된 변환에 대한 설명
• 위키미디어 커먼스의 램버트 방위각 등면적 투영과 관련된 매체