호만 전이 궤도
Hohmann transfer orbit| 다음에 대한 시리즈 일부 |
| 아스트로다이나믹스 |
|---|
 |
궤도역학에서 호만 전이 궤도(//ˈhomən/)는 때때로 양쪽 모두에 접선되는 동일한 평면에서 중심체를 중심으로 서로 다른 반지름의 두 개의 원형 궤도 사이를 이동하는데 사용되는 타원형 궤도다.Hohmann transfer는 종종 이러한 궤도를 이동할 때 가능한 가장 낮은 양의 추진제를 사용하지만, 경우에 따라 생물-엘리틱 전송은 덜 사용할 수 있다.
호만 트랜스퍼를 수행하기 위한 궤도 기동은 두 개의 프로그램 엔진 임펄스를 사용한다. 하나는 우주선을 전송 궤도로 이동시키기 위한 것이고 다른 하나는 우주선을 이동시키기 위한 것이다.이 기동은 독일 과학자 월터 호만(Walter Hohmann)이 1925년 저서 《Die Erreichbarkeit der Himelskörper(천체의 달성 가능성)》에서 그에 대한 설명을 발표한 데서 이름을 따왔다.[1]호만은 독일 공상과학소설 작가 쿠르드 라스비츠와 1897년 저서 '두 행성'의 영향을 일부 받았다.
다른 신체들 사이의 타원형 전달 궤도(행성, 달 등)는 흔히 호만 전달 궤도라고 한다.천체 간 이동에 사용될 때, Hohmann 전달 궤도는 출발점과 목적지 지점이 서로 상대적인 궤도의 특정 위치에 있어야 한다.Hohmann 트랜스퍼를 사용하는 우주 미션은 소위 발사 창을 여는 이 필요한 정렬이 일어나기를 기다려야 한다.예를 들어, 지구와 화성 사이의 우주 임무를 위해, 이 발사 창문은 26개월마다 발생한다.또한 Hohmann 전송 궤도는 출발지와 목적지 사이를 이동하는 데 필요한 고정 시간을 결정한다. 지구-마스 여행의 경우 이 이동 시간은 약 9개월이다.중력이 큰 천체에 가까운 궤도를 이동할 경우 화상에 Oberth 효과를 사용할 수 있으므로 일반적으로 델타-v가 훨씬 적게 필요하다.
이러한 상황에도 자주 사용되지만 실제 엔진의 추력 한계를 고려한 저에너지 전달과 두 행성의 중력 웰의 활용이 더 연료 효율적일 수 있다.[2][3][4]
설명
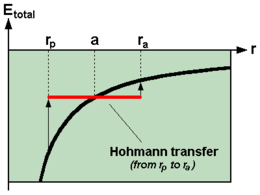
이 도표는 낮은 원형 궤도에서 더 높은 궤도로 우주선을 가져오기 위한 호만 트랜스퍼 궤도를 보여준다.우주선이 떠나고자 하는 하단 원형 궤도(도표에는 녹색으로, 도표에는 1로 표기)와 도달하고자 하는 고원형 궤도(도표에는 빨간색, 도표에는 3으로 표기)에 모두 닿는 타원형 궤도의 절반이다.전송(노란색 및 다이어그램에 2라는 라벨이 붙어 있음)은 우주선의 엔진을 발사하여 타원 궤도를 따라갈 수 있도록 가속함으로써 시작된다.이것은 우주선의 궤도에 에너지를 더한다.우주선이 목적지 궤도에 도달했을 때, 타원 궤도를 더 큰 원형 궤도로 바꾸려면 궤도 속도(따라서 궤도 에너지)를 다시 증가시켜야 한다.
궤도의 가역성 때문에, 호만 트랜스퍼 궤도는 또한 더 높은 궤도에서 더 낮은 궤도로 우주선을 끌어내는 작용을 한다. 이 경우, 우주선의 엔진은 현재의 경로와 반대 방향으로 발사되어 우주선의 속도를 늦추고 낮은 에너지의 타원형 트랜스퍼 궤도에 떨어지게 된다.그런 다음 엔진은 낮은 거리에서 다시 발사되어 우주선을 낮은 원형 궤도로 천천히 진입시킨다.
Hohmann 전달 궤도는 두 개의 순간 속도 변화에 기초한다.버스트에 시간이 걸린다는 사실을 보상하기 위해 여분의 연료가 필요하다. 이는 버스트의 지속시간을 최소화하기 위해 고러스트 엔진을 사용함으로써 최소화된다.지구 궤도에서의 이동의 경우, 두 개의 화상은 피리 화상과 아포기 화상으로[5] 표시된다(또는 "피오기 킥"). 더 일반적으로는 피리 화상과 아포피 화상으로 표시된다.또는 궤도를 순환시키기 위한 두 번째 화상은 원형화 화상으로 언급할 수 있다.
1종과 2종
이상적인 Hohmann 전달 궤도는 동일한 평면에서 두 개의 원형 궤도 사이를 이동하며 1차 궤도를 정확히 180° 돈다.실제 세계에서는 목적지 궤도가 원형 궤도가 아닐 수도 있고, 초기 궤도와 동일 평면 궤도가 아닐 수도 있다.실제 세계 이동 궤도는 1차 주위에서 180°보다 약간 더 많이 또는 약간 적게 횡단할 수 있다.1차 주위로 180° 미만을 가로지르는 궤도를 '타입 I' 호만 전이, 180° 이상을 가로지르는 궤도를 '타입 II' 호만 전이이라고 한다.[6][7]
이동 궤도는 태양 주위를 360° 이상 돌 수 있다.이러한 다중혁명전달을 타입 III 및 타입 IV라고 부르기도 하는데, 여기서 타입 III는 타입 I + 360°이고, 타입 IV는 타입 II + 360°[8]이다.
사용하다
Hohmann 전달 궤도는 물체의 궤도를 다른 물체로 이동하는데 사용될 수 있다. 물체가 궤도를 도는 공통의 큰 몸체를 공유하는 한 말이다.지구와 태양계의 맥락에서, 이것은 태양의 궤도를 도는 물체를 포함한다.Hohmann 전이 궤도를 사용할 수 있는 예로는 태양을 공전하는 소행성을 지구와 접촉시키는 것이다.[9]
계산
지구를 선회하는 위성처럼 훨씬 더 큰 몸체를 돌고 있는 작은 몸체의 경우, 작은 몸체의 총 에너지는 운동 에너지와 잠재적 에너지의 합이며, 이 총 에너지는 평균 a 반주축):
속도에 대한 이 방정식을 풀면 vis-viva 방정식이 된다.
- 은(는) 선회하는 차체의 속도,
- = 이가) M+ m 보다 유의하게 크지 않다고 가정하는 일차 본체의 표준 중력 매개변수( Mμ+m v v (지구상 이것은 μ~3.986E14 ms3−2)
- 은(는) 1차 초점으로부터 선회하는 차체의 거리,
- 는 신체의 궤도의 반주축이다.
따라서, Hohmann 전송에 필요한 델타-v(Δv)는 순간 자극을 가정하여 다음과 같이 계산할 수 있다.
케플러의 제3법칙에 의해 더 높은 궤도로 이동하든, 더 낮은 궤도로 이동하든, 궤도를 오가는 데 걸리는 시간은 다음과 같다.
한 천체에서 다른 천체로의 이동에 적용하기 위해서는 두 신체가 적절하게 정렬된 시점에 기동을 시작하는 것이 중요하다.목표 각속도를 고려하여
예
r1 = 6,678km(고도 300km)에서 시작하여 r2 = 42,164km(고도 35,786km)로 정지궤도로 끝나는 정지궤도를 고려한다.
더 작은 원형 궤도에서는 속도가 7.73km/s이고, 더 큰 궤도에서는 3.07km/s이다.속도 사이의 타원 궤도에서는 피리계의 10.15 km/s에서 아포기의 1.61 km/s까지 변화한다.
따라서 첫 번째 화상의 Δv는 10.15 - 7.73 = 2.42 km/s이고, 두 번째 화상의 Δv는 3.07 - 1.61 = 1.46 km/s이며, 두 화상의 Δv는 모두 3.88 km/s이다.
이것은 탈출 궤도에 필요한 Δv보다 크다: 10.93 - 7.73 = 3.20 km/s.0.78km/s(3.20-2.42)만 더 많은 저지구 궤도(LEO)에서 Δv를 적용하면 로켓은 지구동기 궤도를 원형화하는 데 필요한 1.46km/s의 Δv보다 적은 탈출 속도를 얻을 수 있다.이는 큰 속도에서 동일한 Δv가 보다 구체적인 궤도 에너지를 제공하고, Δv를 가능한 한 빨리 소비하여 중력에 의해 감속된 다음 감속을 극복하기 위해 더 많이 소비하면 에너지 증가가 극대화된다는 Oberth 효과를 보여준다(물론, Hohmann transfer o의 목적).rbit은 다르다).
최악의 경우, 최대 델타-V
위의 예에서 알 수 있듯이, 두 개의 원형 궤도 사이에서 호만 이전을 수행하는 데 필요한 Δv는 목적지 반경이 무한할 때 가장 크지 않다.(탈출 속도는 궤도 속도의 2배 Δv이므로 탈출에 필요한 Δv는 궤도 속도의 2 - 1(41.4%)이다.)더 큰 궤도의 반경이 15.5817일 때 필요한 Δv는 가장 크다(더 작은 궤도 속도의 53.0%).작은 궤도의 곱하기.[10]This number is the positive root of x3 − 15x2 − 9x − 1 = 0, which is . For higher orbit ratios the Δv required for the second burn decreases faster than the first increases.
행성간 여행에 대한 응용
우주선을 한 행성의 궤도를 선회하는 것에서 다른 행성의 궤도를 선회하는 데 사용할 때, 상황은 다소 복잡해지지만, 오베르트의 효과로 인해, 첫 번째 행성을 탈출하는 데 필요한 델타-V의 합과 두 번째 행성으로의 호만 이주에 필요한 델타-V의 합보다 훨씬 적은 델타-V가 필요하다.
예를 들어, 지구에서 화성으로 이동하는 우주선을 생각해 보자.여행이 시작될 때, 우주선은 이미 지구 궤도와 관련된 특정한 속도와 운동에너지를 갖게 될 것이다.연소 중에 로켓 엔진은 델타-v를 적용하지만, 운동 에너지는 행성의 중력 전위를 탈출하기에 충분할 때까지 사각형 법칙으로 증가하며, 그리고 나서 호만 트랜스퍼 궤도(태양 주변)에 들어갈 수 있는 충분한 에너지를 얻기 위해 더 많이 연소한다.로켓엔진은 추진체의 초기 운동에너지를 활용할 수 있기 때문에 탈출속도에 도달하는 데 필요한 델타-v 이상의 델타-v가 훨씬 적게 필요하며, 최적의 상황은 지구 위 최소고도(낮은 주탑스)에서 이송 화상이 이루어지는 경우다.우주선이 화성으로 향할 때 지구보다 2.9km/s 더 빨리 달릴 수 있음에도 불구하고, 필요한 델타-v는 3.6km/s에 불과해 지구를 탈출하는 데 필요한 것보다 약 0.4km/s 더 많을 뿐이다(아래 표 참조).
다른 쪽 끝에서, 우주선은 화성의 궤도를 돌기 위해 일정한 속도가 필요할 것이다. 화성과 같은 궤도에서 태양 궤도를 돌려는 것은 말할 것도 없고, 실제로 화성의 궤도를 계속 돌기 위해 필요한 속도보다 적을 것이다.따라서 화성의 중력이 화성을 사로잡기 위해서는 우주선이 감속해야 할 것이다.이 포획 화상은 Oberth 효과를 최적으로 활용하기 위해 낮은 고도에서 최적으로 수행되어야 한다.따라서 자유 공간 상황에 비해 전송을 주선하기 위해서는 여행의 양쪽 끝에서 비교적 적은 양의 추진력이 필요하다.
그러나, 어떤 호만 이전을 할 때, 두 행성의 궤도에 있는 정렬은 매우 중요하다. 목적지 행성과 우주선은 동시에 태양 주위를 도는 각각의 궤도에서 같은 지점에 도착해야 한다.이러한 정렬 요건은 발사 윈도우의 개념을 제기한다.
달 이동 궤도(LTO)라는 용어는 달에서 사용된다.
위에서 주어진 공식을 적용하여 지구로부터 다양한 목적지에 도착하기 위해 Hohmann 전달 궤도에 진입하는 데 필요한 Δv(km/s)를 계산할 수 있다(행성의 원형 궤도를 가정한다).이 표에서 "지구 궤도에서 호만 궤도로 진입하는 Δv"라고 표시된 기둥이 지구 속도에서 태양으로부터 원하는 거리에 있는 호만 타원에 오르는 데 필요한 속도에 변화를 준다."LEO에서 나가는 v"라는 라벨이 붙은 이 열은 지구 표면에서 300km 위에 있을 때 필요한 속도를 제공한다(지구를 중심으로 한 비회전 기준 프레임에서.이것은 특정 운동 에너지에 이 낮은 지구 궤도의 속도(7.73 km/s)의 제곱(즉, 이 LEO에서 지구의 중력의 깊이)을 더함으로써 얻어진다."LEO에서 Δv" 열은 단순히 이전 속도에서 7.73 km/s를 뺀 것이다.
| 목적지 | 궤도 반지름 (AU) | Δv (km/s) | ||
|---|---|---|---|---|
| 호만 궤도에 진입하다 지구 궤도에서 | 끝내는 레오 | 로부터 레오 | ||
| 태양 | 0 | 29.8 | 31.7 | 24.0 |
| 수성. | 0.39 | 7.5 | 13.3 | 5.5 |
| 금성 | 0.72 | 2.5 | 11.2 | 3.5 |
| 화성 | 1.52 | 2.9 | 11.3 | 3.6 |
| 목성 | 5.2 | 8.8 | 14.0 | 6.3 |
| 토성 | 9.54 | 10.3 | 15.0 | 7.3 |
| 천왕성 | 19.19 | 11.3 | 15.7 | 8.0 |
| 해왕성 | 30.07 | 11.7 | 16.0 | 8.2 |
| 명왕성 | 39.48 | 11.8 | 16.1 | 8.4 |
| Infinity | ∞ | 12.3 | 16.5 | 8.8 |
대부분의 경우 LEO의 Δv는 지구 궤도에서 호만 궤도로 진입하기 위한 Δv보다 작다는 점에 유의한다.
태양에 도달하기 위해서, 실제로 24 km/s의 Δv를 사용할 필요는 없다.8.8 km/s를 이용하여 태양으로부터 매우 멀리 떨어진 곳에 간 다음, 무시할 수 있는 Δv를 사용하여 각운동량을 0으로 만든 다음, 태양에 떨어질 수 있다.이는 1회 위아래로 두 번의 호만 전근으로 간주할 수 있다.또한 이 표에는 중력 보조를 위해 달을 사용할 때 적용되는 값이 나와 있지 않다.또한 다른 행성이나 태양으로의 이동을 돕기 위해 가장 쉽게 갈 수 있는 금성과 같은 하나의 행성을 사용할 가능성도 있다.
다른 이전과 비교
바이엘립트 전이
생물-엘리틱 전이(bi-elliptic transfer)는 두 개의 반엘리틱 궤도로 구성된다.초기 궤도로부터 첫 번째 화상은 델타-v를 팽창시켜 중심체로부터 어느 지점 r 에서 아포피스로 우주선을 첫 번째 전달 궤도로 끌어올린다.이 때 두 번째 화상은 우주선을 최종 원하는 궤도의 반지름에 페리옵시스(periapsis)가 있는 두 번째 타원궤도로 보내는데, 여기서 세 번째 화상이 행해져 원하는 궤도에 우주선을 주입한다.[11]
Hohmann 전송보다 엔진 화상이 한 번 더 필요하고 일반적으로 이동 시간이 더 많이 필요하지만, 일부 바이엘리틱 전송은 선택한 중간 반주축에 따라 최종 대 초기 반주축 비율이 11.94 이상일 때 Hohmann 전송보다 총 델타-v의 양이 더 적다.[12]
생물학적 이동 궤적에 대한 아이디어는 1934년 아리 스턴펠트에 의해 처음[citation needed] 출판되었다.[13]
저신뢰이전
저러스트 엔진은 조심스럽게 타이밍을 맞춘 엔진 발사를 통해 초기 원형 궤도를 점진적으로 확대함으로써 Hohmann 전달 궤도의 근사치를 수행할 수 있다.이를 위해서는 2-임펄스 전송궤도보다[14] 크고 완료하는 데 더 오랜 시간이 걸리는 속도 변화(델타-v)가 필요하다.
이온 추진기와 같은 엔진은 델타-v 모델로는 분석이 더 어렵다.이 엔진들은 매우 낮은 추진력과 동시에 훨씬 높은 델타-V 예산, 훨씬 더 높은 특정한 충동, 낮은 연료 질량과 엔진을 제공한다.2번 연소된 Hohmann 이송 기동은 그러한 낮은 추진력으로는 비실용적일 수 있다; 이 기동은 주로 연료 사용을 최적화하지만, 이 상황에서는 비교적 많은 연료가 있다.
만약 저-러스트 기술만 임무에 계획되어 있다면, 저-러스트 기술을 지속적으로 발사하지만, 매우 고효율 엔진은 더 높은 델타-V를 발생시킬 수 있고, 동시에 기존의 화학 로켓 엔진보다 추진제를 덜 사용할 수 있다.
반지름을 점진적으로 변화시킴으로써 한 원형 궤도에서 다른 원궤도로 가는 것은 단순히 두 속도 사이의 차이와 동일한 델타-v를 필요로 한다.[14]이러한 기동은 2번 탄 호만 전송 기법보다 델타-v가 더 많이 필요하지만, 높은 추력의 짧은 적용보다는 지속적으로 낮은 추력을 발휘한다.
사용된 추진제 질량의 양은 기동의 효율과 그것을 위해 사용되는 하드웨어를 측정한다.사용된 총 델타-v는 기동 효율만 측정한다.신뢰도가 낮은 경향이 있는 전기 추진계통의 경우, 추진계통의 높은 효율은 보통 보다 효율적인 호만 기동에 비해 높은 델타-V를 보상한다.
전기 추진력이나 저-러스트 엔진을 이용한 트랜스퍼 궤도는 Hohmann 트랜스퍼 궤도처럼 델타-v가 아닌 최종 궤도에 도달하기 위해 전송 시간을 최적화한다.정지궤도의 경우, 초기 궤도는 초동기식으로 설정되며, 아포지에서 속도 방향으로 연속적으로 추력함으로써 전달 궤도는 원형 지동기궤도로 변환한다.그러나 이 방법은 궤도에 주입된 낮은 추력 때문에 달성하는 데 훨씬 더 오랜 시간이 걸린다.[15]
행성간 교통망
1997년에, 행성간 교통 네트워크(ITN)라고 알려진 궤도를 발행하여, 호만 트랜스퍼 궤도에 비해 다른 궤도 사이에 추진력이 더 낮은 델타-V(더 느리고 더 길지만) 경로를 제공하였다.[16]행성간 전송 네트워크는 Hohmann 이체가 단지 하나의 큰 몸체만을 가정하는 반면 행성간 전송 네트워크는 그렇지 않기 때문에 Hohmann이 전송하는 것과는 성격이 다르다.행성간 교통 네트워크는 행성들의 중력 지원을 이용함으로써 덜 추진력 있는 델타-V의 사용을 달성할 수 있다.[citation needed]
참고 항목
인용구
- ^ Walter Hohmann, The Attractability of Heaven Bodys (워싱턴: NASA Technical Translation F-44, 1960) 인터넷 아카이브.
- ^ Williams, Matt (2014-12-26). "Making the Trip to Mars Cheaper and Easier: The Case for Ballistic Capture". Universe Today. Retrieved 2019-07-29.
- ^ Hadhazy, Adam. "A New Way to Reach Mars Safely, Anytime and on the Cheap". Scientific American. Retrieved 2019-07-29.
- ^ "An Introduction to Beresheet and Its Trajectory to the Moon". Gereshes. 2019-04-08. Retrieved 2019-07-29.
- ^ 조나단 맥도웰, "Kick In the Apoge: 40년 동안 고체 로켓 모터의 상위 단계 적용, 1957-1997년", 제33회 AIAA 공동 추진 회의, 1997년 7월 4일. 추상적.2017년 7월 18일 회수
- ^ NASA, 우주 비행의 기본, 제1장 제4장 "트래젝토리"2017년 7월 26일 회수spaceodyssey.dmns.org도 이용 가능하다.
- ^ 타이슨 스파크스, 2012년 12월 14일 콜로라도 Astrodynamics Research의 화성행 궤도.2017년 7월 25일 회수.
- ^ Langevin, Y. (2005)"우주 과학 미션의 설계 이슈," V. Martnez Pillet, A. 우주 과학의 페이로드와 미션 정의.아파리치오, 그리고 F.산체스, 에드, 캠브리지 대학 출판부, 30페이지ISBN 052185802X, 9780521858021
- ^ Calla, Pablo; Fries, Dan; Welch, Chris (2018). "Asteroid mining with small spacecraft and its economic feasibility" (PDF). arXiv:1808.05099.
- ^ Vallado, David Anthony (2001). Fundamentals of Astrodynamics and Applications. Springer. p. 317. ISBN 0-7923-6903-3.
- ^ Curtis, Howard (2005). Orbital Mechanics for Engineering Students. Elsevier. p. 264. ISBN 0-7506-6169-0.
- ^ Vallado, David Anthony (2001). Fundamentals of Astrodynamics and Applications. Springer. p. 318. ISBN 0-7923-6903-3.
- ^ Sternfeld, Ary J.[원문대로](1934-02-12),"d'approcherd'un 군단d'une orbite keplérienne partir 중앙 à attractif 수르도permettant trajectoires donnée"[허용된 궤적이 주어진 케플러 궤도로부터 중심 매력적인 몸에 접근한 연구], Comptes rendus 드 l'Académie 데 과학(프랑스어로), 파리, 198(1):711–713{{표창}}:C.S1maint:추가 문장 부호(링크).
- ^ a b MIT, 16.522: 우주 추진, 세션 6, 2015년 봄(2017년 7월 26일 회수)
- ^ Spitzer, Arnon (1997). Optimal Transfer Orbit Trajectory using Electric Propulsion. USPTO.
- ^ Lo, M. W.; Ross, S. D. (1997). "Surfing the Solar System: Invariant Manifolds and the Dynamics of the Solar System". Technical Report. IOM. JPL. pp. 2–4. 312/97.
일반 출처
- Walter Hohmann (1925). Die Erreichbarkeit der Himmelskörper. Verlag Oldenbourg in München. ISBN 3-486-23106-5.
- Thornton, Stephen T.; Marion, Jerry B. (2003). Classical Dynamics of Particles and Systems (5th ed.). Brooks Cole. ISBN 0-534-40896-6.
- Bate, R.R.; Mueller, D.D.; White, J.E. (1971). Fundamentals of Astrodynamics. Dover Publications, New York. ISBN 978-0-486-60061-1.
- Vallado, D. A. (2001). Fundamentals of Astrodynamics and Applications (2nd ed.). Springer. ISBN 978-0-7923-6903-5.
- Battin, R.H. (1999). An Introduction to the Mathematics and Methods of Astrodynamics. American Institute of Aeronautics & Ast, Washington, DC. ISBN 978-1-56347-342-5.
추가 읽기
- "Orbital Mechanics". Rocket and Space Technology. Robert A. Braeunig. Archived from the original on 2012-02-04. Retrieved 2005-08-17.
- "4. Interplanetary Trajectories". Basics of Spaceflight. JPL: NASA.






 (는) 선회하는 차체의 속도,
(는) 선회하는 차체의 속도,



 (는) 1차 초점으로부터 선회하는 차체의 거리,
(는) 1차 초점으로부터 선회하는 차체의 거리,












 두 번째
두 번째 



