플럭스
Flux
플럭스는 표면 또는 물질을 통과하거나 이동하는 것으로 보이는 효과를 나타냅니다(실제로 이동하는지 여부에 관계없이).플럭스는 응용 수학과 벡터 미적분학의 개념으로 물리학에 많은 응용을 가지고 있다.수송 현상의 경우, 플럭스는 물질 또는 성질의 흐름의 크기와 방향을 나타내는 벡터량입니다.벡터 미적분학에서 플럭스는 스칼라량으로,[1] 벡터장의 수직 성분의 표면 적분으로 정의됩니다.
용어.
플럭스라는 단어는 라틴어에서 왔다: 플럭수스는 "흐름"을 의미하고, 연도(flue)는 "흐름"[2]을 의미한다.플럭션으로서, 이 용어는 아이작 뉴턴에 의해 미적분에 도입되었습니다.
열 플럭스의 개념은 조셉 푸리에의 열 전달 [3]현상 분석에서 핵심적인 기여를 했습니다.그의 독창적인 논문 Théorie 때로는 드 라chaleur(Analytical이론의)[4]드 중심적인 것으로 되고, 판석을 가로질러 온도 차이의 측면에서 그리고 좀 더 일반적으로 온도의 다른 geome을 가로질러 온도 구배나 격차 관점에서 유량의 잘 알려 진 표현을 유도하기 위해 유동을 정의합니다.tr그렇다.[5] 누군가는 James Cluck Maxwell의 연구에 근거해, 운송의 정의가 전자기학에 사용되는 플럭스의 정의보다 우선한다고 주장할 수 있다.Maxwell의 구체적인 인용문은 다음과 같습니다.
플럭스의 경우 플럭스의 적분을 표면의 모든 요소를 통과시켜야 합니다.이 연산의 결과를 플럭스의 표면 적분이라고 합니다.그것은 표면을 통과하는 양을 나타냅니다.
--
수송 정의에 따르면 플럭스는 단일 벡터일 수도 있고 벡터장/위치함수일 수도 있다.후자의 경우 플럭스는 표면에 쉽게 통합될 수 있다.반면, 전자석 정의에 따르면 플럭스는 표면상의 적분입니다. 즉, 2차 정의 플럭스를 적분하는 것은 표면상의 적분이 두 번 되는 것은 의미가 없습니다.따라서 Maxwell의 인용은 "flux"가 전송 정의에 따라 사용되는 경우에만 의미가 있습니다(또한 단일 벡터가 아닌 벡터 필드입니다).맥스웰은 전자기학의 정의에 따르면 우리가 현재 "전기 플럭스"와 "자기 플럭스"라고 부르는 것의 주요 개발자 중 하나였기 때문에 이것은 아이러니하다.인용(및 운송 정의)에 따른 이름은 "전기 플럭스의 표면 적분" 및 "자기 플럭스의 표면 적분"이며, 이 경우 "전기 플럭스"는 "전기 플럭스"로 정의되고 "자기 플럭스"는 "자기장"으로 정의됩니다.이는 Maxwell이 이러한 필드를 일종의 흐름/플루스로 생각했음을 의미합니다.
전자석 정의에 따른 플럭스가 주어졌을 때 해당 플럭스 밀도는 해당 용어가 사용되는 경우 통합된 표면을 따른 해당 플럭스 밀도를 나타냅니다.미적분의 기본정리에 따르면, 대응하는 플럭스밀도는 수송정의에 따른 플럭스이다.전류와 같은 전류(시간당 충전)가 주어질 경우, 전류 밀도 또한 전송 정의에 따라 면적당 시간당 충전량이 됩니다.플럭스의 상충되는 정의와 비기술적인 영어에서의 플럭스, 흐름 및 전류의 교환 가능성 때문에, 이 항에서 사용되는 모든 용어는 때때로 상호 교환 가능하고 모호하게 사용됩니다.이 문서의 나머지 부분에 있는 콘크리트 플럭스는 용어가 대응하는 플럭스의 정의에 관계없이 문헌에서 폭넓게 받아들여지고 있는 내용에 따라 사용됩니다.
단위 면적당 유량으로서의 플럭스
수송 현상(열 전달, 질량 전달 및 유체 역학)에서 플럭스는 단위 면적당 특성의 흐름 속도로 정의되며, 이는 치수[수량]를 갖는다.·[시간]−1 ·[지역]−1[6]속성이 "통과" 또는 "횡단"으로 흐르는 지표면 영역입니다.예를 들어, 강의 흐름의 크기, 즉 매초 강의 단면을 흐르는 물의 양 또는 매초 지면에 착지하는 햇빛 에너지의 양은 일종의 플럭스입니다.
일반적인 수학적 정의(수송)
다음은 복잡도 증가 순서에 대한 세 가지 정의입니다.각각 다음과 같은 특수한 경우입니다.모든 경우에 빈번한 기호 j(또는 J)는 플럭스, q는 흐르는 물리량, t는 시간, A는 면적에 사용됩니다.이러한 식별자는 벡터일 때만 굵은 글씨로 표시됩니다.
첫째, (단일) 스칼라로서의 플럭스:
둘째, 표면을 따라 정의된 스칼라 장으로서의 플럭스, 즉 표면의 점 함수:
마지막으로, 벡터 장으로서의 플럭스:
특성.
이러한 직접적인 정의, 특히 마지막 정의는 다소 다루기 어렵다.예를 들어 아르그맥스 구조는 웨더베인 등을 사용하면 한 지점에서 플럭스의 방향을 쉽게 추론할 수 있을 때 경험적 측정의 관점에서 인위적이다.벡터 플럭스를 직접 정의하는 것보다 벡터 플럭스에 대한 몇 가지 특성을 설명하는 것이 더 직관적인 경우가 많습니다.게다가 이러한 성질로부터, 어쨌든 플럭스를 일의로 결정할 수 있다.
플럭스 j가 영역을 θ 각도로 통과하여 영역까지 도달하는 경우,
벡터 플럭스는 표면 S 위의 j의 표면 적분이 표면을 통과하는 시간 단위당 적절한 흐름을 제공한다.
마지막으로 t에서 t까지의 시간에12 걸쳐 다시 적분하여 해당 시간(t2 - t1) 동안 표면을 흐르는 성질의 총량을 얻을 수 있습니다.
수송 플럭스
운송 현상 문헌에서 가장 일반적인 형태의 플럭스는 다음과 같이 정의된다.
- 운동량 플럭스, 단위 면적 전체의 운동량 전달 속도(N·s·m−2·s−1).(뉴턴의 [7]점도의 법칙)
- 열유속, 단위 면적에 걸친 열유동 속도(J·m−1·s−2).(Fourier의 [8]전도 법칙)(이 열 플럭스의 정의는 Maxwell의 원래 정의에 부합합니다.)[5]
- 확산 플럭스, 단위 면적 전체에 걸친 분자의 이동 속도−1(mol·m−2·s).(Fick'[7]s 확산의 법칙)
- 체적 플럭스, 단위 면적에 걸친 체적 흐름 속도(m3·m−2·s−1) (다아시의 지하수 흐름 법칙)
- 질량 플럭스, 단위 면적에 걸친 질량 흐름 속도(kg·m−2·s−1).(분자 질량을 포함하는 픽의 법칙의 대체 형태 또는 밀도를 포함하는 다아시의 법칙의 대체 형태 중 하나)
- 방사 플럭스, 단위 면적당 선원에서 특정 거리/초(J·m−2·s−1)에서 광자의 형태로 전달되는 에너지의 양.천문학에서 별의 크기와 스펙트럼 등급을 결정하는 데 사용됩니다.또한 전자파 스펙트럼으로 제한될 경우 방사 플럭스와 동일한 열 플럭스의 일반화 역할을 합니다.
- 에너지 플럭스, 단위 면적을 통한 에너지 전달 속도(J·m−2·s−1).방사 플럭스와 열 플럭스는 에너지 플럭스의 특정 사례입니다.
- 입자속, 단위면적에서의 입자전달속도([입자수] m−2·s−1)
이러한 플럭스는 공간의 각 지점에서 벡터이며 일정한 크기와 방향을 가지고 있습니다.또, 이러한 플럭스의 편차를 취해, 공간의 소정점 주위의 제어 부피내의 양의 축적 속도를 결정할 수 있다.압축할 수 없는 흐름의 경우 부피 플럭스의 분산은 0입니다.
화학 확산
위에서 언급한 바와 같이 등온 등압 시스템에서 성분 A의 화학적 몰 플럭스는 Fick의 확산 법칙에서 다음과 같이 정의된다.
이 플럭스는 mol·m−2·s−1 단위를 가지며 Maxwell의 [5]플럭스에 대한 원래 정의에 부합합니다.
희박한 가스의 경우, 운동 분자 이론은 확산 계수 D를 입자 밀도 n = N/V, 분자 질량 m, 충돌 단면 {\ 및 절대 온도 T와 다음과 같이 관련짓습니다.
난류에서 와동운동에 의한 수송은 대폭 증가한 확산계수로 표현될 수 있다.
양자역학
양자역학에서, 양자 상태 θ(r, t)에 있는 질량 m의 입자는 다음과 같이 정의된 확률 밀도를 가진다.
표면 적분으로서의 플럭스
일반적인 수학적 정의(표면 적분)
수학적인 개념으로서 플럭스는 벡터장의 [12]표면 적분으로 표현된다.
여기서 F는 벡터장, dA는 표면 법선으로 향하는 표면 A의 벡터 영역입니다.두 번째, n은 표면에 대한 바깥쪽 뾰족한 단위 법선 벡터이다.
표면은 방향을 결정할 수 있어야 합니다. 즉, 두 면을 구분할 수 있습니다. 즉, 표면이 다시 접히지 않습니다.또한 표면은 실제로 방향을 향해야 합니다. 즉, 어느 방향으로 흐르느냐에 대한 규칙을 사용하고, 그 후 역흐름을 음으로 카운트합니다.
표면 법선은 보통 오른손 법칙에 의해 지시됩니다.
반대로 플럭스를 보다 기본적인 양으로 간주할 수 있으며 벡터장을 플럭스 밀도라고 부릅니다.
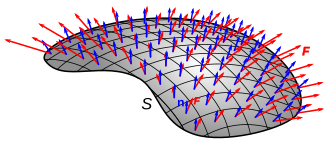
벡터장은 종종 "흐름" 다음에 이어지는 곡선(필드 라인)에 의해 그려집니다. 벡터장의 크기는 선 밀도이고 표면을 통과하는 플럭스는 선 수입니다.선은 양의 발산(소스) 영역에서 시작하여 음의 발산(싱크) 영역에서 끝납니다.
오른쪽의 그림도 참조해 주세요.단위 영역을 통과하는 붉은 화살표는 플럭스 밀도이며, 빨간색 화살표는 표면의 경계를 나타내며, 화살표의 표면 방향은 벡터 필드의 내부곱의 표면 규범 부호를 나타냅니다.
표면이 3D 영역을 둘러싸는 경우, 일반적으로 유입이 양으로 계산되도록 표면이 방향을 잡습니다. 그 반대는 아웃플룩스입니다.
발산정리는 닫힌 표면을 통한 순유출, 다시 말해 3D 영역의 순유출은 영역의 각 지점에서 국소 순유출(분산으로 표현됨)을 더함으로써 발견된다고 기술한다.
표면이 닫히지 않으면 방향 곡선을 경계로 한다.스토크스의 정리는 벡터장의 컬 플럭스가 이 경계를 넘어 벡터장의 선 적분이라고 말한다.이 경로 적분은 특히 유체 역학에서 순환이라고도 합니다.따라서 컬은 순환 밀도입니다.
플럭스와 이 이론들을 영역을 통해 전류, 힘 등이 적용되는 많은 분야에 적용할 수 있습니다.
전자기학
전자기에서 플럭스의 개념을 더 잘 이해하는 한 가지 방법은 그것을 나비 그물에 비교하는 것이다.그물망을 통과하는 공기의 양은 플럭스입니다.풍속이 높으면 그물을 통과하는 플럭스가 커집니다.그물이 커지면 풍속이 같아도 플럭스는 커진다.대부분의 공기가 그물을 통과하기 위해서는 그물의 개구부가 바람이 부는 방향을 향해야 합니다.그물이 바람과 평행하면 바람은 그물을 통과하지 못할 것이다.플럭스를 생각하는 가장 간단한 방법은 "그물을 통과하는 공기의 양"입니다. 여기서 공기는 속도장이고 그물은 가상의 표면의 경계입니다.
전기 플럭스
우주의 단일 양성자와 같은 전기 "전하"는 쿨롬으로 정의된 크기를 가집니다.이러한 전하에는 주위에 전장이 감겨 있습니다.그림 형태로, 양점 전하로부터의 전계는 전계선을 방사하는 점(때로는 "힘선"이라고도 함)으로 시각화할 수 있습니다.개념적으로, 전기 플럭스는 주어진 영역을 통과하는 "전계선 수"로 생각할 수 있습니다.수학적으로, 전기 플럭스는 주어진 영역에 걸친 전기장의 정상 구성요소의 적분입니다.따라서 MKS 시스템에서 전류의 단위는 newtons per coolon x m2 또는 N m2/C이다(전류 밀도는 단위 면적당 전류의 정상 성분의 강도에 대한 측정값).단위는 N/C로 MKS 단위의 전장과 동일합니다.)
두 가지 형태의 전기 플럭스가 사용됩니다. 하나는 [13][14]E-장용입니다.
및 D 필드용(전기 변위라고 함):
이 양은 가우스의 법칙에서 발생합니다. 닫힌 표면에서 나오는 전계 E의 플럭스는 표면에 포함된 전하A Q에 비례하며(전하가 분포되는 방식과 무관함), 적분 형태는 다음과 같습니다.
여기서 θ는0 여유 공간의 유전율입니다.
전계벡터 E의 전계벡터 E의 유속을 전계에 접하는 선으로 형성되어 있는 전하를 포함하지 않는 관에 대해 전계벡터 E의 유속을 고려할 때 측 플럭스는 0이 되어 관의 양단에 등반 플럭스가 있다.이것은 가우스의 법칙이 역제곱 필드에 적용된 결과이다.튜브의 단면에 대한 플럭스는 동일합니다.전하 q를 둘러싼 모든 표면의 총 플럭스는 q0/[15]µ입니다.
자유 공간에서 전기 변위는 구성 관계 D = δ0 E로 주어지며, 따라서 경계 표면에서 D-장 플럭스는 그 내부의 전하A Q와 같다.여기서 "flux of"라는 표현은 수학적 연산을 나타내며, 실제로 전계선을 따라 흐르는 것이 없기 때문에 볼 수 있듯이 결과가 반드시 "흐름"일 필요는 없다.
자속
단위 Wb/m2(Tesla)의 자속밀도(자기장)는 B로 나타내며, 자속은 다음과 [13][14]같이 정의한다.
위의 표기와 같은 표기로.이 양은 패러데이의 유도 법칙에서 발생하는데, 여기서 자속은 경계가 시간에 의존하거나 자기장이 시간에 의존하기 때문에 시간에 의존합니다.통합형식:
여기서 d is는 닫힌 곡선의 극소 벡터 선 요소A {\ A이며, 크기는 극소 선 요소의 길이와 같으며 곡선A {\ \ A}에 접선하여 주어진 방향이며, 부호는 적분 방향에 따라 결정됩니다.
와이어 루프를 통한 자속 변화 속도는 와이어에서 생성되는 기전력을 뺀 값입니다.이 방향은 전류가 와이어를 통과하도록 허용하면 기전력이 전류를 발생시켜 자기장의 변화를 "반대"하게 하여 변경과 반대되는 자기장을 생성하도록 합니다.이것은 인덕터와 많은 발전기의 기초이다.
포인팅 플럭스
이 정의를 사용하면 특정 표면에 걸친 포인팅 벡터 S의 플럭스는 전자파 에너지가 해당 표면을 통과하는 속도이며,[14] 이는 다음과 같이 정의된다.
표면을 통과하는 포인팅 벡터의 플럭스는 표면을 통과하는 전자기력 또는 단위시간당 에너지입니다.이는 일반적으로 전자기 방사 분석에서 사용되지만 다른 전자기 시스템에도 적용된다.
혼란스럽지만, 포인팅 벡터는 때때로 파워 플럭스라고 불리기도 하는데,[16] 이것은 위의 플럭스의 첫 번째 사용의 예입니다.그것은 평방미터당 와트(W/m2)의 단위를 가지고 있다.
SI 방사선 측정 단위
| 양 | 구성 단위 | 치수 | 메모들 | |||||
|---|---|---|---|---|---|---|---|---|
| 이름. | 기호.[nb 1] | 이름. | 기호. | 기호. | ||||
| 복사 에너지 | Qe[nb 2] | 줄 | J | MlLtT2−2 | 전자기 방사 에너지 | |||
| 복사 에너지 밀도 | we | 입방미터당 줄 | J/M3 | MlLtT−1−2 | 단위 볼륨당 복사 에너지. | |||
| 복사 플럭스 | Φe[nb 2] | 와트 | W = J/s | MlLtT2−3 | 단위 시간당 방출, 반사, 송신 또는 수신된 복사 에너지.이것은 때때로 "방사능력"이라고도 불리며 천문학에서는 광도라고 불립니다. | |||
| 스펙트럼 플럭스 | Φe,ν[nb 3] | 와트/헤르츠 | W/Hz | MlLtT2−2 | 단위 주파수 또는 파장당 복사 플럭스.후자는 일반적으로 Wµnm−1 단위로 측정됩니다. | |||
| Φe,λ[nb 4] | 미터당 와트 | W/m | MlLtT−3 | |||||
| 복사 강도 | Ie, δ[nb 5] | 스테라디안당 와트 | W/sr | MlLtT2−3 | 단위 고체 각도당 방출, 반사, 송신 또는 수신된 복사 플럭스.이것은 방향수량입니다. | |||
| 스펙트럼 강도 | Ie, ω, e[nb 3] | 스테라디안당 와트/헤르츠 | WµsrµHz−1−1 | MlLtT2−2 | 단위 주파수 또는 파장당 복사 강도.후자는 일반적으로 W'sr−1'nm−1 단위로 측정됩니다.이것은 방향수량입니다. | |||
| Ie, ω, e[nb 4] | 스테라디안 당 와트/미터 | W−1 wsrµm−1 | MlLtT−3 | |||||
| 광휘도 | Le, δ[nb 5] | 스테라디안당 평방미터당 와트 | W−1 wsrµm−2 | MtT−3 | 표면에 의해 방출, 반사, 투과 또는 수신되는 복사 플럭스(단위 투영 면적당 단위 고체 각도당).이것은 방향수량입니다.이것은 때때로 혼란스럽게 "강도"라고도 불립니다. | |||
| 스펙트럼 광도 | Le, ω, e[nb 3] | 스테라디안당 평방미터당 헤르츠당 와트 | WµsrµmµHz−1−2−1 | MtT−2 | 단위 주파수 또는 파장당 표면의 광도.후자는 일반적으로 W'sr−1'm−2'nm−1 단위로 측정됩니다.이것은 방향수량입니다.이것은 때때로 혼란스럽게 "스펙트럼 강도"라고도 불립니다. | |||
| Le, ω, e[nb 4] | 평방미터당 스테라디안당 와트, 미터당 | W−1 wsrµm−3 | MlLtT−1−3 | |||||
| 방사 조도 플럭스 밀도 | Ee[nb 2] | 평방미터당 와트 | W/m2 | MtT−3 | 단위 면적당 표면이 받는 복사 플럭스입니다.이것은 때때로 혼란스럽게 "강도"라고도 불립니다. | |||
| 스펙트럼 조사 강도 스펙트럼 플럭스 밀도 | Ee,120[nb 3] | 평방미터당 와트/헤르츠 | WµmµHz−2−1 | MtT−2 | 단위 주파수 또는 파장당 표면의 조사 강도.이것은 때때로 혼란스럽게 "스펙트럼 강도"라고도 불립니다.스펙트럼 플럭스 밀도의 비 SI 단위에는 얀스키(1 Jy = 10−26 WµmµHz−2−1)와 태양 플럭스 단위(1 sfu = 10−22 WµmµHz−2−1 = 104 Jy)가 포함된다. | |||
| Ee,120[nb 4] | 평방미터당 와트, 미터 당 와트 | W/m3 | MlLtT−1−3 | |||||
| 전파성 | Je[nb 2] | 평방미터당 와트 | W/m2 | MtT−3 | 단위 면적당 표면을 떠나는(방출, 반사 및 투과) 복사 플럭스.이것은 때때로 혼란스럽게 "강도"라고도 불립니다. | |||
| 스펙트럼 방사성 | Je,120[nb 3] | 평방미터당 와트/헤르츠 | WµmµHz−2−1 | MtT−2 | 단위 주파수 또는 파장당 표면의 방사선성.후자는 일반적으로 WΩnm−2−1 단위로 측정됩니다.이것은 때때로 혼란스럽게 "스펙트럼 강도"라고도 불립니다. | |||
| Je,120[nb 4] | 평방미터당 와트, 미터 당 와트 | W/m3 | MlLtT−1−3 | |||||
| 복사 출구 | Me[nb 2] | 평방미터당 와트 | W/m2 | MtT−3 | 단위 면적당 표면에 의해 방출되는 복사 플럭스.이것은 방사성의 성분입니다."방사성 방출"은 이 양을 나타내는 오래된 용어입니다.이것은 때때로 혼란스럽게 "강도"라고도 불립니다. | |||
| 스펙트럼 이탈 | Me,120[nb 3] | 평방미터당 와트/헤르츠 | WµmµHz−2−1 | MtT−2 | 단위 주파수 또는 파장당 표면의 복사 출구.후자는 일반적으로 WΩnm−2−1 단위로 측정됩니다."스펙트럼 방사량"은 이 양을 나타내는 오래된 용어입니다.이것은 때때로 혼란스럽게 "스펙트럼 강도"라고도 불립니다. | |||
| Me,120[nb 4] | 평방미터당 와트, 미터 당 와트 | W/m3 | MlLtT−1−3 | |||||
| 방사 노출 | He | 평방미터당 줄 | J/M2 | MtT−2 | 단위 면적당 표면이 받는 복사 에너지 또는 조사 시간에 걸쳐 통합된 표면의 등가 복사 강도.이것은 때때로 "방사성 플루언스"라고도 불립니다. | |||
| 스펙트럼 노출 | He,120[nb 3] | 평방미터/헤르츠당 줄 | ⋅mhzHz−2−1 | MtT−1 | 단위 주파수 또는 파장당 표면의 복사 노출.후자는 일반적으로 J'm−2'nm−1 단위로 측정됩니다.이것은 때때로 "스펙트럼 플루언스"라고도 불립니다. | |||
| He,120[nb 4] | 평방미터당 줄 | J/M3 | MlLtT−1−2 | |||||
| 반구 방사율 | ε | — | 1 | 표면과 같은 온도에서 흑체의 표면으로 나눈 표면의 복사 출구. | ||||
| 스펙트럼 반구 방사율 | εν 또는 ελ | — | 1 | 표면과 동일한 온도에서 흑체의 표면으로 나눈 표면의 스펙트럼 이탈. | ||||
| 방향 방사율 | εΩ | — | 1 | 표면에서 방출되는 광도를 해당 표면과 동일한 온도에서 흑체가 방출하는 광도로 나눈 값입니다. | ||||
| 스펙트럼 방향 방사율 | εω, ν 또는 εω, λ | — | 1 | 표면에서 방출되는 스펙트럼 광도를 해당 표면과 동일한 온도의 흑체 광도로 나눈 값입니다. | ||||
| 반구 흡수율 | A | — | 1 | 표면이 흡수하는 복사 플럭스로, 해당 표면이 받는 것으로 나눕니다.이것은 "흡수"와 혼동해서는 안 된다. | ||||
| 스펙트럼 반구 흡수율 | Aν 또는 Aλ | — | 1 | 표면이 흡수하는 스펙트럼 플럭스로, 해당 표면이 받는 것으로 나눕니다.이를 "스펙트럼 흡광도"와 혼동해서는 안 된다. | ||||
| 방향 흡광도 | AΩ | — | 1 | 표면에 흡수된 광도를 해당 표면에 입사한 광도로 나눈 값입니다.이것은 "흡수"와 혼동해서는 안 된다. | ||||
| 스펙트럼 방향 흡광도 | Aω, ν 또는 Aω, λ | — | 1 | 표면에 흡수된 스펙트럼 방사 광도를 해당 표면에 입사하는 스펙트럼 방사 광도로 나눈 값.이를 "스펙트럼 흡광도"와 혼동해서는 안 된다. | ||||
| 반구 반사율 | R | — | 1 | 표면에 반사된 복사 플럭스로, 해당 표면에 의해 수신된 것으로 나눕니다. | ||||
| 스펙트럼 반구 반사율 | Rν 또는 Rλ | — | 1 | 표면에 반사된 스펙트럼 플럭스로, 해당 표면에 의해 수신된 것으로 나눕니다. | ||||
| 방향 반사율 | RΩ | — | 1 | 표면에 반사된 광도를 해당 표면에 의해 수신된 광도로 나눈 값입니다. | ||||
| 스펙트럼 방향 반사율 | Rω, ν 또는 Rω, λ | — | 1 | 표면에서 반사된 스펙트럼 방사도를 해당 표면에서 수신한 것으로 나눈 값입니다. | ||||
| 반구 투과율 | T | — | 1 | 표면에 의해 전달되는 복사 플럭스로, 해당 표면에 의해 수신된 것으로 나눕니다. | ||||
| 스펙트럼 반구 투과율 | Tν 또는 Tλ | — | 1 | 표면에 의해 전달되는 스펙트럼 플럭스로, 해당 표면에 의해 수신된 것으로 나눕니다. | ||||
| 방향 투과율 | TΩ | — | 1 | 표면에 의해 전달되는 광도를 해당 표면에 의해 수신된 광도로 나눈 값입니다. | ||||
| 스펙트럼 방향 투과율 | Tω, ν 또는 Tω, λ | — | 1 | 표면에 의해 전달되는 스펙트럼 복사 강도를 해당 표면에 의해 수신된 것으로 나눈 값입니다. | ||||
| 반구 감쇠 계수 | μ | 역계 | 마−1 | L−1 | 단위 길이당 부피로 흡수 및 산란된 복사 플럭스를 해당 부피로 나눈 값입니다. | |||
| 스펙트럼 반구 감쇠 계수 | μν 또는 μλ | 역계 | 마−1 | L−1 | 흡수 및 산란된 스펙트럼 복사 플럭스를 단위 길이당 부피로 나눈 값. | |||
| 방향 감쇠 계수 | μΩ | 역계 | 마−1 | L−1 | 단위 길이당 볼륨으로 흡수 및 산란된 광도를 해당 볼륨으로 받은 광도로 나눈 값입니다. | |||
| 스펙트럼 방향 감쇠 계수 | μω, ν 또는 μω, λ | 역계 | 마−1 | L−1 | 단위 길이당 부피로 흡수 및 산란된 스펙트럼 방사 광도를 해당 부피로 받은 것으로 나눈 값. | |||
| 참고 항목: SI · 방사선 측정 · 측광 | ||||||||
- ^ 표준 기구들은 광도계량 또는 광자량과의 혼동을 피하기 위해 방사선량에는 접미사 "e"를 붙일 것을 권고한다.
- ^ a b c d e 때때로 나타나는 대체 기호: 복사 에너지의 경우 W 또는 E, 복사 플럭스의 경우 P 또는 F, 복사 조도의 경우 I, 복사 출구의 경우 W.
- ^ a b c d e f g 단위 주파수당 주어진 스펙트럼 양은 접미사 "θ"(그리스어)로 표시되며, 광도 측정량을 나타내는 접미사 "v"(시각적)와 혼동해서는 안 된다.
- ^ a b c d e f g 단위 파장당 주어진 스펙트럼 양은 접미사 "θ"(그리스어)로 표시됩니다.
- ^ a b 방향량은 접미사 "δ"(그리스어)로 표시됩니다.
「 」를 참조해 주세요.
메모들
- ^ 퍼셀, 페이지 22-26
- ^ Weekley, Ernest (1967). An Etymological Dictionary of Modern English. Courier Dover Publications. p. 581. ISBN 0-486-21873-2.
- ^ Herivel, John (1975). Joseph Fourier : the man and the physicist. Oxford: Clarendon Press. pp. 181–191. ISBN 0198581491.
- ^ Fourier, Joseph (1822). Théorie analytique de la chaleur (in French). Paris: Firmin Didot Père et Fils. OCLC 2688081.
- ^ a b c Maxwell, James Clerk (1892). Treatise on Electricity and Magnetism. ISBN 0-486-60636-8.
- ^ Bird, R. Byron; Stewart, Warren E.; Lightfoot, Edwin N. (1960). Transport Phenomena. Wiley. ISBN 0-471-07392-X.
- ^ a b P.M. Whelan; M.J. Hodgeson (1978). Essential Principles of Physics (2nd ed.). John Murray. ISBN 0-7195-3382-1.
- ^ Carslaw, H.S.; Jaeger, J.C. (1959). Conduction of Heat in Solids (Second ed.). Oxford University Press. ISBN 0-19-853303-9.
- ^ Welty; Wicks, Wilson and Rorrer (2001). Fundamentals of Momentum, Heat, and Mass Transfer (4th ed.). Wiley. ISBN 0-471-38149-7.
- ^ D. McMahon (2006). Quantum Mechanics Demystified. Demystified. Mc Graw Hill. ISBN 0-07-145546-9.
- ^ Sakurai, J. J. (1967). Advanced Quantum Mechanics. Addison Wesley. ISBN 0-201-06710-2.
- ^ M.R. Spiegel; S. Lipcshutz; D. Spellman (2009). Vector Analysis. Schaum's Outlines (2nd ed.). McGraw Hill. p. 100. ISBN 978-0-07-161545-7.
- ^ a b I.S. Grant; W.R. Phillips (2008). Electromagnetism. Manchester Physics (2nd ed.). John Wiley & Sons. ISBN 978-0-471-92712-9.
- ^ a b c D.J. Griffiths (2007). Introduction to Electrodynamics (3rd ed.). Pearson Education, Dorling Kindersley. ISBN 978-81-7758-293-2.
- ^ Feynman, Richard P (1964). The Feynman Lectures on Physics. Vol. II. Addison-Wesley. pp. 4–8, 9. ISBN 0-7382-0008-5.
- ^ Wangsness, Roald K. (1986). Electromagnetic Fields (2nd ed.). Wiley. ISBN 0-471-81186-6. 페이지 357
- Browne, Michael, PhD (2010). Physics for Engineering and Science, 2nd Edition. Schaum Outlines. New York, Toronto: McGraw-Hill Publishing. ISBN 978-0-0716-1399-6.
- Purcell, Edward, PhD (2013). Electricity and Magnetism, 3rd Edition. Cambridge, UK: Cambridge University Press. ISBN 978110-7014022.
추가 정보
- Stauffer, P.H. (2006). "Flux Flummoxed: A Proposal for Consistent Usage". Ground Water. 44 (2): 125–128. doi:10.1111/j.1745-6584.2006.00197.x. PMID 16556188. S2CID 21812226.
외부 링크
 Wiktionary에서 플럭스의 사전적 정의
Wiktionary에서 플럭스의 사전적 정의


 나눕니다. 각 패치를 통과하는 플럭스는 필드의 정상(수직) 성분인
나눕니다. 각 패치를 통과하는 플럭스는 필드의 정상(수직) 성분인
 D
D



































