등엔트로픽 과정
Isentropic process| 열역학 |
|---|
 |
열역학에서 등엔트로픽 과정은 단열적이면서도 [1][2][3][4][5][6]가역적인 이상적인 열역학 과정이다.시스템의 작업 전달은 마찰이 없으며 열이나 물질의 순 전달이 없습니다.이러한 이상적인 프로세스는 실제 [7]프로세스의 비교 모델 및 기준으로 엔지니어링에서 유용합니다.이것은 가역적 과정이 현실에서 일어나지 않기 때문에 이상화된다. 즉, 프로세스를 단열적 및 가역적으로 생각하는 것은 초기 엔트로피와 최종 엔트로피가 같다는 것을 보여주므로, 이 엔트로피는 변하지 않는다(엔트로피는 변하지 않는다).열역학적 과정은 시스템에 미치는 영향을 기준으로 명명됩니다(예: 이소볼루메트릭: 일정한 부피, 등온도픽: 일정한 엔탈피).실제로는 등엔트로픽 프로세스를 실행할 수 없는 경우도 있지만, 이와 같이 근사하는 경우도 있다.
"등변성"이라는 단어는 어원에서 추론할 수 있기 때문에 다른 방식으로 해석될 수 있다.이는 시스템의 엔트로피가 변하지 않는 프로세스를 의미합니다. 앞서 언급한 바와 같이 프로세스가 단열적이고 가역적인 경우 발생할 수 있습니다.단, 이는 시스템에 대한 작업이 시스템 내부의 마찰을 포함하고 내부 마찰을 보상하기 위해 적절한 양으로 시스템에서 열을 인출하여 엔트로피를 [8]변경하지 않는 시스템에서도 발생할 수 있다.하지만, 우주와 관련하여, 열역학 제2법칙에 따라 우주의 엔트로피가 증가하게 될 것이다.
배경
여기서 Q Q는 가열에 의해 시스템이 얻는 에너지량, 은 주변 온도, 는 엔트로피의 변화입니다.등호란 가역적인 과정을 말합니다.이것은 상상된 이상적인 이론적인 한계이며, 물리적 현실에서는 실제로 발생하지 않으며, 시스템과 [11][12]주변 환경의 온도가 근본적으로 동일합니다.등엔트로픽 프로세스의 경우, 가역적이더라도, 이 과정은 단열적이기 때문에 열과 같은 에너지 전달은 없다. δQ = 0이다.반대로 프로세스가 되돌릴 수 없는 경우에는 시스템 내에서 엔트로피가 생성되므로 시스템 내에서 엔트로피를 일정하게 유지하기 위해서는 열로서 시스템에서 에너지를 동시에 제거해야 합니다.
가역 프로세스의 경우 시스템을 주변으로부터 열적으로 "절연"함으로써 등엔트로픽 변환이 수행됩니다.온도는 엔트로피의 열역학적 켤레 변수입니다.따라서 켤레 과정은 시스템이 항온 열욕에 열적으로 "연결"되는 등온 과정입니다.
열역학 시스템의 등엔트로픽 과정
주어진 질량의 엔트로피는 내부적으로 가역적이고 단열적인 과정 동안 변하지 않습니다.엔트로피가 일정하게 유지되는 프로세스를 등방성 라고 으로 장치의 예로는 , 가스 압축기 터빈노즐 및 확산기 이 있습니다[13]
열역학 시스템에서 정상 흐름 장치의 등엔트로픽 효율성
대부분의 정상 흐름 디바이스는 단열 조건에서 작동하며, 이러한 디바이스의 이상적인 프로세스는 등엔트로픽 프로세스입니다.디바이스가 대응하는 등엔트로픽 디바이스에 얼마나 효율적으로 근접하는지를 나타내는 파라미터를 등엔트로픽 또는 단열 [13]효율이라고 부릅니다.
터빈의 등엔트로픽 효율:
압축기의 등엔트로픽 효율:
노즐의 등엔트로픽 효율:
위의 모든 공식에 대해:
- 1은 입구 상태의 특정 엔탈피입니다.
- 2 는 실제 프로세스의 출구 상태의 특정 엔탈피입니다.
- 는 등엔트로픽 프로세스의 출구 상태의 특정 엔탈피입니다.
열역학 사이클의 등엔트로픽 장치
| 사이클 | 등엔트로픽 단계 | 묘사 |
|---|---|---|
| 이상적인 랭킨 사이클 | 1→2 | 펌프 내 등엔트로픽 압축 |
| 이상적인 랭킨 사이클 | 3→4 | 터빈 내 등엔트로픽 팽창 |
| 이상적인 카르노 사이클 | 2→3 | 등엔트로픽 팽창 |
| 이상적인 카르노 사이클 | 4→1 | 등엔트로픽 압축 |
| 이상 오토 사이클 | 1→2 | 등엔트로픽 압축 |
| 이상 오토 사이클 | 3→4 | 등엔트로픽 팽창 |
| 이상적인 디젤 사이클 | 1→2 | 등엔트로픽 압축 |
| 이상적인 디젤 사이클 | 3→4 | 등엔트로픽 팽창 |
| 이상 브레이튼 사이클 | 1→2 | 압축기의 등엔트로픽 압축 |
| 이상 브레이튼 사이클 | 3→4 | 터빈 내 등엔트로픽 팽창 |
| 이상적인 증기 압축 냉동 사이클 | 1→2 | 압축기의 등엔트로픽 압축 |
| 이상 레누아르 순환 | 2→3 | 등엔트로픽 팽창 |
참고: 등엔트로픽 가정은 이상적인 사이클에서만 적용할 수 있습니다.실제 사이클에는 압축기와 터빈의 비효율성과 열역학 제2법칙으로 인한 손실이 내재되어 있습니다.실제 시스템은 진정한 등엔트로픽은 아니지만 등엔트로픽 거동은 많은 계산 목적에 적합한 근사치입니다.
등엔트로픽 흐름
유체역학에서 등엔트로픽 흐름은 단열적이고 가역적인 유체 흐름입니다.즉, 흐름에는 열이 추가되지 않으며 마찰 또는 산란 효과로 인한 에너지 변환이 발생하지 않습니다.완벽한 기체의 등방성 흐름의 경우, 유선을 따라 압력, 밀도 및 온도를 정의하기 위해 몇 가지 관계를 도출할 수 있습니다.
열교환이 발생하지 않는 한 에너지는 등엔트로픽 변환에서 흐름과 교환될 수 있습니다.이러한 교환의 예로는 흐름에서 또는 흐름에 의해 수행되는 작업을 수반하는 등엔트로픽 확장 또는 압축이 있습니다.
등엔트로픽 흐름의 경우 엔트로피 밀도는 유선마다 다를 수 있습니다.엔트로피 밀도가 어디에서나 같다면 흐름은 균질하다고 할 수 있습니다.
등엔트로픽 관계 도출
폐쇄형 시스템의 경우 시스템의 총 에너지 변화는 수행된 작업과 가해진 열의 합계입니다.
볼륨을 변경하여 시스템에서 실행 가능한 작업은 다음과 같습니다.
서 pp는 이고 VV는 볼륨입니다.엔탈피 변화량( + V{은 다음과 같습니다.
다음으로 가역적이면서도 단열적인 프로세스(즉, 열전달이 발생하지 않음)의 경우, 0(\rev}}=이므로 d (\ =\ 모두 가역적입니다.이를 통해 두 가지 중요한 관측치가 도출됩니다.
다음으로 이상기체의 등엔트로픽 프로세스를 크게 계산할 수 있다.이상적인 기체의 변환에 대해, 항상 다음과 같은 것이 사실이다.
- U d (\ dU 및 d C
위의(\dU) dH(\dH에 대한 일반적인 결과를 사용하여
따라서 이상적인 가스의 경우 열용량비는 다음과 같이 나타낼 수 있습니다.
열량이 완벽한 기체의 경우(\는 일정합니다.따라서, 위의 방정식을 적분하면, 열량적으로 완벽한 기체를 가정할 때, 우리는
그것은,
이상 기체에 대한 상태 방정식을 하여 p T\ \ =
(증명: V 상수 P - R - { PV^ { \ } ={ \ PV , \ { \ - 1 } text { 、 rightarrow { right . 그러나 nR = 상수이므로 ) - 1(\ TV -1}=}})
상수 p v + {\}=몰당)의 경우,
- T V p {})
따라서 이상적인 기체를 가진 등엔트로피 과정의 경우,
- ( V) ( / ) { } = (T ()
이상 기체에 대한 등엔트로픽 관계 표
유래
여기서:
- {\ P = 압력,
- {\ V = 볼륨,
- \display = 비열비 = / v { C _ { } / _{ v} ,
- {\ T = 온도,
- {\ m = 질량,
- s{\s}} = 특정 가스= / {\ R
- {\ R = 범용 가스 상수,
- 특정 가스의 분자량
- \rho} = ,
- p \ = 일정한 압력에서의 비열,
- v \ = 일정한 볼륨에서의 비열.
「 」를 참조해 주세요.
메모들
- ^ 를 클릭합니다Partington, J. R. (1949), An Advanced Treatise on Physical Chemistry., vol. 1, Fundamental Principles. The Properties of Gases, London: Longmans, Green and Co., p. 122.
- ^ 케스틴, J. (1966)Waltham MA, Blaisdell Publishing Company, 열역학 코스, 페이지 196.
- ^ Munnster, A.(1970년)고전 열역학, E. S. Halberstadt, Wiley-Intercience, 런던, ISBN 0-471-62430-6, 13페이지.
- ^ 하세, R. (1971년)열역학 제1장, 제1권 1~97쪽 기본 법칙 조사.물리 화학의 W. Jost입니다. 고급 논문, 에디션.H. 아이링, D.헨더슨, W. Jost, 뉴욕, 학술 출판사, lcn 73–117081, 페이지 71
- ^ Borgnakke, C., Sonntag., R.E. (2009)열역학의 기초, Wiley, 7판, ISBN 978-0-470-04192-5, 310페이지.
- ^ Massey, B. S.(1970), Mechanics of Fluids, 섹션 12.2 (제2판) Van Nostrand Reinhold Company, 런던.의회 도서관 카탈로그 카드 번호: 67-25005, 19페이지
- ^ § 첸겔, Y. A., Boles, M. A. (2015년)열역학: An Engineering 어프로치, 제8판, 뉴욕 McGraw-Hill, ISBN 978-07-339817-4,
- ^ § 첸겔, Y. A., Boles, M. A. (2015년)열역학: 엔지니어링 접근법, 제8판, 뉴욕 McGraw-Hill, ISBN 978-0-07-339817-4, 페이지 340-341.
- ^ Mortimer, R. G. Physical Chemistry, 제3판, 120페이지, Academic Press, 2008.
- ^ 페르미, E열역학, 48페이지 각주, 도버 출판물, 1956년(아직도 인쇄 중).
- ^ 구겐하임, E. A.(1985년)열역학. 화학자와 물리학자를 위한 고급 처리, 7판, North Holland, Amsterdam, ISBN 0444869514, 페이지 12: "자연적 과정과 부자연스러운 과정 사이의 제한적인 경우로서, 우리는 일련의 평형 상태를 통과하는 어느 방향의 통과로 구성된 가역적 과정을 가지고 있습니다.되돌릴 수 있는 프로세스는 실제로 발생하지 않습니다.."
- ^ 케스틴, J. (1966)Blaisdell Publishing Company, Waltham MA, 페이지 127: "그러나 상상력을 발휘하여 원하는 대로 프로세스, 압축 또는 확장을 무한히 느리게[, 또는 준정적으로] 실행할 수 있다는 것이 인정되었습니다." P 130: "모든 프로세스는 자연적이고 돌이킬 수 없는 것입니다."알기 쉬운 프로세스는 편리한 이상화만을 구성합니다."
- ^ a b 센겔, 유누스 A., 마이클 A.열역학:엔지니어링 어프로치제7판 ed.뉴욕:Mcraw-Hill, 2012.인쇄.
레퍼런스
- 밴 와일런, G. J.와 손태그, R. E.(1965), 클래식 열역학 기초, 존 와일리 & 선스, 뉴욕.의회도서관 카탈로그 카드번호: 65-19470
















 가열에 의해 시스템이 얻는 에너지량,
가열에 의해 시스템이 얻는 에너지량, 
 엔트로피의 변화입니다.등호란
엔트로피의 변화입니다.등호란 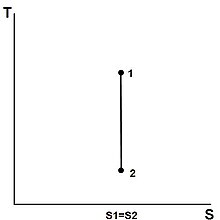
 압축기
압축기



 입구 상태의 특정
입구 상태의 특정  실제 프로세스의 출구 상태의 특정 엔탈피입니다.
실제 프로세스의 출구 상태의 특정 엔탈피입니다. 등엔트로픽 프로세스의 출구 상태의 특정 엔탈피입니다.
등엔트로픽 프로세스의 출구 상태의 특정 엔탈피입니다.





 d
d 








 일정합니다.따라서, 위의 방정식을 적분하면, 열량적으로 완벽한 기체를 가정할 때, 우리는
일정합니다.따라서, 위의 방정식을 적분하면, 열량적으로 완벽한 기체를 가정할 때, 우리는



 nR = 상수이므로
nR = 상수이므로 







































