전자기 입문

Introduction to electromagnetism
이 기사는 주제에 대한 개념적 이해에 관한 것이다.자세한 수학적 처리는 전자기장을 참조하십시오.

전자기기는 자연의 기본적인 힘 중 하나이다.초기에는 전기와 자성을 따로 연구하여 별개의 현상으로 간주하였다.Hans Christian örsted는 이 두 가지가 관련이 있다는 것을 발견했다. 즉 전류가 자성을 발생시킨다.마이클 패러데이는 자력이 전류를 유도할 수 있다는 사실을 발견했고 제임스 클럭 맥스웰은 모든 것을 전자기학의 통합 이론으로 정리했습니다.맥스웰의 방정식은 전자파가 존재한다는 것을 더 보여주었고, 하인리히 헤르츠의 실험으로 이를 확인함으로써 무선이 가능해졌다.맥스웰은 또한 빛이 전자파의 한 형태라고 정확하게 가정했고, 따라서 모든 광학을 전자기학의 한 분야로 만들었다.전파는 전자의 파장이 후자의 파장보다 훨씬 길다는 점에서 빛과 다르다.알버트 아인슈타인은 자기장이 전기장의 상대론적 운동을 통해 발생한다는 것을 보여주었고, 따라서 자기장은 전기의 부작용일 뿐이다.전자석의 현대 이론적인 처리는 양자 전기역학에서 양자장으로서의 것이다.

전기 공학에 관심이 있는 많은 상황에서는 올바른 결과를 얻기 위해 양자 이론을 적용할 필요가 없습니다.고전물리학은 거시적인 물체와 관련된 대부분의 상황에서 여전히 정확한 근사치이다.몇 가지 예외를 제외하고, 양자 이론은 원자 규모에서만 필요하며 더 간단한 고전적 처리가 적용될 수 있다.제한된 상황에서 치료를 더 단순화할 수 있습니다.정전기는 정지된 전하만을 다루므로 자기장이 발생하지 않으며 고려되지 않습니다.영구 자석은 전기나 전자기력을 고려하지 않고 설명할 수 있습니다.회로 이론은 전류가 흐르는 도체를 중심으로 필드가 제한되는 전기 네트워크를 다룹니다.이러한 회로에서는 Maxwell의 방정식조차 생략할 수 있고 간단한 공식을 사용할 수 있습니다.반면에, 전자기학의 양자 처리는 화학에서 중요하다.화학 반응과 화학 결합은 원자 주위의 전자의 양자 역학적 상호작용의 결과이다.터널 다이오드와 같은 많은 전자 장치의 동작을 설명하기 위해서는 양자 고려 사항도 필요합니다.

전하

쿨롱의 법칙은 비슷한 전하가 밀어내고 반대 전하가 끌어당긴다는 것을 말해준다.

전자기력은 중력, 강한 힘, 약한 힘과 함께 자연의 기본 힘 중 하나입니다.중력은 질량을 가진 모든 물체에 작용하는 반면, 전자기기는 전하를 가진 모든 물체에 작용한다.또한 질량을 생성하거나 파괴할 수 없는 질량의 보존이 존재하기 때문에 전하 보존도 존재하기 때문에 (전하가 나오거나 들어오지 않는) 닫힌 계통의 전하가 [1]일정하게 유지되어야 한다.고전 물리학에서 거대한 물체에 작용하는 중력을 설명하는 기본 법칙은 뉴턴의 중력의 법칙이다.이와 유사하게 쿨롱의 법칙은 대전된 물체가 서로에게 가하는 힘을 설명하는 기본 법칙입니다.그것은 식에 의해 주어진다.

여기서 F는 힘, k는e 쿨롱 상수1, q와2 q는 두 전하의 크기, r은2 둘 사이의 거리의 제곱입니다.같은 전하가 서로 밀어내는 반면 반대 전하가 서로 끌어당겨 입자의 전하가 강할수록 서로에게 가해지는 힘이 강해진다는 사실을 기술한 것이다.이 법칙은 또한 두 입자 사이의 거리가 두 배로 늘어나면 두 입자에 가해지는 힘이 [2]4배 감소한다는 것을 의미하는 역제곱 법칙이다.

전기장과 자기장

전계선은 양전하부터 음전하까지를 가리킵니다.
전기장(왼쪽)과 자기장(오른쪽)이 양전하에 가해지는 힘을 합쳐 로렌츠 힘을 얻는다.

물리학에서 장은 물질과 상호작용하는 실체이며 공간과 시간의 각 점에 값을 할당하여 수학적으로 설명할 수 있습니다.벡터 필드는 공간과 시간의 각 지점에서 수치와 방향을 모두 할당하는 필드입니다.전하가 전기장이라고 불리는 벡터장을 생성한다.전계 강도라고도 불리는 전계의 수치는 장에서 하전 입자가 느낄 전기의 강도를 결정하고 장 방향은 힘이 어느 방향으로 갈지를 결정합니다.관례상 전계의 방향은 정전하에서의 힘의 방향과 동일하고, [3][4]부전하에서의 힘의 방향과는 반대이다.양전하가 다른 양전하에 의해 격퇴되고 음전하에 끌리기 때문에 이는 전기장이 양전하로부터 멀어져 음전하를 가리킨다는 것을 의미합니다.전기장의 이러한 특성은 전기장의 관점에서 쓰여진 전하 위의 전기력에 대한 방정식에 요약되어 있습니다.

여기서 F는 전계 [4][5]E의 전하 q에 대한 힘이다.

전하 입자는 전계를 생성하는 것뿐만 아니라, 운동 중인 다른 전하(영구 [6]자석도 포함)에서 느낄 수 있는 운동 상태에 있을 때 자기장을 생성합니다.자기장으로부터의 전하 이동에 대한 힘의 방향은 운동 방향과 자기장 라인의 방향 모두에 수직이며 오른쪽 규칙을 사용하여 구할 수 있습니다.힘의 세기는 다음 식에 의해 주어진다.

여기서 F는 [7]전하 이동 방향에서 각도 θ 방향을 가리키는 자기장 B에서 속도 v를 갖는 전하 q에 대한 힘이다.

닫힌 표면으로 둘러싸인 전하가 없는 경우, 그 표면으로 유입되는 전계의 양은 닫힌 표면에서 흘러나오는 전계와 함께 정확히 상쇄되어야 합니다.
닫힌 표면에서 나오는 자기장의 흐름은 그 흐름과 함께 취소되어야 하기 때문에 자석은 단극으로 분리될 수 없는 북극과 남극을 모두 가져야 한다.

하전 입자에 가해지는 전기력과 자기력의 조합을 로렌츠력이라고 합니다.[7][8]고전 전자기학은 맥스웰 방정식이라고 불리는 일련의 방정식과 함께 로렌츠 힘에 의해 완전히 묘사된다.이 방정식들 중 첫 번째는 가우스의 법칙으로 알려져 있다.하전 입자와 전하 분포에 의해 생성되는 전계를 설명합니다.가우스의 법칙에 따르면 닫힌 표면을 통과하는 전계의 플럭스(또는 흐름)는 해당 [9][10]표면에 둘러싸인 전하량에 비례합니다.즉, 전하가 클수록 생성되는 전장이 커집니다.그것은 또한 다른 중요한 의미를 가지고 있다.예를 들어, 이 법칙은 표면에 의해 둘러싸인 전하가 전혀 없는 경우, 전계가 전혀 없는 경우, 또는 닫힌 표면과 가깝고 바깥쪽에 전하가 있는 경우 표면으로의 전계의 흐름이 [11]표면으로부터의 흐름과 정확히 상쇄되어야 한다는 것을 의미합니다.맥스웰 방정식의 두 번째 공식은 자력에 대한 가우스의 법칙으로 알려져 있고, 첫 번째 가우스의 법칙과 유사하게, 플럭스를 설명하지만, 전기 플럭스 대신 자속을 설명합니다.가우스의 자기 법칙에 따르면 닫힌 표면을 통과하는 자기장의 흐름은 항상 0입니다.즉, 자기장이 존재할 경우 닫힌 표면으로의 흐름은 닫힌 표면으로부터의 흐름과 함께 항상 상쇄됩니다.이 법칙은 닫힌 표면에서 흘러나오는 자속은 반드시 그 안으로 역류해야 한다는 것을 의미하기 때문에 "자기 단극이 아니다"라고 불리기도 합니다. 즉, 양극과 음극은 자기 단극으로 [12]합쳐져야 하며 절대 분리될 수 없습니다.이는 별도의 양전하와 음전하로 존재할 수 있는 전하와는 대조적입니다.

직선 와이어(왼쪽) 및 코일 와이어(오른쪽)의 오른쪽 그립 규칙입니다.철심 주위에 감긴 와이어를 통과하는 전류는 전자석을 생성할 수 있습니다.

맥스웰의 세 번째 방정식은 암페어-맥스웰 법칙이라고 불립니다.전류에 [13]의해 자기장이 발생할 수 있다고 명시되어 있습니다.자기장의 방향은 Ampér의 오른손 그립 규칙에 의해 지정됩니다.와이어가 직선일 경우 자기장은 오른손 법칙에서 쥐어진 손가락처럼 와이어 주위를 휘감습니다.와이어를 코일로 감으면 코일 내부의 자기장이 오른손 그립 [14]규칙에서 엄지손가락을 펴듯이 직선을 가리킵니다.이런 방식으로 자석을 생산하기 위해 전류가 사용될 때, 그것은 전자석이라고 불린다.전자석은 종종 철심 주위에 솔레노이드를 감아 올린 와이어를 사용합니다. 이 와이어는 철심이 [15][16]자화되기 때문에 발생하는 자기장을 강화합니다.맥스웰의 법칙에 대한 확장은 시변하는 전기장도 자기장을 [12]발생시킬 수 있다는 것이다.비슷하게, 패러데이의 유도 법칙은 자기장이 전류를 발생시킬 수 있다고 말한다.예를 들어 와이어 코일에 압출된 자석은 코일에 자석의 강도, 코일 수 및 코일에 자석이 삽입 및 추출되는 속도에 비례하는 전류를 발생시킬 수 있다.이 원리는 전류를 고전압에서 저전압으로 변환하는 데 사용되는 변압기에 필수적입니다.고전압 주전원을 가정에서 안전하게 사용할 수 있는 저전압 전기로 변환하는 데 필요합니다.맥스웰의 법칙 공식은 맥스웰-패러데이 방정식의 네 번째이자 마지막인 맥스웰-패러데이 방정식에 제시되어 있는데, 이 방정식은 시변하는 자기장이 전기장을 생성한다는 것을 나타냅니다.

전자기 스펙트럼

함께, 맥스웰 방정식은 전기장과 자기장의 단일 균일한 이론을 제공하며, 이 이론을 만든 맥스웰의 연구는 뉴턴의 [17]만유인력의 법칙의 첫 번째 대통합에 이어 "물리학의 두 번째 대통합"으로 불렸습니다.자유 공간(전하 또는 전류가 없는 곳)에서 맥스웰 방정식의 해는 [18]빛의 속도로 이동하는 전자파(전기 및 자기 성분 모두 포함)에 해당하는 파동 방정식을 생성합니다.이러한 파동 용액이 빛의 속도와 정확히 동일한 파속을 가지고 있다는 관찰은 맥스웰이 빛이 전자기 복사의 한 형태라는 가설을 세우고 다른 전자기 복사가 다른 [19]파장을 가지고 존재할 수 있다는 것을 단언하도록 이끌었습니다.전자기 복사의 존재는 1886년부터 1889년까지의 일련의 실험에서 하인리히 헤르츠에 의해 증명되었고, 그 실험에서 그는 전파의 존재를 발견했다.전체 전자기 스펙트럼(주파수 증가 순서대로)은 전파, 마이크로파, 적외선, 가시광선,[20] 자외선, X선 및 감마선으로 구성된다.

연구실 프레임
전자의 정지 프레임

전자기학의 추가적인 통합은 아인슈타인의 특수 상대성 이론과 함께 이루어졌다.특수상대성이론에 따르면, 서로 다른 속도로 움직이는 관측자는 서로 다른 관측 기준 프레임을 차지한다.만약 한 관찰자가 다른 관찰자에 대해 상대적으로 움직이고 있다면, 그들은 움직이지 않는 물체가 정지해 있는 관찰자보다 움직이는 관찰자에게 더 가까이 나타나는 길이 수축을 경험하게 됩니다.따라서 전자가 중성선에서 전류와 같은 속도로 움직이면 전선에서 흐르는 전자가 그에 대해 정지해 있고 양전하가 함께 수축되어 있는 것을 경험할 수 있습니다.실험실 프레임에서는 전자가 움직이고 있기 때문에 와이어의 전류에서 자력을 느끼지만 와이어가 중립이기 때문에 전기력이 느껴지지 않습니다.하지만 전자의 정지 프레임에서는 흐르는 전자에 비해 양전하가 서로 더 가까워 보이고 그래서 전선은 양전하를 띠는 것처럼 보입니다.따라서 전자의 정지 프레임에서는 자력이 느껴지지 않지만(자기 프레임 내에서 움직이지 않기 때문에), 양전하 와이어로 인해 전기적인 힘이 느껴집니다.이 상대성 이론의 결과는 자기장이 다른 기준 프레임의 전기장일 뿐이며, 따라서 이 둘은 동일한 기본 전자기장의 [21][22][23]다른 표현이라는 것을 증명합니다.

도체, 절연체 및 회로

컨덕터

완벽한 도체의 전하가 재배치되어 내부의 전계가 항상 0이 됩니다.

도체는 전자를 쉽게 흐르게 하는 물질이다.가장 효과적인 도체는 보통 금속인데, 그 이유는 전자가 원자핵에서 탈국소화되어 양이온이 자유 [24]전자 구름에 둘러싸인 자유 전자 모델에 의해 꽤 정확하게 설명될 수 있기 때문입니다.양호한 도체의 예로는 구리, 알루미늄 및 은이 있습니다.전자제품의 전선은 종종 [25]구리로 만들어진다.

도체의 주요 속성:[26] 있다.

  1. 전기 필드가 완전 도체 안에 0이다.왜냐하면은 전도체에서 자유롭게 움직이고 있을 때 외부 전계에 시달리고 있습니다. 그들은 자신이 그들의 배치가 생산해 내는 분야 정확하게 지휘자 안에 외부 전기장 가서 취소해 재정리하다.
  2. 그 전위는 어디나 지휘자가 안으로 들어가서는 도체의 표면을 가로질러 끊임 없는 것 같다.때문에 경기장은 zero는 모든 곳에 지휘자 안에 있었고, 따라서 잠재력이 지휘자 안에 너무 일정하다 이것은 처음 진술의 의미를 따른다.
  3. 전기 필드가 도체의 표면에 수직이다.만약에 그것이 아닌 경우, 필드가 지휘자의 혐의는 분야의 해당 구성 요소가 0까지 이사에 가져오실 그 지휘자의 표면에 조금이라도 구성 요소를 가지고 있을 것이다.
  4. 표면을 통해 최종 전기력 선속 배터리가 표면에 의해 둘려 싸여에 비례한다.가우스의 법칙. 이것은 다시 쓴 것일 뿐이다.

몇몇 물질들에서, 전자들은 원자 핵에 돌아다니는 것이 자유롭지 않지만 에너지 그들을 자유롭게 낮다 설정해야 하고 있었다.이러한 자료들에서 그 전도성을 저온에서 하지만 온도는 전자 더 열 에너지와 그 전도성 증가하며 얻는 증가한다 낮다 반도체라고 불렀다.[27]는 더 그들은 광자로부터 태양에서 얻은 더 많은 에너지 도전이 된 태양 전지판을 만드는 데 사용될 수 있는 반도체 실리콘은 한 예이다.[28]

전자의 흐름 때 특정의 임계 온도 이하로 냉각에 대한 면역력이 없 없는 것을 나타내Superconductors 있는 물질들.초전도 기술은 없다는 fermions(페르미온의 전자는 형식)정확히 같은 양자 상태를 차지할 수 있다고 언급하는 양자 기계적인 파울리의 배타 원리에 의해 설명될 수 있다.초전도체에서는 특정 온도 이하로, 전자 형태고 이 모든 전자는 같은 에너지 준위에 함께 한결같이 현재 이사 빠질 수 있다는 것 원칙을 따르지 않는 보손 범위 쌍입니다.[29]

절연체

유전체 재료에서 전계는 재료를 편광시킬 수 있다.

절연체는 전자의 흐름에 매우 저항성이 높은 물질이기 때문에 안전을 위해 전도선을 덮는 데 자주 사용됩니다.절연체에서는 전자가 원자핵에 단단히 결합되어 있고, 전자를 자유롭게 하기 위한 에너지가 매우 높아 이동이 자유롭지 않고 외부 [30]전계에 의해 유도되는 움직임에 저항한다.그러나 유전체라고 불리는 일부 절연체는 외부 전기장의 영향으로 분극될 수 있으므로 전하가 극소량 변위되어 양극과 음극이 [31]형성됩니다.유전체는 캐패시터 플레이트 사이의 전기장에 [32]더 많은 전위 에너지를 저장할 수 있도록 캐패시터에 사용됩니다.

콘덴서

평행판 콘덴서

콘덴서는 두 개의 반대 방향으로 대전된 전도판 사이의 전기장에 전위 에너지를 저장하는 전자 부품입니다.한쪽의 도체판이 +Q/A의 전하밀도를 가지며 다른 한쪽이 -Q/A의 전하를 가지면 A는 판의 면적이며, 그 사이에 전계가 생긴다.두 평행판 V 사이의 전위차는 수학적으로 다음과[33] 같이 도출될 수 있다.

여기서 d는 플레이트의 분리이고 00})은 여유 공간의 유전율입니다.캐패시터의 전기적 위치 에너지 저장 능력은 C / C로 정의된 캐패시턴스로 측정되며, 병렬 플레이트 캐패시터의 경우 다음과[33] 같습니다.

플레이트 사이에 유전체를 배치하면 자유 공간의 유전율에 유전체의 상대 유전율을 곱하여 정전용량을 [32]증가시킨다.콘덴서가[33] 저장할 수 있는 최대 에너지는 플레이트 간 전위차의 제곱과 정전 용량에 비례합니다.

인덕터

인덕터는 와이어 코일 내부의 자기장에 에너지를 저장하는 전자 부품입니다.전류 전달 코일은 Ampér의 회로 법칙에 따라 자기장을 유도합니다.전류 I가 클수록 자기장에 저장된 에너지가 커지고 인덕턴스가 낮아집니다. 인덕턴스는 I{ L=\ _ 여기서 { _는 와이어 코일에 의해 생성되는 자속입니다.인덕턴스는 전류 변화에 대한 회로 저항의 측정값이므로 인덕턴스가 높은 인덕터를 사용하여 [34]교류에 대항할 수도 있습니다.

기타 회로 구성 요소

요소 주요 기능 개략도 기호
저항기 전류 흐름을 방해합니다.
Resistor symbol America.svg
배터리 전원으로서 기능하다
Battery symbol.svg
직류 전압원 한 방향을 가리키는 정전류인 직류(DC)의 소스 역할을 합니다.
Voltage Source.svg
교류 전압원 주기적으로 방향을 반전시키는 가변 전류인 교류(AC)의 소스 역할을 합니다.
Alternative Current Symbol.png
다이오드 전류가 한 방향으로 쉽게 흐를 수 있지만 다른 방향으로 흐를 수 없습니다.
Diode symbol.svg
콘덴서 전기장에 에너지 저장, 전하 저장, 저주파 교류 전달
Capacitor symbol.svg
인덕터 자기장에 에너지를 저장하고 전류 변화에 저항합니다.
Inductor symbol.svg

회로 법칙

키르초프의 결합 규칙(위):

I1 + I2 + I3 = I4 + I5

Kirchoff의 루프 규칙(아래):

V1 + V2 + V3 + V4 = 0

회로 이론은 전류가 흐르는 도체를 중심으로 필드가 제한되는 전기 네트워크를 다룹니다.이러한 회로에서는 회로의 모든 동작을 전자기 법칙에서 직접 유도하는 대신 간단한 회로 법칙을 사용할 수 있습니다.옴의 법칙은 저항[35] R로 알려진 양을 도입하여 회로의 전류 I와 전압 V 사이의 관계를 나타냅니다.

옴의 법칙:

전력은 P P=)로 정의됩니다.옴의 법칙을 사용하여 회로의 힘을 다른 양으로[36] 나타낼 수 있습니다.

Kirchhoff의 결합규칙은 결합(또는 노드)에 들어가는 전류가 노드를 나가는 전류와 같아야 함을 나타냅니다.이는 전류가 시간에 따른 전하 흐름으로 정의되므로 전하 보존에서 비롯됩니다.전류가 접점을 빠져나갈 때 분할되면 결과적으로 분할된 전류의 합계는 유입 [37]회로와 동일합니다.

Kirchhoff의 루프 규칙은 회로 주위의 폐쇄 루프 전압의 합계가 0임을 나타냅니다.이는 전기장이 보수적이라는 사실에서 비롯됩니다. 즉, 어떤 경로를 택하든 간에 [37]한 지점에 다시 도달해도 전위는 변하지 않습니다.

규칙을 통해 [37]직렬 및 병렬 회로의 전류 및 전압과 같은 양을 합산하는 방법도 알 수 있습니다.

직렬 회로의 경우 각 구성 요소에 대해 전류가 동일하게 유지되고 전압과 저항이 합산됩니다.

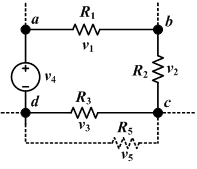
병렬 회로의 경우 전압은 각 구성 요소에 대해 동일하게 유지되며 전류 및 저항은 그림과 같이 관련됩니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ Purcell, Edward M. (21 January 2013). Electricity and magnetism (Third ed.). Cambridge. pp. 3–4. ISBN 978-1-107-01402-2. OCLC 805015622.
  2. ^ Walker, Jearl, 1945- (2011). Fundamentals of physics. Halliday, David, 1916-2010., Resnick, Robert, 1923-2014. (9th ed.). Hoboken, NJ: Wiley. p. 578. ISBN 978-0-470-46911-8. OCLC 435710913.{{cite book}}: CS1 maint: 여러 이름: 작성자 목록(링크)
  3. ^ Pumplin, Jon (2000). "Electric field lines". Michigan State University Physics. Retrieved 18 October 2018.
  4. ^ a b Nave, R. "Electric Field". Georgia State University Hyperphysics. Retrieved 16 October 2018.
  5. ^ Purcell, Edward M. (21 January 2013). Electricity and magnetism (Third ed.). Cambridge. p. 7. ISBN 978-1-107-01402-2. OCLC 805015622.
  6. ^ "The Feynman Lectures on Physics Vol. II Ch. 1: Electromagnetism". feynmanlectures.caltech.edu. Retrieved 2018-10-30.
  7. ^ a b "Magnetic forces". hyperphysics.phy-astr.gsu.edu. Retrieved 2020-11-26.
  8. ^ Purcell, Edward M. (21 January 2013). Electricity and magnetism (Third ed.). Cambridge. p. 277. ISBN 978-1-107-01402-2. OCLC 805015622.
  9. ^ Grant, I. S. (Ian S.) (1990). Electromagnetism. The Manchester Physics Series. Phillips, W. R. (William Robert) (2nd ed.). Chichester [England]: Wiley. pp. 17–22. ISBN 0-471-92711-2. OCLC 21447877.
  10. ^ "Gauss's Law". hyperphysics.phy-astr.gsu.edu. Retrieved 2018-10-30.
  11. ^ "The Feynman Lectures on Physics Vol. II Ch. 4: Electrostatics, S5: The flux of E". feynmanlectures.caltech.edu. Retrieved 2020-11-27.
  12. ^ a b Purcell, Edward M. (21 January 2013). Electricity and magnetism (Third ed.). Cambridge. p. 322. ISBN 978-1-107-01402-2. OCLC 805015622.
  13. ^ "Ampere's Law". hyperphysics.phy-astr.gsu.edu. Retrieved 2020-11-27.
  14. ^ Grant, I. S. (Ian S.) (1990). Electromagnetism. The Manchester Physics Series. Phillips, W. R. (William Robert) (2nd ed.). Chichester [England]: Wiley. p. 125. ISBN 0-471-92711-2. OCLC 21447877.
  15. ^ "Magnets and Electromagnets". hyperphysics.phy-astr.gsu.edu. Retrieved 2020-11-27.
  16. ^ "Ferromagnetism". hyperphysics.phy-astr.gsu.edu. Retrieved 2020-11-27.
  17. ^ Editors, AccessScience (2014). "Unification theories and a theory of everything". Access Science. doi:10.1036/1097-8542.BR0814141. {{cite journal}}: last=범용명(도움말)이 있습니다.
  18. ^ Grant, I. S. (Ian S.) (1990). Electromagnetism. The Manchester Physics Series. Phillips, W. R. (William Robert) (2nd ed.). Chichester [England]: Wiley. p. 365. ISBN 0-471-92711-2. OCLC 21447877.
  19. ^ Maxwell, James Clerk (1865). "A dynamical theory of the electromagnetic field" (PDF). Philosophical Transactions of the Royal Society of London. 155: 459–512. Bibcode:1865RSPT..155..459C. doi:10.1098/rstl.1865.0008. S2CID 186207827. Archived (PDF) from the original on 28 July 2011. Light and magnetism are affections of the same substance (p.499)
  20. ^ "Introduction to the Electromagnetic Spectrum and Spectroscopy Analytical Chemistry PharmaXChange.info". pharmaxchange.info. 2011-08-25. Retrieved 2020-11-26.
  21. ^ Purcell, Edward M. (2013). Electricity and magnetism (Third ed.). Cambridge. pp. 235–68. ISBN 978-1107014022. OCLC 805015622.
  22. ^ "The Feynman Lectures on Physics Vol. II Ch. 13: Magnetostatics". feynmanlectures.caltech.edu. Retrieved 2018-10-30.
  23. ^ A. 프랑스어(1968) 특수상대성이론, 8장 – 상대성과 전기, 페이지 229-65, W.W. 노튼.
  24. ^ Hook, J. R., Hall, H. E. (2010). Solid State Physics (2nd ed.). Chichester, West Sussex, U.K.: John Wiley & Sons. pp. 76–77. ISBN 978-1-118-72347-0. OCLC 868939953.{{cite book}}: CS1 maint: 여러 이름: 작성자 목록(링크)
  25. ^ "What Metals Make Good Conductors of Electricity?". Sciencing. Retrieved 2020-11-27.
  26. ^ Purcell, Edward M. (2013). Electricity and magnetism (Third ed.). Cambridge. p. 129. ISBN 978-1107014022. OCLC 805015622.
  27. ^ "The Feynman Lectures on Physics Vol. III Ch. 14: Semiconductors". feynmanlectures.caltech.edu. Retrieved 2020-11-26.
  28. ^ "How a Solar Cell Works". American Chemical Society. Retrieved 2020-11-26.
  29. ^ "The Feynman Lectures on Physics Vol. III Ch. 21: The Schrödinger Equation in a Classical Context: A Seminar on Superconductivity". feynmanlectures.caltech.edu. Retrieved 2020-11-26.
  30. ^ "Conductors and Insulators". hyperphysics.phy-astr.gsu.edu. Retrieved 2020-11-27.
  31. ^ "Dielectric physics". Encyclopedia Britannica. Retrieved 2020-11-27.
  32. ^ a b "Dielectrics". hyperphysics.phy-astr.gsu.edu. Retrieved 2020-11-27.
  33. ^ a b c Grant, I. S. (Ian S.) (1990). Electromagnetism. The Manchester Physics Series. Phillips, W. R. (William Robert) (2nd ed.). Chichester [England]: Wiley. pp. 41–42. ISBN 0-471-92711-2. OCLC 21447877.
  34. ^ Purcell, Edward M. (21 January 2013). Electricity and magnetism (Third ed.). Cambridge. p. 374. ISBN 978-1-107-01402-2. OCLC 805015622.
  35. ^ "Ohm's Law". hyperphysics.phy-astr.gsu.edu. Retrieved 2020-11-27.
  36. ^ "Electric Power". hyperphysics.phy-astr.gsu.edu. Retrieved 2020-11-27.
  37. ^ a b c Young, H. D., Freedman, R. A. (2016). Sears and Zemansky's University Physics with Modern Physics (14th ed.). Boston: Pearson. pp. 872–878. ISBN 978-0-321-97361-0. OCLC 897436903.{{cite book}}: CS1 maint: 여러 이름: 작성자 목록(링크)