지구 반지름

지구 반지름
지구 반지름
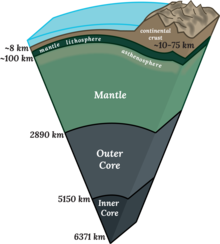	지구 내부의 단면
일반 정보
단위계	천문학, 지구물리학
단위	거리
기호.	E({ ({
변환
1🜨 R in...	...와 같다
SI 베이스 유닛	6.3781×106 m
미터법	6,357 ~ 6,378 km
영어 단위	3,963 mi (3,963 mi)

접지 반지름(R $R_{E}$ $R_{E}$ E $(\$ 로_🜨 표시됨)은 지구 중심에서 지표면 또는 지표면 근처 지점까지의 거리입니다.지구 구형에 의한 지구 수치와 근사한 반지름은 최대 6,378km(3,963mi)에서 최소 6,357km(3,950mi)(극성 반지름, b 표시)까지 다양하다.

천문학과 지구물리학에서는 공칭 지구반경을 측정 단위로 ^[1]사용하기도 하는데, 국제천문연맹은 이를 적도값은 국제천문연맹에서 권장하고 있다.

전지구 평균값은 보통 6,371km(3,959mi)로 간주되며, 다음과 같은 이유로 0.3%의 변동(±10km)을 보인다.국제 측 지학 지구 물리학(IUGG)의:3radii의 평균 반지름(기준선 R1)두 적도점과 남극에서 측정한;이와 같은 표면적(R2)과 구체의 반지름은 구체의 반지름은authalic 반경;그리고 체적 반경, ellips과 같은 볼륨을 3참조 값을 제공한다.oid(R₃).^[2] 3개의 값은 모두 약 6,371km(3,959mi)입니다.

지구의 반지름을 정의하고 측정하는 다른 방법으로는 곡률 반경이 있습니다.일부 정의는 국지적 또는 지리학적 지형을 포함하거나 추상적 기하학적 고려사항에 의존하기 때문에 극 반지름과 적도 반지름 사이의 범위를 벗어난 값을 산출한다.

서론

2003년 IERS 기준 타원체의 편평도(맨 위는 북쪽).하늘색 영역은 원입니다.진한 파란색 선의 바깥쪽 가장자리는 원과 단축이 같고 지구와 이심률이 같은 타원형이다.빨간색 선은 해발 100km(62mi)의 카르만 선을 나타내며, 노란색 영역은 낮은 지구 궤도에서 ISS의 고도 범위를 나타냅니다.

지구의 자전, 내부 밀도 변화, 외부 조력 등은 지구의 모양이 완벽한 ^[a]구체에서 체계적으로 벗어나게 합니다.국지적 지형은 편차를 증가시키고, 그 결과 표면은 매우 복잡해진다.지구 표면에 대한 우리의 설명은 다루기 쉽도록 실제보다 간단해야 한다.따라서 우리는 일반적으로 필요에 맞는 가장 단순한 모델에 의존하여 지구 표면의 특성을 대략적으로 추정하는 모델을 만듭니다.

일반적으로 사용되는 각 모델은 기하학적 반지름의 개념을 포함합니다.엄밀히 말하면, 구는 반지름을 가진 유일한 고체이지만, 반지름이라는 용어는 지구의 모형을 다루는 것을 포함한 많은 분야에서 널리 사용된다.다음은 지구 표면의 일부 모델 목록으로, 정확한 것부터 대략적인 것까지 순서대로 나열되어 있습니다.

지구의 실제 표면
실제 표면의 각 지점에서^[b] 평균 해수면으로 정의되는 지오이드는
회전 타원체라고도 불리는 구면체로 지구 전체를 모형화하거나^[c] 지역 작업을 위한 측지학
구

지오이드와 타원체의 경우 모델의 어느 지점에서 지정된 중심까지의 고정 거리를 "지구의 반지름" 또는 "지구의 반지름"^[d]이라고 합니다.또한 구면 모델의 평균 반지름을 "지구 반지름"이라고 부르는 것이 일반적입니다.반면, 지구의 실제 표면을 고려할 때, 일반적으로 실질적인 필요가 없기 때문에 "반경"을 언급하는 것은 드문 일이다.오히려 해수면 위나 아래 고도가 유용하다.

모델에 관계없이, 어떤 반지름도 극지방의 최소 약 6,357 km와 적도 최대 약 6,378 km (3,950에서 3,963 mi) 사이에 있다.따라서, 지구는 대부분의 맥락에서 구면 모델을 지지하고 "지구의 반지름"이라는 용어를 정당화하는 완벽한 구면으로부터 불과 3분의 1만 벗어납니다.구체적인 값은 다르지만, 이 기사의 개념은 모든 주요 행성에 대해 일반화됩니다.

지구 변형의 물리학

행성의 회전은 적도에서 부풀어 오르고 북극과 남극에서 평평해지는 타원형 타원체/구체에 근접하게 하여 적도 $반지름$ a가 극 $반지름$ b보다 약 $aq$ 더 커지도록 합니다.편평도 $상수$ q는 다음과 같이 구한다.

{{displaystyle q} = flac {a^{3}\obega ^{2}} {GM}},},}

여기서 $θ$ 는 각진동수, $G$ 는 중력 $상수$ , ^[e]M은 행성의 질량이다.지구.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}..mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1/q ≈ 289명은 가깝게는 측정된 역에 1/f ≈ 298.257을 펑크 내다.또한, 적도의 팽대부는 느린 변화를 보여줍니다.팽창은 감소하고 있었지만, 1998년 이후 팽창이 증가했는데, 아마도 ^[4]해류를 통한 해양 질량의 재분배 때문일 것이다.

밀도와 지각 두께의 변화는 표면과 시간에 따라 중력을 변화시키므로 평균 해수면이 타원체와 다르다.이 차이는 지오이드 높이이며, 타원체 위 또는 바깥쪽에서 양의 값이고, 아래 또는 안쪽에서 음의 값입니다.지오이드 높이 변화는 지구에서 110m(360ft) 미만이다.지진(예: 수마트라-안다만 지진)이나 얼음 덩어리의 감소(^[5]예: 그린란드)로 인해 지오이드 높이가 갑자기 변할 수 있습니다.

모든 변형이 지구 내에서 발생하는 것은 아니다.달이나 태양으로부터의 중력은 주어진 지점의 지구 표면을 거의 12시간 동안 10분의 1미터씩 변화시킵니다(지구 조수 참조).

반지름 및 로컬 조건

지구 반지름 계산을 위한 Al-Biruni의 방법(973–1048)은 서로 떨어진 두 위치에서 측정하는 것과 비교하여 원둘레를 측정하는 것을 단순화했다.

표면 높이에 대한 국지적 및 일시적인 영향을 고려할 때, 아래에 정의된 값은 "일반 목적" 모델에 기초하며, 기준 타원체 높이로부터 5m(16ft) 이내 및 평균 해수면으로부터 100m(330ft) 이내(지질 높이 제외)로 가능한 한 정확하게 세분화된다.

또한 반지름은 한 지점에서 지구의 곡률로부터 추정할 수 있습니다.원환과 마찬가지로 한 지점에서 곡률은 한 방향(지구상에서 북쪽에서 남쪽)에서 가장 크고(가장 평평한) 수직(동쪽에서 서쪽)에서 가장 작습니다.해당 곡률 반경은 해당 지점에서 측정되는 위치와 방향에 따라 달라집니다.그 결과 적도에서 진정한 지평선까지의 거리가 동서 방향보다 남북 방향이 약간 더 짧습니다.

요약하자면, 지형의 국지적 변화로 인해 단일 "정확한" 반지름을 정의할 수 없습니다.이상적인 모델만 채택할 수 있다.Eratostenes의 견적 이후 많은 모델이 생성되었습니다.역사적으로 이러한 모델은 지역 지형을 기반으로 조사 대상 지역에 가장 적합한 기준 타원체를 제공한다.위성 원격 감지, 특히 위성 측위 시스템의 중요성이 높아짐에 따라, 지역 작업에는 정확하지 않지만 지구 전체에 가장 가까운 진정한 글로벌 모델이 개발되었습니다.

극지점: 적도 및 극지름

다음 반지름은 WGS-84(^[6]World Geodetic System 1984) 기준 타원체에서 도출되었다.이것은 이상적인 표면이며, 이를 계산하는 데 사용되는 지구 측정치는 적도 ^[7]및 극지원에서 ±2m의 불확실성을 가진다.특정 위치의 지형적 변화로 인해 추가적인 불일치가 발생할 수 있습니다.관측 가능한 위치의 위치를 식별할 때 WGS-84 반지름에 더 정확한 값을 사용해도 정확도가 ^{[clarification needed]}개선되지 않을 수 있다.

적도 반지름 값은 WGS-84에서 가장 가까운 0.1m로 정의되어 있습니다.이 섹션의 극 반지름 값은 대부분의 용도에 적합할 것으로 예상되는 가장 가까운 0.1m로 반올림되었다.극반경의 보다 정확한 값이 필요한 경우 WGS-84 타원체를 참조하십시오.

지구의 적도 $반지름$ a 또는 반장축은 중심에서 적도까지의 거리로 6,378.1370 km (3,963.1906 mi)^[8]와 같다.적도 반경은 종종 지구와 다른 행성들을 비교하는데 사용된다.

지구의 극 $반지름$ b 또는 반소형 축은 중심에서 북극과 남극까지의 거리로 6,356.7523 km(3,949.9028 mi)와 같다.

위치 의존 반지름

지구 위도의 함수로 세 개의 다른 반지름이 있습니다.

R

은 지심반경,

M

은 곡률반경,

N

은 곡률의 주요 수직반경입니다.

지심 반지름

지심 반지름은 지구 중심에서 지구 위도 $θ$ 에서 구상 표면의 지점까지의 거리이다.

R(\varphi)={frac {(a^{2}\cos \varphi)^{2}+(a\cos \varphi)^{2}+(b\sin \varphi)^{2}}}}}

$여기$ 서 $a$ 와 b는 각각 적도 반지름과 극 반지름이다.

타원체의 극지점 반지름은 적도 반지름과 극 반지름과 일치한다.이들은 타원의 꼭지점이며 곡률의 최소 및 최대 반지름과도 일치합니다.

곡률 반지름

곡률의 주반경

곡률에는 두 가지 주요 반경이 있습니다. 즉, 1년 단위 정규 섹션과 소수-수직 정규 섹션입니다.

자릿수

특히, 지구의 (북-남) 자오선 방향의 (북-남) 곡률 반지름은 $다음$ 과 같다.

{{displaystyle M(\varphi)}=bigfrac {(ab)^2}{\big (a\cos \varphi)^{2}+(b\sin \varphi)^2}{\big}}}{\frac {3}}=bigfrac {a(1-e^2}}{\b}{\b}{\big}}}{\bigfrac {\b}}}}{\frac {\b}}}{\frac {\frac {\b}}}}}}}}{\frac}

$여기$ 서 e $\displaystyle$ e는 $e$ 지구의 편심률입니다.이것은 에라토스테네스가 아크 측정에서 측정한 반지름입니다.

프라임 수직

prime vertical radius라고 불리는 PQ의 길이는

N(\phi )

(

N(\phi )

){

displaystyle

N ( \

phi

)

N(\phi )

。IQ 길이는 e

\,e^{2}N(\phi )

(

\,e^{2}N(\phi )

) {

displaystyle

,

e^{2}

N

\,e^{2}N(\phi )

( \

phi

)

\,e^{2}N(\phi )

} .

R=(X,\,Y,\,Z)

R=(X,\,Y,\,Z)

(

X

,

R=(X,\,Y,\,Z)

,

R=(X,\,Y,\,Z)

) {

displaystyle

R

=

( X , Y ,

Y

, Z

R=(X,\,Y,\,Z)

)

R=(X,\,Y,\,Z)

} 입니다.

한 점이 다른 점의 정확히 동쪽에 나타났다면, 한 점은 동쪽-서쪽 ^[f]방향으로 대략적인 곡률을 구한다.

지구의 곡률 횡단 반지름이라고도 불리는 이 지구의 원시-수직 곡률 반경은 측지 $위도$ $θ$ 에서 M에 수직(직교)으로 정의된다.^[g]

N(\varphi)=syn frac {a^{2}{\sin \varphi}{2}}=syn frac {a}{\sin rt {1-e^2}\sin ^2}\varphi}},

N은 타원체 표면에서 극축까지의 ^[9]법선 거리로 기하학적으로 해석될 수도 있습니다.위도 평행선의 반지름은 p $p=N\cos(\varphi )$ $p=N\cos(\varphi )$ cos $p=N\cos(\varphi )$ θ ( $p=N\cos(\varphi )$ ) { $displaystyle$ p $=N\cos(\varphi$ )} $p=N\cos(\varphi )$ ^[10]로 $p=N\cos(\varphi )$ 됩니다.

극지 및 적도 곡률 반지름

적도에서 지구의 곡률 반지름은 자오선의 반위도와 같습니다.

b 2 / a

= 6,335.439km

적도에서 지구의 주요-최소-최소 곡률 반경은 $적도$ $반지름$ N = a와 같다.

지구의 극곡률 반지름(수선 또는 소수-수직)은 다음과 같다.

a 2 / b

= 6,399.594km

파생

확장 콘텐츠

주요 곡선은 ^[11]다음에서 방정식(125)의 근이다.

\displaystyle (EG-F^{2}),\kappa ^{2}-(eG+gE-2F),\kappa +(e-f^{2})=0=\det(A-\kappa,B),

여기서 표면의 첫 번째 기본 형태(의 식(112):

\displaystyle ds^{2}=\sum _{ij}a_{i}dw^{j}=E,d\varphi^{2}+2F,d\varphi,d\varphi,d\bda +G,d\lambda ^{2}

E, F 및 G는 메트릭 텐서의 요소이다.

{\displaystyle A=a_{ij}=\sum _{\nu}{\frac {\frac r^{\frac w^{i}}{\frac {\frac w^{\nu}}}=\left[\begin{array}{l}E&F}{\f}\F&G\end{array}\right],

$r=[r^{1},r^{2},r^{3}]^{T}=[x,y,z]^{T}$ ${T}=[x,y,z]^$ ${T$ $w^{1}=\varphi$ 1 $w^{1}=\varphi$ ${\$ { $displaystyle$ w $^{1$ } = \ $varphi$ $w^{2}=\lambda ,$ $w^{2}=\lambda ,$ $w^{2}=\lambda ,$ 、 $w^{2}=\lambda ,$ 、 \ $displaystyle$ w $^{2$ } = \ $displayda$ , $w^{2}=\lambda ,$ }

표면의 두 번째 기본 형식(의 등식(123):

2D=\sum _{ij}b_{i}bc^{j}bc^{j}=e,d\varphi ^{2}+2f,d\varphi 、,d\varphi 、,d\g,d\varphi ^{2

e, f 및 g는 형상 텐서의 요소이다.

{\displaystyle B=b_{ij}=\sum _{\nu }n^{\nu}{\frac {\frac ^{i}\param w^{j}}=\left[{\f\f&g\endarray}}},

$n={\frac {N}{|N|}}$ $n={\frac {N}{|N|}}$ $displaystyle$ n = $flac {N$ } { N $}$ )은 $n={\frac {N}{|N|}}$ r $({displaystyle$ r $r$ 의 지표면 정규 단위입니다. ${\frac {\partial r}{\partial \varphi }}$ 는 ${\frac {\partial r}{\partial \varphi }}$ r $({displaystyle$ r} ${\$ displaystyle \ $frac$ ${\frac {\partial r}{\partial \lambda }}$ r} {\ $varphi$ }}}} ${\frac {\partial r}{\partial \lambda }}$ $({$ r $})$ 이)에서 tangda l(\ $da$ r)의 접선)은 ${\frac {\partial r}{\partial \lambda }}$ r)에서 표준 단위이기 때문입니다 $.$

N=brack\varphi}}\times {\frac\varphi}{\times {\frac r

r $\displaystyle$ 에서 지표면에 정상입니다.

타원형 $F=f=0$ 의 경우 $F=f=0$ f $F=f=0$ 0 {\displaystyle $F=f=0}$ 일 $F=f=0$ 때 곡선도는 다음과 같습니다.

\kappa _{1}={\frac {g}{G}}

1

\kappa _{1}={\frac {g}{G}}

=

\kappa _{1}={\frac {g}{G}}

\

displaystyle

\

kappa _

{ 1 } =

\kappa _{2}={\frac {e}{E}}\,,

frac

\kappa _{2}={\frac {e}{E}}\,,

{

g

} { G

\kappa _{1}={\frac {g}{G}}

} and 2 2 2

\kappa _{2}={\frac {e}{E}}\,,

\kappa _{2}={\frac {e}{E}}\,,

=

E , , {

2 displaystyle

\

kappa _

{

e

} , }

곡률의 주요 반지름은

R_{1}={\frac {1}{\kappa _{1}}}

1

R_{1}={\frac {1}{\kappa _{1}}}

R_{1}={\frac {1}{\kappa _{1}}}

R_{1}={\frac {1}{\kappa _{1}}}

1 {

display style

R_

{1} =

1

2

1 { \

kappa _

{

}

} 、

R_{2}={\frac {1}{\kappa _{2}}}.

2

R_{2}={\frac {1}{\kappa _{2}}}.

R_{2}={\frac {1}{\kappa _{2}}}.

R_{2}={\frac {1}{\kappa _{2}}}.

2

R_{2}={\frac {1}{\kappa _{2}}}.

. { \

displaystyle R_

{ }

=

1 2 2 . { \

kappa _

{

}

} 。

}

곡률의 첫 번째 반지름과 두 번째 반지름은 각각 지구의 곡률의 반지름과 소수-수직 반지름에 해당합니다.

기하학적으로 두 번째 기본 형태는 $r+dr$ r+ $r+dr$ $r+dr$ \ $displaystyle$ r + $dr$ \ displaystyle r \ dr \ $displaystyle$ r $r$ \ \ $dr$ \ at $r+dr$ at at at at at접면까지의 거리를 나타냅니다.

복합 곡률 반지름

방위각

지구의 방위 곡률 반경은 방위각(북쪽에서 시계 방향으로 측정) $α$ 와 위도 $θ$ 에서 지구 정규 구간을 따라 오일러의 곡률 공식에서 다음과 같이 ^[12]^{: 97}구한다.

R_{\mathrm {c} = flac {1} {\dfrac {cos ^{2}\alpha } {M}} + {\dfrac {sin ^{2}\alpha }}}},

비방향성

위의 곡률의 주반경을 무방향으로 조합할 수 있습니다.

위도 $θ$ 에서 지구의 가우스 곡률 반경은 다음과 같습니다.^[12]

R_{\mathrm {a} }(\varphi)=snapfrac {1} {2\pi}}=int _{0}^{2\pi }R_{\mathrm {c} }(\alpha), d\alpha =naphapa {Mnapa} ^2} {napa}

여기서 K는 가우스 곡률이며, $K=\kappa _{1}\,\kappa _{2}={\frac {\det \,B}{\det \,A}}$ $=$ $K=\kappa _{1}\,\kappa _{2}={\frac {\det \,B}{\det \,A}}$ $K=\kappa _{1}\,\kappa _{2}={\frac {\det \,B}{\det \,A}}$ = $K=\kappa _{1}\,\kappa _{2}={\frac {\det \,B}{\det \,A}}$ $=$ $K=\kappa _{1}\,\kappa _{2}={\frac {\det \,B}{\det \,A}}$ B $K=\kappa _{1}\,\kappa _{2}={\frac {\det \,B}{\det \,A}}$ A $K=\kappa _{1}\,\kappa _{2}={\frac {\det \,B}{\det \,A}}$ { $display style$ K=\ $kappa$ _ ${1},\kappa$ _ ${2$ }= $twfrac$ {\ $det$ \, $B}{\$ det \, $A$ 입니다.

위도 $θ$ 에서 지구의 평균 곡률 반지름은 다음과 같다.^[12]^{: 97}

R_{\mathrm {m}}=black {2}{\dfrac {1}{M}}+{\dfrac {1}{N}}}},\!

전역 반지름

지구는 여러 가지 방법으로 구체로 만들어질 수 있다.이 섹션에서는 일반적인 방법에 대해 설명합니다.여기서 도출된 다양한 반지름은 WGS-84 타원체에서 ^[6]도출된 지구 표기법과 치수를 사용한다.

적도 반지름:

a

= (6378.1370km)

극지름:

b

= (6356.7523 km)

구면 자체는 지오이드의 근사치이며, 이 구면에는 측지학에 적합한 밀리미터 분해능이 아닌 킬로미터 단위로 주어진다.

공칭 반지름

천문학에서 국제천문연맹(International Union)은 지구의 공칭 반지름을 ${\mathcal {R}}_{\mathrm {eE} }^{\mathrm {N} }$ $({style {mathcal {$ R $}_{\$ mathrm { $e$ 으로 나타내며, 이는 6,378.1 km(3,963.2 mi)^[1]^{: 3}로 정의된다.공칭 극지름의 정의는 R ${\mathcal {R}}_{\mathrm {pE} }^{\mathrm {N} }$ E ${\mathcal {R}}_{\mathrm {pE} }^{\mathrm {N} }$ {\ $displaystyle$ {\ $mathcal {R}}_{\mathrm {pE}}^{\mathrm {N}}$ = ${\mathcal {R}}_{\mathrm {pE} }^{\mathrm {N} }$ 6,356.8km(3,949.9mi)입니다.이 값들은 지구 0조 규칙에 해당합니다.일반적으로 극반경이 명시적으로 필요하지 않는 ^[1]^{: 4}한 적도반경은 공칭값으로 사용된다.공칭 반지름은 천문학의 길이 단위이다.(표기는 다른 행성에 대해 쉽게 일반화할 수 있도록 정의되어 있습니다. 예를 ${\mathcal {R}}_{\mathrm {pJ} }^{\mathrm {N} }$ , ${\mathcal {R}}_{\mathrm {pJ} }^{\mathrm {N} }$ ${\mathcal {R}}_{\mathrm {pJ} }^{\mathrm {N} }$ J ${\mathcal {R}}_{\mathrm {pJ} }^{\mathrm {N} }$ N (\ $displaystyle$ {\ $mathcal {R}_$ }})

산술 평균 반지름

1984년 세계지질계 개정판에 정의된 적도(a), 극지름(b) 및 산술 평균 지구 반지름(척도 없음)

지구물리학에서, 국제지질물리학연합(IUG)은 지구의 산술 평균 반지름( $R$ 로₁ 표시됨)을 다음과^[2] 같이 정의한다.

R_{1}=blac {2a+b}{3}}\,\!

2의 인수는 3축 타원체의 특성화인 지구 구상체의 2축 대칭을 설명한다.지구의 경우 산술 평균 반지름은 6,371.0088km(3,958.7613mi)^[13]입니다.

오토할라 반지름

지구의 자동 반지름 ("동일한 면적"을 의미)은 기준 타원체와 동일한 표면적을 가진 가상의 완벽한 구의 반지름이다.IUG는 자동 반경을 ^[2]R로 $나타냅니다 2$ .타원체에 ^[14]대해 폐쇄형 솔루션이 있습니다.

({displaystyle R_{2}=sqrt {frac {a^{2}+{\frac {b^{2}}{e}}\ln {leftfc\frac {1+e}{b/a}}\right)}}{2}}=sqrt {\frac {a^{2}}{\frac {b^{2}}{2}}}{\frac {\tanh ^{-1}e}{e}}}}=sqrt {4\pi }},},}

$여기$ 서² e $= a 2$ - b $/ a 2 2$ 및 $A$ 는 구상체의 표면적이다.

지구의 경우 자동 반경은 6,371.0072km(3,958.7603mi)^[13]입니다.

또한 $R_{2}$ ({ $style R_{$ 2})는 $R_{2}$ 타원체 표면에 걸친 가우스 곡률 K $({style$ K $K$ 의 평균을 구하여 얻은 (글로벌) 평균 곡률의 반지름에 해당합니다.가우스-보넷 정리를 사용하여, 이것은 다음과 같다.

디스플레이 스타일 {\frac\int K,dA\A}}=flac {4\pi}{A}}=flac {1}{R_{2}^{2}}}.}

체적 반지름

또 다른 구면 모델은 지구의 부피 반지름으로 정의되는데, 이것은 타원체와 같은 부피 구의 반지름이다.IUG는 체적 반경을 ^[2]R로 $나타냅니다 3$ .

({displaystyle R_{3}=sqrt[{3}]{a^{2}b}}),}

지구의 경우 부피 반지름은 6,371.0008km(3,958.7564mi)^[13]와 같습니다.

정류 반지름

또 다른 지구 반지름은 지구의 정류 반지름으로, 타원체의 극단면으로 묘사되는 타원의 둘레와 같은 구를 제공합니다.극성 및 적도 반지름을 고려할 때 이를 찾으려면 타원 적분이 필요합니다.

M_{\mathrm {r} = pi }} int _ {0}^{\frac {pi } {2} {\cos rt {a^{2}\varphi + {b^{2}}}\sin ^{2}\varphi }}},d\varphi,

정류 반경은 ^[14]M의 $평균값$ 으로 정의되는 1차 평균과 동일합니다.

M_{\mathrm {r} = flac {2}{\pi }}\int _{0}^{\frac {pi }{2}}\!M(\varphi), d\varphi,

통합 한계 [0, $θ$ /2]의 경우, 반지름과 평균 반지름을 정류하기 위한 적분은 동일한 결과로 평가되며, 지구의 경우 6,367.4491km(3,956.5494mi)에 달한다.

자오선 평균은 두 ^{[citation needed]}축의 반고정 평균에 의해 잘 근사됩니다.

{\displaystyle M_{\mathrm {r}\about \left({\frac {a^{\frac {3}{2}})+b^{\frac {2}{2}}{\right}^{\frac {2}{3}},})

이는 정확한 결과와 1μm(4×10인치⁻⁵) 미만으로 차이가 난다. 즉, 두 축의 평균은

M_{\mathrm {r}}\약 {frac {a+b}{2}},

약 6,367.445km(3,956.547mi)를 사용할 수도 있습니다.

지형 반지름

위의 수학식은 타원체 표면에 적용됩니다.아래 사례에서는 기준 타원체 위 또는 아래에 있는 지구의 지형을 고려합니다.따라서 위도에 따라 달라지는 지형적 지심 거리 R이다_t.

지형적 극한

최대_t R: 침보라조의 정상은 지구 중심에서 6,384.4km(3,967.1mi) 떨어져 있다.
최소_t R: 북극해 바닥은 지구 ^[15]중심에서 약 6,352.8km(3,947.4mi) 떨어져 있다.

지형적 전역 평균

지형 평균 지심 거리는 모든 곳의 평균 고도를 나타내며, 결과적으로 IUG 평균 반지름, 자동 반지름 또는 체적 반지름보다 230m 더 큰 값이 된다.이 지형 평균은 6,371.230km(3,958.899mi)이며, 불확실성은 10m(33ft)^[16]이다.

파생 수량: 지름, 원주, 호 길이, 면적, 부피

지구의 지름은 단순히 지구 반지름의 두 배입니다. 예를 들어, 적도 지름과 극지름입니다. 극지름 (2b)입니다.WGS84 타원체의 경우 각각 다음과 같습니다.

$2a$ = $12,756.2740km(7,926.3812mi),$
$2b$ = $12,713.5046km(7,899.8055mi).$

지구의 둘레는 둘레의 길이와 같다.적도 둘레는 단순히 원 둘레입니다.C_e=2µa, 적도 반지름의 경우 a.극 둘레는 C=4m로_p_p, 극 반지름 b가 편심 e=(1-b²/a²)^0.5를 통해 들어가는 자오선_p m=aE(e)의 4배입니다. 자세한 내용은 Ellipse#Circum을 참조하십시오.

자오선 호나 측지선과 같은 보다 일반적인 표면 곡선의 호 길이는 지구의 적도와 극 반지름에서 얻을 수 있습니다.

지도 투영 또는 측지 다각형에 기반한 지표면 면적도 마찬가지입니다.

지구의 부피 또는 기준 타원체의 부피는 V = 4/3µab이다².WGS84 회전 타원체의 매개변수를 사용하여 a = 6,378.137 km 및 b = 6356.7523142 km, V = 1.08321×10¹²³ km(2.5988¹¹×10 cu mi).^[17]

공개된 값

이 표는 지구 반지름에 대해 허용되는 값을 요약한 것입니다.

대리점	묘사	값(미터 단위)	참조
IAU	명목상의 '제로 밀물' 적도	6378100	^[1]
IAU	공칭 '제로 밀물' 극지방	6356800	^[1]
껴안다	적도 반지름	6378137	^[2]
껴안다	반소축(b)	6356752.3141	^[2]
껴안다	극곡률 반지름(c)	6399593.6259	^[2]
껴안다	평균 반지름(R₁)	6371008.7714	^[2]
껴안다	동일 표면의 구 반지름(R₂)	6371007.1810	^[2]
껴안다	같은 체적의 구 반지름(R₃)	6371000.7900	^[2]
IERS	WGS-84 타원체, 반장축(a)	6378137.0	^[6]
IERS	WGS-84 타원체, 반단축(b)	6356752.3142	^[6]
IERS	WGS-84 타원체, 극곡률반경(c)	6399593.6258	^[6]
IERS	WGS-84 타원체, 반축의 평균 반지름(R₁)	6371008.7714	^[6]
IERS	WGS-84 타원체, 등면적 구면 반지름(R₂)	6371007.2011	^[6]
IERS	WGS-84 타원체, 등체구 반지름(R₃)	6371000.7900	^[6]
	GRS 80 반장축(a)	6378137.0
	GRS 80 반단축(b)	© 6356752.314140
	구면 지구 반지름 약(R_E)	6366707.0195	^[18]
	적도의 곡률 반지름	6335439
	최대(침보라조 정상)	6384400	^[15]
	최소(북극해 바닥)	6352800	^[15]
	중심에서 지표면까지의 평균 거리	6371230±10	^[16]

역사

지구의 크기에 대한 첫 번째 출판된 언급은 기원전 350년경에 나타났는데, 그 때 아리스토텔레스는 그의 저서 "하늘에^[19] 대하여"에서 수학자들이 지구의 둘레를 40만 스타디아로 추정했다고 보고했다.학자들은 아리스토텔레스의 모습이 매우 정확한^[20] 것에서부터 거의 두 배의 ^[21]진가를 지닌 것으로 해석해 왔다.지구 둘레에 대한 최초의 과학적 측정과 계산은 기원전 240년 에라토스테네스에 의해 수행되었다.Eratostenes 측정 정확도 추정치는 0.5%에서 17%^[22] 사이입니다.아리스토텔레스와 에라토스테네스 모두에게, 그들의 추정의 정확성의 불확실성은 그들이 의미하는 스타디온 길이에 대한 현대의 불확실성 때문이다.

「」를 참조해 주세요.

메모들

^ 자세한 내용은 지구, 지오이드 및 지구 조수의 수치를 참조하십시오.
^ 지오이드에는 하나의 중심이 없으며 지역 측지 조건에 따라 달라집니다.
^ 지구중심 타원체에서, 타원체의 중심은 지구의 계산된 중심과 일치하며, 지구 전체를 가장 잘 모델링합니다.측지 타원체는 지질의 지역적 특성에 더 적합하다.타원체의 일부 표면이 영역에 적합하며, 이 경우 타원체의 중심과 방향이 일반적으로 지구의 질량 중심이나 회전 축과 일치하지 않습니다.
^ 반지름 값은 타원체 모델의 경우 위도에 따라 완전히 달라지며 지오이드에 따라 거의 달라집니다.
^ 이는 국제천문연맹의 정의 규칙(2)에 따른 것이다.행성은 중력과 원심력이 거의 ^[3]균형을 이루는 정수적 평형에 의해 형태를 띠게 된다.
^ 동서 방향은 오해의 소지가 있습니다.A에서 정동으로 나타나는 점 B는 A보다 적도에 더 가까울 것이다.따라서 이 방법으로 발견된 곡률은 적도를 제외하고 일정한 위도의 원의 곡률보다 작습니다.이 논의에서는 서쪽과 동쪽을 교환할 수 있다.
^ $N$ 은 특정 관심 지점의 타원체 표면과 자오선을 통과하는 평면에서의 곡률 반경으로 정의된다.

레퍼런스

^ ^a ^b ^c ^d ^e ^f Mamajek, E. E; Prsa, A; Torres, G; et al. (2015). "IAU 2015 Resolution B3 on Recommended Nominal Conversion Constants for Selected Solar and Planetary Properties". arXiv:1510.07674 [astro-ph.SR].
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j 모리츠, H. (1980년)1980년 캔버라에서 열린 IUG의 17I 총회 결의에 의한 측지 참조 시스템.
^ IAU 2006 총회: IAU 결의안 투표 결과 2006-11-07년 웨이백 머신에 보관
^ 2002년 8월 1일, 고다드 우주 비행 센터에서 인공위성이 지구 중력장의 큰 변화의 신비를 밝히고 있다.
^ 2005년 12월 20일, 고다드 우주 비행 센터, 그린랜드가 더 빨리 녹는 것을 발견한 NASA의 그레이스.
^ ^a ^b ^c ^d ^e ^f ^g ^h "WGS84RPT.tif:Corel PHOTO-PAINT" (PDF). Retrieved 2018-10-17.
^ "Info" (PDF). earth-info.nga.mil. Archived from the original (PDF) on 2020-08-04. Retrieved 2008-12-31.
^ "Equatorial Radius of the Earth". Numerical Standards for Fundamental Astronomy: Astronomical Constants : Current Best Estimates (CBEs). IAU Division I Working Group. 2012. Archived from the original on 2016-08-26. Retrieved 2016-08-10.
^ Bowring, B. R. (October 1987). "Notes on the curvature in the prime vertical section". Survey Review. 29 (226): 195–196. doi:10.1179/sre.1987.29.226.195.
^ Bomford, G. (1952). Geodesy. OCLC 489193198.
^ ^a ^b ^c Lass, Harry (1950). Vector and Tensor Analysis. McGraw Hill Book Company, Inc. pp. 71–77.
^ ^a ^b ^c Torge, Wolfgang (2001). Geodesy. ISBN 9783110170726.
^ ^a ^b ^c Moritz, H. (March 2000). "Geodetic Reference System 1980". Journal of Geodesy. 74 (1): 128–133. Bibcode:2000JGeod..74..128.. doi:10.1007/s001900050278. S2CID 195290884.
^ ^a ^b 스나이더, J.P.(1987년)지도 예측 – 작업 매뉴얼(미국 지질조사 전문가용 문서 1395) 페이지 16-17.워싱턴 D.C: 미국 정부 인쇄국.
^ ^a ^b ^c "Discover-TheWorld.com – Guam – POINTS OF INTEREST – Don't Miss – Mariana Trench". Guam.discover-theworld.com. 1960-01-23. Archived from the original on 2012-09-10. Retrieved 2013-09-16.
^ ^a ^b Frédéric Chambat; Bernard Valette (2001). "Mean radius, mass, and inertia for reference Earth models" (PDF). Physics of the Earth and Planetary Interiors. 124 (3–4): 234–253. Bibcode:2001PEPI..124..237C. doi:10.1016/S0031-9201(01)00200-X. Archived from the original (PDF) on 30 July 2020. Retrieved 18 November 2017.
^ Williams, David R. (2004-09-01), Earth Fact Sheet, NASA, retrieved 2007-03-17
^ Phillips, Warren (2004). Mechanics of Flight. John Wiley & Sons, Inc. p. 923. ISBN 0471334588.
^ Aristotle. On the Heavens. Vol. Book II 298 B. Retrieved 5 November 2017.
^ Drummond, William (1817). "On the Science of the Egyptians and Chaldeans, Part I". The Classical Journal. 16: 159.
^ Clarke, Alexander Ross; Helmert, Friedrich Robert (1911). "Earth, Figure of the" . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 8 (11th ed.). Cambridge University Press. pp. 801–813.
^ "Eratosthenes, the Greek Scientist". Britannica.com. 2016.

외부 링크

Merrifield, Michael R. (2010). " $R_{\oplus }$ The Earth's Radius (and exoplanets)". Sixty Symbols. Brady Haran for the University of Nottingham.

[3] 자세한 내용은 지구, 지오이드 및 지구 조수의 수치를 참조하십시오.

[4] 지오이드에는 하나의 중심이 없으며 지역 측지 조건에 따라 달라집니다.

[5] 지구중심 타원체에서, 타원체의 중심은 지구의 계산된 중심과 일치하며, 지구 전체를 가장 잘 모델링합니다.측지 타원체는 지질의 지역적 특성에 더 적합하다.타원체의 일부 표면이 영역에 적합하며, 이 경우 타원체의 중심과 방향이 일반적으로 지구의 질량 중심이나 회전 축과 일치하지 않습니다.

[6] 반지름 값은 타원체 모델의 경우 위도에 따라 완전히 달라지며 지오이드에 따라 거의 달라집니다.

[8] 이는 국제천문연맹의 정의 규칙(2)에 따른 것이다.행성은 중력과 원심력이 거의 ^[3]균형을 이루는 정수적 평형에 의해 형태를 띠게 된다.

[curvprim-14] 동서 방향은 오해의 소지가 있습니다.A에서 정동으로 나타나는 점 B는 A보다 적도에 더 가까울 것이다.따라서 이 방법으로 발견된 곡률은 적도를 제외하고 일정한 위도의 원의 곡률보다 작습니다.이 논의에서는 서쪽과 동쪽을 교환할 수 있다.

[15] $N$ 은 특정 관심 지점의 타원체 표면과 자오선을 통과하는 평면에서의 곡률 반경으로 정의된다.

[IAU_XXIX-1] ^ ^a ^b ^c ^d ^e ^f Mamajek, E. E; Prsa, A; Torres, G; et al. (2015). "IAU 2015 Resolution B3 on Recommended Nominal Conversion Constants for Selected Solar and Planetary Properties". arXiv:1510.07674 [astro-ph.SR].

[Moritz-2] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j 모리츠, H. (1980년)1980년 캔버라에서 열린 IUG의 17I 총회 결의에 의한 측지 참조 시스템.

[7] IAU 2006 총회: IAU 결의안 투표 결과 2006-11-07년 웨이백 머신에 보관

[9] 2002년 8월 1일, 고다드 우주 비행 센터에서 인공위성이 지구 중력장의 큰 변화의 신비를 밝히고 있다.

[10] 2005년 12월 20일, 고다드 우주 비행 센터, 그린랜드가 더 빨리 녹는 것을 발견한 NASA의 그레이스.

[tr8350_2-11] ^ ^a ^b ^c ^d ^e ^f ^g ^h "WGS84RPT.tif:Corel PHOTO-PAINT" (PDF). Retrieved 2018-10-17.

[12] "Info" (PDF). earth-info.nga.mil. Archived from the original (PDF) on 2020-08-04. Retrieved 2008-12-31.

[13] "Equatorial Radius of the Earth". Numerical Standards for Fundamental Astronomy: Astronomical Constants : Current Best Estimates (CBEs). IAU Division I Working Group. 2012. Archived from the original on 2016-08-26. Retrieved 2016-08-10.

[Bowring-16] Bowring, B. R. (October 1987). "Notes on the curvature in the prime vertical section". Survey Review. 29 (226): 195–196. doi:10.1179/sre.1987.29.226.195.

[17] Bomford, G. (1952). Geodesy. OCLC 489193198.

[Lass-18] Lass, Harry (1950). Vector and Tensor Analysis. McGraw Hill Book Company, Inc. pp. 71–77.

[Torge-19] Torge, Wolfgang (2001). Geodesy. ISBN 9783110170726.

[Moritz2000-20] Moritz, H. (March 2000). "Geodetic Reference System 1980". Journal of Geodesy. 74 (1): 128–133. Bibcode:2000JGeod..74..128.. doi:10.1007/s001900050278. S2CID 195290884.

[Snyder_manual-21] 스나이더, J.P.(1987년)지도 예측 – 작업 매뉴얼(미국 지질조사 전문가용 문서 1395) 페이지 16-17.워싱턴 D.C: 미국 정부 인쇄국.

[extrema-22] "Discover-TheWorld.com – Guam – POINTS OF INTEREST – Don't Miss – Mariana Trench". Guam.discover-theworld.com. 1960-01-23. Archived from the original on 2012-09-10. Retrieved 2013-09-16.

[chambat-23] Frédéric Chambat; Bernard Valette (2001). "Mean radius, mass, and inertia for reference Earth models" (PDF). Physics of the Earth and Planetary Interiors. 124 (3–4): 234–253. Bibcode:2001PEPI..124..237C. doi:10.1016/S0031-9201(01)00200-X. Archived from the original (PDF) on 30 July 2020. Retrieved 18 November 2017.

[earth_fact_sheet-24] Williams, David R. (2004-09-01), Earth Fact Sheet, NASA, retrieved 2007-03-17

[Phillips-25] Phillips, Warren (2004). Mechanics of Flight. John Wiley & Sons, Inc. p. 923. ISBN 0471334588.

[26] Aristotle. On the Heavens. Vol. Book II 298 B. Retrieved 5 November 2017.

[27] Drummond, William (1817). "On the Science of the Egyptians and Chaldeans, Part I". The Classical Journal. 16: 159.

[28] Clarke, Alexander Ross; Helmert, Friedrich Robert (1911). "Earth, Figure of the" . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 8 (11th ed.). Cambridge University Press. pp. 801–813.

[29] "Eratosthenes, the Greek Scientist". Britannica.com. 2016.

[1]

[2]

[a]

[b]

[c]

[d]

[e]

[4]

[5]

[6]

[7]

[8]

[f]

[g]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[3]

v t 천문학에서 사용되는 길이의 단위
천문 단위계
접지 반지름(`R`_Earth 또는_E R) 광초(ls) 태양 반지름(`R`）_☉ 。 기가미터(Gm) 천문 단위(au) 테라메터(Tm) 광년(ly) parsec (pc) 킬로파섹(kpc) 메가파섹(Mpc) 기가파섹(Gpc)
「」를 참조해 주세요. 우주 거리 사다리 크기 순서(길이) 유닛의 변환

Search

지구 반지름

네임스페이스

더

목차

서론

지구 변형의 물리학

반지름 및 로컬 조건

극지점: 적도 및 극지름

위치 의존 반지름

지심 반지름

곡률 반지름

곡률의 주반경

자릿수

프라임 수직

극지 및 적도 곡률 반지름

파생

복합 곡률 반지름

방위각

비방향성

전역 반지름

공칭 반지름

산술 평균 반지름

오토할라 반지름

체적 반지름

정류 반지름

지형 반지름

지형적 극한

지형적 전역 평균

파생 수량: 지름, 원주, 호 길이, 면적, 부피

공개된 값

역사

「」를 참조해 주세요.

메모들

레퍼런스

외부 링크

Search

지구 반지름

서론

지구 변형의 물리학

반지름 및 로컬 조건

극지점: 적도 및 극지름

위치 의존 반지름

지심 반지름

곡률 반지름

곡률의 주반경

자릿수

프라임 수직

극지 및 적도 곡률 반지름

파생

복합 곡률 반지름

방위각

비방향성

전역 반지름

공칭 반지름

산술 평균 반지름

오토할라 반지름

체적 반지름

정류 반지름

지형 반지름

지형적 극한

지형적 전역 평균

파생 수량: 지름, 원주, 호 길이, 면적, 부피

공개된 값

역사

「 」를 참조해 주세요.

메모들

레퍼런스

외부 링크

「」를 참조해 주세요.