등각 투영법

시리즈의 일부
그래피컬
평면 평행 투영 맞춤법 투영법 등각 투영법 경사 투영 투시 투영 곡선 원근법 역시점
표시 조감도 횡단면 컷어웨이 도면 분해도 어안 렌즈 멀티뷰 파노라마 웜 아이 뷰 줌 렌즈
토픽 3D 투영 무지외반증 축삭계 컴퓨터 그래픽스 컴퓨터 지원 설계 기술 기하학 엔지니어링 도면 지도 투영 그림 평면 계획(도면) 투영(선형 대수) 투영 평면 투영 형상 입체경 검사 기술 도면 참길이 소실점 비디오 게임 그래픽스 좌절을 표시
v t

Isometric Projection은 3차원 객체를 2차원으로 시각적으로 기술 및 엔지니어링 도면에서 표현하는 방법입니다.이것은 세 개의 좌표 축이 동일하게 단축되어 보이고 둘 사이의 각도가 120도인 축도 투영법입니다.

개요

"등각도"라는 용어는 그리스어로 "균등도"를 의미하며, 이는 투영의 각 축을 따른 척도가 (다른 형태의 그래픽 투영과 달리) 동일하다는 것을 반영한다.

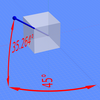
x, y, zaxes의 돌기 사이의 각도가 모두 같거나 120°가 되도록 시야 방향을 선택함으로써 물체의 등각도를 얻을 수 있다.예를 들어, 큐브를 사용할 때, 이것은 먼저 한 면을 정면으로 바라봄으로써 이루어집니다.다음으로, 입방체를 수직 축을 중심으로 ±45° 회전시킨 후 약 35.264° 회전시킨다(정확한 아크신).1al3 또는 arctan 1√2로, 이는 수평축에 대한 매직 각도와 관련이 있습니다.입방체(이미지 참조)를 사용하면 결과 2D 도면의 둘레는 완벽한 정육각형입니다. 즉, 검은색 선의 길이는 같고 입방체의 면은 모두 동일합니다.Isometric 그래프 용지를 일반 도화지 아래에 두면 계산 없이 효과를 얻을 수 있습니다.

마찬가지로 3D 장면에서도 등각 뷰를 얻을 수 있습니다.카메라가 바닥과 평행하게 정렬되고 좌표축에 정렬된 상태에서 위와 같이 먼저 약 35.264° 수직(수평축 주위로) 회전한 다음 수직축 주위로 ±45° 회전합니다.

등각 투영을 시각화할 수 있는 또 다른 방법은 위쪽 모서리에서 시작하여 반대쪽 아래 모서리 쪽을 보는 것입니다.x축은 대각선 아래 및 오른쪽으로, y축은 대각선 아래 및 왼쪽으로, z축은 위로 직진합니다.깊이는 이미지의 높이로도 표시됩니다.축을 따라 그려진 선은 서로 120°입니다.

이 모든 경우, 모든 축삭측정 및 맞춤 투영과 마찬가지로, 이러한 카메라는 카메라로부터의 거리에 따라 투영 길이가 변하지 않도록 물체-공간 텔레센트릭 렌즈가 필요합니다.

"등각도"라는 용어는 일반적으로 축삭 투영을 가리키는 데 잘못 사용되는 경우가 많습니다.그러나 축삭 투영에는 실제로 등각도, 치수도, 경사도 등 세 가지 유형이 있습니다.

회전각

등각 투영에 필요한 두 가지 각도에서 두 번째 값은 직관에 반하는 것처럼 보일 수 있으므로 좀 더 자세히 설명할 필요가 있습니다.먼저 길이가 2인 변과 그 중심이 축 원점에서 1의 거리에서 모든 면이 축과 교차하는 입방체를 상상해 보겠습니다.우리는 피타고라스의 정리를 사용하여 중심에서 가장자리 중간까지의 선의 길이를 θ2로 계산할 수 있습니다. 따라서 x축에서 입방체를 45° 회전시킴으로써 점(1, 1, 1)은 그림과 같이 (1, 0, θ2)이 됩니다.두 번째 회전은 양의 z축에 동일한 점을 가져오는 것을 목표로 하므로 1µ22의 아크탄젠트(약 35.264°)와 동일한 값의 회전을 수행해야 합니다.

수학

뷰어가 어느 8진수로 보이는지에 따라 등각도를 얻기 위한 8가지 방향이 있습니다.첫 번째 8진수를 들여다보는 3D 공간의 점_x,y,z a에서 2D 공간의 점_x,y b로의 등각 변환은 다음과 같이 회전 행렬을 사용하여 수학적으로 작성할 수 있습니다.

${\displaystyle{\begin{bmatrix}\mathbf{c}_{)}\\\mathbf{c}_{y}\\\mathbf{c}_{z}\\\end{bmatrix}}={\begin{bmatrix}1&, 0&, 0\\0&,{\cos \alpha}&,{\sin \alpha}\\0&,{-\sin \alpha}&,{\cos \alpha}\\\end{bmatrix}}{\begin{bmatrix}{\cos \beta}&, 0&,{-\sin \beta}\\0&, 1&, 0\\{\sin \beta}&, 0&,{\cos \beta}\\\end{bmatrix.}}{\begin{bmatrix}\mathbf{를}_{)}\\\mathbf{를}_{y}\\mathbf {a}_{z}\\end{bmatrix}=sublac {1}{\sublicrt {6}}{\sublicrt {3}}{\sublicrt {3}}\1&1\{\sublict {\rt}}}{\sublict {\sublict}}{{{{bmat}}}}}}}{{{{\sublict}}}}}}}}}}{{{\sublac}}}}$

여기서 α = 아크신(탄 30°)θ 35.264° 및 β = 45°위에서 설명한 바와 같이, 이것은 β에 의해 수직(여기서 y) 축을 중심으로 한 회전이며, 이어서 수평(여기서 x) 축을 중심으로 한 회전이다.그런 다음 xy 평면에 대한 맞춤 투영을 수행합니다.

${\displaystyle {\mathbf {b} _{x} \\mathbf {b} _{y} \\\\end {bmatrix} = scap {bmatrix} 1 & 0 & 0 & 1 & 0 & 0 & 0 \ \ \ \ \ \ \ \ \ \ \ 0 matrix } { bmatrix } { b}$

다른 7가지 가능성은 반대 방향으로 회전하거나 회전하지 않고 뷰 방향을 반전하거나 ^[1]반전하지 않음으로써 얻을 수 있습니다.

이력 및 제한 사항

William Farish 교수 (1759–1837)에 의해 처음 공식화된 등각계의 개념은 ^[3][4]수세기 동안 대략적인 경험적 형태로 존재해 왔다.19세기 중반부터 등각계는 엔지니어들에게 가치 없는 도구가 됐고 곧 유럽과 ^[5]미국의 건축교육 과정에 축삭측정법과 등각법이 도입됐다.^[6]중국 미술에서 그것의 기능은 유럽 미술의 선형 원근법과 유사했다.Axonometry와 그에 따른 그림 문법은 비주얼 컴퓨팅의 등장으로 새로운 의미를 갖게 되었습니다.^[6]

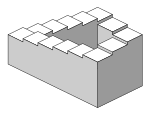
모든 유형의 평행 투영과 마찬가지로 등각 투영으로 그려진 개체는 뷰어에 더 가깝거나 더 멀리 확장될 때 더 크거나 더 작아 보이지 않습니다.측정을 직접 수행해야 하는 건축 도면에는 유리하지만, 투시 투영과 달리 인간의 시각이나 사진이 일반적으로 작동하는 방식이 아니기 때문에 왜곡이 인지됩니다.또한 오른쪽 그림과 같이 깊이와 고도를 측정하기 어려운 상황에서도 쉽게 발생할 수 있습니다.이것은 펜로즈 계단처럼 역설적이거나 불가능한 모양을 만드는 것처럼 보일 수 있다.

비디오 게임 및 픽셀 아트에서의 사용

등각 비디오 게임 그래픽은 비디오 게임과 픽셀 아트에 채용된 그래픽으로 평행 투영을 이용하지만, 하향식 관점이나 측면 뷰에서는 보이지 않는 환경의 면을 보여주기 위해 시점을 조정하여 입체감을 준다.이름에도 불구하고 등각 컴퓨터 그래픽이 반드시 등각선일 필요는 없습니다.즉, x, y 및 z축이 서로 120° 방향을 향하고 있는 것은 아닙니다.대신 다양한 각도가 사용되며, 치수 투영과 2:1 픽셀 비율이 가장 일반적입니다."3⁄4 perspective", "3⁄4 view", "2.5D" 및 "pseudo 3D"라는 용어도 가끔 사용되지만, 이러한 용어가 다른 맥락에서 약간 다른 의미를 가질 수 있다.

이전에는 보다 강력한 3D 그래픽 시스템이 등장하면서 등각 투영법이 보편화되었고, 비디오 게임이 액션과 ^[7]개별 캐릭터에 더욱 초점을 맞추기 시작했습니다.그러나 등각 투영법을 이용한 비디오 게임, 특히 컴퓨터 롤플레잉 게임은 인디 게임 분야에서 ^[7][8]최근 몇 년간 부활하고 있습니다.

「 」를 참조해 주세요.

• 그래피컬

레퍼런스

외부 링크

• 등각 투영