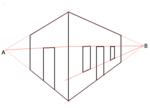
소실점

Vanishing point
다른 용도는 소실점(동음이의)을 참조하십시오.
이 철도의 저 끝에 소실점이 보인다

소실점은 투시도 상의 3차원 공간에서의 서로 평행한 선의 2차원 투시 투시 투시가 수렴하는 것처럼 보이는 점이다.평행선 세트가 그림 평면에 수직인 경우 구조를 원포인트 투시라고 하며, 소실점은 이미지를 올바른 투시 [1]형상으로 표시해야 하는 안구 또는 "안구"에 해당합니다.기존의 선형 도면에서는 1~3개의 평행선이 있는 객체를 사용하여 1~3개의 소실점을 정의합니다.

시리즈의 일부
그래피컬
Axonometric projection.svg
평면
표시
토픽

이탈리아의 인문주의자인 박식가이자 건축가 레온 바티스타 알베르티는 [2]1435년에 쓰여진 원근법에 대한 그의 논문에서 이 개념을 처음 도입했다.

벡터 표기법

소실점 형성을 보여주는 투시 2차원 구성

소실점은 방향 벡터(예: D)가 동일한 선이 동일한 소실점을 가지므로 "방향점"이라고도 할 수 있습니다.수학적으로, q ≡(x, y, f) 순간이 어디 f는 초점 거리(카메라에서 이미지와 관련된)이미지를 비행기에 누워 있고, vq({.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion ≡ 보겠습니다.디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{.국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}x/h, y/h, f/h)이 단위 벡터 q와 관련된, h)√x2+y2+f2.공간 S의 단위x 벡터s n δy(nz, n, n)와 그 소실점s v를 갖는 직선을 고려하면 v와s 관련된 단위 벡터는 두 점이 모두 영상 [3]평면을 향한다고 가정할 때 n과 같다s.

영상 평면이 두 개의 월드 좌표 축에 평행한 경우 이 영상 평면에 의해 절단된 축과 평행한 선에는 단일 소실점에서 만나는 영상이 있습니다.다른 두 축에 평행한 선은 영상 평면에 평행하므로 소실점을 형성하지 않습니다.이것은 원포인트 시점입니다.마찬가지로 이미지 평면이 두 개의 월드 좌표 축과 교차할 때 이러한 평면에 평행한 선은 이미지 평면에서 두 개의 소실점을 형성합니다.이를 2점 시점이라고 합니다.3점 관점에서는 영상 평면이 x, y 및 z 축과 교차하므로 이러한 축에 평행한 선이 교차하여 세 개의 서로 다른 소실점이 발생합니다.

정리

소실점 정리는 원근법의 주요 정리이다.화상과 평행하지 않은 공간에서의 선 L의 화상 평면 θ 내의 화상은 θ와의 교집합과 소실점에 의해 결정된다고 한다.일부 저자들은 "선의 이미지는 소실점을 포함한다"라는 문구를 사용했다.Guidobaldo del Monte는 몇 가지 검증을 했고, Humphry Ditton은 그 결과를 "주요하고 위대한 제안"[4]이라고 불렀다.브룩 테일러는 1714년에 원근법에 관한 첫 번째 책을 썼는데, 이 책은 "소실점"이라는 용어를 도입하여 다점 원근법의 기하학적 구조를 가장 먼저 설명했고, 역사가 커스티 안데르센이 이러한 [1]: 244–6 관찰들을 정리했다.그녀는 투영 기하학의 관점에서 소실점은 O에서 소실점을 통과하는 시선이 L과 평행하기 때문에 L과 연관된 무한대의 점의 이미지라고 지적한다.

소실선

소실점은 선에서 시작되므로 소실선은 화상θ와 평행하지 않은 평면α에서 발생한다.α에 평행하고 O상에 놓여 있는 평면 O와 β가 주어졌을 때 α의 소실선은 βθθ이다.예를 들어, α가 지면이고 β가 수평면일 때, α의 소실선은 수평선 β θ θ이다. Anderson은 "특정 소실선은 한 개만 발생하며, 종종 "수평선"[1]: 249, 503–6 이라고 한다"고 지적한다.

간단히 말하면, 어떤 면의 소실선, 예를 들면 α는, 카메라 중심을 통과하는 다른 면, 예를 들면 β와 다른 면의 교점에 의해서 얻을 수 있다.이 평면α에 평행한 다른 선 세트에 대해 각각의 소실점은 이 소실선상에 놓인다.수평선은 관찰자의 눈높이를 나타내는 이론적인 선입니다.물체가 수평선 아래에 있는 경우, 사라지는 선은 수평선까지 각도를 조정합니다.물체가 위에 있으면 아래로 기울어집니다.모든 소실선은 수평선에서 끝난다.

소실점의 특성

(가) 어떤 평면 θ에A 놓여 있는 두 쌍의 평행선의 투영, 즉 그 쌍과 관련된 소실점이 수평선 또는 θ에A 평행한 평면과 핀홀을 통과하는 화상평면의 교점에 의해 형성된 소실선 H에 수렴하는 것으로 보인다.실증:그라운드 평면 θ를 y = c로 간주합니다. 즉, 단순성을 위해 영상 평면에 직교합니다.또한 평면 θ에 있는 선 L을 고려합니다. 이 선은 ax + bz = d라는 방정식으로 정의됩니다. 원근 핀홀 투영을 사용하여 이미지 평면에 투영된 L 위의 점은 다음과 같이 좌표가 정의됩니다.

x440 = f·x/z = f·d - bz/az
y440 = f·y/z = f·c/z

z를 파라미터로 하여 라인 L의 이미지 L†을 파라미터로 표현한 것입니다.z → -discloss이면 영상 평면의 xisclosis 축에 있는 점(xiscl,yisclos) =(-fb/a,0)에서 멈춥니다.평면θ의 기울기가 -b/a인 모든 평행선에 대응하는 소실점입니다.평면 θ에 속하는 다른 기울기를 가진 다른 선과 관련된 모든 소실점은 x' 축에 놓입니다. 이 경우 수평선이 됩니다.

(2) A, B, C를 공간상 서로 직교하는 3개의 직선으로 하고, v θA(xA, yA, f), v θBC(xB, yB, f), v θ(xC, yC, f)를 각각 대응하는 3개의 소실점으로 한다.이 점들 중 하나의 좌표, 예를 들어AB v와 두 번째 점을 통과하는 이미지 평면의 직선 방향을 알면 v와C v의B 좌표를 모두 계산할 수 있습니다.

3. A, B, C를 공간상 상호 직교하는 3개의 직선으로 하고A, v θ(xAB, yA, f), v θ(xB, yB, f), vC θ(xC, yC, f)를 각각 대응하는 3개의 소실점으로 한다.세 개의 소실점에 정점이 있는 삼각형의 직교점은 광축과 영상 [3]평면의 교차점입니다.

곡선 및 역원근법

곡선 원근법은 소실점이 4개 또는 5개인 도면입니다.5점 시야에서 소실점은 N, W, S, E의 주요 표제에 4개의 소실점과 원의 원점에 1개의 소실점을 가진 원으로 매핑된다.

반대 원근법은 그림 바깥쪽에 마치 그림 앞에 있는 것처럼 보이는 소실점이 있는 그림이다.

소실점 검출

소실점 검출을 위한 몇 가지 방법은 영상에서 검출된 선분을 사용합니다.다른 기법으로는 영상 픽셀의 명암 구배를 직접 고려해야 합니다.

이미지에는 상당히 많은 소실점이 존재합니다.따라서 씬(scene)의 주요 방향에 해당하는 소실점을 검출하는 것이 목적입니다.이것은 보통 두 단계로 이루어집니다.이름에서 알 수 있듯이 누적 단계라고 하는 첫 번째 단계에서는 군집이 공통 소실점을 갖는다는 가정 하에 선분을 군집화합니다.다음 단계에서는 씬(scene)에 있는 주 클러스터를 찾기 때문에 검색 단계라고 합니다.

축적 스텝에서는, 화상을 축적 공간이라고 불리는 경계 공간에 매핑 한다.축전지 공간은 셀이라고 불리는 단위로 분할됩니다.Barnard는 이 공간을 카메라의 광중심을 중심으로 한 가우스 구면(Gaussian spole)으로 축전지 공간으로 가정했다.화상상의 선분은, 이 구상의 대원에 대응해, 화상내의 소실점은 점에 매핑된다.가우스 구에는 거대한 원이 셀을 통과할 때 증가하는 축전지 셀이 있습니다. 즉, 이미지에서 선분이 소실점과 교차합니다.이후 몇 가지 수정이 이루어졌지만, 가장 효율적인 기술 중 하나는 선분의 매개변수를 경계 공간에 매핑하는 Hough Transform(Hough Transform(호프 변환)을 사용하는 것이었습니다.캐스케이드 하프 변환이 여러 소실점에 적용되었습니다.

영상에서 경계 공간으로 매핑하는 프로세스로 인해 선 세그먼트와 점 사이의 실제 거리가 손실됩니다.

서치 스텝에서는, 그것을 통과하는 회선 세그먼트의 최대수를 가지는 어큐뮬레이터 셀을 요구한다.그런 다음 해당 선분을 제거하고 이 카운트가 특정 임계값을 밑돌 때까지 검색 단계를 반복합니다.컴퓨팅 능력이 향상됨에 따라 상호 직교하는 두 세 방향에 해당하는 점을 찾을 수 있습니다.

소실점 적용

투영 기하학에서 교차 비율을 사용하여 투시 투영에서 묘사된 피쳐의 실제 치수를 측정합니다.A, B, C, D 및 V는 이미지 상의 점이며, 픽셀 단위로 구분됩니다. A', B', C' 및 D'는 실제 세계에서 미터 단위로 구분됩니다.
  • (1)에서는 인접한 점포의 기존 폭에서 샛길 폭 W를 산출한다.
  • (2)에서는 소실점 V가 보이기 때문에 1개 점포의 폭만 있으면 된다.
  1. 카메라 보정:영상의 소실점에는 카메라 보정에 필요한 중요한 정보가 포함되어 있습니다.소실점의 특성을 사용하여 내적 및 외적 교정 파라미터를 [6]찾는 다양한 교정 기법이 도입되었습니다.
  2. 3D 재구성:인공 환경은 씬(scene)의 여러 선이 평행하고 존재하는 여러 가장자리가 직교하는 두 가지 주요 특성을 가집니다.소실점은 환경을 이해하는 데 도움이 된다.평면의 평행선 세트를 사용하여 소실점을 사용하여 평면의 방향을 계산할 수 있습니다.Torre와 Coelho는[8] 전체 시스템을 구현하기 위해 소실점을 사용하는 광범위한 조사를 수행했다.환경이 레고랜드라고도 불리는 평행하거나 수직인 면만을 가진 물체로 구성되어 있다는 가정 하에, 그들은 장면의 단일 이미지에 만들어진 소실점을 사용하여 장면의 3D 형상을 복구했습니다.로봇 공학 분야에서도 유사한 아이디어가 사용되고 있는데, 주로 내비게이션과 무인 자동차 분야, 물체 탐지와 관련된 분야에서도 사용되고 있다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ a b c Kirsti Andersen (2007) 예술의 기하학, 페이지 xxx, Springer, ISBN0-387-25961-9
  2. ^ Wright, D. R. Edward (1984). "Alberti's De Pictura: Its Literary Structure and Purpose". Journal of the Warburg and Courtauld Institutes. 47: 52–71. JSTOR 751438.
  3. ^ a b c 카프릴, 브이Torre [1] "카메라 보정을 위한 소실점 사용", 국제 컴퓨터 비전 저널, 제4권, 제2호, 127-139페이지, 1990년 3월
  4. ^ H. Ditton (1712) 원근법에 관한 논문, 페이지 45
  5. ^ S.T. Barnard '투시 이미지 해석', 인공지능 21, 1983, 페이지 435 - 462
  6. ^ D. Liebowitz와 A.지서만 "평면의 투시 이미지를 위한 미터법 정류", IEEE Conf.컴퓨터 비전과 패턴 인식, 1998년 6월, 캘리포니아주 산타바바라, 페이지 482-488
  7. ^ R.T. 콜린스, R.ICCV3의 Weiss "단위구간에 대한 통계적 추론으로서의 소멸점 계산" 절차, 1990년 12월
  8. ^ C. Coelho, M. Straforani, M. Campani "실내 경치의 이해를 위한 기하학적 규칙과 선험적 지식의 사용" 절차 BMVC90, 페이지 229-234 옥스퍼드, 1990년 9월.

외부 링크