경사 투영

이 기사의 리드 섹션이 너무 짧아서 요점을 적절하게 요약할 수 없을 수 있습니다. 기사의 모든 중요한 측면에 대한 접근 가능한 개요를 제공하기 위해 잠재 고객을 확대하는 것을 고려해 주십시오. (2015년 2월)

이 문서에서는 3D 객체의 이미징에 대해 설명합니다.추상적인 수학적 설명은 투영(선형 대수)을 참조하십시오.

시리즈의 일부
그래피컬
평면 평행 투영 맞춤법 투영법 등각 투영법 경사 투영 투시 투영 곡선 원근법 역시점
표시 조감도 횡단면 컷어웨이 도면 분해도 어안 렌즈 멀티뷰 파노라마 웜 아이 뷰 줌 렌즈
토픽 3D 투영 무지외반증 축삭계 컴퓨터 그래픽스 컴퓨터 지원 설계 기술 기하학 엔지니어링 도면 지도 투영 그림 평면 계획(도면) 투영(선형 대수) 투영 평면 투영 형상 입체경 검사 기술 도면 참길이 소실점 비디오 게임 그래픽스 좌절을 표시
v t

경사 투영법은 3차원(3D) 객체의 2차원(2D) 이미지를 생성하는 데 사용되는 그래픽 투영 기술의 단순한 유형입니다.

오브젝트는 원근법에 맞지 않기 때문에 실제로 얻을 수 있는 오브젝트의 뷰에 대응하지 않지만, 이 기술은 어느 정도 설득력 있고 도움이 됩니다.

경사 투영법은 기술 도면에서 일반적으로 사용됩니다.카발리에 투영은 18세기 프랑스 군사 예술가들이 요새를 묘사하기 위해 사용되었습니다.

사선투영은 1세기 또는 2세기부터 18세기까지 중국 예술가들에 의해 거의 보편적으로 사용되었으며,^[1] 특히 집과 같은 직선적인 물체를 묘사하기 위해 사용되었다.

CAD(컴퓨터 지원 설계), 컴퓨터 게임, 컴퓨터 생성 애니메이션, 영화 특수 효과 등 다양한 그래픽 투영 기술을 컴퓨터 그래픽에 사용할 수 있습니다.

개요

경사 투영법은 평행 투영법의 한 종류입니다.

• 평행선(프로젝터)을 교차시켜 이미지를 투영합니다.
• 도면 표면이 있는 3차원 소스 객체(투영 평면)에서 추출합니다.

경사 투영과 직교 투영 모두에서 소스 객체의 평행선은 투영된 영상에 평행선을 생성합니다.사선 투영의 프로젝터는 사선 각도로 투영 평면을 교차하여 투영된 이미지를 생성합니다. 이는 직교 투영에 사용되는 수직 각도와는 반대입니다.

수학적으로 $(\displaystyle$ xy$}$ $평면상$의 점$({\displaystyle x,}$ $)$ {$displaystyle(x, y,z)}$의 평행 투영에 의해${\displaystyle }$(${\displaystyle x}$ ${\displaystyle +}$ ${\displaystyle a}$ ${\displaystyle z,y}$ + ${\displaystyle b}$z, $)$ {$displaystyle(x+az,y+bz,0$이 표시됩니다.a$(\displaystyle$ a$$$)$ $및{\displaystyle }$ b$(\displaystyle$ b$)$ $상수$는 병렬 투영을 고유하게 지정합니다.a ${\displaystyle =}$ ${\displaystyle b}$ ${\displaystyle =}$ {$style$ a$=b=0$일 때, 투영은 "직교" 또는 "직교"라고 합니다.그렇지 않으면 "oblique"입니다.$a(\$displaystyle $a)$와 b$(\displaystyle$ b$)$의 $상수$는 반드시 1보다 작을 필요는 없으며, 그 결과 비스듬한 투영으로 측정되는 길이는 우주에서 측정되던 길이보다 크거나 짧을 수 있습니다.일반적인 사선 투영에서는 공간의 구가 직교 투영에서 나타나는 원이 아니라 도면 평면에 타원형으로 투영됩니다.

사선 드로잉은 또한 가장 조잡한 "3D" 드로잉 방식이지만 마스터하기 가장 쉽습니다.비스듬한 뷰를 사용하여 그리는 한 가지 방법은 보고 있는 물체의 측면을 2차원으로 그린 다음 다른 면을 45°의 각도로 그리는 것입니다. 그러나 이 측면은 풀사이즈로 그리는 것이 아니라 '강제 깊이'를 만드는 절반 깊이만 그려서 물체에 사실적인 요소를 추가합니다.이런 '강제심도'에도 불구하고, 사선 그림은 보기에 매우 설득력이 없어 보인다.이러한 이유로 사선은 전문 디자이너나 엔지니어가 거의 사용하지 않습니다.

사선화보

사선도면에서는 축간에 표시되는 각도와 전단률(척도)이 임의이다.보다 정확하게는, 같은 점으로부터 시작되는 3개의 코프라 세그먼트(segment)의 소정의 집합은, 큐브의 3개의 변의 사선 투시를 형성하고 있는 것으로 해석할 수 있다.이 결과는 독일 ^[2]수학자 폴케가 19세기 초에 발표한 폴케의 정리라고 알려져 있다.

그 결과 왜곡으로 인해 기법은 정식 작업 도면에 적합하지 않습니다.단, 화상의 한쪽 평면을 투영면에 평행하게 함으로써 왜곡을 부분적으로 극복한다.이렇게 하면 선택한 평면의 실제 모양 이미지가 생성됩니다.이 사선 투영의 특정 범주는 x$(\displaystyle$x) $및$ y(\$displaystyle$ y$)$ $방향$의 길이는 보존되지만 z$(\displaystyle$ z$)$ $방향$의 길이는 축소 계수를 사용하여 각도로 그려진다.

• Cavalier projection은 이러한 $투영법$의 이름으로$,$ z\$displaystyle$z 축을$$ 따라 있는 길이가 ^[3]스케일링되지 않은 상태로 유지됩니다.
• 가구 일러스트에서 널리 사용되는 캐비닛 투영법은 후퇴하는 축을 절반 크기^[3](때로는 ^[4]원본의 3분의 2 크기)로 축척하는 기술의 한 예입니다.

카발리에 투영법

카발리어 투영(카발리어 투시 또는 하이 뷰 포인트)에서 객체의 점은 x, y 및 z의 세 가지 좌표로 표시됩니다.도면에 x and와 y″ 두 개의 좌표만으로 표시됩니다.평면도에서는 그림상의 2개의 축 x와 z가 수직이며, 이들 축의 길이는 1:1 축척으로 그려집니다.따라서 세 번째 축 y는 대각선으로 그려지며, 보통 30° 또는 45°의 X축과 임의의 각도를 형성하기 때문에 축척 투영과 유사합니다.세 번째 축의 길이는 ^[5][6]축척되지 않습니다.

그것은 특히 펜과 종이로 그리기가 매우 쉽다.따라서 칠판(강습, 구술 시험 등)에 손으로 그림을 그려야 할 때 자주 사용됩니다.

그 표현은 처음에는 군사 요새화에 사용되었다.프랑스어로 카발리에(cavalier, 말 그대로 기수, 기병 참조)는 성벽 뒤에 있는 인공 언덕으로 ^[7]성벽 위의 적을 볼 수 있게 해줍니다.기만적인 관점은 이 고지에서 사물을 보는 방식이었다.어떤 사람들은 말에서 ^[8]땅에 있는 작은 물체를 볼 수 있다는 사실로 그 이름을 설명하기도 한다.

캐비닛 투영

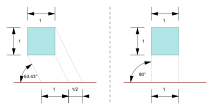
캐비닛 프로젝션이라는 용어는 ^[9]가구업계의 일러스트에 사용된 것에서 유래합니다.투사된 물체의 한쪽 면이 보기 평면에 평행하고 세 번째 축이 각도로 투영됩니다(일반적으로).atan(2) 또는 약 63.4°.세 번째 축이 길이를 유지하는 캐벌리어 투영과 달리 캐비닛 투영에서는 후퇴하는 선의 길이가 반으로 잘립니다.

수학 공식

공식으로 뷰어에 면한 평면이 xy이고 후퇴축이 z일 경우 점 P는 다음과 같이 투영됩니다.

$\displaystyle P{\begin{pmatrix}x\y\\z\end{pmatrix}=\begin{pmatrix}x+{\frac{1}{2}z\sin\alpha\0\end{pmatrix}}$

$여기$서$$α(\$displaystyle \alpha)$는 언급된 각도입니다.

변환 매트릭스는 다음과 같습니다.

$\displaystyle P=begin{bmatrix}1&{\frac {1}{2}\cos \alpha \\0&1&{\frac {1}{2}}\sin \alpha \\0&0&0\end{bmatrix}}$

또는 출발면에서 돌출된 리딩 암에서 1/3을 제거하여 동일한 결과를 얻을 수 있습니다.

군사 계획

밀리터리 투영에서는 x축과 z축의 각도와 y축과 z축의 각도가 45°이므로 x축과 y축의 각도는 90°이다.즉, xy 평면이 치우치지 않습니다.하지만 45° 이상 회전합니다.^[10]

예

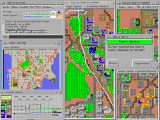
기술 드로잉과 일러스트 외에도 비디오 게임(특히 3D 게임의 등장 이전의 게임)은 사선 투영 형식을 사용하는 경우가 많습니다.예를 들어 SimCity, Ultima VII, Ultima Online, EarthBound, Paperboy, 최근에는 Tibia 등이 있습니다.

• 

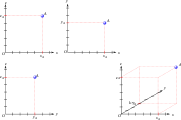
  왼쪽에 있는 그림은 맞춤법 투영법입니다.오른쪽에 있는 그림은 30°의 각도와 다음과 같은 비율을 가진 사선 투영입니다.1×2

• 

  45°의 각도와 2/3의 비율로 캐비닛 투영으로 그려진 화분 벤치.

• 

  기병의 관점에서 본 요새의 조각들 (Cyclopedia vol.1, 1728).

• 

  좌표를 어떻게 사용하여 기만적인 관점에 포인트를 배치하는지.

• 

  군사적 관점에서 그려진 돌 아치입니다.

• 

  캐비닛 원근법으로 그려진 돌 아치.

• 

  창덕궁과 창경궁 두 궁궐을 그린 대표적인 한국화입니다.

• 

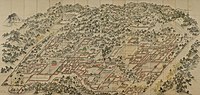
  야마의 입구, 마당.건륭제(建龍帝)가 명한 쉬양(徐陽)의 쑤저우(zhou州)에 관한 두루마리 상세. 18세기

• 

  군사 투영으로 그려진 18세기 포트 로열 데 샹의 계획

• 

  비디오 게임 SimCity에 밀리터리 프로젝션의 변형이 사용됩니다.

• 

  이상 쇄골하동맥을 구별하기 위해 비스듬한 투영으로 표시된 3D 렌더링 자기 공명 혈관 조영

「 」를 참조해 주세요.

• 공간 경사 메르카토르 투영
• 경사 메르카토르 투영법
• 요시다 하츠사부로
• 미술 기법 목록

레퍼런스

추가 정보

• Foley, James (1997). Computer Graphics. Boston: Addison-Wesley. ISBN 0-201-84840-6.
• Ingrid Carlbom, Joseph Paciorek, 평면 기하학적 투영 및 표시 변환, ACM Computing Surveies, v.10 n.4, 페이지 465~502, 1978년 12월
• Alpha 등 1988, Atlas of Oblique Maps, Atlas of Landform Rescripts of World(미국 지질조사국) 세계 일부 지역의 지형 묘사 모음

외부 링크

• 일러스트레이터 드래프트맨 3 & 2 – Volume 2 Standard Practices and Theory (제2권 표준 프랙티스와 이론), https://web.archive.org/web/20100822152816/http에서 68페이지