하트리-포크 방식

전자 구조 방법
발란스 본드 이론
콜슨-피셔 이론 일반화 발란스 본드 모던발란스 본드
분자 궤도 이론
하트리-포크 방식 반감기 양자화학법 뫼르-플레셋 섭동 이론 구성 상호 작용 커플링 클러스터 다중 구성 자체 일관성 필드 양자화학복합법 퀀텀 몬테 카를로
밀도함수이론
시간 의존적 밀도 기능 이론 토마스-페르미 모델 궤도무밀도기능이론
전자 밴드 구조
거의 자유 전자 모델 타이트 바인딩 머핀틴 근사치 k·p 섭동설 빈 격자 근사치
v t

컴퓨터 물리학 및 화학 분야에서는 하트리-Fock(HF) 방법은 정지 상태에서 파동함수와 양자 다체계의 에너지를 결정하기 위한 근사법이다.

하트리-Fock 방법은 종종 시스템의 정확한 N-body wave 기능이 단일 슬레이터 결정체(입자가 페르미온인 경우) 또는 N 스핀-오르비탈의 단일 영구(보손의 경우)에 의해 근사치될 수 있다고 가정한다.변동 방법을 호출함으로써 N 스핀 궤도에 대한 일련의 N 결합 방정식을 도출할 수 있다.이 방정식의 해법은 하트리-을 산출한다.Fock Wave 기능 및 시스템의 에너지.

특히 옛 문헌에서는 하트리-.포크 방식은 자기 일치 필드 방식(SCF)이라고도 한다.슈뢰딩거 방정식의 대략적인 해법으로서 현재 하트리 방정식이라고 불리는 것을 도출하면서, 하트리는 전하 분포로부터 계산된 최종 필드를 가정된 초기 영역과 "자체적으로 일치"하도록 요구하였다.그러므로 자기 일관성은 해결의 요구 사항이었다.비선형 하트리(Hartree)에 대한 해결책또한 Fock 방정식은 각 입자가 다른 모든 입자에 의해 생성된 평균 장에 따라 작용하는 것처럼 작용하며(아래 Fock 연산자 참조), 따라서 용어는 계속되었다.고정점 반복 알고리즘이 항상 수렴되는 것은 아니지만, 방정식은 거의 보편적으로 반복적인 방법을 통해 해결된다.^[1]이 솔루션 계획만이 가능한 것은 아니며 Hartree-의 필수적인 특징도 아니다.포크 방식.

하트리-Fock 방법은 원자, 분자, 나노구조체^[2] 및 고형물에 대한 Schrödinger 방정식의 용액에서 그것의 전형적인 용도를 찾지만, 그것은 또한 핵물리학에서도 널리 사용되는 것을 발견했다.(하트리- 참조)Fock-Bogolyubov의 핵구조 이론 적용에 대한 논의를 위한 방법).원자 구조 이론에서 계산은 흥분된 에너지 수준이 많은 스펙트럼에 대한 것일 수 있으며 결과적으로 Hartree–원자에 대한 fock 방법은 파동함수가 잘 정의된 양자수를 가진 단일 구성 상태 함수이며 에너지 수준이 반드시 접지 상태일 필요는 없다고 가정한다.

원자와 분자 모두에게 하트리-Fock 솔루션은 다전자를 보다 정확하게 설명하는 대부분의 방법의 중심 출발점이다.

이 글의 나머지 부분은 원자를 특수한 경우로 하는 분자에 적합한 전자 구조 이론의 응용에 초점을 맞출 것이다.여기서의 논의는 오직 제한된 하트리만을 위한 것이다.원자나 분자가 모든 궤도(원자 또는 분자)가 이중으로 점유된 폐쇄 쉘 시스템인 포크 방식.일부 전자가 쌍으로 구성되지 않은 오픈 쉘 시스템은 제한된 오픈 쉘 또는 무제한 하트리–로 처리될 수 있다.포크 방식.

간략한 역사

초기 반감기적 방법

하르트리의 기원-포크 방식은 1926년 슈뢰딩거 방정식이 발견된 직후인 1920년대 말로 거슬러 올라간다.더글러스 하트리의 방법은 1920년대 초의 일부 초기 반감광적인 방법들에 의해 안내되었다(E에 의해).Fues, R. B. Lindsay, 그리고 그 자신)은 보어의 옛 양자 이론을 배경으로 했다.

원자의 보어 모델에서 주 양자수 n을 가진 상태의 에너지는 $원자{\displaystyle }$ 단위로 E${\displaystyle }$=${\displaystyle }$- 1${\displaystyle }$/ ${\displaystyle n{}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$ 원자 스펙트럼으로부터 많은 전자 원자의 에너지 수준은 보어 공식의 변형판을 적용하여 잘 묘사되고 있음을 관찰하였다$.$양자결함 d를 경험적 매개변수로 도입함으로써 일반 원자의 에너지 수준은 X선 영역에서 관측된 전이 수준을 상당히 잘 재현할 수 있다는 점에서 ${\displaystyle {E\mathrm{}}^{}}$=${\displaystyle }$- 1${\displaystyle }$/${\displaystyle }$( ${\displaystyle n}$+ ${\displaystyle d{}^{}}$) 2 ${\$ E$=-1/(n+d)^{2}}$공식으로 잘 근사하게 추정되었다(예를 들어 경험적 d 참조).모슬리의 법칙에 반향과 파생이 있다.0이 아닌 양자 결함의 존재는 전자-전자 반발로 인해 발생했는데, 이는 격리된 수소 원자에는 분명히 존재하지 않는다.이러한 반발로 인해 원전의 일부만 선별되었다.이러한 초기 연구자들은 나중에 실험 데이터를 더 잘 재현할 수 있다는 희망을 가지고 추가적인 경험적 매개변수를 포함하는 다른 잠재력을 도입했다.

하트리법

1927년 D. R. 하트리는 원자나 이온에 대한 대략적인 파동함수와 에너지를 계산하기 위해 자기 일치장법이라고 하는 절차를 도입했다.^[3]하트리는 경험적 매개변수를 없애고 다체 시간 독립적 슈뢰딩거 방정식을 근본적인 물리적 원리, 즉 아비니티오에서 해결하려고 했다.그가 처음 제안한 해결방법은 하트리 방법, 즉 하트리 제품으로 알려지게 되었다.그러나 하트리의 동시대인들 중 다수는 하트리 방법의 물리적인 추리를 이해하지 못했는데, 그것은 많은 사람들에게 경험적 요소를 포함하는 것으로 나타났으며, 다체 슈뢰딩거 방정식의 해법과의 연관성은 불분명했다.그러나 1928년 J. C. Slater와 J. A. Gaunt는 독립적으로 단일 입자 함수의 산물로서 안사츠(trial wave function)에 변이 원리를 적용함으로써 하르트리의 방법을 음향기 이론적 기초에 따라 콜치할 수 있다는 것을 보여주었다.^[4][5]

1930년에 슬레이터와 V. A. Fock은 Hartree 방법이 파동함수의 비대칭 원리를 존중하지 않는다고 독자적으로 지적했다.^[6][7] 하트리 방법은 동일한 양자 상태에 두 전자가 존재하는 것을 금지하면서 이전 제형에서 파울리 배제 원칙을 사용했다.그러나 이는 양자통계를 소홀히 한 점에서 근본적으로 불완전한 것으로 나타났다.

하트리-포크

하르트리 방법의 반대칭성 결여에 대한 해결책은 1926년 하이젠베르크와 디라크에 의해 처음 사용된 단분위궤도의 결정인 슬레이터 결정요소가 정확한 용액의 대칭성 특성을 경미하게 만족하고 따라서 변동원리를 적용하기에 적합한 안사츠라는 것이 밝혀졌을 때 나왔다.원래의 Hartree 방법은 Hartree-에 대한 근사치로 볼 수 있다.교환을 소홀히 하여 Fock 메소드.포크의 원래 방법은 집단 이론에 크게 의존했고 현대 물리학자들이 이해하고 실행하기에는 너무 추상적이었다.1935년 하트리는 계산 목적에 더 적합하도록 방법을 개혁했다.^[8]

하트리-Fock 방법은, 물리적으로 더 정확한 그림에도 불구하고, 초기 Hartree 방법과 경험적 모델에 비해 훨씬 더 큰 계산적 요구 때문에 1950년대에 전자 컴퓨터가 등장하기 전까지 거의 사용되지 않았다.처음에는 하트리 방식과 하트리 방식 모두-fock 방법은 원자에 독점적으로 적용되었는데, 여기서 시스템의 구형 대칭으로 문제를 크게 단순화할 수 있었다.이러한 근사 방법은 종종 중심장 근사치와 함께 사용되었고 (그리고) 동일한 쉘의 전자가 동일한 방사형 부분을 갖는 조건을 부과하고, 변이 용액을 스핀 고유함수로 제한하기 위해 사용되었다.그렇더라도 하트리-를 이용해 수작업으로 솔루션을 계산하는 것.중형 원자의 Fock 방정식은 복잡했다; 작은 분자는 1950년 이전에 사용 가능했던 것보다 훨씬 더 많은 계산적 자원을 필요로 했다.

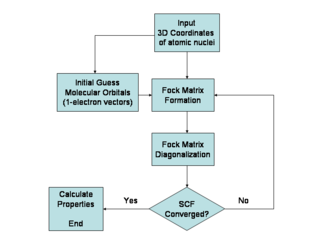
하트리-포크 알고리즘

하트리-Fock 방법은 일반적으로 Born-Oppenheimer 근사치에서 설명한 다전자 원자 또는 분자에 대한 시간 독립 슈뢰딩거 방정식을 해결하기 위해 사용된다.많은 전자 시스템에 대해 알려진 분석 솔루션이 없기 때문에(수소 원자, 이원자 수소 양이온과 같은 일렉트로닉 시스템에 대한 해결책이 있다), 문제는 수치로 해결된다.하르트리가 도입한 비선형성 때문에fock 근사치, 방정식은 반복과 같은 비선형 방법을 사용하여 해결되며, 이는 "자체 일관성 있는 필드 방법"이라는 이름을 갖게 한다.

근사치

하트리-Fock 방법은 이 작업을 처리하기 위해 다음과 같은 5가지 주요 단순화를 만든다.

• 본-오펜하이머 근사치는 본질적으로 가정된다.전분자파 함수는 사실 전자의 좌표 외에 각 핵의 좌표의 함수다.
• 전형적으로 상대론적 효과는 완전히 무시된다.모멘텀 오퍼레이터는 완전히 비-상대적이라고 가정한다.
• 변동 용액은 한정된 수의 기본 함수의 선형 조합으로 가정하며, 이 조합은 대개 직교로 선택된다(그러나 항상은 아님).유한기준 집합은 대략적으로 완전하다고 가정한다.
• 각 에너지 고유 기능은 단일 슬레이터 결정인 1전파 함수(즉, 궤도)의 비대칭 제품에서 설명할 수 있는 것으로 가정한다.
• 평균 필드 근사치는 암시되어 있다.이 가정으로부터의 일탈에서 발생하는 영향은 무시된다.이러한 영향은 종종 전자상관이라는 용어의 정의로 집합적으로 사용된다.그러나 엄격하게 사용되는 "전자상관"이라는 라벨은 쿨롱 상관관계와 페르미 상관관계를 모두 포괄하고 있으며, 후자는 전자 교환의 효과로서 하트리–에서 충분히 설명된다.포크 방식.^[9][10]이 용어에 언급된 이 방법은 쿨롱 상관관계를 소홀히 할 뿐이다.하지만, 이것은 (다른 것 중) 하트리-를 설명하는 중요한 결점이다.포크가 런던 분산을 포착하지 못하는 것.^[11]

마지막 두 개의 근사치를 완화하면 소위 하트리 이후의 많은 사람들이 생겨난다.포크 방식.

궤도상의 변동 최적화

변수 정리는 시간에 구애받지 않는 해밀턴 연산자의 경우 어떤 시험파 함수도 주어진 해밀턴어에 해당하는 진정한 지상주파 함수보다 크거나 같은 에너지 기대값을 가질 것이라고 명시하고 있다.이것 때문에 하트리-포크 에너지는 주어진 분자의 진정한 지상 에너지에 대한 상한이다.하트리-의 맥락에서-Fock 방법, 가능한 최선의 해결책은 Hartree-에 있다.Fock 한계, 즉 Hartree-의 한계기초 집합으로서의 fock 에너지는 완전성에 접근한다.(다른 하나는 Hartree–의 마지막 두 개 근사치가 있는 전체 CI 한계값이다.위에서 설명한 fock 이론은 완전히 풀렸다.두 한계를 모두 달성해야만 본-오펜하이머 근사치까지 정확한 해결책을 얻을 수 있다.)하트리-포크 에너지는 단일 슬레이터 결정요소에 대한 최소 에너지다.

하트리호의 출발점-Fock method는 스핀오르비탈이라고 알려진 대략적인 1전자파 함수의 집합이다.원자 궤도 계산의 경우, 이것들은 전형적으로 수소 같은 원자(전자가 1개뿐이지만 적절한 핵전하를 가진 원자)를 위한 궤도들이다.분자 궤도 또는 결정체 계산의 경우, 초기 근사치 1 전자파 함수는 일반적으로 원자 궤도(LCAO)의 선형 조합이다.

위의 궤도들은 평균적인 방식으로 다른 전자의 존재만을 설명할 뿐이다.인 더 하트리-Fock 방법, 다른 전자의 영향은 평균장 이론 맥락에서 설명된다.궤도는 각 슬레이터 결정요소의 에너지를 최소화하도록 요구하여 최적화된다.궤도상의 결과적인 변동조건은 새로운 일렉트로닉 운영자인 Fock 운영자로 이어진다.최소한 점령된 궤도들은 그들 사이의 단일 변형을 통해 Fock 운영자에게 비상사태를 선포한다.Fock 연산자는 효과적인 일렉트로닉 해밀턴 연산자로, 두 용어의 합이다.첫 번째는 각 전자에 대한 운동 에너지 연산자, 핵 내 반발 에너지, 핵-전자 쿨롱의 유인 조건의 합이다.두 번째는 평균장 이론 설명에서 전자 사이의 쿨롬빅 반발 조건이다. 즉, 분자 내의 다른 모든 전자를 음전하의 부드러운 분포로 처리함으로써 계산되는 시스템 내의 각 전자에 대한 순 반발 에너지다.이것이 하트리-에 내재된 주요 단순화다.Fock method이며, 상기 목록의 다섯 번째 단순화에 해당한다.

Fock 연산자는 해당 Fock 행렬을 구성하는 데 사용되는 궤도에 의존하기 때문에 Fock 연산자의 고유 기능은 차례로 새로운 궤도상에 있으며, 이는 새로운 Fock 연산자를 구성하는 데 사용될 수 있다.이런 식으로 하트리-.fock 궤도들은 총 전자 에너지의 변화가 사전 정의된 임계값 아래로 떨어질 때까지 반복적으로 최적화된다.이렇게 해서 일련의 자기 일치의 일렉트로닉 궤도(one-electron orgrounds)를 계산한다.하트리-포크 전자파 함수는 이러한 궤도상에서 생성된 슬레이터 결정요소가 된다.양자역학의 기본적 가설인 하트리-을 따른다.그런 다음 Fock Wave 함수를 사용하여 Hartree-framework 내에서 원하는 화학적 또는 물리적 특성을 계산할 수 있다.Fock 방법 및 사용된 근사치

수학적 공식화

포크 오퍼레이터

분자 해밀턴의 전자-전자 반발 용어는 서로 다른 두 전자의 좌표를 포함하기 때문에 대략적인 방법으로 재조정할 필요가 있다.이 근사치 아래(하트리-하트리 아래에 있음)Fock 알고리즘), 핵-핵 억제 조건을 제외한 정확한 해밀턴어(Hamiltonian)의 모든 용어는 닫힌 껍질 원자나 분자(각 공간 궤도 내에 두 개의 전자가 있음)에 대해 아래에 요약된 1전자 연산자의 합으로 다시 표현된다.^[12]각 연산자 기호 다음에 나오는 "(1")는 단순히 연산자가 자연적으로 1전자라는 것을 나타낸다.

${\displaystyle {\f}[\\phi _{j}\}](1)={\hat {{H}^{\text{core}(1)++\sum _{j=1}^{N/2}}[2{\j}}-{{K}}}}-{j}}}(1),}}}}}}}},}$

어디에

${\displaystyle {\hat{F}[\\\\phi _{j}\}](1)}$

궤도 $\varphi {\displaystyle {}_{}}$ ${\displaystyle j_{}}$ ${\$에 의해 생성된 일렉트로닉 Fock 연산자 입니다$.$

${\displaystyle {\hat{{H}^{\text{H}^(1)=-{\frac{1}{1}{1}:{1}nabla _{1}^{2}-\sum _{\alpha }{\frac {Z_{\alpha}}}{r_{1\alpha}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

일렉트로닉의 핵심인 해밀턴이야또한

${\displaystyle {\hat{J}_{j}(1)$

쿨롱 연산자(Coulomb operator)는 j-th 궤도 내 두 전자 각각에 기인하는 전자-전자 반발 에너지를 정의한다.^[12]마지막으로

${\displaystyle {\hat{K}_{j}(1)$

교환 연산자로, 총 N 전자파 함수의 반대칭으로 인한 전자 교환 에너지를 정의한다.^[12]이 "교환 에너지" 연산자 $K{\displaystyle \hat{}}$ ${\$은(는) 단순히 슬레이터 결정 인자의 인공물일 뿐이다$$.하트리 찾기-포크 1전파 함수는 이제 고유함수 방정식을 푸는 것과 동등하다.

${\displaystyle {\f}(1)\phi _{i}(1)=\엡실론 _{i}\phi _{i}(1),}$

여기서 $\varphi {\displaystyle {}_{}}$ ${\displaystyle i_{}}$( ${\displaystyle 1}$) ${\displaystyle \phi _{i}(1$)은$$Hartree–이라고 하는 1전파 함수의 집합이다$$.가짜 분자 궤도.

원자 궤도 선형 조합

전형적으로 현대 하트리에서는-fock 계산, 1전자파 함수는 원자 궤도의 선형 조합에 의해 근사치된다.이 원자 궤도들은 슬레이터형 궤도라고 불린다.나아가, 사용 중인 "원자 궤도"가 실제로 많은 양의 계산 시간을 절약하기 위해 슬레이터형 궤도보다 하나 이상의 가우스형 궤도선의 선형 결합으로 구성되는 것은 매우 흔한 일이다.

다양한 기본 세트가 실무에 사용되며, 대부분은 가우스 함수로 구성된다.일부 애플리케이션에서는 Gram-Schmidt 프로세스와 같은 직교화 방법을 수행하여 일련의 직교 기준 함수를 생성한다.이것은 원칙적으로 컴퓨터가 중첩 행렬을 ID 행렬로 효과적으로 변환하여 Roothan-Hall 방정식을 풀 때 계산 시간을 절약할 수 있다.하지만 분자 하트리-를 위한 대부분의 현대 컴퓨터 프로그램에서는Fock 계산은 직교화의 높은 수치 비용과 일반화된 고유값 문제를 해결하기 위한 보다 효율적이고 종종 희박한 알고리즘의 출현으로 인해 이 절차를 따르지 않으며, 이 중 Rootha-Hall 방정식이 예시된다.

수치안정성

수치적 안정성은 이 절차에서 문제가 될 수 있으며 이러한 불안정성을 극복하는 다양한 방법이 있다.가장 기본적이고 일반적으로 적용할 수 있는 것 중 하나는 F-믹스 또는 댐핑이라고 불린다.F-믹스(F-mixing)를 사용하면 단전파 함수가 계산되면 직접 사용하지 않는다.대신에, 그 계산된 파동함수와 그 전자에 대한 이전의 파동함수의 일부 조합이 사용되며, 가장 일반적인 조합은 계산된 파동함수와 바로 앞의 파동함수의 단순한 선형 결합이다.원자 계산을 위해 하르트리가 고용한 교묘한 회피는 핵 전하를 증가시켜 모든 전자를 더욱 가깝게 끌어당기는 것이었다.시스템이 안정화됨에 따라, 이것은 점차적으로 올바른 충전으로 줄어들었다.분자 계산에서 유사한 접근법이 양이온에 대한 파동 함수를 먼저 계산한 다음 이러한 궤도들을 중성 분자의 시작점으로 사용하는 경우도 있다.현대 분자 하트리-Fock 컴퓨터 프로그램은 다양한 방법을 사용하여 Roothan-Hall 방정식의 정합성을 보장한다.

약점, 확장 및 대안

"하트리–" 절에 요약된 다섯 가지 단순화 중Fock 알고리즘", 5번째가 일반적으로 가장 중요하다.전자 상관 관계를 소홀히 하면 실험 결과에서 큰 편차를 초래할 수 있다.이러한 약점에 대한 여러 가지 접근법(Post-Hartree–후하트리)이라고 통칭함fock 방법은 다전파 함수에 전자 상관관계를 포함하도록 고안되었다.이러한 접근방식 중 하나인 뫼르-플레셋 섭동 이론은 상관관계를 포크 연산자의 섭동으로 취급한다.다른 것들은 다중 구성 자기 일치 필드, 구성 상호작용, 2차 구성 상호작용 및 완전한 활성 공간 SCF(CASCF)와 같은 슬레이터 결정요인의 선형 조합 측면에서 진정한 다중 전자파 함수를 확장한다.다른 것들(변동 양자 몬테 카를로 등)은 하트리-을 수정한다.포크파 함수를 상관 함수("Jastrow" 인자)로 곱하여 포크파 함수("Jastrow" 인자)는 독립된 단일 입자 함수로 분해될 수 없는 다중 전자의 함수인 용어다.

하트리 대안으로-일부 경우에 사용되는 fock 계산은 밀도 기능 이론으로, 대략적이긴 하지만 교환 에너지와 상관 관계 에너지를 모두 취급한다.실제로, 두 가지 방법의 혼합물인 계산을 사용하는 것이 일반적이다. 즉, 인기 있는 B3LYP 체계는 그러한 복합적인 기능적 방법 중 하나이다.또 다른 선택은 현대적인 발란스 본드 방법을 사용하는 것이다.

소프트웨어 패키지

Hartree를 처리하는 것으로 알려진 소프트웨어 패키지 목록Fock 계산, 특히 분자와 고형분에 대한 계산은 양자 화학 및 고체 상태 물리학 소프트웨어의 목록을 참조한다.

참고 항목

참조

원천

• Levine, Ira N. (1991). Quantum Chemistry (4th ed.). Englewood Cliffs, New Jersey: Prentice Hall. pp. 455–544. ISBN 0-205-12770-3.
• Cramer, Christopher J. (2002). Essentials of Computational Chemistry. Chichester: John Wiley & Sons, Ltd. pp. 153–189. ISBN 0-471-48552-7.
• Szabo, A.; Ostlund, N. S. (1996). Modern Quantum Chemistry. Mineola, New York: Dover Publishing. ISBN 0-486-69186-1.

외부 링크

• 비 쿨롱 중앙장을 가진 원자의 파동 역학 제2부. 1928년 1월, Cambridge 철학회의 수학과정 D. R. Hartree의 일부 결과와 토론
• C에 의한 하트리-폭크 분자 궤도이론 소개데이비드 셰릴 (2000년 6월)
• 평균필드 이론: E. 파바리니, E. 코흐, J. 밴 덴 브링크, G. 사와츠키: 양자 물질: 실험과 이론, 쥴리히 2016, ISBN 978-3-95806-159-0