분자 궤도 이론

Molecular orbital theory
참고 항목: 분자 궤도
전자 구조 방법
발란스 본드 이론
콜슨-피셔 이론
일반화 발란스 본드
모던발란스 본드
분자 궤도 이론
하트리-포크 방식
반감기 양자화학법
뫼르-플레셋 섭동 이론
구성 상호 작용
커플링 클러스터
다중 구성 자체 일관성 필드
양자화학복합법
퀀텀 몬테 카를로
밀도함수이론
시간 의존적 밀도 기능 이론
토마스-페르미 모델
궤도무밀도기능이론
전자 밴드 구조
거의 자유 전자 모델
타이트 바인딩
머핀틴 근사치
k·p 섭동설
빈 격자 근사치

화학에서 분자 궤도 이론(MOT 이론 또는 MOT 이론)은 양자 역학을 이용하여 분자의 전자 구조를 기술하는 방법이다. 그것은 20세기 초에 제안되었다.

분자 궤도 이론에서 분자 속의 전자는 원자 사이의 개별 화학 결합에 할당되지 않고 분자 전체의 원자핵의 영향 아래에서 움직이는 것으로 취급된다.[1] 양자역학은 전자의 공간적, 에너지적 특성을 분자 내 둘 이상의 원자를 둘러싸고 원자 사이에 발란스 전자를 포함하는 분자 궤도라고 설명한다.

분자 궤도 이론은 원자 궤도(LCAO)의 선형 결합으로서 결합 전자 상태(분자 궤도)를 근사하게 함으로써 화학 결합 연구에 혁명을 일으켰다. 이러한 근사치는 밀도 기능 이론(DFT) 또는 하트리–을 적용하여 만들어진다.슈뢰딩거 방정식에 대한 Fock(HF) 모델.

분자 궤도 이론과 발란스 결합 이론은 양자 화학의 기초 이론이다.

LCAO(원자 궤도) 방법의 선형 결합

LCAO 방법에서 각 분자는 일련의 분자 궤도를 가지고 있다. 분자궤도파 함수j ψ은 다음 방정식에 따라 n 성분 원자궤도i weighted의 단순 가중 합으로 작성할 수 있다고 가정한다.[2]

이 방정식을 슈뢰딩거 방정식으로 대체하고 변동원리를 적용하여 cij 계수를 숫자로 결정할 수 있다. 변동원리는 양자역학에서 각 원자 궤도 기초의 계수를 쌓기 위해 사용되는 수학 기법이다. 계수가 크면 궤도 기초가 특정 기여 원자 궤도(hence)로 더 많이 구성됨을 의미한다. 분자 궤도(holecular optives)는 그러한 유형으로 가장 잘 특징지어진다. 궤도 기여를 원자 궤도의 선형 조합으로 정량화하는 이 방법은 계산 화학에서 사용된다. 시스템에 추가적인 단일 변환을 적용하여 일부 계산 체계에서 수렴을 가속화할 수 있다. 분자 궤도 이론은 1930년대에 발란스 본드 이론의 경쟁자로 여겨졌는데, 그 두 방법이 밀접하게 연관되어 있고 확장되었을 때 그것들이 등가물이 된다는 것이 실현되기 전이었다.

원자 궤도 조합이 대략적인 분자 궤도 조합으로 적합하려면 크게 세 가지 요건이 있다.

  1. 원자 궤도 조합은 정확한 대칭을 가져야 하며, 이는 분자 대칭 그룹의 정확한 불가역적 표현에 속해야 함을 의미한다. 대칭 적응 선형 결합, 즉 SALC를 사용하면 정확한 대칭의 분자 궤도를 형성할 수 있다.
  2. 원자 궤도 또한 우주 내에서 겹치도록 해야 한다. 그들은 서로 너무 멀리 떨어져 있으면 결합하여 분자 궤도를 형성할 수 없다.
  3. 원자 궤도는 분자 궤도로 결합하기 위해 유사한 에너지 수준에 있어야 한다.

역사

분자 궤도 이론은 발란스 본드 이론이 확립된 후(1927년) 주로 프리드리히 헌트, 로버트 멀리켄, 존 C의 노력으로 개발되었다. 슬레이터, 그리고 존 레너드 존스.[3] MO 이론은 원래 훈드-물리켄 이론이라고 불렸다.[4] 물리학자 겸 물리 화학자인 에리히 후켈에 따르면 분자 궤도 이론의 첫 양적 사용은 1929년 레나드 존스의 논문이었다.[5][6] 본 논문은 1931년 독자적인 설명을 내놓았던 발란스 본드 이론 이전에 파라마그니즘[7](분자 궤도도 § 디옥시겐 참조)[8]을 설명한 다이옥시겐 분자의 3중 접지 상태를 예측했다. 궤도라는 단어는 1932년에 멀리켄에 의해 소개되었다.[4] 1933년까지 분자 궤도 이론은 유효하고 유용한 이론으로 받아들여졌다.[9]

에리히 후켈은 1931년부터 파이 전자의 MO 에너지 결정을 위한 후켈 분자 궤도(HMO) 방법으로 불포화 탄화수소 분자에 분자 궤도 이론을 적용했고, 이를 결합 및 방향족 탄화수소에 적용했다.[10][11] 이 방법은 벤젠과 같은 6개의 파이 전자를 가진 분자의 안정성에 대한 설명을 제공했다.

분자 궤도 파동 기능의 첫 번째 정확한 계산은 1938년 찰스 쿨슨이 수소 분자에 대해 만든 것이었다.[12] 1950년까지 분자 궤도 이론은 완전히 자기 일치 분야인 해밀턴의 고유 기능(파장 함수)으로 정의되었고, 이때 분자 궤도 이론은 완전히 엄격하고 일관성이 있게 되었다.[13] 이 엄격한 접근법은 하트리-로 알려져 있다.분자에 대한 fock 방법은 원자에 대한 계산에서 기원이 있었지만. 분자에 대한 계산에서 분자 궤도는 원자 궤도 기준 설정의 관점에서 확장되어 로타 방정식으로 이어진다.[14] 이것은 많은 아비니시오 양자 화학 방법의 개발로 이어졌다. 이와 병행하여 분자 궤도이론은 현재 반감기 양자화학법으로 알려진 방법에서 경험적으로 파생된 일부 매개변수를 사용하여 보다 근사하게 적용되었다.[14]

분자 궤도이론의 성공은 또한 1930년대와 1940년대에 수정장 이론의 대안으로 개발된 리간드장 이론을 낳았다.

궤도 유형

두 H 원자의 원자 궤도로부터 H2(센트레)의 분자 궤도 형성을 보여주는 MO 도표. 저에너지 MO는 두 H 핵 사이에 집중된 전자 밀도와 결합하고 있다. 고에너지 MO는 각 H핵 뒤에 전자 밀도가 집중된 안티 본딩이다.

분자 궤도(MO) 이론은 원자 궤도(LCAO)의 선형 결합을 사용하여 원자 사이의 결합에서 비롯되는 분자 궤도를 나타낸다. 이들은 흔히 본딩, 항균, 비본딩의 세 가지 유형으로 나뉜다. 공전궤도를 결합하면 주어진 원자 쌍 사이의 영역에 전자 밀도가 집중되므로, 그것의 전자 밀도는 두 개의 핵 각각을 다른 원자 쪽으로 끌어당겨 두 원자를 함께 고정시키는 경향이 있을 것이다.[15] 반본딩 궤도(anti-bonding orbound)는 각각의 핵(즉, 다른 원자로부터 가장 멀리 있는 각 원자의 측면)에 전자 밀도를 "뒤로" 집중시키고, 따라서 두 핵 각각을 다른 핵으로부터 떼어내어 실제로 두 핵 사이의 결합을 약화시키는 경향이 있다. 비결합 궤도에 있는 전자는 서로 긍정적이거나 부정적으로 상호작용하지 않는 원자 궤도와 연관되는 경향이 있으며, 이러한 궤도에 있는 전자는 결합 강도에 기여하거나 이탈하지 않는다.[15]

분자 궤도는 그들이 형성되는 원자 궤도의 종류에 따라 더욱 나누어져 있다. 화학 물질은 서로 상호작용할 때 그들의 궤도가 에너지가 낮아지면 결합 상호작용을 형성할 것이다. 전자 구성(전자 구름 모양)과 에너지 수준에 따라 다른 결합 궤도를 구별한다.

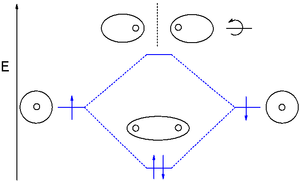
분자의 분자 궤도는 분자 궤도 도표에서 설명할 수 있다.

공통 본딩 궤도는 본드 축에 대칭인 시그마(시그마) 궤도, 본드 축을 따라 결절면이 있는 파이(PI) 궤도다. 결합 축을 따라 각각 2면과 3면의 결절면이 있는 델타(Δ) 궤도 및 피(phi) 궤도는 덜 흔하다. 궤도 반대는 별표를 추가하여 나타낸다. 예를 들어, 항균 파이 궤도(Antiboning pi arbit)는 π*로 표시될 수 있다.

개요

MOT는 화학적 결합에 대한 전지구적이고 분산된 관점을 제공한다. MO 이론에서, 양자 조건은 전자가 특정 양자 법칙에 의해 허용되는 고유체 내에 있는 한 임의의 많은 수의 핵의 영향 아래 이동하도록 허용하기 때문에 분자 내의 어떤 전자도 분자의 어느 곳에서도 발견될 수 있다. 따라서 고주파 빛이나 다른 수단을 통해 필요한 양의 에너지로 흥분하면 전자는 고에너지 분자 궤도로 전환될 수 있다. 예를 들어, 수소 이원자 분자의 단순한 경우, 단일 전자가 결합 궤도로부터 항균 궤도까지 촉진되는 것은 UV 방사선 하에서 발생할 수 있다. 이러한 승진은 두 수소 원자의 결합을 약화시키고 광분해(빛의 흡수에 의한 화학적 결합의 깨짐)로 이어질 수 있다.

분자 궤도이론은 자외선 가시 분광법(UV-VIS)을 해석하는 데 사용된다. 분자의 전자 구조에 대한 변화는 특정 파장에서 빛의 흡수로 볼 수 있다. 더 낮은 에너지의 한 궤도상에서 더 높은 에너지 궤도로의 전자의 이동에 의해 지시되는 이러한 신호에 할당될 수 있다. 최종 상태에 대한 분자 궤도 도표는 흥분 상태에 있는 분자의 전자적 성질을 설명한다.

비록 MO 이론에서 일부 분자 궤도는 특정 쌍의 분자 원자들 사이에서 더 국부적인 전자를 보유할 수 있지만, 다른 궤도들은 분자 위에 더 균일하게 퍼져 있는 전자를 보유할 수도 있다. 따라서 전체적으로 본딩은 MO이론에서 훨씬 더 비초점화되어 발란스 본드(VB) 이론보다 동등한 비정수 본드 순서를 가진 공명 분자에 더 적용 가능하다. 이것은 MO 이론을 확장된 시스템의 설명에 더 유용하게 만든다.

로버트 S. 분자 궤도 이론의 출현에 적극적으로 참여한 멀리켄은 각 분자를 자급자족 단위로 간주한다. 그는 자신의 글에서 다음과 같이 주장한다.

...분자를 특정 원자 또는 이온 단위로 간주하려는 시도들은 특수한 경우 근사치 또는 계산 방법으로서가 아닌 이상 다소 무의미하다고 간주된다[…]. 분자는 여기서 핵의 집합으로 간주되며, 각 핵은 외부 장에서 자유 원자의 그것과 매우 유사한 전자 구성으로 그룹화된다. 단, 각 핵들을 둘러싼 전자 구성의 외부는 부분적으로, 두 개 이상의 핵에 공동으로 속한다는 것을 제외한다.[16]

그 예로 6개의 탄소 원자와 3개의 이중 결합으로 이루어진 방향성 육각형 고리인 벤젠 CH의
6
6 MO 설명이 있다. 이 분자에서는 30개의 총 발란스 본딩 전자 중 24개(탄소 원자에서 24개, 수소 원자에서 6개)가 12㎛(시그마) 본딩 궤도에 위치하는데, 이 원자는 발란스 본딩 설명서의 전자와 유사하게 원자 쌍(C-C 또는 C-H) 사이에 대부분 위치한다. 그러나 벤젠에서는 나머지 6개의 본딩 전자가 링 주위로 소산되는 3㎛(pi) 분자 본딩 궤도에 위치한다. 이 전자들 중 두 개는 6개 원자의 궤도 기여도가 동일한 MO 안에 있다. 나머지 4개의 전자는 서로 직각으로 수직 노드가 있는 궤도상에 있다. VB 이론에서와 같이, 이 여섯 개의 델로컬화된 π 전자는 모두 링 평면 위와 아래에 존재하는 더 큰 공간에 존재한다. 벤젠의 모든 탄소-탄소 결합은 화학적으로 동등하다. MO 이론에서 이것은 3개의 분자 π 궤도들이 결합하여 6개의 탄소 원자에 6개의 여분의 전자를 균등하게 퍼뜨린다는 사실의 직접적인 결과물이다.

벤젠의 구조

메탄, CH와
4 같은 분자에서는 8개의 발란스 전자가 5개의 원자 전체에 퍼져 있는 4개의 MO에서 발견된다. MO를 국부적인 4개의 sp궤도로3 변환하는 것이 가능하다. 리너스 폴링은 1931년 탄소 2s와 2p 궤도를 혼합하여 수소 1s 기본 함수를 직접 가리키고 최대 중복성을 특징으로 했다. 단, 이온화 에너지와 스펙트럼 흡수 밴드의 위치를 예측하는 데는 탈색 MO 설명이 더 적절하다. 메탄이 이온화되면 발란스 MO에서 하나의 전자가 추출되는데, 이는 s 본딩이나 삼각 분해 p 본딩 수준에서 나올 수 있으며, 두 개의 이온화 에너지를 산출한다. 이에 비해 VB 이론에서의 설명은 더욱 복잡하다. sp3 궤도상에서 전자 1개가 제거되면 공명은 4개의 발란스 본드 구조 사이에서 발생하는데, 각각 1개의 전자 본드와 3개의 2개의 전자 본드가 있다. 삼엽 퇴화 T와2 A1 이온화 상태(CH4+)는 이 네 가지 구조의 서로 다른 선형 조합에서 생성된다. 이온화 상태와 지면 상태의 에너지 차이는 두 이온화 에너지를 준다.

벤젠에서와 마찬가지로 베타 카로틴, 엽록소, 헤메와 같은 물질에서는 orbit 궤도상의 일부 전자가 분자 내 먼 거리에 걸쳐 분자 궤도에 퍼져 있어 낮은 에너지(가시 스펙트럼)에서 빛을 흡수하게 되어 이러한 물질의 특징적인 색상이 설명된다.[17] 분자에 대한 이 및 기타 분광학적 데이터는 궤도 대칭 일치 원리로 전제된 궤도의 혼합을 포함하여 다중 입자 궤도와 관련된 전자 상태를 강조하면서 MO 이론에서 잘 설명된다.[15] 또한 같은 MO 원리는 흑연에 존재하는 육각형 원자판의 평면 방향에서 높은 전기 전도도와 같은 일부 전기 현상을 자연적으로 설명한다. 이는 절반만 채워진 p 궤도들의 연속적인 대역 중첩에서 기인하며 전기 전도를 설명한다. MO이론은 흑연 원자판의 일부 전자가 임의의 거리에 걸쳐 완전히 소산되고, 흑연 시트 전체를 덮고 있는 매우 큰 분자 궤도에 존재한다는 것을 인식하고, 따라서 어떤 전자는 금속 속에 거주한 것처럼 자유롭게 움직이고 따라서 시트 평면에서 전기를 전도한다.

참고 항목

참조

  1. ^ Daintith, J. (2004). Oxford Dictionary of Chemistry. New York: Oxford University Press. ISBN 978-0-19-860918-6.
  2. ^ Licker, Mark, J. (2004). McGraw-Hill Concise Encyclopedia of Chemistry. New York: McGraw-Hill. ISBN 978-0-07-143953-4.{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크)
  3. ^ Coulson, Charles, A. (1952). Valence. Oxford at the Clarendon Press.
  4. ^ a b Mulliken, Robert S. (1972) [1966]. "Spectroscopy, Molecular Orbitals, and Chemical Bonding" (PDF) (Press release). Nobel Lectures, Chemistry 1963–1970. Amsterdam: Elsevier Publishing Company.
  5. ^ Hückel, Erich (1934). "Theory of free radicals of organic chemistry". Trans. Faraday Soc. 30: 40–52. doi:10.1039/TF9343000040.
  6. ^ Lennard-Jones, J.E. (1929). "The electronic structure of some diatomic molecules". Trans. Faraday Soc. 25: 668–686. Bibcode:1929FaTr...25..668L. doi:10.1039/TF9292500668.
  7. ^ 콜슨, C.A. 발랑스 (제2편, 옥스퍼드 대학 출판부 1961), 페이지 103
  8. ^ Pauling, Linus (1931). "The Nature of the Chemical Bond. II. The One-Electron Bond and the Three-Electron Bond". J. Am. Chem. Soc. 53 (9): 3225–3237. doi:10.1021/ja01360a004.
  9. ^ Hall, George G. (1991). "The Lennard-Jones paper of 1929 and the foundations of Molecular Orbital Theory". Advances in Quantum Chemistry. 22: 1–6. Bibcode:1991AdQC...22....1H. doi:10.1016/S0065-3276(08)60361-5. ISBN 978-0-12-034822-0. ISSN 0065-3276.
  10. ^ E. Hukel, Zeitschrift für Phyk, 70, 204 (1931); 72, 310 (1931); 76, 628 (1932); 83, 632 (1933).
  11. ^ 유기화학자들을 위한 휴켈 이론, C. A. 콜슨, B. O'Leary and R. B. Mallion, Academic Press, 1978.
  12. ^ Coulson, C.A. (1938), "Self-consistent field for molecular hydrogen", Mathematical Proceedings of the Cambridge Philosophical Society, 34 (2): 204–212, Bibcode:1938PCPS...34..204C, doi:10.1017/S0305004100020089
  13. ^ Hall, G.G. (7 August 1950). "The Molecular Orbital Theory of Chemical Valency. VI. Properties of Equivalent Orbitals". Proc. Roy. Soc. A. 202 (1070): 336–344. Bibcode:1950RSPSA.202..336H. doi:10.1098/rspa.1950.0104. S2CID 123260646.
  14. ^ a b Jensen, Frank (1999). Introduction to Computational Chemistry. John Wiley and Sons. ISBN 978-0-471-98425-2.
  15. ^ a b c Miessler와 Tarr (2013), 무기화학, 5부 117-165, 475-534.
  16. ^ Mulliken, R. S. (October 1955). "Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I". The Journal of Chemical Physics. 23 (10): 1833–1840. doi:10.1063/1.1740588. ISSN 0021-9606.
  17. ^ 그리피스, J.S., L.E. 오르골. "리간드 필드 이론" Q. 화학신부. Soc. 1957, 11, 381-383

외부 링크