유전자 조절망

Gene regulatory network
유전자 조절 네트워크의 구조
유전자 조절 네트워크의 제어 과정

유전자(또는 유전자) 조절 네트워크(GRN)는 mRNA와 단백질의 유전자 발현 수준을 제어하기 위해 세포 내의 다른 물질과 상호 작용하는 분자 조절 장치의 집합이다.GRN은 또한 형태 형성, 즉 신체 구조의 생성에서 중심적인 역할을 하며, 이는 다시 진화 발달 생물학(evo-devo)의 중심이다.

조절기는 DNA, RNA, 단백질 및 이들의 복합체일 수 있습니다.상호작용은 (전사된 RNA 또는 번역된 단백질을 통해) 직접 또는 간접적일 수 있습니다.일반적으로 각 mRNA 분자는 특정 단백질(또는 단백질 세트)을 만들기 위해 계속된다.경우에 따라 이 단백질은 구조적이며 세포막 또는 세포 내에 축적되어 특정 구조적 특성을 부여합니다.다른 경우 단백질은 효소, 즉 식품원이나 독소의 분해와 같은 특정 반응을 촉매하는 마이크로 기계일 것이다.일부 단백질은 다른 유전자를 활성화시키는 역할만 하는데, 이것들은 조절 네트워크나 계단식 조절의 주요 주체인 전사 인자들이다.다른 유전자가 시작될 때 프로모터 영역에 결합함으로써 다른 단백질의 생산을 시작하는 등 유전자가 활성화됩니다.일부 전사 인자는 [1]억제적입니다.

단세포 생물에서 조절 네트워크는 외부 환경에 반응하여 이 환경에서 생존하기 위해 주어진 시간에 세포를 최적화합니다.따라서 효모세포는 설탕 용액에서 발견되는 유전자를 활성화하여 [2]당을 알코올로 가공하는 효소를 만들 것입니다.우리가 와인 제조와 관련된 이 과정은 효모세포가 어떻게 살아가고, 증식할 에너지를 얻는가에 대한 것입니다. 이것은 정상적인 상황에서 생존 가능성을 높일 것입니다.

다세포 동물에서도 같은 원리가 체형을 [3]조절하는 유전자 연쇄 작용에 적용되어 왔다.세포가 분열할 때마다, 두 개의 세포는 같은 게놈을 완전히 포함하고 있지만, 어떤 유전자가 활성화되고 단백질을 만드는지에 따라 달라질 수 있다.때때로 '자급 피드백 루프'는 셀이 자신의 정체성을 유지하고 그것을 전달하도록 보장합니다.염색질 변형이 전사를 차단하거나 허용함으로써 세포기억을 제공할 수 있는 후생유전학의 메커니즘은 잘 알려져 있지 않다.다세포 동물의 주요 특징은 형태소 구배를 사용하는 것인데, 이것은 사실상 세포에게 그것이 몸 안의 어디에 있고, 따라서 어떤 종류의 세포가 되어야 하는지를 알려주는 위치 결정 시스템을 제공한다.하나의 세포에서 반응하는 유전자는 세포에서 나와 인접한 세포를 통해 확산되는 생성물을 만들 수 있으며, 특정 역치 이상일 때만 세포에 들어가 유전자가 반응한다.따라서 이 세포들은 새로운 운명으로 유도되고, 심지어 원래의 세포에 신호를 보내는 다른 형태소를 생성할 수도 있다.장거리에서는 모르포겐이 신호 전달의 활성 프로세스를 사용할 수 있습니다.이러한 신호 전달은 배아 발생, 즉 일련의 순차적 단계를 통해 처음부터 신체 계획의 구축을 제어합니다.그들은 또한 피드백 과정을 통해 성인의 몸을 통제하고 유지하며, 돌연변이로 인한 그러한 피드백의 상실은 암에서 보이는 세포 증식의 원인이 될 수 있다.구조를 만드는 이 과정과 병행하여, 유전자 캐스케이드는 각 세포에 필요한 물리적 특성을 부여하는 구조 단백질을 만드는 유전자를 작동시킨다.

개요

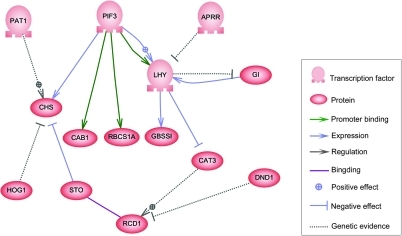
한 차원에서는, 생물학적 세포는 생물학적 화학물질의 "부분적으로 혼합된 가방"으로 생각될 수 있다 – 유전자 조절 네트워크의 논의에서, 이러한 화학물질은 대부분 유전자 발현에서 발생하는 메신저 RNA와 단백질이다.이러한 mRNA와 단백질은 다양한 수준의 특이성을 가지고 서로 상호작용합니다.일부는 세포 주위에 확산된다.다른 것들은 세포막에 결합되어 환경의 분자와 상호작용합니다.다른 것들은 세포막을 통과하여 다세포 유기체의 다른 세포에 대한 장거리 신호를 매개한다.이러한 분자와 그 상호작용은 유전자 조절 네트워크를 구성한다.전형적인 유전자 조절 네트워크는 다음과 같습니다.

규제 네트워크의 예

이 네트워크의 노드는 유전자, 단백질, mRNA, 단백질/단백질 복합체 또는 세포 과정을 나타낼 수 있습니다.수직선을 따라 놓여 있는 것으로 묘사되는 노드는 셀/환경 인터페이스와 관련지어지며, 다른 노드는 자유 부동이며 확산될 수 있습니다.노드 사이의 가장자리는 DNA, mRNA, miRNA, 단백질 또는 분자 과정 사이의 개별 분자 반응에 해당할 수 있는 노드 간의 상호작용을 나타내지만, 실험적으로 얻은 정보의 부족은 종종 suc에 따라 일부 반응이 모델링되지 않음을 암시한다.h 상세 수준.이러한 상호작용은 유도성(일반적으로 화살표 또는 + 기호로 표시됨)일 수 있으며, 한 개의 집중도가 증가하면 다른 하나의 억제성(채운 원, 뭉툭한 화살표 또는 마이너스 기호로 표시됨)이 증가하고, 한 개의 증가가 다른 하나의 감소로 이어지며, 상황에 따라 다른 하나의 또는 이중으로 이어질 수 있습니다.es 레귤레이터는 타깃노드를 활성화 또는 억제할 수 있습니다.노드는 직접 또는 간접적으로 스스로를 조절할 수 있으며, 토폴로지 네트워크에서 종속성의 주기적 체인을 형성하는 피드백 루프를 생성할 수 있습니다.네트워크 구조는 한 물질이 연결된 다른 모든 물질에 영향을 미치는 다양한 방법을 설명하는 시스템의 분자 또는 화학 역학의 추상화입니다.실제로 이러한 GRN은 특정 시스템의 생물학적 문헌에서 추론되며 일련의 관련된 생화학 반응에 대한 집합적 지식의 증류를 나타낸다.GRN의 수동 큐레이션을 가속화하기 위해 최근 일부 노력은 텍스트 마이닝, 큐레이티드 데이터베이스, 대규모 데이터로부터의 네트워크 추론, 모델 체크 및 기타 정보 추출 기술을 이러한 [4]목적으로 사용하려고 시도하고 있습니다.

유전자는 네트워크의 노드로서 볼 수 있으며 입력은 전사인자 등의 단백질이며 출력은 유전자 발현 수준이다.노드의 값은 이전 시간 스텝의 레귤레이터 값에 따라 달라지는 함수에 따라 달라집니다(부울 네트워크에서는 부울 함수(일반적으로 AND, OR 및 NOT)입니다).이러한 기능은 세포 내에서 세포 행동을 결정하는 일종의 정보 처리를 수행하는 것으로 해석되어 왔다.세포 내의 기본 동인은 "세포 기억"의 일종으로서 세포의 공간적 좌표(세포 또는 조직 내 위치)와 시간적 좌표(세포 주기 또는 발달 단계)를 모두 결정하는 일부 단백질의 농도이다.유전자 네트워크는 이제 겨우 이해되기 시작했고, 생물학은 유전자에서 신호 경로, 세포 또는 조직 [5]수준까지 증가하는 복잡성 수준에서 시스템의 행동을 이해하는 것을 돕기 위해 각 유전자 "노드"의 기능을 추론하는 것을 시도하는 다음 단계이다.

GRN의 수학적 모델은 모델링되는 시스템의 동작을 포착하기 위해 개발되었으며, 어떤 경우에는 실험적인 관찰에 대응하는 예측을 생성한다.다른 경우에, 모델은 실험적으로 시험할 수 있는 정확한 새로운 예측을 하는 것으로 증명되었고, 따라서 실험실의 프로토콜 설계에서 때때로 고려되지 않는 실험에서 탐구할 수 있는 새로운 접근법을 제안합니다.모델링 기술에는 미분 방정식(ODE), 부울 네트워크, 페트리 네트, 베이지안 네트워크, 그래픽 가우스 네트워크 모델, 확률적 및 프로세스 계산 [6]등이 있습니다.반대로 시계열 관측치 집합을 가장 잘 설명하는 GRN의 모델을 생성하기 위한 기법이 제안되었다.최근 히스톤 수식의 ChIP-seq 신호는 RNA [7]수준과 비교하여 프로모터의 전사 인자 모티브와 더 관련이 있는 것으로 나타났다.따라서 시계열 히스톤 수정 ChIP-seq는 발현 수준에 기초한 방법과 비교하여 유전자 조절 네트워크의 보다 신뢰할 수 있는 추론을 제공할 수 있다.

구조와 진화

글로벌 기능

유전자 규제 네트워크는 일반적으로 계층적 규제 체제 내에 내포된 소수의 고도로 연결된 노드(허브)와 제대로 연결되지 않은 많은 노드로 구성된다.따라서 유전자 조절 네트워크는 계층적 규모의 자유 네트워크 [8]토폴로지에 가깝다.이것은 대부분의 유전자가 제한된 다방성을 가지고 있고 조절 [9]모듈 내에서 작동한다는 관점과 일치한다.이 구조는 중복된 유전자가 보다 고도로 연결된 [8]유전자에 우선적으로 부착되기 때문에 진화하는 것으로 생각된다.최근의 연구에서도 자연선택은 [10]접속성이 희박한 네트워크를 선호하는 경향이 있는 것으로 나타났습니다.

네트워크가 진화하려면 주로 두 가지 방법이 있는데, 두 가지 방법이 동시에 발생할 수 있습니다.첫 번째는 노드(genes)의 덧셈 또는 뺄셈에 의해 네트워크토폴로지가 변경되거나 네트워크의 일부(모듈)가 다른 컨텍스트로 표현될 수 있다는 것입니다.Drosophila Hippo 시그널링 경로는 좋은 예를 제공합니다.하마의 신호 경로는 유사분열 성장과 유사분열 후 세포 [11]분화를 모두 통제한다.최근 Hippo 시그널링 경로가 작동하는 네트워크는 이 두 기능 간에 다르며, 이는 다시 Hippo 시그널링 경로의 동작을 변화시키는 것으로 밝혀졌다.이는 [11]Hippo 신호 경로가 상황에 따라 여러 기능에 사용할 수 있는 보존된 조절 모듈로 작동함을 나타냅니다.따라서 네트워크토폴로지를 변경하면 보존된 모듈이 여러 기능을 수행하고 네트워크의 최종 출력을 변경할 수 있습니다.네트워크가 진화할 수 있는 두 번째 방법은 문자 변환 계수가 cis-regulation 요소에 얼마나 강하게 결합할 수 있는지 등 노드 간의 상호작용 강도를 변경하는 것입니다.이러한 네트워크 가장자리 강도의 변화는 외음 세포 운명 패턴의 외음 세포 변화 사이의 [12]기초가 되는 것으로 나타났다.

로컬 기능

피드 포워드 루프

유전자 조절 네트워크의 또 다른 특징은 네트워크 모티브로 알려진 특정 반복 하위 네트워크의 풍부함이다.네트워크 모티브는 큰 네트워크를 작은 블록으로 분할할 때 반복적인 토폴로지 패턴으로 간주할 수 있습니다.이전 분석은 무작위로 생성된 [13][14][15]네트워크보다 유전자 조절 네트워크에서 더 자주 나타나는 여러 유형의 모티브를 발견했다.예를 들어, 이러한 모티브 중 하나는 피드 포워드 루프라고 불리며, 3개의 노드로 구성됩니다.이 모티브는 파리, 선충, [15]인간의 유전자 조절 네트워크에서 알 수 있듯이 세 개의 노드로 구성된 가능한 모티브 중 가장 풍부하다.

농축된 모티브는 수렴 진화를 따르도록 제안되어 특정 규제 [16]목적을 위한 "최적의 설계"임을 시사한다.예를 들어, 모델링을 통해 피드포워드 루프는 노드 A의 변화(집중 및 액티비티 측면에서)와 노드 C의 표현 역학을 조정할 수 있으며, 서로 다른 입출력 [17][18]동작을 생성할 수 있음을 알 수 있습니다.대장균의 갈락토스 이용 시스템은 갈락토스 이용 오퍼론 galETK의 활성화를 촉진하는 피드포워드 루프를 포함하고 있어 포도당이 [19]고갈되었을 때 갈락토스로의 대사 전환을 잠재적으로 촉진한다.E.coli의 아라비노오스 이용 시스템의 피드포워드 루프는 아라비노오스 이화 작용 오퍼론 및 운반체의 활성화를 지연시켜 상류 신호 [20]경로의 일시적인 변동으로 인한 불필요한 대사 전이를 잠재적으로 피한다.마찬가지로 Xenopus의 Wnt 신호 경로에서 피드-포워드 루프는 β-카테닌 수준의 절대 변화가 아닌 접힘 변화에 반응하여 잠재적으로 [21]β-카테닌 수준의 변동에 대한 저항을 증가시키는 접힘 변화 검출기 역할을 한다.수렴 진화 가설에 따라 피드포워드 루프의 강화는 빠른 응답과 소음 내성을 위한 적응이 될 것이다.최근 연구에 따르면 일정한 포도당의 환경에서 자란 효모는 포도당 신호 경로와 성장 조절 경로에서 돌연변이를 일으켜 환경 변화에 반응하는 조절 성분이 일정한 [22]환경 하에서는 불필요하다는 것을 알 수 있다.

한편, 일부 연구자들은 네트워크 모티브의 풍부화가 [23]비적응적이라고 가정한다.즉, 유전자 조절 네트워크는 제안된 입출력 행동에 대한 특정 선택 없이 유사한 구조로 진화할 수 있다.이 가설에 대한 지지는 종종 컴퓨터 시뮬레이션에서 나온다.예를 들어, 무작위로 노드를 다시 배선함으로써 유전자 조절 네트워크의 진화를 시뮬레이션하는 모델에서 피드 포워드 루프의 풍부함의 변동은 피드 포워드 루프의 농축이 [24]진화의 부작용임을 시사할 수 있다.유전자 조절 네트워크 진화의 또 다른 모델에서는 유전자 복제와 유전자 삭제 빈도의 비율이 네트워크 토폴로지에 큰 영향을 미친다.특정 비율은 피드포워드 루프의 농후화로 이어지고 계층적 규모의 자유 네트워크의 특징을 보여주는 네트워크를 만든다.일관성 있는 형식 1피드 포워드 루프의 드 새로운 진화 computationally 선택에 대한 반응에서 적응 진화를 지원하는 짧은 불요 신호를 제거해 그들의 가설 기능지만,non-idealized의 소음을, 다른 위상과 피드 포워드 규제의dynamics-based에 받았습니다 증명되었습니다.[25]

세균조절망

규제 네트워크는 박테리아가 [26][27]지구상의 거의 모든 환경적 틈새에 적응할 수 있게 해준다.DNA, RNA, 단백질 및 대사물을 포함한 다양한 유형의 분자 간의 상호작용 네트워크는 유전자 발현 조절을 달성하기 위해 박테리아에 의해 이용된다.박테리아에서 규제 네트워크의 주요 기능은 환경 변화(예: 영양 상태 및 환경 스트레스)[28]에 대한 반응을 제어하는 것입니다.복잡한 네트워크 구성을 통해 미생물은 여러 환경 [26]신호를 조정하고 통합할 수 있습니다.

모델링

결합 상미분 방정식

ODE를 사용한 세포 주기 모델링의 예는 세포 모델을 참조한다.

이러한 네트워크를 구성 부품의 반응 역학을 설명하는 일련의 결합된 상미분 방정식(ODE) 또는 SDE로 모델링하는 것은 일반적입니다.규제 네트워크에N개의 노드(\ N가 t )、 ()、 、SN ( ) \ (t )는 시간 t에 하는 N N 물질의 농도를 나타냅니다.그러면 시스템의 시간적 진화는 대략적으로 설명될 수 있습니다.

여기서 {\ 는 셀에 존재하는 다른 물질의 농도에 대한 j {\의 의존성을 나타낸다.{\ 는 궁극적으로 화학적 동역학의 기본 원리 또는 이러한 예에서 도출된 간단한 표현으로부터 도출된다.미카엘리스-멘텐 효소 동역학.따라서 {\의 함수 형태는 보통 실제 분자 역학의 안사츠 역할을 하는 저차 다항식 또는 힐 함수로 선택된다.그런 다음 비선형 역학의 수학을 사용하여 이러한 모델을 연구한다.반응 속도 상수 및 민감도와 같은 시스템 고유 정보는 상수 [29]매개변수로 인코딩됩니다.

시스템의 고정점을 해결하면 다음과 같이 됩니다.

jj에 대해 이론적으로 지속 가능한 단백질과 mRNA의 (아마도) 농도 프로파일을 얻을 수 있다.따라서 운동방정식의 정상상태는 잠재적 셀 타입에 대응하고, 위의 방정식에 대한 진동해는 자연적으로 순환 셀 타입에 대응한다.이러한 흡인체의 수학적 안정성은 보통 임계점에서 더 높은 유도체의 신호로 특징지어질 수 있으며, 그 후 농도 프로파일의 생화학적 안정성과 일치한다.방정식의 임계점과 분기는 작은 상태 또는 매개 변수 섭동이 시스템을 몇 가지 안정적인 분화 운명 중 하나로 전환할 수 있는 임계 셀 상태에 해당합니다.궤적은 생물학적 경로의 전개와 단기 생물학적 사건에 대한 방정식의 과도성에 해당한다.보다 수학적인 논의는 비선형성, 동적 시스템, 분기 이론 및 카오스 이론에 대한 문서를 참조하십시오.

부울 네트워크

주요 기사:부울 네트워크

다음 예시는 부울 네트워크가 GRN을 유전자 생성물(출력) 및 GRN에 영향을 주는 환경 물질(입력)과 함께 모델링하는 방법을 보여 줍니다.Stuart Kauffman은 Boolean 네트워크의 은유를 사용하여 유전자 조절 [30][31]네트워크를 모델링한 최초의 생물학자 중 하나였다.

  1. 각 유전자, 각 입력 및 각 출력은 두 노드 사이에 인과관계가 있는 경우에만 한 노드에서 다른 노드로 화살표가 있는 유도 그래프로 표현된다.
  2. 그래프의 각 노드는 on 또는 off의 두 가지 상태 중 하나입니다.
  3. 유전자의 경우, "on"은 발현되는 유전자에 해당하고, 입력과 출력의 경우 "off"는 존재하는 물질에 해당합니다.
  4. 시간은 개별 단계로 진행되는 것으로 보입니다.각 단계에서 노드의 새로운 상태는 화살표가 가리키는 노드의 이전 상태의 부울 함수이다.

시뮬레이션 결과를 시계열 관측치와 비교하여 모델의 유효성을 테스트할 수 있습니다.부울 네트워크 모델의 부분 검증은 각각 [32]모델의 노드인2개의 특정 문자 변환 요인 간의 아직 알려지지 않은 규제 접속의 예측 존재를 테스트하는 것으로도 할 수 있습니다.

연속 네트워크

GRN의 연속 네트워크 모델은 위에서 설명한 부울 네트워크의 확장입니다.노드는 여전히 유전자 발현에 대한 조절적 영향을 나타내며 그들 사이의 연결을 나타냅니다.생물학적 시스템의 유전자는 연속적인 활동 수준의 범위를 나타내며 연속적인 표현을 사용하면 부울 모델에 [33]존재하지 않는 유전자 조절 네트워크의 몇 가지 특성을 포착할 수 있다는 주장이 제기되어 왔다.이러한 접근법의 대부분은 노드에 대한 입력이 요약되고 그 결과가 예를 들어 [34]Sigmoid 기능에 대한 입력으로 기능하기 때문에 인공 신경망과 유사하지만, 단백질은 종종 시너지,[35] 즉 비선형 방식으로 유전자 발현을 제어한다.그러나, 현재는 노드에 대한 입력의 그룹화를 가능하게 하는 연속적인 네트워크[36] 모델이 있어, 다른 레벨의 규제를 실현하고 있습니다.이 모델은 형식적으로 고차 반복 신경망에 가깝다.세포 분화와[37] 다세포 형태 [38]형성의 진화를 모방하기 위해서도 같은 모델이 사용되었습니다.

확률적 유전자 네트워크

최근의 실험[39] 결과는 유전자 발현이 확률적 과정이라는 것을 보여주었다.따라서, Arkin 등의 연구 [41]이후 많은 작가들이 확률적 형식주의를 사용하고 있다.팀 가드너와 짐 콜린스의 유전자 전환 스위치와 같은 단일 유전자[42] 발현과 작은 합성 유전자 [43][44]네트워크에 대한 연구는 표현형 가변성과 유전자 발현 확률성에 대한 추가 실험 데이터를 제공했다.유전자 발현 확률 모델의 첫 번째 버전은 즉각적인 반응만을 포함하고 길레스피 [45]알고리즘에 의해 추진되었다.

유전자 전사와 같은 일부 과정은 많은 반응을 수반하고 한 단계에서 순간 반응으로 정확하게 모델링할 수 없기 때문에, 전체 과정이 [46]완료되는 데 걸리는 시간을 설명하기 위해 이러한 반응을 단일 단계 다중 지연 반응으로 모델링하는 것이 제안되었다.

여기서부터 GRN을 생성할 수 있는 일련의 반응이[47] 제안되었다.그런 다음 여러 시간 지연 반응을 시뮬레이션할 수 있는 수정된 Gilespie 알고리즘을 사용하여 시뮬레이션합니다(각 제품이 "완제품"으로 시스템에 출시되는 시기를 결정하는 시간 지연을 제공하는 화학 반응).

예를 들어 유전자의 기본 전사는 다음과 같은 단일 단계 반응으로 나타낼 수 있다(RNAP은 RNA 중합효소, RBS는 RNA 리보솜 결합 부위, Pro는 i 유전자 i의 프로모터 영역).

게다가, 유전자 발현에서의 잡음, 유전자가 바뀔 수 있는 속도, 그리고 그들의 기능과 관련된 대사 비용 사이에는 균형이 있는 것으로 보인다.좀 더 구체적으로 말하면, 주어진 대사 비용 수준에 대해 소음과 처리 속도 사이에 최적의 균형이 존재하며, 대사 비용을 증가시키면 속도-소음 [48][49][50]균형이 개선된다.

최근 연구는 전사 및 번역이 다중 시간 지연 이벤트로 모델링되고 그 역학이 다중 시간 지연 이벤트를 처리할 수 있는 확률 시뮬레이션 알고리즘(SSA)에 의해 구동되는 GRN을 모델링할 수 있는 시뮬레이터(SGNSim, Stochastic Gene Networks Simulator)[51]를 제안했다.시간 지연은 여러 분포와 복잡한 함수 또는 물리적 모수에서 반응 속도를 도출할 수 있습니다.SGNSim은 토폴로지 등의 사용자 정의 파라미터 세트 내에서 GRN 앙상블을 생성할 수 있습니다.또한 특정 GRN 및 화학 반응 시스템을 모델링하는 데도 사용할 수 있습니다.유전자 결실, 유전자 과잉 발현, 삽입, 프레임 이동 돌연변이와 같은 유전적 동요도 모델링할 수 있습니다.

GRN은 원하는 토폴로지를 가진 그래프에서 생성되며, 도 단위 및 도 단위 분포를 적용합니다.유전자 프로모터 활성은 입력, 모노머 형태 또는 멀티머로 결합되어 직접 또는 간접으로 설정되는 다른 유전자 발현 산물에 의해 영향을 받는다.다음으로 각 직접 입력은 오퍼레이터 사이트에 할당되며, 간접 입력이 대상이 되는 동안 서로 다른 전사 계수가 동일한 오퍼레이터 사이트에 대해 경쟁할 수 있는지 여부를 결정할 수 있다.마지막으로 각 유전자에 기능이 할당되어 전사인자의 조합(촉진제 상태)에 대한 유전자의 반응을 정의한다.전달 기능(즉, 유전자가 입력의 조합에 반응하는 방법)은 원하는 대로 프로모터 상태의 각 조합에 할당될 수 있다.

다른 최근의 연구에서는 합성 생물학 응용에 초점을 맞춘 유전자 조절 네트워크의 멀티스케일 모델이 개발되었다.유전자 조절 네트워크의 전사, 번역, 조절 및 유도에서 모든 생체 분자 상호작용을 모델링하여 합성 시스템의 [52]설계를 안내하는 시뮬레이션이 사용되었습니다.

예측

다른 연구들은 유전자 조절 네트워크에서의 유전자 발현 수준을 예측하는 데 초점을 맞추고 있다.유전자 조절 네트워크를 모델링하는 데 사용되는 접근방식은 해석할 수 있도록 제한되었으며, 결과적으로 네트워크의 일반적으로 단순화된 버전이다.예를 들어 Boolean 네트워크는 단순성과 노이즈가 많은 데이터를 처리할 수 있지만 유전자의 바이너리 표현을 통해 데이터 정보를 잃어버리기 때문에 사용되어 왔습니다.또한 인공신경망은 해석할 수 있도록 숨겨진 층을 사용하지 않으므로 데이터 내의 고차 상관관계를 모델링할 수 없다.해석할 수 있도록 제약되지 않는 모형을 사용하면 보다 정확한 모형을 생성할 수 있습니다.유전자 발현을 더 정확하게 예측할 수 있는 것은 약물이 유전자 시스템에 어떻게 영향을 미치는지뿐만 아니라 어떤 유전자가 어떤 과정에서 상호 연관되어 있는지를 알아내는 방법을 제공한다.이는 최고의 예측 알고리즘을 [54]위한 경쟁을 촉진하는 DREAM 경쟁에[53] 의해 장려되었습니다.다른 최근의 연구들은 숨겨진 [55]층이 있는 인공 신경망을 사용했다.

적용들

다발성 경화증

주요 기사:다발성 경화증

다발성 경화증에는 RRMS(Relapsing-remiting), Primary Progressive(PPMS), Secondary Progressive(SPMS)의 3가지 클래스가 있습니다.GRN(Gen Regulatory Network)은 이들 3가지 다발성 경화증 [56]클래스 전체에서 질병 메커니즘을 이해하는 데 중요한 역할을 합니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ Latchman DS (September 1996). "Inhibitory transcription factors". The International Journal of Biochemistry & Cell Biology. 28 (9): 965–74. doi:10.1016/1357-2725(96)00039-8. PMID 8930119.
  2. ^ Lee TI, Rinaldi NJ, Robert F, Odom DT, Bar-Joseph Z, Gerber GK, et al. (October 2002). "Transcriptional regulatory networks in Saccharomyces cerevisiae". Science. Young Lab. 298 (5594): 799–804. Bibcode:2002Sci...298..799L. doi:10.1126/science.1075090. PMID 12399584. S2CID 4841222.
  3. ^ Davidson E, Levin M (April 2005). "Gene regulatory networks". Proceedings of the National Academy of Sciences of the United States of America. 102 (14): 4935. Bibcode:2005PNAS..102.4935D. doi:10.1073/pnas.0502024102. PMC 556010. PMID 15809445.
  4. ^ Leitner F, Krallinger M, Tripathi S, Kuiper M, Lægreid A, Valencia A (July 2013). "Mining cis-regulatory transcription networks from literature". Proceedings of BioLINK SIG 2013: 5–12.
  5. ^ Azpeitia E, Muñoz S, González-Tokman D, Martínez-Sánchez ME, Weinstein N, Naldi A, Álvarez-Buylla ER, Rosenblueth DA, Mendoza L (February 2017). "The combination of the functionalities of feedback circuits is determinant for the attractors' number and size in pathway-like Boolean networks". Scientific Reports. 7: 42023. Bibcode:2017NatSR...742023A. doi:10.1038/srep42023. PMC 5301197. PMID 28186191.
  6. ^ Banf, Michael; Rhee, Seung Y. (January 2017). "Computational inference of gene regulatory networks: Approaches, limitations and opportunities". Biochimica et Biophysica Acta (BBA) - Gene Regulatory Mechanisms. 1860 (1): 41–52. doi:10.1016/j.bbagrm.2016.09.003. ISSN 1874-9399. PMID 27641093.
  7. ^ Kumar V, Muratani M, Rayan NA, Kraus P, Lufkin T, Ng HH, Prabhakar S (July 2013). "Uniform, optimal signal processing of mapped deep-sequencing data". Nature Biotechnology. 31 (7): 615–22. doi:10.1038/nbt.2596. PMID 23770639.
  8. ^ a b Barabási AL, Oltvai ZN (February 2004). "Network biology: understanding the cell's functional organization". Nature Reviews. Genetics. 5 (2): 101–13. doi:10.1038/nrg1272. PMID 14735121. S2CID 10950726.
  9. ^ Wagner GP, Zhang J (March 2011). "The pleiotropic structure of the genotype–phenotype map: the evolvability of complex organisms". Nature Reviews. Genetics. 12 (3): 204–13. doi:10.1038/nrg2949. PMID 21331091. S2CID 8612268.
  10. ^ Leclerc RD (August 2008). "Survival of the sparsest: robust gene networks are parsimonious". Molecular Systems Biology. 4 (1): 213. doi:10.1038/msb.2008.52. PMC 2538912. PMID 18682703.
  11. ^ a b Jukam D, Xie B, Rister J, Terrell D, Charlton-Perkins M, Pistillo D, Gebelein B, Desplan C, Cook T (October 2013). "Opposite feedbacks in the Hippo pathway for growth control and neural fate". Science. 342 (6155): 1238016. doi:10.1126/science.1238016. PMC 3796000. PMID 23989952.
  12. ^ Hoyos E, Kim K, Milloz J, Barkoulas M, Pénigault JB, Munro E, Félix MA (April 2011). "Quantitative variation in autocrine signaling and pathway crosstalk in the Caenorhabditis vulval network". Current Biology. 21 (7): 527–38. doi:10.1016/j.cub.2011.02.040. PMC 3084603. PMID 21458263.
  13. ^ Shen-Orr SS, Milo R, Mangan S, Alon U (May 2002). "Network motifs in the transcriptional regulation network of Escherichia coli". Nature Genetics. 31 (1): 64–8. doi:10.1038/ng881. PMID 11967538. S2CID 2180121.
  14. ^ Lee TI, Rinaldi NJ, Robert F, Odom DT, Bar-Joseph Z, Gerber GK, Hannett NM, Harbison CT, Thompson CM, Simon I, Zeitlinger J, Jennings EG, Murray HL, Gordon DB, Ren B, Wyrick JJ, Tagne JB, Volkert TL, Fraenkel E, Gifford DK, Young RA (October 2002). "Transcriptional regulatory networks in Saccharomyces cerevisiae". Science. 298 (5594): 799–804. Bibcode:2002Sci...298..799L. doi:10.1126/science.1075090. PMID 12399584. S2CID 4841222.
  15. ^ a b Boyle AP, Araya CL, Brdlik C, Cayting P, Cheng C, Cheng Y, et al. (August 2014). "Comparative analysis of regulatory information and circuits across distant species". Nature. 512 (7515): 453–6. Bibcode:2014Natur.512..453B. doi:10.1038/nature13668. PMC 4336544. PMID 25164757.
  16. ^ Conant GC, Wagner A (July 2003). "Convergent evolution of gene circuits". Nature Genetics. 34 (3): 264–6. doi:10.1038/ng1181. PMID 12819781. S2CID 959172.
  17. ^ Mangan S, Alon U (October 2003). "Structure and function of the feed-forward loop network motif". Proceedings of the National Academy of Sciences of the United States of America. 100 (21): 11980–5. Bibcode:2003PNAS..10011980M. doi:10.1073/pnas.2133841100. PMC 218699. PMID 14530388.
  18. ^ Goentoro L, Shoval O, Kirschner MW, Alon U (December 2009). "The incoherent feedforward loop can provide fold-change detection in gene regulation". Molecular Cell. 36 (5): 894–9. doi:10.1016/j.molcel.2009.11.018. PMC 2896310. PMID 20005851.
  19. ^ Mangan S, Itzkovitz S, Zaslaver A, Alon U (March 2006). "The incoherent feed-forward loop accelerates the response-time of the gal system of Escherichia coli". Journal of Molecular Biology. 356 (5): 1073–81. CiteSeerX 10.1.1.184.8360. doi:10.1016/j.jmb.2005.12.003. PMID 16406067.
  20. ^ Mangan S, Zaslaver A, Alon U (November 2003). "The coherent feedforward loop serves as a sign-sensitive delay element in transcription networks". Journal of Molecular Biology. 334 (2): 197–204. CiteSeerX 10.1.1.110.4629. doi:10.1016/j.jmb.2003.09.049. PMID 14607112.
  21. ^ Goentoro L, Kirschner MW (December 2009). "Evidence that fold-change, and not absolute level, of beta-catenin dictates Wnt signaling". Molecular Cell. 36 (5): 872–84. doi:10.1016/j.molcel.2009.11.017. PMC 2921914. PMID 20005849.
  22. ^ Kvitek DJ, Sherlock G (November 2013). "Whole genome, whole population sequencing reveals that loss of signaling networks is the major adaptive strategy in a constant environment". PLOS Genetics. 9 (11): e1003972. doi:10.1371/journal.pgen.1003972. PMC 3836717. PMID 24278038.
  23. ^ Lynch M (October 2007). "The evolution of genetic networks by non-adaptive processes". Nature Reviews. Genetics. 8 (10): 803–13. doi:10.1038/nrg2192. PMID 17878896. S2CID 11839414.
  24. ^ Cordero OX, Hogeweg P (October 2006). "Feed-forward loop circuits as a side effect of genome evolution". Molecular Biology and Evolution. 23 (10): 1931–6. doi:10.1093/molbev/msl060. PMID 16840361.
  25. ^ Xiong, Kun; Lancaster, Alex K.; Siegal, Mark L.; Masel, Joanna (3 June 2019). "Feed-forward regulation adaptively evolves via dynamics rather than topology when there is intrinsic noise". Nature Communications. 10 (1): 2418. Bibcode:2019NatCo..10.2418X. doi:10.1038/s41467-019-10388-6. PMC 6546794. PMID 31160574.
  26. ^ a b Filloux AA, ed. (2012). Bacterial Regulatory Networks. Caister Academic Press. ISBN 978-1-908230-03-4.
  27. ^ Gross R, Beier D, eds. (2012). Two-Component Systems in Bacteria. Caister Academic Press. ISBN 978-1-908230-08-9.
  28. ^ Requena JM, ed. (2012). Stress Response in Microbiology. Caister Academic Press. ISBN 978-1-908230-04-1.
  29. ^ Chu D, Zabet NR, Mitavskiy B (April 2009). "Models of transcription factor binding: sensitivity of activation functions to model assumptions" (PDF). Journal of Theoretical Biology. 257 (3): 419–29. Bibcode:2009JThBi.257..419C. doi:10.1016/j.jtbi.2008.11.026. PMID 19121637.
  30. ^ Kauffman SA (1993). The Origins of Order. ISBN 978-0-19-505811-6.
  31. ^ Kauffman SA (March 1969). "Metabolic stability and epigenesis in randomly constructed genetic nets". Journal of Theoretical Biology. 22 (3): 437–67. Bibcode:1969JThBi..22..437K. doi:10.1016/0022-5193(69)90015-0. PMID 5803332.
  32. ^ Lovrics A, Gao Y, Juhász B, Bock I, Byrne HM, Dinnyés A, Kovács KA (November 2014). "Boolean modelling reveals new regulatory connections between transcription factors orchestrating the development of the ventral spinal cord". PLOS ONE. 9 (11): e111430. Bibcode:2014PLoSO...9k1430L. doi:10.1371/journal.pone.0111430. PMC 4232242. PMID 25398016.
  33. ^ Vohradsky J (September 2001). "Neural model of the genetic network". The Journal of Biological Chemistry. 276 (39): 36168–73. doi:10.1074/jbc.M104391200. PMID 11395518.
  34. ^ Geard N, Wiles J (2005). "A gene network model for developing cell lineages". Artificial Life. 11 (3): 249–67. CiteSeerX 10.1.1.1.4742. doi:10.1162/1064546054407202. PMID 16053570. S2CID 8664677.
  35. ^ Schilstra MJ, Bolouri H (2 January 2002). "Modelling the Regulation of Gene Expression in Genetic Regulatory Networks". Biocomputation group, University of Hertfordshire. Archived from the original on 13 October 2007.
  36. ^ Knabe JF, Nehaniv CL, Schilstra MJ, Quick T (2006). "Evolving Biological Clocks using Genetic Regulatory Networks". Proceedings of the Artificial Life X Conference (Alife 10). MIT Press. pp. 15–21. CiteSeerX 10.1.1.72.5016.
  37. ^ Knabe JF, Nehaniv CL, Schilstra MJ (2006). "Evolutionary Robustness of Differentiation in Genetic Regulatory Networks". Proceedings of the 7th German Workshop on Artificial Life 2006 (GWAL-7). Berlin: Akademische Verlagsgesellschaft AKA. pp. 75–84. CiteSeerX 10.1.1.71.8768.
  38. ^ Knabe JF, Schilstra MJ, Nehaniv CL (2008). "Evolution and Morphogenesis of Differentiated Multicellular Organisms: Autonomously Generated Diffusion Gradients for Positional Information" (PDF). Artificial Life XI: Proceedings of the Eleventh International Conference on the Simulation and Synthesis of Living Systems. MIT Press.
  39. ^ Elowitz MB, Levine AJ, Siggia ED, Swain PS (August 2002). "Stochastic gene expression in a single cell" (PDF). Science. 297 (5584): 1183–6. Bibcode:2002Sci...297.1183E. doi:10.1126/science.1070919. PMID 12183631. S2CID 10845628.
  40. ^ Blake WJ, KAErn M, Cantor CR, Collins JJ (April 2003). "Noise in eukaryotic gene expression". Nature. 422 (6932): 633–7. Bibcode:2003Natur.422..633B. doi:10.1038/nature01546. PMID 12687005. S2CID 4347106.
  41. ^ Arkin A, Ross J, McAdams HH (August 1998). "Stochastic kinetic analysis of developmental pathway bifurcation in phage lambda-infected Escherichia coli cells". Genetics. 149 (4): 1633–48. doi:10.1093/genetics/149.4.1633. PMC 1460268. PMID 9691025.
  42. ^ Raser JM, O'Shea EK (September 2005). "Noise in gene expression: origins, consequences, and control". Science. 309 (5743): 2010–3. Bibcode:2005Sci...309.2010R. doi:10.1126/science.1105891. PMC 1360161. PMID 16179466.
  43. ^ Elowitz MB, Leibler S (January 2000). "A synthetic oscillatory network of transcriptional regulators". Nature. 403 (6767): 335–8. Bibcode:2000Natur.403..335E. doi:10.1038/35002125. PMID 10659856. S2CID 41632754.
  44. ^ Gardner TS, Cantor CR, Collins JJ (January 2000). "Construction of a genetic toggle switch in Escherichia coli". Nature. 403 (6767): 339–42. Bibcode:2000Natur.403..339G. doi:10.1038/35002131. PMID 10659857. S2CID 345059.
  45. ^ Gillespie DT (1976). "A general method for numerically simulating the stochastic time evolution of coupled chemical reactions". J. Comput. Phys. 22 (4): 403–34. Bibcode:1976JCoPh..22..403G. doi:10.1016/0021-9991(76)90041-3.
  46. ^ Roussel MR, Zhu R (December 2006). "Validation of an algorithm for delay stochastic simulation of transcription and translation in prokaryotic gene expression". Physical Biology. 3 (4): 274–84. Bibcode:2006PhBio...3..274R. doi:10.1088/1478-3975/3/4/005. PMID 17200603.
  47. ^ Ribeiro A, Zhu R, Kauffman SA (November 2006). "A general modeling strategy for gene regulatory networks with stochastic dynamics". Journal of Computational Biology. 13 (9): 1630–9. doi:10.1089/cmb.2006.13.1630. PMID 17147485. S2CID 6629364.
  48. ^ Zabet NR, Chu DF (June 2010). "Computational limits to binary genes". Journal of the Royal Society, Interface. 7 (47): 945–54. doi:10.1098/rsif.2009.0474. PMC 2871807. PMID 20007173.
  49. ^ Chu DF, Zabet NR, Hone AN (May–June 2011). "Optimal parameter settings for information processing in gene regulatory networks" (PDF). Bio Systems. 104 (2–3): 99–108. doi:10.1016/j.biosystems.2011.01.006. PMID 21256918.
  50. ^ Zabet NR (September 2011). "Negative feedback and physical limits of genes". Journal of Theoretical Biology. 284 (1): 82–91. arXiv:1408.1869. Bibcode:2011JThBi.284...82Z. doi:10.1016/j.jtbi.2011.06.021. PMID 21723295. S2CID 14274912.
  51. ^ Ribeiro AS, Lloyd-Price J (March 2007). "SGN Sim, a stochastic genetic networks simulator". Bioinformatics. 23 (6): 777–9. doi:10.1093/bioinformatics/btm004. PMID 17267430.
  52. ^ Kaznessis YN (November 2007). "Models for synthetic biology". BMC Systems Biology. 1: 47. doi:10.1186/1752-0509-1-47. PMC 2194732. PMID 17986347.
  53. ^ "The DREAM Project". Columbia University Center for Multiscale Analysis Genomic and Cellular Networks (MAGNet).
  54. ^ Gustafsson M, Hörnquist M (February 2010). "Gene expression prediction by soft integration and the elastic net-best performance of the DREAM3 gene expression challenge". PLOS ONE. 5 (2): e9134. Bibcode:2010PLoSO...5.9134G. doi:10.1371/journal.pone.0009134. PMC 2821917. PMID 20169069.
  55. ^ Smith MR, Clement M, Martinez T, Snell Q (2010). "Time Series Gene Expression Prediction using Neural Networks with Hidden Layers" (PDF). Proceedings of the 7th Biotechnology and Bioinformatics Symposium (BIOT 2010). pp. 67–69.
  56. ^ Gnanakkumaar, Perumal; Murugesan, Ram; Ahmed, Shiek S. S. J. (4 September 2019). "Gene Regulatory Networks in Peripheral Mononuclear Cells Reveals Critical Regulatory Modules and Regulators of Multiple Sclerosis". Scientific Reports. 9 (1): 12732. Bibcode:2019NatSR...912732G. doi:10.1038/s41598-019-49124-x. PMC 6726613. PMID 31484947.

추가 정보

외부 링크