가우스 네트워크 모델

가우스 네트워크 모델(GNM)은 생물학적 고분자를 탄성 질량 스프링 네트워크로 표현하여 장기간 대규모 역학의 기계적 측면을 연구, 이해 및 특성화합니다.이 모델은 단일 도메인으로 구성된 효소 같은 작은 단백질부터 리보솜이나 바이러스 캡시드와 같은 큰 고분자 조립체까지 광범위한 응용 분야를 가지고 있다.단백질 도메인 역학은 다수의 분자 인식 및 세포 신호 전달 과정에서 중요한 역할을 합니다.본질적으로 무질서한 유연한 링커 도메인으로 연결된 단백질 도메인은 단백질 도메인 역학을 통해 장거리 알로스테리를 유도한다.결과 동적 모드는 일반적으로 전체 단백질 또는 개별 도메인의 정적 구조에서 예측할 수 없다.

가우스 네트워크 모델은 생물학적 분자를 연구하기 위한 최소주의적이고 거친 접근법이다.단백질은 아미노산 잔기의 α-탄소에 대응하는 노드에 의해 나타난다.마찬가지로 DNA 및 RNA 구조는 각 뉴클레오티드에 대해 1개에서 3개의 노드로 표현된다.모형은 고조파 근사치를 사용하여 교호작용을 모형화합니다.이러한 조잡한 표현으로 계산 비용이 저렴해집니다.

분자 수준에서 효소의 촉매 활성과 같은 많은 생물학적 현상은 나노에서 밀리초의 시간 범위 내에서 발생합니다.분자역학 시뮬레이션과 같은 모든 원자 시뮬레이션 기술은 시스템의 크기와 접근 가능한 계산 자원에 따라 마이크로초 궤적 길이에 도달하는 경우가 거의 없습니다.GNM 또는 일반적으로 Elastic Network(EN; 탄성 네트워크) 모델의 컨텍스트에서의 정상 모드 분석은 고분자의 장기 기능적 동적 거동에 대한 통찰력을 제공합니다.여기서 모델은 원자상세를 희생하면서 생체분자의 고유상태 기능운동을 포착한다.이 모델에서 얻은 추론은 원자 상세 시뮬레이션 기법을 보완한다.

탄성 질량 및 스프링 네트워크에 기반한 단백질 역학의 또 다른 모델은 이방성 네트워크 모델입니다.

가우스 네트워크 모델 이론

가우스 네트워크 모델은 1997년 ^[1][2]바하르, 아틸간, 할릴로글루 및 어맨에 의해 제안되었습니다.GNM은 보통 일반 모드 분석을 사용하여 분석되며, 각 구조에 대한 분석 공식과 고유한 솔루션을 제공합니다.GNM 노멀 모드 분석은 Flory와 Rouse^[4] 모델의 탄성 이론의 영향을 받고 움직임의 3차원 방향성을 고려하지 않는다는 점에서 다른 노멀 모드 분석과 다르다.

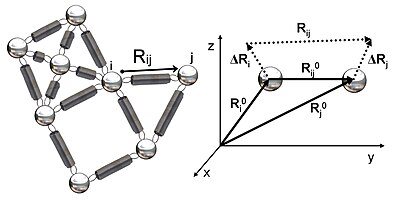
탄성망으로서의 구조 표현

그림 2는 GNM에서 연구된 탄성 네트워크의 개략도를 보여준다. 금속 비즈는 이 가우스 네트워크의 노드(단백질 잔존물)를 나타내며 스프링은 노드 간의 연결(잔기 간 공유 및 비공유 상호작용)을 나타낸다.노드 i와 j는 그림 2에 평형위치⁰_i 벡터⁰_j R과 R, 평형거리⁰_ij 벡터 R, 순간변동 벡터 δR_ij, δR, 순간거리_ij 벡터 R을 나타낸다.이들 노드의 순간 위치 벡터는 R 및_j R로_i 정의된다.잔차 i의 평형위치 벡터와 순간위치 벡터의 차이는 순간변동 벡터 δR_i = R_i - R이므로⁰_i 노드 i와 j의 순간변동 벡터는 δR_ij = δR_ji - δR_ij⁰_ij = R - R - R로 표현된다.

가우스 네트워크의 잠재력

δR의_i 관점에서 네트워크의 잠재 에너지는 다음과 같습니다.

${\displaystyle V_{GNM}=rfrac {{i,j}^{N}(\sum_{i}-\Delta R_{i}^2}\right)=rfrac {\sum {i}{2}}\left[\sum_i,j}{Delta R_Delta R}$

여기서 δ는 모든 스프링에 대한 힘의 상수 균일성이고 δ는_ij 잔류간 접점의 키르히호프(또는 연결성) 매트릭스의 ij번째 요소이며 다음과 같이 정의됩니다.

${\displaystyle \Gamma _{ij}=\left\{\mbox}-1,&{\mbox{if}}i\neq j&{\mbox{및}}R_{ij}\leq r_{c}\0,&{\mbox}{\mbox}_j}I}$

r은_c 공간적 상호작용에 대한 차단 거리이며 아미노산 쌍(α-탄소로 표현됨)의 경우 7 o로 간주된다.

변동 벡터 δR의_i X, Y, Z 성분을 δX^T = [δX₁ δX₂ .....]로 표현한다.δX_N 、 δY^T₁ = [ δY₂ 、 ... 。δY_N^T = [ δZ₁ δZ₂ .. ]δZ_N] 위의 방정식은 다음과 같이 단순화됩니다.

$({displaystyle V_{GNM}=gamfrac {Delta X^{T}\Gamma \Delta X+\Delta Y^{T}\Gamma \Delta Z^{T})$

통계역학 기초

GNM에서 모든 변동의 확률분포 P(δR)는 등방성이다.

$\displaystyle P(\Delta R)=P(\Delta X,\Delta Y,\Delta Z)=p(\Delta X)p(\Delta Y)p(\Delta Z)}$

및 가우스

$\displaystyle p(\Delta X)\propto \exp \left\{-\frac {gamma }{2k_{B}T}}\Delta X^{T}\Gamma \Delta X\right\}=\exp \left \{-{\frac {1}{2}\left(\Delta X^{T}\left({\frac {k_{B})T}{\gamma }}\Gamma^{-1}\right)^{-1}\Delta X\right\}$

여기서_B k는 볼츠만 상수, T는 절대 온도이다. p(δY)와 p(δZ)는 비슷하게 표현된다.랜덤 가변 벡터 x, 평균 벡터 μ 및 공분산 행렬 δ를 갖는 N차원 가우스 확률 밀도 함수는 다음과 같습니다.

${\displaystyle W(x,\mu,\Sigma)=black {1}{\sigmart {(2\pi)^{N}\exp \left\{-{\frac {1}{2}}{(x-\mu)^2}}T}\Sigma^{-1}(x-\mu)\right\}$

${\displaystyle \sqrt{(}}$ ${\displaystyle \sqrt{2^{}}}$ ${\displaystyle \sqrt{{}^{}}}$ ) N${\displaystyle \sqrt{}}{\displaystyle \sqrt{\sigma {}^{}\mathrm{}}}$ { \ $displaystyle${ \ $sqrt${ ($2$ \ pi )^{ $N }$ \ $Sigma }}$ 은 분포를 정규화하고$$ σ 는 공분산 행렬의 결정식입니다.

가우스 분포와 유사하게 δX^T = [δX₁ δX₂ .....]에 대한 정규 분포입니다.평형 위치 주변의 δX_N]는 다음과 같이 표현될 수 있다.

${\displaystyle p(\Delta X)=blac {1}{\displayrt {(2\pi)^{N}{\flac {k_{B}T} {\gamma }} \Gamma ^{-1} }} \exp \left \{-{\frac {1}{2}} \left(\Delta X^{T}\left({\frac {k_{B})T}{\gamma }}\Gamma^{-1}\right)^{-1}\Delta X\right\}$

정규화 상수(파티션 함수_X Z)는 다음과 같습니다.

${\displaystyle Z_{X}=\int _{0}^{\infty}\exp \left\{-{\frac {1}{2}}\left(\Delta X^{T}\left({\frac {k_{B})T}{\gamma }}\Gamma^{-1}\오른쪽)^{-1}\Delta X\오른쪽)\right\}d\Delta X}$

${\displaystyle {\mathrm{여기}}^{}}$서 k ${\displaystyle \frac{}{}{}^{}}$- $(\ displaystyle {k_{$$B}$$이$ 경우 T}{\$gamma$}}\$Gamma$^{-$1}$는 공분산 행렬입니다.Z와_YZ Z는 비슷하게 표현된다.이 공식은 키르히호프 행렬의 반전을 필요로 한다.GNM에서 키르히호프 행렬의 행렬식은 0이므로 그 역수를 계산하려면 고유값 분해가 필요하다.δ는⁻¹ 0이 아닌 N-1 고유값 및 관련 고유 벡터를 사용하여 구성됩니다.p(δY) 및 p(δZ) 표현은 p(δX) 표현과 유사합니다.GNM의 모든 변동의 확률 분포는

${\displaystyle P(\Delta R)=p(\Delta X)p(\Delta Y)p(\Delta Z)=parcfrac {1}{\displayrt {(2\pi)^3N({frac {k_{B})T}{\gamma }}\Gamma ^{-1}^{3}}}\exp \left\{-{\frac {3}{2}}\left(\Delta X^{T}\left({\frac {k_{B})T}{\gamma }}\Gamma^{-1}\right)^{-1}\Delta X\right\}$

이 매스 및 스프링 시스템의 경우 위의 식에서 정규화 상수는 전체 GNM 파티션 함수 Z입니다_GNM.

${\displaystyle Z_{GNM}=Z_{X}Z_{Y}Z_{Z}=black{1}{\blackrt {(2\pi)^3N({frac {k_{B})T}{\gamma }}\Gamma^{-1}^{3}}}}$

변동 및 상관관계 기대치

잔차 변동의 기대치인 <rR_i²>(평균-제곱 변동, MSF라고도 함)와 이들의 교차 상관인 < ·R_i · >R_j>은 각각 공분산 행렬의 대각항과 대각항으로 구성할 수 있다.통계역학에 기초하여 δX에 대한 공분산 행렬은 다음과 같이 주어진다.

$\displaystyle <\Delta X\cdot\Delta X^{T}>=\int \Delta X\cdot \Delta X^{T}p(\Delta X)d\Delta X=delta frac {k_{B}T}{\gamma }}\Gamma ^{-1}$

마지막 등식은 위의 p(δX)를 삽입하고 (일반화된 가우스) 적분을 취함으로써 얻을 수 있습니다.부터,

$\displaystyle <\Delta X\cdot\Delta X^{T}>= <\Delta Y\cdot \Delta Y^{T}>= <\Delta Z\cdot \Delta Z^{T}> = flac {1}{3}} <\Delta R\cdot \Delta R^{T} >}$

<rR_i² > 및 < ·R_i · >R_j >는 다음과 같습니다.

${\displaystyle <\Delta R_{i}^{2}>=420frac {3k_{B}T}{\gamma }}(\Gamma ^{-1}_{ii})$

${\displaystyle <\Delta R_{i}\cdot \Delta R_{j}>=blac {3k_{B}T}{\gamma }}(\Gamma ^{-1}_{ij})$

모드 분해

GNM 정규 모드는 Kirchhoff 행렬의 대각선화(δ^T = U)로 구한다. 여기서 U는 δ의 고유 벡터_i u의 단일 행렬, U^T = U는⁻¹ 고유값 δ의_i 대각 행렬이다.모드의 빈도와 모양은 각각 고유값과 고유 벡터로 표시됩니다.Kirchhoff 행렬은 정의 반정의 행렬이므로 첫 번째 고유값 θ는₁ 0이며 대응하는 고유 벡터는 모든 요소가 1/µN과 같다.이것은 네트워크 모델이 변환에 불변함을 나타냅니다.

잔류물 변동 간의 교차 상관관계는 N-1 비제로 모드에 대한 합으로 다음과 같이 기술할 수 있다.

${\displaystyle <\Delta R_{i}\cdot \Delta R_{j}>=blac {3k_{B}T} {\gamma }} [U\Lambda ^{-1}U^{T}]_{ij}=blac {3k_{B}T}{\gamma}}\sum _{k=1}^{N-1}\lambda _{k}^{-1}[u_{k}u_{T}_{ij}}$

따라서 [δR_i · δR_j], 개별 모드의 기여도는 다음과 같이 표현된다.

${\displaystyle [\Delta R_{i}\cdot \Delta R_{j}_{k}=blac {3k_{B}T}{\gamma}}\lambda _{k}^{-1}[u_{k}_{i}[u_{k}]_{j}$

여기서 [u_k]_i는 u의_k ith 요소입니다.

국소 패킹 밀도의 영향

정의상 키르히호프 행렬의 대각선 요소 δ는_ii 대응하는 잔류물의 좌표수를 나타내는 GNM 내의 노드의 정도와 같다.이 수치는 특정 잔류물 주변의 국소 패킹 밀도를 측정한 값입니다.국소 패킹 밀도의 영향은 δ⁻¹ 매트릭스의 직렬 팽창으로 평가할 수 있다.δ는 δ의 대각 원소와 오프 원소를 포함한 δ = D + O 두 행렬의 합으로 쓸 수 있다.

δ⁻¹ = (D ⁻¹+ O) = [ D (I⁻¹ + DO)⁻¹ ] = (I^{−1 −1}+ DO⁻¹)D = (I⁻¹ - DO + ...))⁻¹D⁻¹ = D⁻¹ - DO⁻¹⁻¹ D + ...

이 식은 ^[5]국소 패킹 밀도가 잔류물의 예상 변동에 상당한 기여를 한다는 것을 보여줍니다.대각 행렬의 역행렬 뒤에 오는 항은 기대 변동에 대한 위치 상관의 기여입니다.

GNM 어플리케이션

평형 변동

생체 분자의 평형 변동을 실험적으로 측정할 수 있다.X선 결정학에서 각 원자의 B-인자(Debye-Waller 또는 온도 인자라고도 함)는 기본 구조에서 평형 위치 근처에서의 평균-제곱 변동을 측정하는 척도입니다.NMR 실험에서 이 측도는 서로 다른 모형 간의 평균 제곱근 차이를 계산하여 얻을 수 있습니다.원본 기사를 포함한 많은 응용 프로그램 및 출판물에서 GNM에 의해 얻어진 예상 잔류 변동은 실험적으로 측정된 고유 상태 ^[6][7]변동과 잘 일치한다는 것이 입증되었다.예를 들어 B-요인과 GNM에서 얻을 수 있는 예상잔차변동과의 관계는 다음과 같다.

${\displaystyle B_{i}=black {8\pi ^{2}}{3}<\Delta R_{i}\cdot \Delta R_{i}>=blac {8\pi ^{2}k_{B}T}{\gamma }}(\Gamma ^{-1}_{ii})$

그림 3은 세포분열주기 이중특이성 포스파타아제인 단백질 Cdc25B의 촉매 도메인에 대한 GNM 계산의 예를 나타낸다.

저속 및 고속 모드의 물리적 의미

키르히호프 행렬의 대각화는 배향 운동을 집합 모드의 스펙트럼으로 분해한다.변동 및 교차 상관의 기대값은 이러한 정규 모드를 따른 변동의 선형 조합에서 얻을 수 있습니다.각 모드의 기여도는 해당 모드의 주파수의 역순으로 스케일링됩니다.따라서 느린(저주파수) 모드가 예상되는 변동의 가장 큰 원인이 됩니다.가장 느린 몇 가지 모드를 따라, 움직임은 집단적이고 전역적이며 잠재적으로 생체 분자의 기능과 관련이 있는 것으로 나타납니다.반면 고속(고주파) 모드는 구조에서 주목할 만한 변화를 유발하지 않는 상관 없는 움직임을 나타냅니다.GNM 기반 방법은 실제 역학을 제공하지 않고 일반 ^[8]모드의 조합과 보간에 기초한 근사치만 제공합니다.이들의 적용가능성은 그 움직임이 ^[8][9]얼마나 집단적인지에 따라 크게 좌우된다.

기타 특정 응용 프로그램

가우스 네트워크 모델 및 기타 탄성 네트워크 모델이 ^[10]유용한 것으로 판명된 주요 영역이 몇 가지 있습니다.여기에는 다음이 포함됩니다.

• 스프링 비즈 기반 네트워크 모델:스프링 비드 기반 네트워크 모델에서는 스프링과 비드가 가교 네트워크의 컴포넌트로 사용됩니다.스프링은 재료 및 브리지 분자 역학(MD) 모델과 유한 요소(FE) 모델의 기계적 거동을 나타내기 위해 가교되어 있습니다(그림 5 참조).구슬은 클러스터 결합의 물질 질량을 나타냅니다.각 스프링은 단일 고분자 사슬의 일부 대신 고분자 사슬의 클러스터를 나타내기 위해 사용됩니다.이러한 단순화를 통해 여러 모델을 여러 길이 축척으로 연결할 수 있으며 시뮬레이션 효율성을 크게 개선할 수 있습니다.시뮬레이션의 각 반복 단계에서 스프링 내의 힘이 비드의 중심에 있는 노드에 가해지고 시스템 전체의 평형화된 노드 변위가 계산된다.응력 및 변형률을 구하는 기존의 FE 방법과는 달리 스프링-비드 모델은 스프링 내 노드 및 힘의 변위를 제공합니다.스프링 기반 네트워크 모델의 등가 변형률 및 변형률 에너지는 노드의 변위와 스프링 특성을 사용하여 정의 및 계산할 수 있습니다.또, 네트워크 모델로부터의 결과를 스케일 업 해, FE ^[11][12]해석을 사용해 매크로 스케일에서의 구조 응답을 얻을 수 있다.
• 유연한/강성 영역 및 단백질 영역의 분해
• 단백질, 효소 및 대규모 고분자 어셈블리의 기능적 움직임과 기능적으로 중요한 부위/잔해의 특성화
• 저분해능 구조 데이터(예: 극저온 전자 현미경^{[27][28][29][30]} 검사)의 정교화 및 역학
• 알려진^[31] 구조와 관련하여 구조 변화가 발생한 경우 X선 구조를 해결하기 위한 분자 대체
• 원자론적 모델 및 시뮬레이션과의 통합
• 접이식/접이식 경로 및 동력학 ^[34][35]조사.
• 분자 진화의 기능적 함의 주석

웹 서버

실제로 두 가지 종류의 계산을 수행할 수 있습니다.첫 번째 종류(GNM 자체)는 키르히호프 ^[1][2]행렬을 사용합니다.두 번째 종류(구체적으로는 탄성 네트워크 모델 또는 이방성 네트워크 모델)는 대응하는 고조파 ^[38]스프링 세트와 관련된 헤시안 매트릭스를 사용합니다.다음 서버를 사용하여 두 가지 모델을 모두 온라인으로 사용할 수 있습니다.

GNM 서버

• iGNM: GNM을 기반으로 한 단백질 기능 동작 데이터베이스 http://ignm.ccbb.pitt.edu
• oGNM: GNM을 사용한 구조역학 온라인 계산 https://web.archive.org/web/20070516042756/http://ignm.ccbb.pitt.edu/GNM_Online_Calculation.htm

ENM/ANM 서버

• 이방성 네트워크 모델웹 서버 http://www.ccbb.pitt.edu/anm
• ElNemo: Elastic Network Model 웹 인터페이스 http://www.sciences.univ-nantes.fr/elnemo/
• AD-ENM: 탄성 네트워크 모델의 역학 분석 http://enm.lobos.nih.gov/
• WEBnm@: 단백질 정상 모드 분석용 웹 서버 http://apps.cbu.uib.no/webnma/home

기타 관련 서버

• ProDy: Python의 Application Programming Interface(API)로 GNM 및 ANM 분석과 여러 분자 구조 및 시퀀스 분석 및 시각화 도구를 통합합니다.http://prody.csb.pitt.edu
• HinggeProt:탄성 네트워크 모델 http://www.prc.boun.edu.tr/appserv/prc/hingeprot/, 또는 http://bioinfo3d.cs.tau.ac.il/HingeProt/hingeprot.html을 사용한 단백질 힌지 예측 알고리즘
• DNABindProt: 단백질의 잠재적 DNA 결합 부위를 판별하는 서버 http://www.prc.boun.edu.tr/appserv/prc/dnabindprot/
• MolMovDB: 고분자 운동 데이터베이스: http://www.molmovdb.org/

「 」를 참조해 주세요.

• 가우스 분포
• 고조파 발진기
• 후크의 법칙
• 분자역학
• 통상 모드
• 주성분 분석
• 단백질 역학
• 고무 탄성
• 통계역학

레퍼런스

주요 소스

특정 인용문