이체 문제

왼쪽: 비슷한 질량을 가진 두 물체는 양쪽 물체의 바깥쪽에 있는 공통의 중심 주위를 돌고 있으며 타원 궤도를 가지고 있다.쌍성계의 전형적인 형태이다.오른쪽:같은 중입자 중심 주위를 도는 질량의 "약간" 차이를 가진 두 물체.크기와 이러한 유형의 궤도는 명왕성-카론계(중심점이 양쪽 물체의 외부에 있음)와 지구-달계(중심점이 더 큰 물체의 내부에 있음)와 유사합니다.

고전역학에서, 2체 문제는 추상적으로 점 입자로 보이는 두 개의 거대한 물체의 움직임을 예측하는 것입니다.이 문제는 두 개체가 서로만 상호작용하는 것으로 가정합니다. 각 개체에 영향을 미치는 유일한 힘은 다른 개체에서 발생하고 다른 개체는 모두 무시됩니다.

고전적인 이체 문제의 가장 두드러진 경우는 천문학에서 위성, 행성, 별과 같은 물체의 궤도를 예측하기 위해 발생하는 중력 케이스이다.이러한 시스템의 2점 입자 모델은 유용한 통찰력과 예측을 제공할 수 있을 정도로 거의 항상 그 동작을 잘 묘사합니다.

보다 단순한 "하나의 물체" 모델인 "중심력 문제"는 한 물체를 다른 물체에 작용하는 힘의 움직이지 않는 원천으로 취급한다.그런 다음 남은 단일 이동 물체의 움직임을 예측하려고 합니다.이러한 근사치는 한 물체가 다른 물체보다 훨씬 더 질량이 클 때 유용한 결과를 얻을 수 있습니다(항성이 무거운 별 주위를 도는 가벼운 행성과 같이).

단, 일반적으로 단체근사는 디딤돌 이외에는 불필요하다.중력을 포함한 많은 힘의 경우, 이체 문제의 일반적인 버전은 한 쌍의 일체 문제로 축소될 수 있으며, 이 문제를 완전히 해결할 수 있으며, 효과적으로 사용할 수 있을 만큼 간단한 해결책을 제공할 수 있습니다.

이와는 대조적으로, 3체 문제(그리고 일반적으로 n 3 3에 대한 n체 문제)는 특별한 경우를 제외하고 첫 번째 적분 측면에서 해결할 수 없다.

중요 사례에 대한 결과

중력 및 기타 역제곱 예제

두 물체의 문제는 천문학에서 흥미로운데, 왜냐하면 천문학 물체의 쌍들은 종종 임의의 방향으로 빠르게 움직이기 때문이다. 왜냐하면 그들은 서로 크게 떨어져 있고(충돌하지 않기 위해), 그리고 심지어 더 넓게 떨어져 있기 때문이다(그래서 외부의 영향은 안전하게 무시될 수 있을 만큼 작을 것이다.).

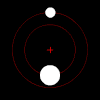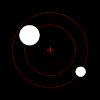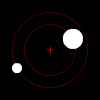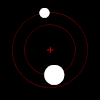
중력에 의해, 그러한 한 쌍의 물체의 각 구성원은 서로 완전히 탈출할 만큼 충분히 빠르게 움직이지 않는 한, 타원 패턴으로 서로의 질량 중심을 공전할 것이고, 이 경우 그들의 경로는 다른 평면 원뿔 단면을 따라 갈라질 것입니다.만약 한 물체가 다른 물체보다 훨씬 더 무겁다면, 그것은 공유 질량 중심을 기준으로 다른 물체보다 훨씬 덜 움직일 것입니다.질량의 상호 중심은 더 큰 물체 안에 있을 수도 있습니다.

문제에 대한 해법의 도출은 고전적인 중심력 문제 또는 케플러 문제를 참조하십시오.

원칙적으로 동일한 해결책은 중력뿐만 아니라 역제곱 법칙을 따르는 다른 매력적인 스칼라 힘장을 통해 상호작용하는 물체와 관련된 거시적 문제에 적용된다. 정전적 인력은 명백한 물리적 예다.실제로 이러한 문제는 거의 발생하지 않습니다.아마도 실험 장치나 다른 특수 장치를 제외하고는 충돌을 피하기 위해 충분히 빠르게 또는 그러한 방향으로 움직이는, 또는 주변으로부터 충분히 격리된 정전기적으로 상호작용하는 물체와 거의 마주치지 않습니다.

토크의 영향을 받는 2체 시스템의 동적 시스템은 Sturm-Liouville ^[1]방정식으로 판명되었습니다.

원자 및 아원자 입자에 적용할 수 없음

이체 모형은 물체를 점 입자로 취급하지만, 고전 역학은 거시적 규모의 시스템에만 적용됩니다.아원자 입자의 대부분의 동작은 이 기사의 기초가 되는 고전적인 가정이나 여기서의 수학을 사용하여 예측할 수 없다.

원자의 전자는 닐스 보어(Niels Bohr)의 초기 추측에 따라 원자핵을 공전하는 것으로 설명되기도 한다.하지만, 전자는 실제로 어떤 의미에서도 핵 주위를 도는 것이 아니며, 양자역학은 전자의 실제 행동을 이해하기 위해 필요하다.원자핵 주위를 도는 전자의 고전적인 2체 문제를 해결하는 것은 오해를 불러일으키고 유용한 통찰력을 많이 만들어내지 못한다.

독립된 두 가지 일체형 문제로 감소

완전한 이체 문제는 두 가지 일체의 문제로 다시 공식화함으로써 해결할 수 있습니다. 사소한 문제와 외부 전위에서의 한 입자의 움직임을 해결하는 것을 수반하는 문제.많은 일체의 문제를 정확하게 해결할 수 있기 때문에 그에 상응하는 이체 문제도 해결할 수 있다.

2체 문제에 대한 Jacobi 좌표. Jacobi 좌표는 R

{\boldsymbol {R}}={\frac {m_{1}}{M}}{\boldsymbol {x}}_{1}+{\frac {m_{2}}{M}}{\boldsymbol {x}}_{2}

{\boldsymbol {R}}={\frac {m_{1}}{M}}{\boldsymbol {x}}_{1}+{\frac {m_{2}}{M}}{\boldsymbol {x}}_{2}

{\boldsymbol {R}}={\frac {m_{1}}{M}}{\boldsymbol {x}}_{1}+{\frac {m_{2}}{M}}{\boldsymbol {x}}_{2}

M

{\boldsymbol {R}}={\frac {m_{1}}{M}}{\boldsymbol {x}}_{1}+{\frac {m_{2}}{M}}{\boldsymbol {x}}_{2}

1 +

{\boldsymbol {R}}={\frac {m_{1}}{M}}{\boldsymbol {x}}_{1}+{\frac {m_{2}}{M}}{\boldsymbol {x}}_{2}

{\boldsymbol {R}}={\frac {m_{1}}{M}}{\boldsymbol {x}}_{1}+{\frac {m_{2}}{M}}{\boldsymbol {x}}_{2}

{\boldsymbol {R}}={\frac {m_{1}}{M}}{\boldsymbol {x}}_{1}+{\frac {m_{2}}{M}}{\boldsymbol {x}}_{2}

x

{\boldsymbol {R}}={\frac {m_{1}}{M}}{\boldsymbol {x}}_{1}+{\frac {m_{2}}{M}}{\boldsymbol {x}}_{2}

({

displaystyle

{ \ bold

symbol

{

{\boldsymbol {R}}={\frac {m_{1}}{M}}{\boldsymbol {x}}_{1}+{\frac {m_{2}}{M}}{\boldsymbol {x}}_{2}

R }

= sclac

{

m _

{ m _ { m

{\boldsymbol {R}}={\frac {m_{1}}{M}}{\boldsymbol {x}}_{1}+{\frac {m_{2}}{M}}{\boldsymbol {x}}_{2}

_ {

m 1}

+ { \

bold symbol }

} {

mbold

symbol { 2 } { 2 } } } r

{\boldsymbol {R}}={\frac {m_{1}}{M}}{\boldsymbol {x}}_{1}+{\frac {m_{2}}{M}}{\boldsymbol {x}}_{2}

。

}_{

2

{\boldsymbol {r}}={\boldsymbol {x}}_{1}-{\boldsymbol {x}}_{2}

}}(

M=m_{1}+m_{2}\

=

M=m_{1}+m_{2}\

+

m2

{{

displaystyle M= m_{

1} +

m_

{2

})

}\

^[2]}.

$x$ 와₂ x를 두 물체의 벡터 위치, m과₁₂ m을 질량이라고 $하자 1$ .목표는 초기 $위치 1$ x $(t$ = $0)$ 와₂ x $(t$ = $0)$ 와 초기 $속도 1$ v $(t$ $= 0$ )와₂ v $(t$ = $0)$ 가 주어진 모든 시간 t에 대한 $궤적 1$ x $(t)$ 와₂ x $(t)$ 를 결정하는 것이다.

두 질량에 적용될 때, 뉴턴의 제2법칙은 다음과 같이 기술한다.

\mathbf {F} _{12}(\mathbf {x} _{2})=m_{1}{\ddot {\mathbf {x}} {1

(등식 1)

\mathbf {F} _{21}(\mathbf {x} _{2})=m_{2}{\dot {\mathbf {x}} _{2

(등식 2)

여기서₁₂ F는 질량 2와의 상호작용으로 인한 질량 1에 대한 힘이고₂₁ F는 질량 1과의 상호작용으로 인한 질량 2에 대한 힘이다.x 위치 벡터 위에 있는 두 개의 점은 시간과 관련된 두 번째 도함수 또는 가속도 벡터를 나타냅니다.

이 두 방정식을 더하고 빼면 독립적으로 풀 수 있는 두 가지 일체의 문제로 분리된다.방정식 (1)과 (2)를 더하면 질량 중심(중심) 운동을 설명하는 방정식이 생성됩니다.반면, 방정식 (1)에서 식 (2)을 빼면 질량 $사이$ 의 벡터 $r 1$ = $x 2$ - x가 시간에 따라 어떻게 변화하는지 설명하는 방정식이 된다.이러한 독립적인 일체 문제의 해법은 $궤적 1$ x $(t)$ 와₂ x $(t)$ 에 대한 해법을 얻기 위해 결합될 수 있다.

질량 운동 중심(1차 단신 문제)

R $(\$ 을 $\mathbf{R}$ 시스템의 질량 중심(중심) 위치로 $\mathbf {R}$ .힘 방정식 (1)과 (2)를 더하면 다음과 같은 결과가 나온다.

m_{1}{\ddot {mathbf {x}}_{1}+m_{2}{\dot {mathbf {x}}}_{2}=(m_{1}+m_{2}){\dot {mathbf {R}}=\mathbf {F}_{12}+\mathbf {F}_{21}=0

여기서 뉴턴의 제3법칙

12

F =

-F

를₂₁ 사용했고, 여기서

{\mathbf {R}}\equiv {frac {m_{1}{\dot {\mathbf {x}}_{1}+m_{2}}{\ddot {\mathbf {x}}_{2}}{m_{1}+m_{2}}}.

결과 방정식은 다음과 같습니다.

{\displaystyle\ddot\mathbf {R}}=0}

는 질량 중심의

\mathbf {v} ={\frac {dR}{dt}}

v

\mathbf {v} ={\frac {dR}{dt}}

\mathbf {v} ={\frac {dR}{dt}}

\mathbf {v} ={\frac {dR}{dt}}

\mathbf {v} ={\frac {dR}{dt}}

t

\mathbf {v} ={\frac {dR}{dt}}

{\

displaystyle \mathbf {v}

=

plac frac {dR}{

dt}}}이

\mathbf {v} ={\frac {dR}{dt}}

일정함을 나타내므로 총

운동량 1

m 1

v +

m 2 2

v도 일정함을 나타냅니다(운동량 보존).따라서 초기 위치 및 속도에서 항상 질량중심의

위치 R (

t)을 결정할 수 있다.

변위 벡터 운동(2차 단체 문제)

두 힘 방정식을 각각의 질량으로 나누고, 첫 번째 방정식에서 두 번째 방정식을 뺀 다음, 정렬하면 방정식을 얻을 수 있습니다.

({displaystyle {mathbf {r}}={1}-{\ddot {mathbf {x}}}_{2}=\left\frac {mathbf {F}_{12}}-{{1}}-{\frac {f}_2}) {m}_21}}:{m}}:{{dot}

여기서 다시 뉴턴의 제3법칙

12

F =

-F

를₂₁ 사용했고

여기

서 r은 위에서 정의한 질량 2에서 질량 1까지의 변위 벡터입니다.

두 물체에서 발생하는 두 물체 $사이$ 의 힘은 분리 r의 $함수$ 일₁ 뿐 $절대 2$ 위치 x와 x의 함수가 아니다. 그렇지 않으면, 번역 대칭이 존재하지 않을 것이고, 물리 법칙이 이곳 저곳에서 바뀌어야 할 것이다.따라서 감산 방정식은 다음과 같이 쓸 수 있습니다.

{\displaystyle\mathbf {r}}=\mathbf {F}_{12}(\mathbf {x}_{1},\mathbf {x}_{2}=\mathbf {F}(\mathbf {r})}

\mu

서

\mu

μ {\

displaystyle \mu}

는

\mu

축소된 질량입니다.

\mu = specfrac {1} {\frac {1} {m_{1}} + {\frac {1} {m_{2}} = specfrac {m_{1} m_{2}} {m_{1} + m_{2}}}.

r $(t)$ 에 대한 방정식을 푸는 것이 이체 문제의 핵심이다.해법은 F $\mathbf {F} (\mathbf {r} )$ ( $\mathbf {F} (\mathbf {r} )$ ) \ $displaystyle \mathbf {F}$ ( \ $mathbf {r}$ )로 정의되는 물체 간의 특정 힘에 따라 달라집니다 $\mathbf {F} (\mathbf {r} )$ F ( $\mathbf {F} (\mathbf {r} )$ ) \ $displaystyle \mathbf {F}$ ( \ $mathbf {r}$ )가 $\mathbf {F} (\mathbf {r} )$ 역제곱 법칙을 따르는 $\mathbf {F} (\mathbf {r} )$ 에는 케플러 문제를 참조하십시오.

$일단 R ($ t)와 $r ($ t)가 결정되면, 원래의 궤적을 얻을 수 있다.

\displaystyle \mathbf {x} _{1}(t)=\mathbf {R}(t)+{\frac {m_{2}}{m_{1}+m_{2}}}\mathbf {r}(t)}

\displaystyle \mathbf {x} _{2}(t)=\mathbf {R}(t)-{\frac {m_{1}}{m_{1}+m_{2}}}\mathbf {r}(t)}

R과 r의 정의를 이 두 방정식의 우측에 대입하여 검증할 수 있다.

2체 운동은 평면입니다.

서로에 대한 두 물체의 움직임은 항상 평면(질량 프레임의 중심)에 있습니다.

증명: 질량 중심에 대한 시스템의 선형 $운동량$ p와 각 $운동량$ L을 방정식으로 정의합니다.

\mathbf {L} =\mathbf {p} \times \mathbf {r} \times \mu \frac {d\mathbf {r} } {dt}

$여기$ 서 μ는 감소된 질량, $r$ 은₁ 상대적 $위치 2$ r - r(이것들은 질량의 중심을 원점으로 하여 둘 다 r과 $평행$ ) $각운동량$ L의 변화율은 $순토크$ N과 같다.

\mathbf {N} = flac {d\mathbf {L} } } {dt} = dot {\mathbf {r} } } \ times \ mu \ dot \ mathbf {r} }

그리고

벡터

v

와 w가 같은 방향을 가리키는 벡터 v에 대해

v

×

w

=

0인

벡터 교차곱의 속성을 사용한다.

\displaystyle \mathbf {N} \ = \ { frac { d \ mathbf { L } } { dt} = \ mathbf { r } \ times \ mathbf { F } \ , }

F

=

μ 2

dr

/ dt일 2

때.

두 입자 사이의 힘이 위치 사이의 선을 따라 작용하고 각 운동량 벡터 L이 일정(보존)하다는 가정(대부분의 물리적 힘에 해당)을 도입하면, r × $F$ = $0$ 이라는 $가정$ (보존)이 뒤따른다.따라서 변위 $벡터$ r과 그 $속$ 도 v는 항상 상수 $벡터$ L에 수직인 평면에 있다.

이체계의 에너지

$힘$ F $(r)$ 가 보수적인 경우 시스템은 전위 $에너지$ U $(r)$ 를 가지므로 총 에너지는 다음과 같이 쓸 수 있습니다.

({displaystyle E_{\text{tot}}=blac {1}{1}{1}+{1}{2}+{2}m_{2}{\dot {\mathbf {x}}}_{2}}_{2}}_{2}}_{2}}_{2}}_{2}}_{2}}_{2}}_{2}}_{2}}_{{{2}}}}_{{{{2}}}}}}}}}_{{{\dot{{{{2}}}}}}}}}}}}{{{{{{{

질량 프레임의 중심에서 운동 에너지는 가장 낮고 총 에너지는 더 작아집니다.

{{displaystyle E=matfrac {1}{2}}\mu {dot {mathbf {r}}^{2}+U(\mathbf {r})}

좌표 1

x

와₂ x는 다음과 같이 나타낼 수 있습니다.

\mathbf {x} _{1} = flac {mu } {m_{1}\mathbf {r

\mathbf {x} _{2}=-{\frac {mu }{m_{2}}\mathbf {r

에너지 E는 각 물체의 운동 에너지를 별도로 포함하는

에너지 1

E 및

E

와₂ 유사한 방식으로 관련된다.

디스플레이 스타일E_{1}&=capfrac {m_{1}}E=capfrac {1}{2}m_{1}{\dot {mathbf {x}}_{1}+{\frac {m_{1}}U(\mathbf {r}\pt}E_{2}&=capfrac {m_{2}}E=capfrac {1}{2}m_{2}{\dot {mathbf {x}}_{2}+{\frac {m_{2}}U(\mathbf {r}\pt}E_{\text{tot}}&=E_{1}+E_{2}\end{aligned}}

중앙군

많은 물리적 $문제$ 에서 힘 F $(r)$ 는 중심력이다. 즉, 그 형태이다.

\displaystyle \mathbf {F}(\mathbf {r})=F(r){\hat\mathbf {r}}

여기

서 r =

r

및

rsolution =

r / r

은 해당하는 단위 벡터입니다.다음과 같은 기능이 있습니다.

{\displaystyle\mu\mathbf {r}}={F}(r){\hat\mathbf {r}}\,}

여기서 F(r)는 인력의 경우 음수이다.

「」를 참조해 주세요.

레퍼런스

^ Luo, Siwei (22 June 2020). "The Sturm-Liouville problem of two-body system". Journal of Physics Communications. 4 (6): 061001. Bibcode:2020JPhCo...4f1001L. doi:10.1088/2399-6528/ab9c30.
^ David Betounes (2001). Differential Equations. Springer. p. 58; Figure 2.15. ISBN 0-387-95140-7.

참고 문헌

Landau LD; Lifshitz EM (1976). Mechanics (3rd. ed.). New York: Pergamon Press. ISBN 0-08-029141-4.
Goldstein H (1980). Classical Mechanics (2nd. ed.). New York: Addison-Wesley. ISBN 0-201-02918-9.

외부 링크

Eric Weisstein의 물리학 세계에서의 이체 문제

[1] Luo, Siwei (22 June 2020). "The Sturm-Liouville problem of two-body system". Journal of Physics Communications. 4 (6): 061001. Bibcode:2020JPhCo...4f1001L. doi:10.1088/2399-6528/ab9c30.

[Betounes-2] David Betounes (2001). Differential Equations. Springer. p. 58; Figure 2.15. ISBN 0-387-95140-7.

[1]

[2]

Search

이체 문제

네임스페이스

더

목차

중요 사례에 대한 결과

중력 및 기타 역제곱 예제

원자 및 아원자 입자에 적용할 수 없음

독립된 두 가지 일체형 문제로 감소

질량 운동 중심(1차 단신 문제)

변위 벡터 운동(2차 단체 문제)

2체 운동은 평면입니다.

이체계의 에너지

중앙군

「」를 참조해 주세요.

레퍼런스

참고 문헌

외부 링크

Search

이체 문제

중요 사례에 대한 결과

중력 및 기타 역제곱 예제

원자 및 아원자 입자에 적용할 수 없음

독립된 두 가지 일체형 문제로 감소

질량 운동 중심(1차 단신 문제)

변위 벡터 운동(2차 단체 문제)

2체 운동은 평면입니다.

이체계의 에너지

중앙군

「 」를 참조해 주세요.

레퍼런스

참고 문헌

외부 링크

「」를 참조해 주세요.