고조파

이 기사는 검증을 위해 추가 인용이 필요합니다. 신뢰할 수 있는 출처에 인용을 추가하여 이 기사를 개선하는 데 도움을 주세요. 출처가 없는 재료는 문제가 발생하여 제거될 수 있습니다. 출처 찾기 : "Harmonic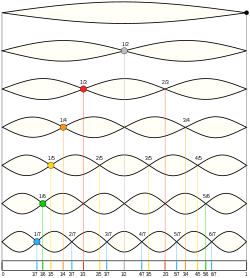" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2020년 8월) (본 템플릿 메시지 제거 방법 및 시기에 대해 알아보기)

고조파(harmonic)는 물리학, 음향학, 전기통신 분야에서 주기적 신호의 기본 주파수의 양의 정수배인 주파수를 가진 정현파입니다. 기본 주파수는 1차 고조파라고도 하며, 다른 고조파는 상위 고조파라고 합니다. 모든 고조파는 기본 주파수에서 주기적이기 때문에 고조파의 합도 그 주파수에서 주기적입니다. 고조파 세트는 고조파 시리즈를 형성합니다.

이 용어는 음악, 물리학, 음향, 전자 전력 전송, 라디오 기술 및 기타 분야를 포함한 다양한 분야에서 사용됩니다. 예를 들어 기본 주파수가 공통 AC 전원 공급 주파수인 50Hz인 경우 처음 3개의 고조파의 주파수는 100Hz(2차 고조파), 150Hz(3차 고조파), 200Hz(4차 고조파)이며 이러한 주파수를 가진 파동의 추가는 50Hz에서 주기적입니다.

n^th > 1인 특성 모드에는 진동하지 않는 노드가 있습니다. 예를 들어, 세 번째 특성 모드에는 ${\displaystyle \frac{13}{}}$ ${\$ $L$ 및 ${\displaystyle \frac{23}{}}$ ${\$ $L$에 노드가 있습니다. 여기서 L은 문자열 길이입니다. 실제로 n개의^th 특성 모드는 3의 배수가 아닌 각각의 n개의 특성 모드는 이러한 지점에 노드를 갖지 않습니다. 이러한 다른 특성 모드는 ${\displaystyle \frac{13}{}}$ ${\$ L $및$ ${\displaystyle \frac{23}{}}$ ${\$ L $위치$에서 진동합니다. 플레이어가 이러한 위치 중 하나를 부드럽게 터치하면 이러한 다른 특성 모드가 억제됩니다. 그런 다음 이러한 다른 특성 모드의 조성 조화도 억제됩니다. 결과적으로 n이 3의 배수인^th n개의 특성 모드로부터의 조성 고조파는 상대적으로 더 두드러질 것입니다.^[1]

음악에서 하모닉은 현악기와 관악기에서 소리를 내는 방법으로 사용되며, 특히 높은 음을 연주하고 현악기에서는 독특한 음질이나 "음색"을 갖는 음을 얻습니다. 현악기에서 활 모양의 하모니카는 "유리 같은" 순수한 음색을 가지고 있습니다. 현악기에서 하모닉은 현을 울리면서 현의 정확한 지점을 터치(현을 완전히 누르지는 않음)하여 연주합니다(끌기, 절기 등).; 이것은 항상 현의 기본 주파수보다 높은 피치인 고조파가 소리를 낼 수 있게 합니다.

용어.

화성학은 "오버톤", "파탈" 또는 "상부파탈"이라고 불릴 수 있으며, 일부 음악 맥락에서는 "하모닉", "오버톤" 및 "파탈"이라는 용어가 상당히 상호 교환적으로 사용됩니다. 그러나 더 정확하게 말하면, "하모닉"이라는 용어는 (기본 주파수를 포함하여) 하모닉 계열의 모든 음정을 포함하는 반면, "오버톤"이라는 용어는 기본 위의 음정만을 포함합니다.

특성.

휘파람 소리를 내는 음색적인 특성은 자연적이고 인위적인 모든 화성과 견고하게 멈춘 간격을 구별합니다. 따라서 후자와 관련된 화성의 적용은 항상 신중하게 고려되어야 합니다.^{[citation needed]}

— 리처드 숄츠 c.(1888-1912)^[2]

대부분의 음향 기기는 많은 개별 부분을 포함하는 복잡한 음조를 방출하지만, 훈련되지 않은 인간의 귀는 일반적으로 이러한 부분을 별개의 현상으로 인식하지 않습니다. 오히려, 음표는 하나의 소리로 인식되며, 그 소리의 품질이나 음색은 개별 부분의 상대적인 강도의 결과입니다. 사람의 목소리나 현을 구부린 바이올린 줄과 같은 많은 음향 진동자들은 다소 주기적인 복잡한 음색을 만들어냅니다. 따라서 기본 주파수의 정수배와 거의 일치하는 부분들로 구성되며, 따라서 이상적인 고조파와 유사하며, 편의상 "하모닉 부분" 또는 간단히 "harmon학"이라고 불립니다(비록 부분을 고조파라고 부르는 것은 엄격하게 정확하지는 않지만, 첫 번째는 실제적인 존재이고 두 번째는 이론적인 존재입니다.

고조파 부분을 생성하는 진동자는 1차원 공명기처럼 행동하며, 종종 기타 줄이나 양쪽 끝이 열린 공기 기둥과 같이 길고 얇습니다(금속 현대 관현악 횡단 플루트와 마찬가지로). 트럼펫이나 클라리넷과 같이 공기 기둥이 한쪽 끝만 열려 있는 관악기들도 화성과 비슷한 부분들을 만들어냅니다. 그러나 그들은 적어도 이론적으로는 이상한 고조파와 일치하는 부분만 생산합니다. 실제 사용에서 실제 음향 악기는 단순화된 물리적 모델이 예측하는 것처럼 완벽하게 작동하지 않습니다. 예를 들어 금속 대신 비선형 탄성 목재로 만들거나 놋쇠나 강철 줄 대신 내장으로 끈을 묶은 악기는 그다지 정수가 없는 부분이 있는 경향이 있습니다.

주파수가 기본값의 정수배가 아닌 부분을 부조화 부분이라고 합니다. 일부 음향 악기들은 화성적인 부분과 비화음적인 부분의 혼합을 방출하지만, 피아노, 현의 불쑥 생겨난 피자토, 비브라폰, 마림바, 그리고 특정한 순수한 소리를 내는 종이나 차임벨과 같은 확실한 기본 음정을 갖는 귀에 여전히 영향을 줍니다. 고풍스러운 노래 그릇은 여러 개의 화성 파트나 다음향을 내는 것으로 알려져 있습니다. ^[3][4] 심벌즈, 드럼 헤드, 그리고 대부분의 타악기와 같은 다른 진동자들은 자연적으로 많은 비협조적인 부분들을 만들어내고, 어떤 특정한 음정을 암시하지 않기 때문에, 다른 악기들이 할 수 있는 것과 같은 방식으로 선율적으로 또는 조화롭게 사용될 수 없습니다.

세사레스(2004)^[5]를 기반으로 동적 음색은 의사 저스트 튜닝에서 각 부분의 주파수가 해당 음의 피치와 일치하도록 정렬되는 의사 고조파 부분의 개념을 도입하여 의사 저스트 튜닝의 음과 의사 고조파 음색의 자음을 극대화합니다.^[6][7][8][9]

파츠, 배음 및 고조파

오버톤은 컴파운드 톤의 최저 부분보다 높은 부분입니다. 부품의 상대적인 강도와 주파수 관계에 따라 악기의 음색이 결정됩니다. 오버톤과 파셜이라는 용어들의 유사성은 때때로 음악적 맥락에서 느슨하게 사용되는 것으로 이어지지만, 그것들은 다르게 계산되어 약간의 혼란을 야기합니다. (대부분의 음조 타악기와 같이) 화성적인 부분이 아닌 (대부분의 현과 관악과 같은) 고조파 계열과 거의 일치하는 악기 음색의 특별한 경우, (대부분의 음조 타악기와 같이) 부품을 "화음학"이라고 부르는 것도 편리하지만 엄밀하게 정확하지는 않습니다. 왜냐하면 화성학은 빠져도 같은 번호가 매겨지고, 파츠와 오버톤은 존재할 때만 계산되기 때문입니다. 이 차트는 세 가지 유형의 이름(부분, 오버톤 및 고조파)이 계산되는 방법을 보여줍니다(조화가 존재한다고 가정할 때).

빈도수.	주문 (n)	이름1	이름2	이름3	정상파 표현	종파 표현
1 × f = 0440 Hz	n = 1	1부	원초적인 어조	1차 고조파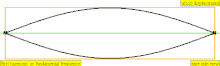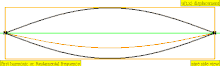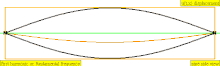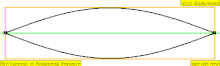
2 × f = 0880 Hz	n = 2	2부	오버톤 1번	2차 고조파
3 × f = 1320 Hz	n = 3	3부	두 번째 오버톤	3차 고조파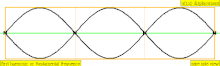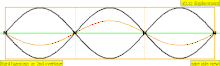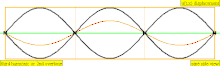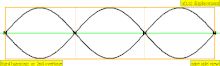
4 × f = 1760 Hz	n = 4	4부	세 번째 오버톤	4차 고조파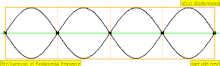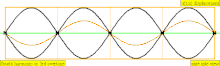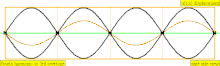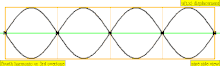

많은 악기에서 기본음이 존재하지 않고 상부 화성을 연주하는 것이 가능합니다. 단순한 경우(예: 녹음기)에는 음이 한 옥타브씩 올라가는 효과가 있지만, 더 복잡한 경우에는 다른 많은 음정 변화가 얻어집니다. 경우에 따라 음의 음색도 변경됩니다. 이것은 관악기에서 더 높은 음을 얻는 일반적인 방법의 일부이며, 이것을 오버블로우라고 합니다. 확장된 멀티포닉스 연주 기술은 또한 고조파를 생성합니다. 현악기에서는 현악기 연주자들이 하모닉스나 플라주렛이라고 부르는 매우 순수한 음을 내는 것이 가능한데, 음정이 높을 뿐만 아니라 섬뜩한 품질을 가지고 있습니다. 고조파를 사용하여 유니슨에 튜닝되지 않은 현의 튜닝을 유니슨으로 확인할 수 있습니다. 예를 들어, 첼로의 가장 높은 현의 반 아래에서 발견된 마디를 가볍게 손가락질하는 것은 마디를 가볍게 손가락질하는 것과 같은 음정을 만들어냅니다. 두 번째로 높은 줄 아래로 가는 길의 1/3. 인간의 목소리는 화성학을 사용하는 Overtone sing을 참조하세요.

전자적으로 생성된 주기음(예: 사각파 또는 기타 비시누이드파)이 기본 주파수의 정수배인 "하모닉스"를 갖는 것은 사실이지만, 실용적인 악기들이 모두 이러한 특성을 갖는 것은 아닙니다. 예를 들어, 피아노 음의 더 높은 "하모닉스"는 진정한 하모닉스가 아니라 "오버톤"이며 매우 날카로울 수 있습니다. 즉, 순수한 하모닉스 계열에 의해 주어지는 것보다 더 높은 주파수일 수 있습니다. 이것은 특히 현악기, 금관악기 또는 목관악기 이외의 악기에 해당됩니다. 이러한 "기타" 악기들의 예로는 실로폰, 드럼, 종, 차임벨 등이 있습니다. 모든 현음 주파수가 기본 주파수와 단순한 정수비를 이루는 것은 아닙니다. (기본 주파수는 어떤 단일 주기 현상에서 진동 모음의 가장 긴 시간의 역수입니다.)^[10]

현악기에서

하모닉스는 활과 접촉하는 지점을 달리하여 [현악기](1) 단독으로 제작하거나, (2) 마디에서 현을 살짝 눌러 제작하거나, 부분 부분의 분할(${\displaystyle \frac{\text{12}}{\mathrm{}}}$ ${\$ ${\displaystyle \frac{\text{13}}{\mathrm{}}}$ ${\$ ${\displaystyle \frac{\text{14}}{\mathrm{}}}$ ${\$}{$4$ 등). (1) 첫 번째 경우, 기본음이 나오는 일반적인 장소에서 다리 쪽으로 활을 전진시키면 전체 음계의 고조파가 오래되고 공명도가 높은 악기로 연속적으로 생성될 수 있습니다. 이 수단을 사용하면 'sul ponticello'라는 효과가 발생합니다. (2) 열린 현에 손가락이 약간 눌려서 하모닉스를 만드는 것이 더 유용합니다. 열려 있는 현의 다양한 마디를 살짝 눌러 생성하면 '자연 조화학'이라고 합니다. 바이올린 연주자들은 줄의 굵기에 비례하여 줄이 길어질수록 더 많은 상위 화성을 산출할 수 있다는 것을 잘 알고 있습니다.

— Grove's Dictionary of Music and Musicians (1879)^[11]

다음 표는 현악기에서 현을 부드럽게 만지면 진동 시 조화 모드로 전환되는 정지점을 보여줍니다. 현악 화성학(플라자 톤)은 오케스트라에서 사용하고 들을 때 특별한 색 또는 음색(팀브레)으로서 높은 효과를 발휘할 수 있는 "플루트라이크한, 은질"을 가진 것으로 설명됩니다.^[12] 더블 베이스를 제외한 어떤 현악기에서도 5부 이상의 자연스러운 화성을 접하는 것은 매우 드문 일인데, 이는 현의 길이가 훨씬 길기 때문입니다.^[12]

고조파	중지 노트	음이 울렸습니다. (relative에서) 오픈스트링)	오디오 주파수(Hz)	위의 센트 기본(옥타브 단위 offset)	오디오 (옥타브 이동)
1	기본적인, 완전한 일치	P1	600	0.0	놀고ⓘ
2	첫 퍼펙트 옥타브	P8	1,200	0.0	놀고ⓘ
3	완벽한 5분의 1	P8 + P5	1,800	702.0	놀고ⓘ
4	2배의 완벽한 옥타브	2·P8	2,400	0.0	놀고ⓘ
5	3번째로 중요한 것은 3분의 1의	2·P8+M3	3,000	386.3	놀고ⓘ
6	완벽한 5분의 1	2·P8+P5	3,600	702.0	놀고ⓘ
7	화성 7번, 9분의 7분의 1 ('잃어버린 화음')	2·P8+m7↓	4,200	968.8	놀고ⓘ
8	3분의 1옥타브	3·P8	4,800	0.0	놀고ⓘ
9	피타고라스어 제2의 장조	3·P8+M2	5,400	203.9	놀고ⓘ
10	겨우 3분의 1의	3·P8+M3	6,000	386.3	놀고ⓘ
11	더 적은 운데시멀 트리톤, 반진법 augmented 4위	3·P8+a4	6,600	551.3	놀고ⓘ
12	완벽한 5분의 1	3·P8+P5	7,200	702.0	놀고ⓘ
13	삼십진법 중립 6위	3·P8+n6↓	7,800	840.5	놀고ⓘ
14	화성 7번, 9분의 7분의 1 ('잃어버린 화음')	3·P8+m7	8,400	968.8	놀고ⓘ
15	그저. 제7장조	3·P8+M7	9,000	1,088.3	놀고ⓘ
16	네 번째 완벽한 옥타브	4·P8	9,600	0.0	놀고ⓘ
17	정십진반음	4·P8+m2	10,200	105.0	놀고ⓘ
18	피타고라스어 제2의 장조	4·P8+M2	10,800	203.9	놀고ⓘ
19	나노 소수 3분의 1	4·P8+m3	11,400	297.5	놀고ⓘ
20	겨우 3분의 1의	4·P8+M3	12,000	386.3	놀고ⓘ

인공하모닉스

때때로 악보는 이미 멈춘 현 위에서 오버톤을 연주함으로써 생성되는 인공 고조파를 요구합니다. 연주 기법으로, 그것은 핑거보드에 두 손가락을 사용하여 수행되며, 첫 번째는 현을 원하는 기본으로 단축하고 두 번째는 적절한 고조파에 해당하는 노드를 만집니다.

다른 정보

고조파는 성조 시스템에서 사용되거나 또는 단지 억양 시스템의 기초로 간주될 수 있습니다. 작곡가 아놀드 드레블랫은 그의 독특한 활 기술을 현을 치는 것과 굽히는 것 사이의 중간에서 약간 변경함으로써 그의 변형된 더블 베이스의 단일 현에 다른 하모니를 끌어낼 수 있습니다. 작곡가 로렌스 볼(Lawrence Ball)은 하모닉스(harmonics)를 사용하여 음악을 전자적으로 생성합니다.

참고 항목

• 아리스톡세누스
• 전자 튜너
• 포름트
• 푸리에 급수
• 기타하모닉
• 고조파 분석
• 하모닉스(전력)
• 고조파 생성
• 고조파 발진기
• 하모니
• 순음
• 피타고라스 음정
• 하모닉스의 척도
• 구면 하모닉스
• 늘린옥타브
• 서브하모닉
• 젠하모닉 음악

참고문헌

외부 링크

• 물리학에 관한 파인만 강의: 하모닉스
• 기본 주파수에서 나오는 고조파, 파츠 및 오버톤
• Chisholm, Hugh, ed. (1911). "Harmonic" . Encyclopædia Britannica (11th ed.). Cambridge University Press.
• 하모닉스
• 피아노로 하모니카 듣고 보기