빠른 역제곱근

조명 및 반사 계산(1인칭 슈터OpenArena에 표시됨)은 발생과 반사의 각도를 계산하기 위해 빠른 역제곱근 코드를 사용한다.

Fast inverse square root, sometimes referred to as Fast InvSqrt() or by the hexadecimal constant 0x5F3759DF, is an algorithm that estimates ${\displaystyle {\frac {1}{\sqrt {x}}}}$, the reciprocal (or multiplicative inverse) of the square root of a 32-bit floating-point number ${\displaystyle x}$ in IEEE 754 floating-point f오마트. 이 조작은 벡터를 정상화하는 디지털 신호 처리, 즉 길이 1까지 스케일링하는 데 사용된다.예를 들어, 컴퓨터 그래픽 프로그램은 조명 및 음영에 대한 입사각과 반사를 계산하기 위해 역제곱근을 사용한다.이 알고리즘은 3D 그래픽을 많이 사용한 1인칭 슈터 비디오 게임인 '지진 III 아레나'의 소스 코드에서 1999년에 구현된 것으로 가장 잘 알려져 있다.이 알고리즘은 2002년 또는 2003년에야 유스넷과 같은 공개 포럼에 등장하기 시작했다.^{[note 1]}제곱근의 계산은 대개 많은 분할 연산에 의존하는데, 부동 소수점 숫자의 경우 계산적으로 비용이 많이 든다.빠른 역제곱은 단 하나의 분할 단계만으로 좋은 근사치를 생성했다.쯔진 3보다 앞서 나온 다른 비디오 게임들은 쯔진 구현이 가장 잘 알려진 사례로 남아있지만 유사한 알고리즘을 사용하는 것이 발견되었다.

알고리즘은 32비트 부동 소수점 숫자를 입력으로 받아들이고 나중에 사용하기 위해 반감된 값을 저장한다.그런 다음 부동 소수점 숫자를 나타내는 비트를 32비트 정수로 처리하여 논리 이동 우측 1비트를 수행하고 그 결과를 0x5F3759DF(십진수 표기법: 1,597,463,007)에서 빼서 ${\displaystyle$ {\$sqrt{2^{127}}}}}}$의 근사치를 나타내는 부동 소수점 표현이다$.$^[2]이렇게 하면 입력의 역제곱근에 대한 첫 번째 근사치가 나온다.비트를 다시 부동 소수점 숫자로 처리하면 뉴턴의 방법을 한 번 반복하여 더 정확한 근사치를 산출한다.

이 알고리즘은 원래 존 카맥에 기인했지만 조사 결과 컴퓨터 그래픽의 하드웨어와 소프트웨어 측면 모두에서 코드가 더 깊이 뿌리내린 것으로 나타났다.조정과 변경은 실리콘 그래픽스와 3dfx Interactive를 모두 통과했으며, 원래의 상수는 1980년대 후반에 그레고리 월시와 Cleve Moler의 협업으로 도출되었다.^[3]월시와 몰러는 윌리엄 카한과 K.C.의 미발표 논문에서 그들의 버전을 개작했다.Ng는 1986년 5월에 유통되었다.

후속 하드웨어 향상, 특히 x86SSE 지침서rsqrtss이 방법은 역사적으로나^[5] 저비용 임베디드 시스템과 같은 좀 더 제한된 기계에 대해 흥미로운 예로 남아있지만,^[4] 일반적으로 범용 컴퓨팅에는 적용되지 않는다.그러나, 더 많은 임베디드 시스템 제조업체들은 삼각측정학 및 CODIC와 같은 다른 연산 가속기를 포함하여 그러한 알고리즘의 필요성을 배제하고 있다.

동기

표면 표준은 조명 및 음영 계산에 광범위하게 사용되며 벡터에 대한 규범 계산이 필요하다.표면에서 정상적인 벡터 필드가 여기에 표시된다.

일반 $C{\displaystyle }$ ${\displaystyle C}$을(를) 사용하여$$ 입사각에서 반사각을 찾는 2차원 예. 이 경우 곡선 거울에서 반사되는 빛에 대한 예.빠른 역제곱근은 이 계산을 3차원 공간으로 일반화하는 데 사용된다.

부동소수점수의 역제곱근은 정규화된 벡터 계산에 사용된다.^[6]프로그램은 발생과 반사의 각도를 결정하기 위해 정규화된 벡터를 사용할 수 있다. 3D 그래픽 프로그램은 조명을 시뮬레이션하기 위해 매초 수백만 개의 이러한 계산을 수행해야 한다.1990년대 초 코드가 개발되었을 때, 대부분의 부동 소수점 처리 능력은 정수 처리 속도에 뒤처졌다.^[7]이는 변환과 조명을 다루는 전문 하드웨어가 등장하기 전 3D 그래픽 프로그램에게는 골칫거리였다.

벡터 길이는 그 유클리드 규범인 벡터 성분의 제곱합 제곱근을 계산하여 결정한다.벡터의 각 성분이 그 길이로 나누어질 때, 새로운 벡터는 같은 방향을 가리키는 단위 벡터가 될 것이다.3D 그래픽 프로그램에서 모든 벡터는 3차원 공간에 있으므로 $v{\displaystyle \mathit{}}$ ${\$은(는) 벡터$({\displaystyle {v\mathrm{}}_{}}$ 1,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {3\mathrm{}}_{}}$) ${\displaystyle (v_{1}, v_{2}, v_{3})$이 될 것이다$.$

${\displaystyle \{\symbol{v}\ ={\sqrt {v_{1}^{2}+v_{2}}^{2}+v_{3}^{2}}}}$

벡터의 유클리드 규범이야

${\displaystyle {\jamsymbol {\hat {v}={\frac {\b}{\좌측\{\bmbcol {v}\오른쪽\}}}}}}$

표준화된(단위) 벡터로서, $v{\displaystyle {}_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ ${\displaystyle {2\mathrm{}}_{}^{}}$+ v ${\displaystyle {2\mathrm{}}_{}^{}}$ + ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$+ v 3 ${\displaystyle {\mathrm{}}_{}^{}}$ + v ${\displaystyle {}_{}^{}}$ 2 ${\$2} + v_{$2$$}$를 나타내기 위해$$ $‖$ ${\displaystyle v\mathit{}}$ ${\displaystyle \Vert {}^{}}$ ${\displaystyle {v\mathrm{}}^{}}$ $\$2 {\displaystyle v_{$1}+v_{$2}{2}를 사용한다.$}^{2}+v_{3$$}^{2}}$.

${\displaystyle {\jamsymbol {\hat{v}}={\frac {\b}{\sqrt {\\\\bmbol {v}\right\{2}}:}}}$

거리 성분의 역제곱근과 단위 벡터를 연관시킨다.역제곱근은 $v{\displaystyle \widehat{\mathit{}}}$ ${\$과(와) 동일하므로 계산에$$ 사용할 수 있다.

${\displaystyle {\jamsymbol {\hat {v}={\jamsymbol {v}\}\\frac {1}{1}{\sqrt {\\\\\chmbol {v}\right\{2}}:}}}$

여기서 분율항은${\displaystyle }$term v ‖${\displaystyle {}^{2\mathrm{}}}$ ${\$의 역제곱근이다$.$

그 당시 부동 소수점 분할은 일반적으로 곱셈에 비해 비용이 많이 들었고, 빠른 역 제곱근 알고리즘은 분할 단계를 우회하여 성능 우위를 제공했다.1인칭 슈터 비디오 게임인 쯔진Ⅲ 아레나는 그래픽 계산을 가속화하기 위해 빠른 역제곱근 알고리즘을 사용했지만, 이후 이 알고리즘은 필드 프로그래밍 가능한 게이트 어레이(FPGA)를 이용한 일부 전용 하드웨어 정점 쉐이더에서 구현되었다.^[8]

코드 개요

다음 코드는 C 전처리기 지침이 벗겨진 Quin III Arena에서 신속하게 역제곱근을 구현하는 것이지만 정확한 원본 주석 텍스트를 포함한다.^[9]

둥둥 뜨다 Q_rsqrt( 둥둥 뜨다 번호를 붙이다 ) {  장기의 i;  둥둥 뜨다 x2, y;  경시하다 둥둥 뜨다 반쪽짜리 = 1.5층;   x2 = 번호를 붙이다 * 0.5F;  y  = 번호를 붙이다;  i  = * ( 장기의 * ) &y;                       // 사악한 부동소수 비트 레벨 해킹  i  = 0x5f3759df - ( i >> 1 );               // 대체 뭐야?   y  = * ( 둥둥 뜨다 * ) &i;  y  = y * ( 반쪽짜리 - ( x2 * y * y ) );   // 1차 반복 // y = y * ( 3 1/2초 - ( x2 * y * y ); // 2차 반복, 제거 가능   돌아오다 y; } 

당시 역제곱근을 계산하는 일반적인 방법은 1 ${\displaystyle \frac{\sqrt{x}}{}}$ ${\$에 대한 근사치를 계산한$$다음 실제 결과의 허용 오차 범위 내에 도달할 때까지 다른 방법을 통해 근사치를 수정하는 것이었다.1990년대 초의 일반적인 소프트웨어 방법은 조회표에서 근사치를 도출했다.^[10]빠른 역제곱근의 핵심은 부동 소수점 구조를 활용해 근사치를 직접 계산해 테이블 룩업보다 빠르게 증명하는 것이었다.알고리즘은 다른 방법으로 제곱근을 계산하고 부동 소수점 분할을 통해 역수를 계산하는 것보다 약 4배 더 빨랐다.^[11]알고리즘은 IEEE 754-1985 32비트 부동 소수점 사양을 염두에 두고 설계되었지만, 크리스 로몬트의 조사 결과 다른 부동 소수점 사양의 구현이 가능한 것으로 나타났다.^[12]

빠른 역제곱근법에서 제공하는 속도의 장점은 32비트 부동소수 단어를^{[note 2]} 정수로 처리한 다음 "마법" 상수에서 빼는 데서 비롯되었다.0x5F3759DF.^{[7][13][14][15]}이 정수 뺄셈과 비트 시프트는, 부동 소수점 숫자로 다시 정의할 때, 숫자의 역 제곱근에 대한 대략적인 근사치를 나타내는 비트 패턴을 낳는다.뉴턴의 방법 중 한 번을 반복하면 어느 정도 정확성을 얻을 수 있고, 코드는 완성된다.알고리즘은 뉴턴의 방법에 대한 고유한 첫 번째 근사치를 사용하여 합리적으로 정확한 결과를 생성하지만 SSE 명령을 사용하는 것보다 훨씬 느리고 정확도가 낮다.rsqrtss또한 1999년에 출시된 x86 프로세서에 탑재되었다.^[4][16]

작업 예제

예를 들어 $숫자{\displaystyle }$x = 0.${\displaystyle 15625}$ ${\displaystyle x=0.15625}$을(를) 사용하여 $1{\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \frac{\sqrt{x}}{}}$≈${\displaystyle 2.52982}$ ${\displaystyle {\frac {1}{\sqrt {x}}\ 약 2.52982}$을(를) 계산할 수 있다$$$.$알고리즘의 첫 번째 단계는 다음과 같다.

0011_1110_0010_0000_0000_0000_0000_0000  Bit pattern of both x and i 0001_1111_0001_0000_0000_0000_0000_0000  Shift right one position: (i >> 1) 0101_1111_0011_0111_0101_1001_1101_1111  The magic number 0x5F3759DF 0100_0000_0010_0111_0101_1001_1101_1111 0x5F3759DF - (i > 1)

IEEE 32비트 표현으로 해석:

0_01111100_01000000000000000000000  1.25 × 2−3 0_00111110_00100000000000000000000  1.125 × 2−65 0_10111110_01101110101100111011111  1.432430...× 263 0_10000000_01001110101100111011111  1.307430...× 21

이 마지막 비트 패턴을 부동 소수점 숫자로 재해석하면 약 3.4%의 오차를 갖는 ${\displaystyle \mathrm{근사}}$y = 2.$[\displaystyle$ y$=2.61486}$이$($가) 제공된다.뉴턴의 방법을 한 번 반복한 후에 최종 결과는 $y{\displaystyle }$=$[\displaystyle y=2.52549}$이며$,$ 오차 범위는 0.17%에 불과하다.

정의되지 않은 동작 방지

C 표준에 따르면, 부동소수점 값을 포인터를 제거하여 정수로 재해석하면 예기치 않은 동작(정의되지 않은 동작)을 유발할 수 있는 것으로 간주된다.또 다른 방법은 32비트 부호 없는 정수 멤버를 추가로 포함하는 익명 조합에 부동소수 값을 배치하고, 그 정수에 대한 액세스는 부동소수 값 내용에 대한 비트 레벨 뷰를 제공하는 것이다.그러나 유니온을 통한 펀칭은 C++에서도 정의되지 않은 행동이다.

#include <stdint.h>// uint32_t   둥둥 뜨다 Q_rsqrt(둥둥 뜨다 번호를 붙이다) {  결합하다 {   둥둥 뜨다    f;   uint32_t i;  } 수녀원으로 모이다 = { .f = 번호를 붙이다 };  수녀원으로 모이다.i  = 0x5f3759df - (수녀원으로 모이다.i >> 1);  수녀원으로 모이다.f *= 1.5층 - (번호를 붙이다 * 0.5F * 수녀원으로 모이다.f * 수녀원으로 모이다.f);  돌아오다 수녀원으로 모이다.f; } 

C++에서 이 기능의 깁스를 구현하는 일반적인 방법은 C++20을 통해서이다.std::bit_cast이것은 또한 이 기능이 다음에서 작동할 수 있도록 한다.constexpr컨텍스트:

#include <비트> #include <<limits>> #include <씨스트딘트>  경구적 둥둥 뜨다 Q_rsqrt(둥둥 뜨다 번호를 붙이다) 예외로 {  static_properties(찌꺼기::numeric_message<둥둥 뜨다>::is_iec559); // (IEEE 754에서만 활성화)   둥둥 뜨다 경시하다 y = 찌꺼기::비트_캐스트<둥둥 뜨다>(         0x5f3759df - (찌꺼기::비트_캐스트<찌꺼기::uint32_t>(번호를 붙이다) >> 1));  돌아오다 y * (1.5f - (번호를 붙이다 * 0.5f * y * y)); } 

알고리즘.

알고리즘은 다음 단계를 수행하여$$ $1{\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \frac{\sqrt{x}}{}}$ ${\$을(를) 계산한다.

1. 이진 로그 ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle {2\mathrm{}}_{}(x}$) ${\displaystyle \log _{2}(x)}$의 근사치를 계산하는 방법으로 $인수$를 정수에$$별칭 지정
2. 이 근사치를 사용하여 ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$⁡(${\displaystyle \frac{\sqrt{1}}{}}$x${\displaystyle }$) =${\displaystyle }$- ${\displaystyle 1\frac{\mathrm{}}{}}$ 2 ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle {2\mathrm{}}_{}(x}$) ${\displaystyle \log _{2$}\$log$ _{2$}\$left$({\frac {1}{sqrt{x}}\오른쪽)=-{\frac {1}{1$}2$}}\log _{2}(x)$의 근사치를 계산하십시오.
3. base-2 지수 근사치를 계산하는 방법으로 플로트에 대한 별칭 되돌리기
4. 뉴턴의 방법의 단일 반복을 사용하여 근사치를 정제한다.

부동 소수점 표현

이 알고리즘은 단일 정밀 부동 소수점 숫자의 비트 레벨 표현에 크게 의존하므로, 이 표현에 대한 간략한 개요를 여기에 제공한다.0이 아닌 실수 $x{\displaystyle }$ ${\displaystyle x}$을(를) 하나의 정밀 플로트로 인코딩하려면 첫 번째 단계는 ${\displaystyle normalized{}^{}{}^{}}$x ${\displaystyle {″}^{}}$ ${\$ "x$"를$정규화된 이진수로 쓰는 것이다.^[17]

${\displaystyle {\m_{x}=\pm 1.b_{1}b_{2}b_{3}\ldots \^2^{e_{x}\&=pm 2^{x}}{x}}}}{x}}}\pm2^{x}}}{x}}}}\ended}}}}}}}}}}}}}}}}}}}}}}}?$

where the exponent ${\displaystyle e_{x}}$ is an integer, ${\displaystyle m_{x}\in [0,1)}$, and ${\displaystyle 1.b_{1}b_{2}b_{3}\ldots }$ is the binary representation of the "significand" ${\displaystyle (1+m_{x})}$. Since the single bit before the point 의의는 항상 1이며, 저장될 필요가 없다.이 양식에서 세 개의 부호 없는 정수를 계산한다.^[18]

• ${\displaystyle S_{}}$ ${\displaystyle x_{}}$ ${\$$x{\displaystyle }$ ${\displaystyle x}$이(가) $양수$이고 1$${\$displaystyle 1$} 음수$$ 또는 0(1비트)이면$$ "신호 비트"는 $0{\displaystyle \mathrm{}}$ ${\displaystyle$ 0$}$입니다.
• ${\displaystyle E_{}}$ ${\displaystyle x_{}}$= ${\displaystyle e}$ ${\displaystyle {}_{}}$+ B ${\displaystyle E_{x}=e_{x}+B}$는 "편향된 지수"이며, 여기서 $B{\displaystyle }$= ${\displaystyle 127}$ ${\displaystyle B=127}$은 "우수 바이어스"(8비트)이다.^{[note 3]}
• ${\displaystyle M_{}}$ ${\displaystyle x_{}}$= ${\displaystyle m}$ ${\displaystyle x_{}}$ ${\displaystyle {}_{}}$ L ${\displaystyle M_{x}=m_{x}\time L$ 여기서 $L{\displaystyle }$= 2 ${\displaystyle {23}^{}}$ ${\$^{[note 4]}23비트)

그런 다음 이 들판은 왼쪽에서 오른쪽으로 32비트 컨테이너에 포장된다.^[19]

예를 들어 $x{\displaystyle }$=${\displaystyle 0.15625}$= ${\displaystyle {.00101}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$$displaystyle$ $x=0.15625=0.$$00101_{$$2$ x $산출량$ 정규화$:$

${\displaystyle x=+2^{-3}(1+0.25)}$

따라서 세 개의 부호 없는 정수 필드는 다음과 같다.

• $[\displaystyle S=0}$
• ${\displaystyle E=-3+127=124=0111\ 1100_{2}}$
• $[\displaystyle M=0.25\time 2^{23}=2\ 097\ 152=0010\ 0000\ 0000\ 0000\ 0000\ 0000_{2]}}$

이 필드는 아래 그림과 같이 포장되어 있다.

대략적인 로그로 정수에 앨리어싱

If ${\displaystyle {\frac {1}{\sqrt {x}}}}$ were to be calculated without a computer or a calculator, a table of logarithms would be useful, together with the identity ${\displaystyle \log _{b}\left({\frac {1}{\sqrt {x}}}\right)=\log _$${b}\왼쪽(x^{-{\frac {1}{1$}:{2$}}\\오른쪽)=-{{\frac {1}{2}}\log _{b}(x$ 모든 $base{\displaystyle }$ b ${\displaystyle b}$에 유효하다$.$빠른 역제곱근은 이 정체성에 기초하며, float32를 정수에 앨리어싱하면 그 로그의 대략적인 근사치를 얻을 수 있다는 사실에 기초한다.방법은 다음과 같다.

$x{\displaystyle }$ ${\displaystyle x}$이(가) 양의 정규 숫자인 경우:

${\displaystyle x=2^{e_{x}}(1+m_{x})}$

그때

${\displaystyle \log _{2}(x)=e_{x}+\log_{2}(1+m_{x}})$

그리고 $m{\displaystyle {}_{}}$ ${\displaystyle x_{}}$ ${\displaystyle {}_{}}$[ 0${\displaystyle }$, ${\displaystyle 1}$) ${\displaystyle m_{x}\in [0,1)]$에서 우측의 로그는 다음과^[20] 같이 근사할 수 있다$.$

${\displaystyle \log _{2}(1+m_{x})\cHB m_{x}+\ma }$

여기서 $\sigma {\displaystyle }$ ${\displaystyle \sigma}$은 근사치를 조정하기 위해 사용되는 자유 매개 변수다.For example, ${\displaystyle \sigma =0}$ yields exact results at both ends of the interval, while ${\displaystyle \sigma ={\frac {1}{2}}-{\frac {1+\ln(\ln(2))}{2\ln(2)}}\approx 0.0430357}$ yields the optimal approximation (the best in the sense of the uniform 오차의 규범).그러나 이 값은 후속 단계를 고려하지 않기 때문에 알고리즘에 의해 사용되지 않는다.

확장 및 이동 로그(회색)와 비교하여 부동 소수점 번호(파란색)로 앨리어싱된 정수.

따라서 근사치가 있다.

${\displaystyle \log _{2}(x)\trawth e_{x}+m_{x}+\ma .}$

$x{\displaystyle }$ ${\displaystyle x}$의 부동 소수점 비트 패턴을 정수 $I{\displaystyle {}_{}}$ ${\displaystyle x_{}}$ ${\$ 수익률로$$$$^{[note 5]} 해석

${\displaystyle {\reasoned}I_{x}&=E_{x}L+M_{x}\\&=L(e_{x}+B+m_{x})\\&=L(e_{x}+m_{x}+\sigma +B-\sigma )\\&\approx L\log _{2}(x)+L(B-\sigma ).\end{정렬}}}$

${\displaystyle {그런}_{}}$ 다음 $I{\displaystyle {}_{}}$ x ${\$은(는) 오른쪽 그림에서와 같이 ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ (${\displaystyle x}$) ${\displaystyle \log _{2}(x$의 크기 조정 및 이동된 조각 선형의 근사치로 나타난다$$.즉, ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {}_{}}$( ${\displaystyle x}$) ${\displaystyle \log _{2}(x)}$의 근사치를

${\displaystyle \log _{2}(x)\약간 {\frac {I_{x}}{L}-(B-\sigma).}$

결과의 첫 번째 근사치

$y{\displaystyle }$= ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{\sqrt{x}}{}}$ ${\$의 계산은 ID를 기반으로 한다$$.

${\displaystyle \log _{2}(y)=-{\tfrac {1}{1}:{2}}\log _{2}(x)}$

$x{\displaystyle }$ ${\displaystyle x}$ 및$$ $y{\displaystyle }$ ${\displaystyle y}$ 모두에 적용되는 위의 로그의 근사치를 사용하여 위의 방정식은 다음을 제공한다$.$

${\displaystyle {\frac {I_{y}}{L}-{L}-(B-\sigma )\ 약 -{{\frac {1}{1}2}}\왼쪽({\frac {I_{x}}}{L}-(B-\sigma )\오른쪽)}}$

따라서 $I{\displaystyle {}_{}}$ ${\displaystyle y_{}}$ ${\$의 근사치는 다음과$$ 같다.

${\displaystyle I_{y}\약간 {\tfrac {3}{2}}L(B-\sigma )-{\tfrac {1}{2}}:I_{x}}$

암호에 다음과 같이 쓰여 있다.

i  = 0x5f3759df - ( i >> 1 ); 

위의 첫 번째 용어는 마법의 숫자다.

${\displaystyle {\tfrac {3}{2}}L(B-\sigma )={\matht {0x5F3759DF}}$

여기서 $\sigma {\displaystyle 04}$ 0.${\displaystyle 0450466}${\$displaystyle \sigma \ 약$0$.0450466}$을(를) 유추할 수 있다$.$두 번째 학기, $1{\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \frac{2}{}}$ ${\displaystyle I{}_{}}$ ${\displaystyle x_{}}$ ${\$$I_{x$는 $I{\displaystyle {}_{}}$ x ${\$의 비트를 오른쪽으로 한 위치 이동시켜$$ 계산한다.^[21]

뉴턴의 방법

뉴턴의 뿌리 찾기 방법의 0, 1, 2, 3, 4회 반복을 수행하는 직접 계산과 빠른 역제곱근 사이의 상대 오차.4회 반복을 수행한 후에는 이중 정밀도를 채택하고 두 개의 이중 정밀도 수 사이의 가장 작은 차이점에 도달한다는 점에 유의하십시오.

$y{\displaystyle }$ ${\displaystyle y}$을(를) 역제곱근으로 하여$$ $f{\displaystyle (}$ y${\displaystyle }$) = ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{{y\mathrm{}}^{}}{}}$ ${\displaystyle \frac{{}^{}}{}}$- ${\displaystyle x}$= ${\displaystyle 0}$ ${\displaystyle f(y)={\frac {1}{y^{2}}-x=0}$.초기 단계에서 산출한 근사치는 함수의 0을 찾는 방법인 뿌리 찾기 방법을 사용하여 정제할 수 있다.The algorithm uses Newton's method: if there is an approximation, ${\displaystyle y_{n}}$ for ${\displaystyle y}$, then a better approximation ${\displaystyle y_{n+1}}$ can be calculated by taking ${\displaystyle y_{n}-{\frac {f(y_{n})}{f'(y_{n})}}}$, w${\displaystyle {여기}_{}}$서 $f{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$(${\displaystyle {}_{}}$y$$) {\$displaystyle f'($${\displaystyle \mathrm{y\_}}$${n$}})는$$ $y{\displaystyle {}_{}}$ {\$displaystyle$y_{$n}$에서 $f{\displaystyle }$( y${\displaystyle }$) ${\displaystyle f(y)}$의 파생어다$.$^[22] 위의 $f{\displaystyle }$( ${\displaystyle y}$) ${\displaystystyle f(y)}$에 대해$,$

${\displaystyle y_{n+1}={\frac {y_{n}\왼쪽(3-xy_{n}^{2}\오른쪽){2}}:}$

여기서 ${\displaystyle f(}$ y${\displaystyle }$)${\displaystyle }$= ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle y}$ 2${\displaystyle \frac{{}^{}}{}}$- x ${\displaystyle f(y)={\frac {1}{2}}-x}$ 및$$ $f{\displaystyle {}^{}(}$ ${\displaystyle y}$)${\displaystyle }$=${\displaystyle }$- ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \frac{{3\mathrm{}}^{}}{}}$ ${\$ f$'(y)=-{\frac {2}{y^{3$

$y{\displaystyle }$ ${\displaystyle y}$을(를) 부동 소수점 숫자로$$ 처리하고,y = y*(threehalfs - x/2*y*y);와 같다

${\displaystyle y_{n+1}=y_{n}\frac {3}{3}-{2}}-{x}{n}^{2}\오른쪽)={\frac {y_{n}\n}\frac {n}\(3-xy_{n}^{2}\rig){2}.}$

이 단계를 반복함으로써 함수 출력$($${\displaystyle {yn}_{}}$+ ${\displaystyle 1_{}}$ ${\$+1$})$을 다음 반복의 입력으로 사용하여 y ${\displaystyle y}$이(가)^[23] 역제곱근에 수렴하게 된다.쯔진 III 엔진의 목적상, 단 하나의 반복만 사용되었다.두 번째 반복은 코드에 남아 있었지만 코멘트를 받았다.^[15]

정확도

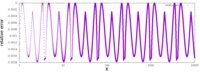
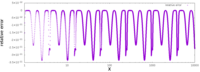
위에서 언급한 바와 같이 근사치는 놀라울 정도로 정확하다.오른쪽의 단일 그래프는 0.01에서 시작하는 입력에 대해 함수의 오차(즉, 뉴턴의 방법의 한 번 반복을 실행하여 개선된 후의 근사치의 오차)를 표시하는데, 여기서 표준 라이브러리는 결과적으로 10.0을 주는 반면, InvSqrt()는 9.982522를 주어 차이를 0.0017478 또는 참 값의 0.175%로 만든다.10. 절대 오차는 그때부터 감소할 뿐 상대 오차는 모든 규모의 순서에 걸쳐 동일한 범위 내에 머무른다.

역사

퀘이크 3세의 소스 코드는 퀘이크콘 2005년까지는 공개되지 않았으나, 빠르면 2002년 또는 2003년경 우에스넷 등 포럼에 빠른 역제곱 루트 코드의 복사본이 등장했다.^[7]초기의 추측들은 존 카맥이 이 코드의 유력한 저자로 지목했지만, 원작자들은 3D 컴퓨터 그래픽의 역사에서 훨씬 더 오래 전 것으로 증명되었다.라이스 소메펠트는 MATLAB의 창시자인 클레브 몰러와 협의해 그렉 월시가 애프터 컴퓨터(Active Computer)에서 만든 알고리즘이라고 결론지었다.^[3]클레브 몰러는 1986년경 버클리대학에서 윌리엄 카한과 K.C. Ng가 쓴 암호로부터 이 속임수에 대해 배웠다.^[24]

Jim Blinn은 IEEE 컴퓨터 그래픽스 및 어플리케이션용 1997년 칼럼에서 역제곱근의 간단한 근사치를 시연하기도 했다.^[25][26]다른 현대 3d 비디오 게임의 역 엔지니어링은 퀘이크 3 아레나가 출판되기 2년 전인 1997년 Activision의 주간지 76에서 알고리즘의 변형을 밝혀냈다.^[27]

후속 개선

매직넘버

매직넘버의 정확한 값이 어떻게 결정되었는지는 정확히 알려지지 않았다.크리스 로몬트는 범위보다 매직 번호$$ R ${\displaystyle$ R$}$을(를) 선택하여 근사 오차를 최소화하는 기능을 개발했다.그는 먼저 선형 근사 단계의 최적 상수를 0x5F3759DF에 가까운 0x5F37642F로 계산했지만, 이 새로운 상수는 뉴턴의 방법을 한 번 반복한 후 정확도가 약간 떨어졌다.^[28]이어 로몬트는 뉴턴이 1, 2회 반복해도 일정한 최적 상태를 찾아 모든 반복 단계에서 원본보다 정확한 0x5F375A86을 찾아냈다.^[28]그는 원래의 상수의 정확한 값이 파생이나 시행착오를 통해 선택되었는지를 물어봄으로써 결론을 내렸다.^[29]로몬트는 64비트 IEEE754 크기 타입 더블의 매직넘버는 0x5FE6EC85E7DE30DA이지만, 나중에 매튜 로버트슨에 의해 정확히 0x5FE6로 나타났다고 말했다.EB50C7B537A9.^[30]

Jan Kadlec는 또한 단일 뉴턴의 방법 반복에서 상수를 조정하여 상대 오차를 2.7의 추가 인수로 감소시켰다.^[31]

 수녀원으로 모이다.i = 0x5F1FFFF9 - ( 수녀원으로 모이다.i >> 1 );  수녀원으로 모이다.f *= 0.703952253f * ( 2.38924456f - x * 수녀원으로 모이다.f * 수녀원으로 모이다.f );  돌아오다 수녀원으로 모이다.f; 

단정밀 부동 소수점 숫자에 대해 매직 넘버를 결정하기 위한 완전한 수학적 분석이 현재 이용 가능하다.^[32][33]

제로 소견

속도와 정확성 면에서 뉴턴의 방법의 1 대 2 반복을 사용하는 중간은 핼리 방법의 단일 반복이다.이 경우 핼리의 방법은 시작 공식 $f{\displaystyle (}$ y${\displaystyle }$)${\displaystyle }$= 1 ${\displaystyle \frac{{y\mathrm{}}^{}}{}}$ ${\displaystyle \frac{{1\mathrm{}}^{}}{}}$/ 2${\displaystyle \frac{{}^{}}{}}$- ${\displaystyle x}$ ${\displaystyle {y\mathrm{}}^{}}$ ${\displaystyle {}^{}}$/ ${\displaystyle 2{}^{}}$= ${\displaystyle {0\mathrm{}}^{}}$ ${\displaystyle f(y)={\frac {1}{1/2}}-xy^{3/2}=0}$을(를) 사용하여 뉴턴의 방법을 적용하는 것과 같다$.$업데이트 단계는

${\displaystyle y_{n+1}=y_{n}-{\frac {f(y_{n}){f'(y_{n})}}}}=y_{n}\왼쪽 사진\frac {3+xy_{n}^{2}}:{1+3xy_{n}^{n}^{2}}\오른쪽),}$

여기서 구현은 $임시{\displaystyle }$ ${\displaystyle {변수}_{}^{}}$를 통해 x ${\displaystyle {\mathrm{}}_{}^{}}$n 2 {\$displaystyle xy_{n}^{2$}}회만$$ 계산해야 한다.

참고 항목

• 제곱근 계산 방법 § 부동소수점 표현에 따라 달라지는 근사치
• 매직넘버

메모들

참조

참고 문헌 목록

추가 읽기

• Kushner, David (August 2002). "The wizardry of Id". IEEE Spectrum. 39 (8): 42–47. doi:10.1109/MSPEC.2002.1021943.

외부 링크

• 0x5f3759df, Christian Plesner Hansen에 의한 알고리즘의 정확성과 일반성에 대한 추가 조사
• 쯔진3의 Fast InvQrt()의 기원
• Seez III 아레나 소스 코드(소프트웨어 헤리티지에 보관)
• DESMOS에서의 InvSqrt 구현
• "고속 역제곱근 — A Jein III 알고리즘"(유튜브)