반응 진행 운동 분석
Reaction progress kinetic analysis화학에서, 반응 진행 운동 분석(RPKA)은 화학 반응의 속도 법칙을 결정하고 반응 메커니즘의 해명에 도움을 주기 위해 사용되는 광범위한 운동 기법의 하위 집합이다. 반응 진행률 운동 분석을 안내하는 개념들이 새로운 것은 아니지만, 이 과정은 1990년대 후반 도나 블랙몬드 교수(현 스크립스 연구소)에 의해 공식화되었고, 그 이후 점점 널리 사용되고 있다. 관심 종에 비해 1개 이상의 시약을 압도적으로 초과하는 시약을 사용하는 더 일반적인 의사 1차 분석과 달리, RPKA는 종합적 관련 조건(즉, 비율법을 탐구하지 않을 때 반응에 사용된 것과 유사한 농도 및 시약 비율)에서 반응을 조사한다. 일반적으로 이 분석에는 여러 반응물질의 농도가 반응 과정에서 측정적으로 변화하고 있는 시스템이 포함된다. 메커니즘은 관련 종의 상대적 및 절대적 농도에 따라 달라질 수 있으므로, 이 접근방식은 전통적인 전술보다 공통적으로 이용되는 조건에서 반응 행동을 훨씬 더 잘 나타내는 결과를 얻는다. 또한, 시간에 따른 반응을 관찰하여 얻은 정보는 유도 기간, 촉매 비활성화 또는 메커니즘의 변화와 같은 예기치 않은 행동에 대한 통찰력을 제공할 수 있다.[1][2]
대응 진행률 모니터링
반응 진행 운동 분석은 시간에 따른 반응 변환을 정확하게 모니터링하는 능력에 의존한다. 이 목표는 아래에 설명되어 있는 가장 일반적인 기법에 의해 달성될 수 있다. 이러한 기법들은 때때로 미분(시간 경과에 따른 반응률 모니터링) 또는 적분(시간 경과에 따른 기질 및/또는 제품의 양을 모니터링)으로 분류되지만, 간단한 수학적 조작(차별화 또는 통합)은 둘 중 하나가 획득한 데이터의 상호 변환을 허용한다. 실시되는 기법과 관계없이, 일반적으로는 추가적인 독립적 방법으로 감시함으로써 관심 시스템에서 유효성을 확인하는 것이 유리하다.[2]
반응 진행 NMR
NMR 분광법은 종종 반응 진행률을 모니터링하기 위한 선택 방법이며, 여기서 비반응 표준에 대한 피크 통합의 변화로부터 기질 소비 및/또는 제품 형성이 시간 경과에 따라 관찰될 수 있다. 농도 데이터에서 시간 경과에 따른 반응 속도는 다항 적합의 파생 모델을 실험 곡선에 취함으로써 얻을 수 있다.[3] 반작용 진행률 NMR은 수집된 1차 데이터가 농도 대 시간에 비례하므로 적분 기법으로 분류할 수 있다.[2] 이 기법은 특이하고 격리된 제품 및/또는 반응제 피크인 명확하게 정의된 시스템에 매우 편리하지만, NMR 튜브에서 반응에 적합한 균일한 시스템을 요구하는 단점이 있다. NMR 관찰이 반응 매개체의 식별을 허용할 수 있지만, 반응 과정에서 특정 종의 존재는 반드시 생산적 과정에 개입하지는 않는다.[1] 그러나 반응 진행률 NMR은 종종 가변 온도에서 실행될 수 있으므로, 관측에 편리한 수준으로 반응 속도를 조정할 수 있다. 반응 진행의 활용 사례 NMR에는 Buchwald-Hartwig amination의 조사를 비롯한 주목할 만한 예가 많다(한 가지는 상당한 논쟁이 Buchwald-Hartwig amination의 기계론적 발전에 대한 최선의 접근법을 둘러싸고 있다는 점을 주목한다).t 기간 지정된 문서 및 참고 자료를 참조하십시오.)[4]
현장 FT-IR
시약이나 제품이 IR 스펙트럼 영역에서 독특한 흡광도를 보인다면, 상황에서 적외선 분광기를 사용하여 반응의 과정을 감시할 수 있다. 반응제 소비 및/또는 제품 형성률은 (맥주법을 적용하여) 시간의 경과에 따른 흡광도의 변화로부터 추상화될 수 있다. 반응제 및 제품 스펙트럼이 어느 정도 겹치는 경우라도, 현대의 계측 소프트웨어는 시간이 지남에 따라 관심 피크의 절대 흡광도에 급격한 변화가 있는 경우 상대적 기여를 정확히 설명할 수 있다. 현장에서 IR은 수집된 1차 데이터가 농도 대 시간에 비례하기 때문에 통합 기법으로 분류될 수 있다.[2] 이러한 데이터로부터, 실험 곡선에 다항 적합성의 적분을 단순히 취함으로써 시작 재료 또는 시간의 경과에 따른 제품 농도를 얻을 수 있다.[3] 상황 모니터링 기능을 갖춘 분광기의 가용성이 증가함에 따라 FT-IR은 최근 몇 년 동안 사용이 증가하고 있다. 주의의 예로는 부자연스러운 아미노산의 아미도-티우레아 촉매 비대칭 스트래커 합성 및 루이스 베이스 촉매 할로락톤화 및 사이클로테트리피케이션의 기계론적 분석이 있다.[5][6]
현장 UV-vis
위에서 설명한 상황 내 IR 실험과 유사하게, 시약이나 제품이 UV 스펙트럼 영역에서 독특한 흡광도를 보인다면 UV-visible 흡광도 분광법을 사용하여 반응의 과정을 감시할 수 있다. 반응제 소비 및/또는 제품 형성 속도는 (맥주 법칙의 적용에 의해) 시간의 경과에 따른 흡광도의 변화로부터 추상화될 수 있으며, 다시 통합 기법으로 분류된다.[2] 이용되는 스펙트럼 영역 때문에 UV-vis 기법은 순수 유기 반응보다 무기체나 유기체계에 더 많이 활용되고 있으며, 사마륨 바비에 반응의 탐사를 예로 들 수 있다.[7]
반응 열량계
반응에 대한 엔탈피 변화와 직접 관련이 있는 반응의 순간 열량이 모니터링되기 때문에 칼로리메트리(Calorimetry)를 사용하여 반응 과정을 모니터링할 수 있다. 반작용 칼로리 측정은 수집된 1차 데이터가 비율 대 시간에 비례하기 때문에 차등 기법으로 분류될 수 있다. 이러한 데이터로부터, 실험 곡선에 다항 적합성의 적분을 단순히 취함으로써 시작 재료 또는 시간의 경과에 따른 제품 농도를 얻을 수 있다.[2][8][9] 반응 열량 측정은 다른 여러 기법보다 덜 빈번하게 사용되지만, 촉매 선별을 위한 효과적인 도구로 사용된다는 것을 발견했다.[10] 반응 칼로리메트리는 또한 알데히드의[11] 프롤린산 α-아민화 및 팔라듐 촉매 부크왈드-하트위그 아민화 반응을 포함한 개별 반응의 기계론적 연구를 위한 효율적인 방법으로도 적용되었다.[4][12]
추가 기법
가스 크로마토그래피, HPLC, 질량 분광 분석은 모두 화합물의 혼합물(그리고 때로는 항균제)을 구별하는 뛰어난 기법이지만, 이러한 측정의 시간 분해능은 위에서 설명한 기법보다 덜 정밀하다. 그럼에도 불구하고,[13] 이러한 기법들은 여전히 사용되어 왔으며, 예를 들어, 반응의 이질적인 성질이 위에서 설명한 기법의 활용을 방해한 Heck 반응의 조사나, 유기 촉매에[14] 의한 SOMO 활성화가 그것들의 단점에도 불구하고, 우수한 교정 방법으로 작용할 수 있다.
데이터 조작 및 표시
반응 진행률 데이터는 기질 농도([A]t 대 시간(t) 또는 분수 변환(F) 대 시간(t)의 그래프로 가장 간단하게 표시될 수 있다. 후자는 다음과 같은 방법으로 농도/흡수 값을 부분 변환(F)으로 변환하기 위해 사소한 대수적 조작을 요구한다.
- F = [A]0 − [A]t/[A]0
기질 어디[A]0은 양, 흡광도,이나 집중력에 취항,[A]t은 양, 흡광도, 또는 그 시약의 집중 시간에, t. 불림 데이터 부분 변환한 것으로 여러 반응은 다른 절대 양이나 농도는 같은에 비교되는 것으로 진행 될 수 있도록 특별히 도움이 될 수 있는 선물. 복수오트의
데이터는 또한 일반적으로 반응률(v) 대 시간(t)의 그림으로 표시될 수 있다. 다시 말하지만, 간단한 대수적 조작이 필요하다. 예를 들어, 칼로리 실험은 다음을 제공한다.
- v = q/VΔH
여기서 q는 순간 열전달이고 ΔH는 반응의 알려진 엔탈피 변화, V는 반응량이다.[2]
반응 진행률 운동학 실험의 데이터는 비율(v) 대 기질 농도([S]) 그림을 통해 제시되는 경우가 많다. 이를 위해서는 위에서 설명한 [S] 대 t 및 v. t 그림 모두를 획득하고 결합해야 한다(단순 분화 또는 통합으로 다른 그림으로부터 하나를 얻을 수 있음). 이 조합은 x축을 따라 오른쪽에서 왼쪽으로 반작용 진행률을 판독하고 y축을 따라 아래에서 위로 반작용 속도를 판독하는 표준 곡선의 집합으로 이어진다.[2] 이러한 플롯은 종종 기본적인 운동 경향에 대한 시각적으로 설득력 있는 설명을 제공하지만, 차분 방법은 일반적으로 수치 속도 상수를 추출하는 데 우수하다. (아래 참조)
촉매 운동학 및 촉매 휴식 상태
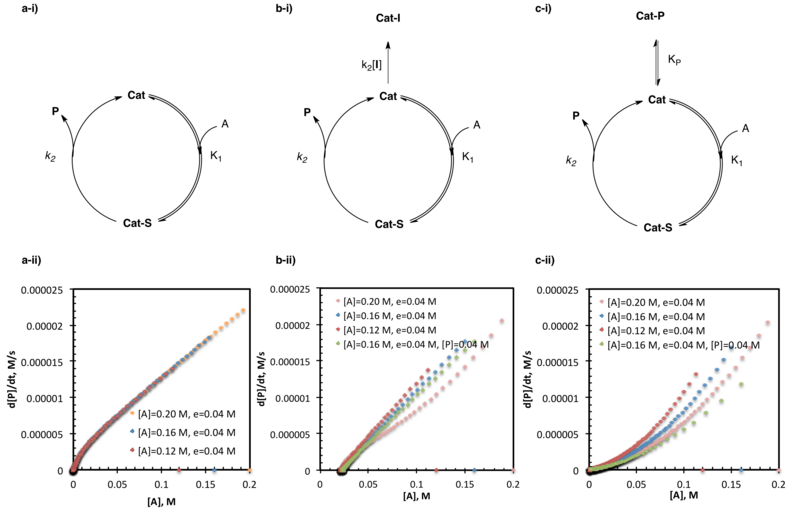
촉매역학에서는 (다른 상황에서) 많은 시스템의 동작을 설명하는 데 두 가지 기본적인 근사치가 유용하다. 평형전 및 안정상태 근사치가 유효한 상황은 반응 진행 운동 분석으로 구별할 수 있는 경우가 많으며, 두 상황은 촉매의 휴식 상태와 밀접하게 관련되어 있다.
정상 상태 근사치

정상 상태 조건에서 촉매와 기질은 가역적 연관성을 거친 후 촉매-하강 복합체를 비교적 빠르게 소비한다(제품에 대한 전방 반응과 결합되지 않은 촉매에 대한 역반응 둘 다). 정상 상태 근사치는 촉매-하강 복합체의 농도가 시간이 지남에 따라 변하지 않는다는 것을 나타낸다. 이 복합체의 총 농도는 형성 후 거의 즉시 제거되기 때문에 낮게 유지된다.[15] 정상 상태 속도 법칙은 시작 물질에서 상품으로 가는 데 필요한 속도 상수와 종을 모두 포함하고 있는 반면, 분모는 정상 상태 중간을 소비하는 전방 및 역방향 반응의 상대 속도를 설명하는 용어의 합으로 구성된다. 하나의 기질이 단일 중간재를 통해 하나의 제품으로 이동하는 가장 간단한 경우:
- d[P]/dt = k1k2[A][Cat]total/k−1 + k2
두 개의 기판이 순차적으로 결합되고 제품 릴리스가 이어지는 조금 더 복잡한 상황:
- d[P]/dt = kk123[A][B][Cat]/totalkk-1-2 + kk-13 + kk23[B]
점점 더 복잡한 시스템은 이 참조에서 설명한 알고리즘으로 간단히 설명할 수 있다.[16]
위에서 설명한 정상 상태 조건의 경우 촉매 휴식 상태는 결합되지 않은 형태(기질 결합 중간은 정의상 최소 농도에서만 존재하기 때문에)이다.[17]
평형 전 근사치

평형화 전 조건에서 촉매와 기질은 제품 형성과 방출로 이어지는 비교적 느린 단계에 앞서 빠르고 되돌릴 수 있는 결합을 거친다. 이러한 조건 하에서, 분자는 시작 물질에서 상품으로 가는 데 필요한 모든 비율 상수와 종으로 구성되며, 분모는 촉매가 존재하는 각 상태(그리고 1은 자유 촉매에 해당)를 설명하는 용어의 합으로 구성되는 "원 플러스" 비율 법칙으로 설명할 수 있다.[18] 하나의 기질이 단일 중간재를 통해 하나의 제품으로 이동하는 가장 간단한 경우:
- d[P]/dt = K1k2[A][Cat]/1 + K1[A]
두 개의 기판이 순서대로 결합되고 제품 릴리스가 뒤따르는 약간 더 복잡한 상황:
- d[P]/dt = KK122[A][B][Cat]/1 + K1[A] + KK12[A][B]
위에서 설명한 단순한 평형전 조건의 경우 촉매 휴식 상태는 (평형 상수의 크기에 따라) 기질 결합 복합체 전체 또는 일부다.
포화동력학
포화 상태는 평형 전 상태의 특수한 경우로 볼 수 있다. 검사한 기질 농도에서 촉매-하강 복합체의 형성은 빠르고 본질적으로 되돌릴 수 없다.[19] 촉매휴식상태는 전적으로 바운드 콤플렉스로 구성되며, [A]는 더 이상 요율법에 존재하지 않으며, [A]를 변경하면 이미 촉매가 완전히 결합되어 k가2 허용하는 한 빠르게 반응하기 때문에 반응률에 영향을 미치지 않을 것이다. 포화동력학의 가장 간단한 경우는 효소동력학을 위한 잘 연구된 Michaelis-Menten 모델이다.
촉매 휴식 상태의 변화


어떤 반응이 초기 변환 시 하나의 운동 동작을 보일 수 있지만, 그러한 행동은 다음과 같은 이유로 변할 수 있다.
- 기질 농도의 변화에 영향을 받는 촉매 휴식 상태의 변화
- 기질 또는 제품 농도의 영향을 받는 다중 또는 변경 메커니즘
- 촉매 활성화(시작 기간)
- 제품 억제
- 되돌릴 수 없는(또는 되돌릴 수 있는) 촉매 죽음
위에서 설명한 포화동력학의 경우, [A]가 [B]에 비해 큰 초과로 존재하지 않는 한, 포화 조건은 반응 시작 시에만 적용된다. 기질을 소비하면 농도가 낮아지고 결국 [A]는 [Cat]을 완전히 압도하기에는 더 이상 충분하지 않다. 이는 [A]의 0순서에서 다소 높은 순서의 비율(즉, 1순차, 2순차 등)으로 점진적인 변화로 나타난다. 이것은 또한 반응의 과정에 걸쳐 구속 형태에서 구속되지 않은 형태로 촉매 휴식 상태가 변화한 것으로도 설명할 수 있다.
단순히 반응을 느리게 하는 것 외에도, 반응 과정에 걸친 촉매 휴식 상태의 변화는 경쟁 경로나 과정을 야기할 수 있다. 제품에 접근하기 위한 여러 메커니즘이 존재할 수 있으며, 이 경우 반응의 조건이나 지점에 따라 촉매나 기질 순서가 변경될 수 있다. 반응 메커니즘의 변화를 위한 특히 유용한 탐구는 복수의 고정 변환 지점에서 정상화된 반응 속도 대 촉매 부하를 검사하는 것을 포함한다. 정규화된 반응 속도:
- k = v/[A]t
반응 과정에서의 기질 소비에 따라 조정되므로 촉매 부하에 의한 속도 변화만 관찰된다. 주어진 변환을 위한 촉매 부하에 대한 선형 의존은 해당 변환에서 촉매에 대한 1차 순서 의존성을 나타내며, 이와 유사하게 더 높은 순서 의존성에서 기인하는 비선형 그림을 상상할 수 있다. 한 변환점에서 다른 변환점으로의 선형성 또는 비선형성의 변화는 반응 과정에 걸쳐 촉매에 대한 의존성의 변화를 나타낸다. 반대로 다중 변환점(즉, 30, 50, 70%)에 걸쳐 보존된 플롯 영역의 선형성 또는 비선형성의 변화는 절대 촉매 농도에 기초한 촉매 의존성의 변화를 나타낸다.
반응 혼합물의 여러 성분과의 촉매 상호작용은 복잡한 운동 의존을 초래할 수 있다. 일반적으로 시스템에 대한 오프사이클 촉매-하향 또는 촉매-제품 상호작용은 "독성"으로 간주되지만(확실히 되돌릴 수 없는 복잡성의 경우) 오프사이클 종은 실제로 영구적인 비활성화로부터 촉매를 보호하는 경우가 존재한다.[21][22] 어느 경우든 촉매 휴식 상태의 역할을 이해하는 것이 필수적인 경우가 많다.[3][11]
동일과잉실험
반응 진행률 운동 분석에 가장 큰 관심을 보이는 변수 매개변수는 어금니 단위로 주어진 한 기질이 다른 기질에 비해 과도함(e)이다. 한 반응에서 두 종의 초기 농도는 다음과 같이 정의할 수 있다.
- [B]0 = [A]0 + e
그리고 1:1 반응 스토이치측정법을 가정할 때, 다른 기질보다 한 기질 초과분은 다음과 같이 전체 반응 과정 동안 정량적으로 보존된다.[3]
- [B]t = [A]t + e
유사한 집합은 높은 순서의 스토이치측정법으로 반응하기 위해 구성될 수 있으며, 이 경우 초과분은 반응 과정에 따라 예측 가능하게 변화한다. e는 임의의 값(양, 음 또는 0)일 수 있지만, 일반적으로 기질 1 등가보다 크기가 작은 양의 값이나 음의 값이 반응 진행 운동 분석에서 사용된다. (의사 제로 순서 운동학에서는 기질 1 등가보다 크기가 훨씬 큰 초과 값을 사용할 수 있다.)
초과(e)의 매개변수를 정의하면 초기 농도가 다른 운동 실험의 둘 이상의 런을 수행하는 동일과잉 실험의 구성을 허용하지만, 동일과잉은 어느 지점에서든 인위적으로 반응에 들어갈 수 있다. 이러한 실험은 촉매 반응의 RPKA에 매우 중요한데, 이는 아래에 자세히 설명되어 있는 촉매 활성화(유도 기간), 촉매 비활성화 및 제품 억제를 포함한 많은 기계론적 가능성을 조사할 수 있기 때문이다.[2][3]
촉매 전환 주파수 결정
추가적인 기계론적 조사에 앞서 촉매에 대한 관심 반응의 운동 의존도를 결정하는 것이 중요하다. 촉매의 회전 주파수(TOF)는 촉매 농도로 정규화된 반응 속도로 표현할 수 있다.
- TOF = v/[Cat]
이 TOF는 절대 촉매 농도가 변화하는 두 개 이상의 동일한 초과 실험에 의해 결정된다. 반응 과정에서 촉매 농도가 일정하기 때문에 결과 플롯은 불변의 값으로 정규화된다. 결과 플롯이 완벽하게 겹쳐진다면, 그 반응은 사실 촉매에서 1차적인 것이다. 반응이 오버레이되지 않으면 고차 프로세스가 진행되며 여기에서 설명하는 것보다 더 상세한 분석이 필요하다.[3] 여기에 기술된 정상화 오버레이 조작은 원시 데이터를 해석하는 하나의 접근법일 뿐이라는 점도 주목할 필요가 있다. 관측된 운동 동작을 시뮬레이션 속도 법칙에 적합시킴으로써 동등하게 유효한 결과를 얻을 수 있다.
촉매 활성화 및 비활성화 탐색

위에서 설명한 바와 같이 기판의 절대 농도를 변경하면서 (e) 상수를 유지한 두 개 이상의 실험으로 동일과과잉 실험을 실시한다(이 경우 촉매도 기질로 취급된다). 이 구조는 등가물의 수를 유발하므로 각 시약/촉매의 몰 백분율이 반응마다 다르다는 점에 유의하십시오.[3] 이러한 실험은 한 실험의 초기 농도(절편 반응)가 다른 중간 시간 t에서 예상되는 농도에 직접 매핑되도록 선택되기 때문에 어느 지점에서나 인위적으로 반응을 "입력"할 수 있다. 위에서 상세히 설명한 비율 대 기질 농도 그림으로 설명되는 반응 진행률이 그 가로채기 지점에서 앞으로 서로 직접 매핑될 것으로 예상할 수 있다. 단, 이는 그 간섭 이전에 활성 기질/촉매 농도의 변화(촉매 활성화, 촉매 비활성화 또는 제품 억제 등)에 의해 반응 속도가 변경되지 않는 경우에만 참이다.[2][3]
동일하지만 다른 초기 기질 하중을 가진 여러 실험의 완벽한 오버레이는 활성 기질/촉매 농도의 변화가 반응 과정 동안 발생하지 않음을 시사한다. 그림의 오버레이 실패는 일반적으로 반응 조건 하에서 촉매 활성화, 비활성화 또는 제품 억제를 나타낸다. 이러한 경우는 서로 상대적인 반응 진행 곡선의 위치에 의해 구별될 수 있다. 비율 대 기질 농도 그림에 대한 상위 반응(동일한 기질 농도에서의 낮은 속도) 아래에 놓여 있는 반응을 가로채는 반응은 반응 조건 하에서 촉매 활성화를 나타낸다. 비율 대 기질 농도 그림에 대한 상위 반응(동일한 기질 농도에서의 더 빠른 속도)이 위에 놓여 있는 반응을 가로채는 것은 반응 조건 하에서 촉매 비활성화를 나타낸다. 제품 억제와 다른 형태의 촉매 사망을 구별하기 위해 추가 실험이 필요하다.[2]
위에서 설명한 가로채기 반응과 상위 반응 사이의 중요한 차이점은 가로채기 지점의 상위 반응에 어느 정도의 제품이 존재한다는 것이다. 제품 억제는 오래 전부터 많은 시스템의 촉매 효율에 영향을 미치는 것으로 알려져 있으며, 같은 과도 실험의 경우 가로채기와 부모 반응이 오버레이되는 것을 방지한다. 위에서 설명한 것과 같은 과도 실험으로는 촉매 불활성화를 특정 원인에 귀속시킬 수 없지만, 제품 억제는 동일한 하위 반응에서 상위 반응에 존재할 것으로 예상되는 제품의 양을 모방하도록 설계된 제품의 일부 초기 양을 가로채기 반응에 추가하는 추가 실험을 통해 조사할 수 있다.집중력을 높이다 동일한 제품 조건에서 비율 대 기질 농도 그림의 완벽한 중첩은 사용된 반응 조건에서 제품 억제가 발생한다는 것을 나타낸다. 속도 대 기질 농도 그림이 동일한 제품 조건에서 오버레이되지 않는 것은 제품 억제를 배제하지 않지만, 적어도 다른 촉매 비활성화 경로도 활성 상태여야 함을 나타낸다.
촉매 비활성화 및 제품 억제를 조사하는 동일과잉 실험은 반응 진행 운동 분석에서 가장 널리 사용되는 응용 분야 중 하나이다. 문헌에 수록된 수많은 사례들 중에는 알데히드의 아미노 알코올 촉매 아연 알킬화의 조사,[23] 부자연스러운 아미노산의 아미도-티우레아 촉매 비대칭 스트렉커 합성,[5] 유기 촉매의 SOMO 활성화가 포함되어 있다.[14]
반응계측법 결정
속도 상수를 추출하는 차등 방법
시간에 따른 반응 진행률을 모니터링하여 얻을 수 있는 풍부한 데이터가 현대의 컴퓨팅 방법의 힘과 결합되면서, 시뮬레이션된 반응 경로의 통합 속도 법칙을 시간에 따른 반응 진행률의 적합성에 매핑하면서 속도 법칙을 수치적으로 평가하는 것이 상당히 간단해졌다. 오차 전파 원리 때문에, 비율 상수와 비율 법칙은 그래픽 비율 방정식의 구성(위)보다 불확실성이 현저히 낮은 이러한 미분 방법에 의해 결정될 수 있다.[9]
상이과 실험
RPKA는 전체 반응 과정에 걸쳐 비율을 관측할 수 있지만, 동일한 초과 실험만 수행해도 해당 속도 상수를 결정하기 위한 충분한 정보를 제공하지 않는다. 알 수 없는 모든 요금 상수에 대해 해결할 수 있는 충분한 독립적 관계를 구축하기 위해서는 초과가 다른 시스템을 검토할 필요가 있다.
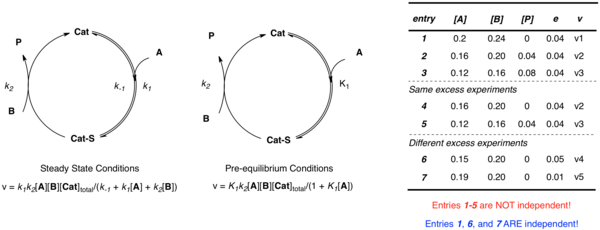
위에서 설명한 간단한 예를 다시 생각해 보십시오. 촉매가 기판 A와 연결된 다음 B와 반응하여 제품 P와 자유 촉매를 형성하십시오. 적용된 근사치에 관계없이 시스템을 정의하려면 복수의 독립 매개변수(전 평형화의 경우 k2, K1, 안정 상태의 경우 k1, k−12)가 필요하다. 서로 다른 농도에서 미지의 내용을 설명하기 위해 복수의 방정식을 구성하는 것을 상상할 수 있지만, 동일한 과도 실험 [A]와 [B]에서 데이터를 얻었을 때 다음과 같이 독립적이지 않다.
- e = [B] − [A]
e의 다른 값을 사용한 다중 실험은 실험 속도와 농도의 측면에서 다중 독립 속도 상수를 정의하는 다중 독립 방정식을 확립하기 위해 필요하다. 그런 다음 비선형 최소 제곱 분석을 사용하여 그러한 방정식에 대해 알 수 없는 비율 상수의 최적 적합치를 구할 수 있다.
그래픽 속도 법칙
운동가들은 역사적으로 요율 상수를 추정하기 위해 요율 데이터의 선형화에 의존해 왔으며, 아마도 마이클리스-멘텐 방정식의 표준 라인위버-버크 선형화의 광범위한 사용에서 가장 잘 입증되었을 것이다.[24] 선형화 기법은 복잡한 곡선을 맞출 수 있는 컴퓨팅 기법이 등장하기 전에는 특히 중요했으며, 직관적으로 간단한 표현으로 인해 키네틱스의 주요 요소로 남아 있다.[2] 선형화 기법은 대체 수치 기법과 관련된 큰 오차를 도입하기 때문에 수치 속도 상수를 추출하는 데 사용해서는 안 된다는 점에 유의해야 한다. 그러나 그래픽 속도 법칙은 그래프의 육안 검사가 당면한 반응에 관한 기계론적 통찰력을 제공할 수 있도록 선형화된 데이터의 직관적인 표시를 유지한다. 그래픽 속도 법칙의 근거는 위에서 논의한 비율(v) 대 기질 농도([S]) 그림에 있다. 예를 들어, 서로 다른 과도현상 실험과 관련하여 논의된 간단한 주기에서는 v/[A] 대 [B] 대 [B] 및 그 쌍둥이 v/[B] 대 [A]의 플롯이 각 시약 순서에 대한 직관적인 통찰력을 제공할 수 있다. 초과가 다른 여러 실험에 대한 v/[A] 대 [B] 오버레이 그림의 경우 데이터는 [A]에 대한 1차 의존도와 일치한다. v/[B] 대 [A]의 플롯도 마찬가지일 수 있다. 오버레이는 [B]에 대한 1차 의존도와 일치한다. 이러한 그래픽 속도 법칙의 비중첩성 결과는 검증한 기판에 대한 높은 질서의 의존성을 나타낸다. 블랙몬드는 일련의 그래픽 속도 방정식으로 서로 다른 과도 실험의 결과(여기서 개조한 흐름도로 제시)를 제시할 것을 제안했지만, 그녀가 제안한 방법은 운동 관계를 표시하기 위한 가능한 여러 방법 중 하나일 뿐이라는 점에 유의해야 한다. 또한, 그래픽 속도 법칙의 표시는 복잡한 운동 데이터를 표시하는 시각적으로 단순한 방법으로 간주될 수 있지만, 정확하고 정량적인 속도 상수와 반응 순서를 추출하기 위해 미분 또는 기타 엄격한 수치 방법에 의한 분석에 원시 운동 데이터를 적합시키는 것이 필요하다.[2][3]
반응 스토이치측정법 및 메커니즘
운동학적 분석이 지상 상태에 비해 턴오버 제한 전환 상태의 정지계측을 결정하는 강력한 도구임에도 불구하고 모든 기계론적 질문에 답할 수는 없다는 점에 유의해야 한다. 특히 촉매 조건에서 두 메커니즘을 키네틱적으로 구별할 수 없는 것이 가능하다. 철저한 기계론적 평가를 위해서는 선형 자유 에너지 관계 평가, 동위원소 효과 연구, 계산 분석 또는 다수의 대체 접근법과 같은 다른 형태의 분석과 함께 촉매 프로세스와 그 개별 단계(가능한 경우)의 운동학적 분석을 수행할 필요가 있다. 마지막으로, 어떤 기계론적 가설도 증명될 수 없다는 것을 주목하는 것이 중요하다; 대안적 기계론적 가설은 반증될 수 밖에 없다. 따라서 어떠한 조사도 가설 중심의 방식으로 진행하는 것이 필수적이다. 합리적인 대안을 실험적으로 반증해야만 주어진 가설에 대한 지지가 강화될 수 있다.[25]
참고 항목
참조
- ^ a b Hartwig, J. F. (2010). Organotransition Metal Chemistry: From Bonding to Catalysis. Mill Valley, California: University Science Books. ISBN 978-1-891389-53-5.
- ^ a b c d e f g h i j k l m Blackmond, D. G. (2005). "Reaction Progress Kinetic Analysis : A Powerful Methodology for Mechanistic Studies of Complex Catalytic Reactions". Angew. Chem. Int. Ed. 44 (28): 4302–4320. doi:10.1002/anie.200462544. PMID 15997457.
- ^ a b c d e f g h i Blackmond, D. G.; Ropic, M.; Stefinovic, M. (2006). "Kinetic Studies of the Asymmetric Transfer Hydrogenation of Imines with Formic Acid Catalyzed by Rh−Diamine Catalysts". Org. Process Res. Dev. 10 (3): 457–463. doi:10.1021/op060033k.
- ^ a b Shekhar, S.; Ryberg, P.; Hartwig, J. F.; Mathew, J. S.; Blackmond, D. G.; Strieter, E. R.; Buchwald, S. L. (2006). "Reevaluation of the Mechanism of the Amination of Aryl Halides Catalyzed by BINAP-Ligated Palladium Complexes". J. Am. Chem. Soc. 128 (11): 3584–3591. doi:10.1021/ja045533c. PMID 16536531.
- ^ a b Zuend, S. J.; Jacobsen, E. N. (2009). "Mechanism of Amido-Thiourea Catalyzed Enantioselective Imine Hydrocyanation: Transition State Stabilization via Multiple Non-Covalent Interactions". J. Am. Chem. Soc. 131 (42): 15358–15374. doi:10.1021/ja9058958. PMC 2783581. PMID 19778044.
- ^ Denmark, S. D.; Burk, M. T. (2010). "Lewis base catalysis of bromo- and iodolactonization, and cycloetherification". Proc. Natl. Acad. Sci. 107 (48): 20655–20660. Bibcode:2010PNAS..10720655D. doi:10.1073/pnas.1005296107. PMC 2996424. PMID 20705900.
- ^ Choquette, K. A.; Sadasivam, D. V.; Flowers, R. A. (2011). "Catalytic Ni(II) in Reactions of SmI2: Sm(II)- or Ni(0)-Based Chemistry?". J. Am. Chem. Soc. 133 (27): 10655–10661. doi:10.1021/ja204287n. PMID 21619012.
- ^ Mathew, J. S.; Klussmann, M.; Iwamura, H.; Valera, F.; Futran, A; Emanuelsson, E. A. C.; Blackmond, D. G. (1999). "Investigations of Pd-Catalyzed ArX Coupling Reactions Informed by Reaction Progress Kinetic Analysis". J. Org. Chem. 71 (13): 4711–4722. doi:10.1021/jo052409i. PMID 16776495.
- ^ a b Steel, C.; Naquvi, K. R. (1991). "Differential method in chemical kinetics". J. Phys. Chem. 95 (26): 10703–10718. doi:10.1021/j100179a037.
- ^ Blackmond, D. G.; Rosner, T.; Pfaltz, A. (1999). "Comprehensive Kinetic Screening of Catalysts Using Reaction Calorimetry". Org. Process Res. Dev. 3 (4): 275–280. doi:10.1021/op990024u.
- ^ a b Hein, J. E.; Armstrong, A.; Blackmond, D. G. (2011). "Kinetic Profiling of Prolinate-Catalyzed α-Amination of Aldehydes". Org. Lett. 13 (16): 4300–4303. doi:10.1021/ol201639z. PMID 21761822.
- ^ Singh, U. K.; Strieter, E. R.; Blackmond, D. G.; Buchwald, S. L. (2002). "Mechanistic Insights into the Pd(BINAP)-Catalyzed Amination of Aryl Bromides: Kinetic Studies under Synthetically Relevant Conditions". J. Am. Chem. Soc. 124 (47): 14104–14114. doi:10.1021/ja026885r. PMID 12440909.
- ^ Herrmann, W. A.; Brossmer, C.; Reisinger, C. P.; Riermeier, T. H.; Öfele, K.; Beller, M. (1997). "Palladacycles: Efficient New Catalysts for the Heck Vinylation of Aryl Halides". Chem. Eur. J. 3 (8): 1357–1364. doi:10.1002/chem.19970030823.
- ^ a b Devery, J. J.; Conrad, J. C.; MacMillan, D. W. C.; Flowers, R. A. (2010). "Mechanistic Complexity in Organo–SOMO Activation". Angew. Chem. Int. Ed. 49 (35): 6106–6110. doi:10.1002/anie.201001673. PMC 3065936. PMID 20632343.
- ^ Srinivasan, Bharath (2020-10-08). "Explicit Treatment of Non Michaelis-Menten and Atypical Kinetics in Early Drug Discovery". ChemMedChem. 16 (6): 899–918. doi:10.1002/cmdc.202000791. ISSN 1860-7179. PMID 33231926. S2CID 227157473.
- ^ Gilbert, H. F. (1977). ""Rule of thumb" for deriving steady state rate equations". J. Chem. Educ. 54 (8): 492–493. Bibcode:1977JChEd..54..492G. doi:10.1021/ed054p492.
- ^ "4.12: Steady-State Approximation". 22 July 2015.
- ^ Helfferich, F. G. (1989). "Systematic approach to elucidation of multi-step reaction networks". J. Phys. Chem. 93 (18): 6676–6681. doi:10.1021/j100355a022.
- ^ Srinivasan, Bharath (2020-09-27). "Words of advice: teaching enzyme kinetics". The FEBS Journal. 288 (7): 2068–2083. doi:10.1111/febs.15537. ISSN 1742-464X. PMID 32981225.
- ^ Zuend, S. J.; Jacobsen, E. N. (2007). "The mechanistic scheme and kinetic data are adapted from independent kinetic simulations using the rate and equilibrium constants reported for the amino-thiourea catalyzed cyanosilylation of ketones". J. Am. Chem. Soc. 129 (51): 15872–15883. doi:10.1021/ja0735352. PMID 18052247.
- ^ List, B. (2002). "Proline-catalyzed asymmetric reactions". Tetrahedron. 58 (28): 5573–5590. doi:10.1016/S0040-4020(02)00516-1.
- ^ Seebach, D.; Beck, A. K.; Badine, D. M.; Limbach, M.; Eschenmoser, A.; Treasurywala, A. M.; Hobi, R.; Prikoszovich, W. (2007). "Are Oxazolidinones Really Unproductive, Parasitic Species in Proline Catalysis? – Thoughts and Experiments Pointing to an Alternative View". Helv. Chim. Acta. 90 (3): 425–471. doi:10.1002/hlca.200790050.
- ^ Rosner, T.; Sears, P.J.; Nugent, W. A.; Blackmond. D.G. (2000). "Kinetic Investigations of Product Inhibition in the Amino Alcohol-Catalyzed Asymmetric Alkylation of Benzaldehyde with Diethylzinc". Org. Lett. 2 (16): 2511–2513. doi:10.1021/ol006181r. PMID 10956534.
- ^ Lineweaver, H.; Burke, D. (1934). "The determination of enzyme dissociation constants". J. Am. Chem. Soc. 56 (3): 658–666. doi:10.1021/ja01318a036.
- ^ Platt, J. R. (1964). "Strong Inference". Science. 146 (3642): 347–353. Bibcode:1964Sci...146..347P. doi:10.1126/science.146.3642.347. PMID 17739513.