기본 재생산 번호
Basic reproduction number역학으로 보면, 기본 복제 숫자 또는 기본적인 생식 수(때로는 기본적인 생식 비율 또는 기본적인 생식율), 감염의 R0{\displaystyle R_{0}}(라고 선언했다 R0또는 R0)[1]를 설명하는 경우 바로 사건에 의해 모든 개인이 될 수 있는 인구에 생성된 예상 번호입니다.es감염을 감지할 [2]수 있는이 정의는 다른 어떤 개인도 감염되거나 예방접종을 받지 않는다고 가정한다(자연적으로 또는 예방접종을 통해).호주 보건부의 정의와 같은 일부 정의는 "질병 전염에 대한 어떤 의도적인 개입"의 부재를 추가한다.[3]기본적인 생식 번호 반드시 그 사례들은 인구의 사이프러스도 없는 현재 상태에서 생성된 수를 효과적인 생식 수 R{R\displaystyle}(보통 쓰여진 Rt{\displaystyle R_{t}}[시간 t], 가끔 Re{\displaystyle R_{e}})[4]과 같다.e감염되지 않은 상태 은(는) 차원 없는 수(감염되는 사람당 감염되는 사람)로, 시간−1 단위 [5]또는 시간 단위(두 배 시간 단위)를 가지지 않는다.[6]
는 환경 조건과 감염 인구의 행동과 같은 다른 요인에 의해서도 영향을 받기 때문에 병원체의 생물학적 상수가 아니다. 값은 대개 수학적 모델에서 추정되며, 추정 값은 사용된 모델과 다른 모수의 값에 따라 달라진다.따라서 문헌에 제시된 값은 주어진 맥락에서만 타당하며, 구식 값을 사용하거나 다른 모델에 기초한 값을 비교하지 않는 것이 좋다.[7] 그 자체로는 감염이 모집단에 얼마나 빨리 퍼지는지 추정할 수 없다.
의 가장 중요한 용도는 신종 감염병이 모집단에 퍼질 수 있는지 여부를 결정하고, 질병 근절을 위해 예방접종을 통해 모집단의 몇 비율을 예방접종해야 하는지를 결정하는 것이다.일반적으로 사용되는 감염 에서 > 1 }이가) 집단에서 감염을 시작할 수 있지만, R < 1}. 으로 < 의 값이 클수록 전염병을 통제하기가 어렵다단순한 모델들에게는 효과적으로(의미 감염에 취약하지 않)면역력을 가질 감염의 지속적인 확산을 막기 위해 필요한 인구의 비율 1/R0{1-1/R_{0\displaystyle}}.[8]1−보다 큰 거고 반대로, 감염에 대한 풍토병에 취약한 채 남아 있는 인구의 비율이다.e는 1/ 입니다
기본 생식 수는 감염자의 감염 기간, 미생물의 전염성, 감염자가 접촉하는 인구의 취약인구의 수 등 몇 가지 요인에 의해 영향을 받는다.
역사
기본 재생산 개념의 뿌리는 로널드 로스, 알프레드 로트카 등의 작품을 통해 추적할 수 있지만 역학에서 처음으로 현대적으로 응용한 것은 1952년 말라리아 [10]확산의 인구 모델을 구축한 조지 맥도널드에 의해서였다.[9]그의 작품에서 그는 기본 재생산률을 Z 으로 부르고 이 문맥에서 "Rate"는 1인당 평균으로 나타냈는데, 이것은 에 Z0 {\0}}}}를 차원이 없게 만든다.이것은 시간의 단위당 의미에서만 "비율"을 이해하는 사람에게 오도될 수 있기 때문에, 현재 "숫자"나 "비율"이 선호되고 있다.[citation needed]
특정 사례의 정의
접촉률 및 감염기간
감염자가 단위 시간당 평균 의 감염 생성 접점을 만들고 평균 감염 기간은 이라고 가정해 보십시오 그러면 기본 재생산 번호는 다음과 같다.
서 c는 감염되기 쉬운 개인과 감염된 개인 간의 접촉 비율이며 T 는 전염성, 즉 접촉에 의해 감염될 확률이다.또한 (동물이 흔히 그렇듯이) 감염 개인을 발견하여 격리, 치료 또는 제거함으로써 감염 기간 을(를) 가능한 빨리 단축할 수 있다.[citation needed]
다양한 잠재 기간과 함께
잠복기는 전염병과 질병 발현 사이의 전이 시간이다.잠복기가 서로 다른 질병의 경우, 질병으로 전이되는 각 시간에 대한 재생산 수의 합으로 기본 재생산 수를 계산할 수 있다.그 예로는 결핵(TB)이 있다.TB의 단순한 모델로부터 다음과 같은 재생 번호를 계산한 블로워 및 공저자:[12]
이질적인 인구
동질적이지 않은 모집단에서는 의 정의가 더 미묘하다.이 정의는 일반적인 감염자가 일반 개인이 아닐 수 있다는 사실을 설명해야 한다.극단적인 예로, 개인의 작은 부분이 서로 완전히 섞이고 나머지 개인은 모두 고립되어 있는 모집단을 생각해 보자.질병은 무작위로 선정된 개인이 2차 환자 1명 미만으로 이어질 수 있지만 완전히 혼합된 부분에 퍼질 수 있다.대표적인 감염자가 완전히 혼합된 부분에 있어 성공적으로 감염을 일으킬 수 있기 때문이다.일반적으로 전염병 초기에 감염된 개인이 전염병 후기에 감염된 개인보다 평균적으로 전염될 확률이 높거나 낮다면, 의 계산은 이러한 차이를 설명해야 한다.이 경우 R 에 대한 적절한 정의는 "일반적인 감염자가 생성하는 완전히 취약한 모집단에서 생성된 2차 사례의 예상 수"[14]이다.
기본 재생산 번호는 시간 경과에 따른 알려진 비율로서 계산할 수 있다: 감염성 개인이 단위 시간당 다른 사람과 접촉하는 경우 }명, 그 모든 사람이 질병에 감염된 것으로 가정하는 경우, 그리고 질병의 평균 감염 이 1㎛ {1 t t.hen 기본 생식번호는 0 = }}}}}}일 뿐 일부 질병은 가능한 여러 가지 잠복기를 가지고 있는데, 이 경우 전체 질병의 생식번호는 질병으로 전환되는 각 시간에 대한 생식번호의 합이다.예를 들어 [12]블로워 등은 두 가지 형태의 결핵 감염을 모델로 한다. 빠른 경우에는 노출 직후에 증상이 나타나고 느린 경우에는 초기 노출 후 몇 년 후에 증상이 나타난다(내생적 재활성화).전체 재생산 번호는 두 가지 형태의 수축의 합이다. = A + L
추정 방법
기본 재생산 번호는 상세한 전송 체인을 조사하거나 유전체 염기서열을 통해 추정할 수 있다.그러나 역학 모델을 사용하여 계산하는 경우가 가장 많다.[15]전염병 발생 시 일반적으로 시간 에 걸쳐 진단된 감염 ( t) 의 수가 알려져 있다.전염병의 초기 단계에서는 성장이 기하급수적으로 증가하고, 로그 성장률이 높다.
지수 성장에서 은(는) 과 같이 d T_}를 두 배로 증가시키는 것과 관련이 있다.
심플 모델
만약 개인이 감염 후 0 0의 새로운 개인을 시킨다면, 시간이 지남에 따라 감염자의 수가 증가하게 된다
를 들어, = d{\= .- {\.183}=를 하면= 2.{\2.5
이(가) 시간에 종속된 경우
잠복 감염 기간, 진단 후 격리
이 모델에서 개별 감염은 다음과 같은 단계를 가진다.
- 노출: 개인은 감염되었지만 아무런 증상이 없고 아직 다른 사람을 감염시키지 않는다.노출 상태의 평균 지속시간은 E 이다
- 잠재 전염병: 개인은 감염되었고, 증상은 없지만, 다른 사람을 감염시킨다.잠복 감염 상태의 평균 지속시간은 I 이다개인은 이 기간 동안 R 다른 개인을 감염시킨다.
- 진단 후 격리: 감염자를 격리하는 등 추가 감염을 방지하기 위한 조치를 취한다.
이것은 SEIR 모델이며 은(는) 다음과 같은 형태로[16] 작성될 수 있다.
특별한 경우 = 이 에서는 R = + K E{\이 나오며 위의 단순 모델과는 다르다( 0= exp E){\exp예를 들어, 한 값 = 5 과 K= d- }을 사용하면 0= 9 }=1}=1}=1}=1을 찾을 수 있다 2.5 2의 참 값보다는 그 차이는 기저 성장 모델의 미묘한 차이 때문이다; 위의 행렬 방정식은 새로 감염된 환자가 현재 이미 감염에 기여하고 있는 반면, 사실 감염은 }에서 감염된 숫자 때문에만 발생한다고 가정한다. 전.좀 더 정확한 처리를 위해서는 지연 미분 방정식을 사용해야 한다.[17]
유효 재생수
사실, 인구의 다양한 비율은 주어진 질병에 언제든지 면역이 된다.이를 설명하기 위해 유효 재생산 e R 을(를) 사용한다. 는 부분적으로 취약한 모집단의 시간 t에서 단일 감염자에 의해 발생하는 평균 신규 감염 수입니다. 에 취약한 모집단의 분수 S를 곱하면 알 수 있다.이 있는 모집단의 분율(즉 취약 모집단 S)이 증가하여 e e}}이 기본 SIR 시뮬레이션에서 1 이하로 떨어지면 "herd 면역"이 달성되어 모집단에서 발생하는 경우의 수가 점차 0으로 감소한다.[18][19][20]
R의0 한계
대중매체에 을 사용함으로써 그 의미를 오해하고 왜곡시켰다. 은(는) 여러 가지 다른 수학적 모델에서 계산할 수 있다.이들 각각은 R 의 다른 추정치를 제공할 수 있으며 이 추정치는 해당 모델의 맥락에서 해석해야 한다.따라서 상이한 감염성 물질의 전염성은 불변성 가정으로 0을 재계산하지 않고는 비교할 수 없다.과거 발생에 대한 값은 동일한 질병의 현재 발생에 유효하지 않을 수 있다.일반적으로 0< 1 {\0}<1}, < 1{\1 만약 R > 만약 0 > 1 {\displaystyle R_{0}1}1 발생이 확대되더라도 R 0을 임계값으로 사용할 수 있다.일부 모델의 경우 R < 의 이 여전히 자가 발생으로 이어질 수 있다.이것은 특히 말라리아와 같이 호스트 사이에 중간 벡터가 있는 경우에 문제가 된다.[21]따라서 " 알려진 전염병의 R 0 표의 값 간 비교는 주의 깊게 실시해야 한다.
은(는) 예방접종이나 기타 인구 민감도 변화를 통해 수정할 수 없지만, 여러 생물학적, 사회적 행동적, 환경적 요인에 따라 달라질 수 있다.[7]일부 역사적 정의에서 비약물학적 개입을 포함하여 질병 전염을 줄이기 위한 의도적인 개입은 배제하지만,[22][7] 물리적 거리 및 기타 공공 정책 또는 사회적 개입에 의해서도 수정될 수 있다.[3]그리고 실제로 비약학적 개입이 에 포함되는지는 종종 종이, 질병, 그리고 어떤 개입이 연구되고 있다면 어떻게 되는가 하는 것에 달려 있다.[7]이는 0{\이 상수가 아니기 때문에 혼동을 유발하는 반면, "없음" 첨자가 있는 대부분의 수학 파라미터는 상수이기 때문이다.
은(는) 많은 요인에 따라 달라지는데, 그 중 상당수는 추정할 필요가 있다.이러한 요소들은 R 의 추정치에 불확실성을 더한다 이러한 요소들 중 많은 것들이 공공 정책을 알리는 데 중요하지 않다.따라서 공공 정책은 과와) 유사한 지표에 의해 더 잘 제공될 수 있지만, 이중화 시간이나 반감기와 추정하기 더 쉬운 지표( / 2 [23][24]
방법 R0{\displaystyle R_{0}계산에 사용되는}, 야코비 행렬의 가장 큰 고유 값이 생존 기능이 포함되어 있는 고질적 평형의 고유한 성장 rate,[26]생활로부터 차세대 method,[25]계산 susceptibles의 풍토적 균형에 해당, inf의 평균 연령.ection[27]최종 크기 방정식을 참조하십시오.같은 미분방정식으로 시작한다고 해도 이러한 방법들 중 거의 서로 동의하는 것은 없다.[21]실제로 2차 감염의 평균 수를 계산하는 사람은 훨씬 적다. 은 현장에서 거의 관찰되지 않으며 보통 수학적 모델을 통해 계산되기 때문에, 이는 그 유용성을 심각하게 제한한다.[28]
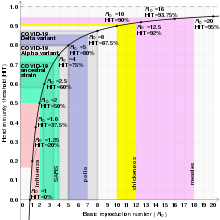
각종 감염병 표본값
| 병 | 전송 | R0 | 히트[a] |
|---|---|---|---|
| 홍역 | 에어로졸 | 12–18[29][7] | 92–94% |
| 수두(바리셀라) | 에어로졸 | 10–12[30] | 90–92% |
| 유행성 이하선염 | 호흡기방울 | 10–12[31] | 90–92% |
| COVID-19(오미크론 변종) | 호흡기방울 | 7[32] | 86% |
| 풍진 | 호흡기방울 | 6–7[b] | 83–86% |
| 소아마비 | 대변-도덕로 | 5–7[b] | 80–86% |
| 백일해 | 호흡기방울 | 5.5[37] | 82% |
| COVID-19(델타 변종) | 호흡기 방울 및 에어로졸 | 5.1[38] | 80% |
| 천연두 | 호흡기방울 | 3.5–6.0[39] | 71–83% |
| COVID-19(Alpha 변종) | 호흡기 방울 및 에어로졸 | 4–5[40][medical citation needed] | 75–80% |
| HIV/에이즈 | 체액 | 2–5[41] | 50–80% |
| COVID-19(항상 변형률) | 호흡기 방울 및 에어로졸[42] | 2.9 (2.4–3.4)[43] | 65% (58–71%) |
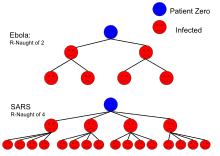
| 사스 | 호흡기방울 | 2–4[44] | 50–75% |
| 디프테리아 | 침 | 2.6 (1.7–4.3)[45] | 62% (41–77%) |
| 감기 | 호흡기방울 | 2–3[46][medical citation needed] | 50–67% |
| 인플루엔자(1918년 유행성 변종) | 호흡기방울 | 2[47] | 50% |
| 에볼라(2014년 발생) | 체액 | 1.8 (1.4–1.8)[48] | 44% (31–44%) |
| 인플루엔자(2009년 유행성 변종) | 호흡기방울 | 1.6 (1.3–2.0)[2] | 37% (25–51%) |
| 인플루엔자(계절기 변종) | 호흡기방울 | 1.3 (1.2–1.4)[49] | 23% (17–29%) |
| 안데스한타바이러스 | 호흡기 방울 및 체액 | 1.2 (0.8–1.6)[50] | 16% (0–36%)[c] |
| 니파바이러스 | 체액 | 0.5[51] | 0%[c] |
| 메르스 | 호흡기방울 | 0.5 (0.3–0.8)[52] | 0%[c] |
대중문화에서
가상의 의학 재해 스릴러인 2011년 영화 컨티멘션에서는 사례 연구에서 유행병으로 치명적인 바이러스 감염의 진행을 반영하기 위해 블로거의 R 에 대한 계산이 제시된다.묘사된 방법들은 결함이 있었다.[22]
참고 항목
- 역학에서 구획 모형
- E-epidemiology(전자 항생물학)
- Epi Info 소프트웨어 프로그램
- 역학법
- 역학전환
메모들
- ^ 를 사용하여 p=1− .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{으로 계산한다.border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1/R0.
- ^ a b 다른 출처에서 수정된 데이터가 있는 교육 코스의[33] 모듈로부터.[34][35][36]
- ^ a b c R0 < 1.0>하면 병은 자연히 사라진다.
- 역학의 구획 모델은 SIR 모델을 사용하는 취약(S), 감염(I) 및 회복(R) 인구의 시간에 따른 질병 역학을 설명한다.SIR 모델에서 ( ) 과 은(는) 서로 다른 수량이라는 점에 유의하십시오. 전자는 t = 0에서 복구된 횟수를 설명하는 반면 후자는 복구 빈도에 대한 접점 빈도 사이의 비율을 설명한다.
- 헬드 L, 닭이 N, 오닐 PD, Wallinga J(11월 7일 2019년).핸드 북 전염병 질병 자료 분석의.CRC프레스. p. 347. 아이 에스비엔 978-1-351-83932-7.광동 지방 질병 관리 본부에 따르면,"효과적인 생식 수(R또는 리 더 일반적으로 중등 경우[원문대로]전염성 사건마다 의해 생성된 평균적인 수치로 정의된다 전달률, 설명에 사용된다.".예를 들어, 현재 진행 중인 유행병 동안 한 번의 예비 추정치에 따르면, 사스-CoV-2의 유효 생식 수는 2.9인 반면 [citation needed]사스의 경우 1.77인 것으로 밝혀졌다.
참조
- ^ Milligan GN, Barrett AD (2015). Vaccinology : an essential guide. Chichester, West Sussex: Wiley Blackwell. p. 310. ISBN 978-1-118-63652-7. OCLC 881386962.
- ^ a b Fraser C, Donnelly CA, Cauchemez S, Hanage WP, Van Kerkhove MD, Hollingsworth TD, et al. (June 2009). "Pandemic potential of a strain of influenza A (H1N1): early findings". Science. 324 (5934): 1557–61. Bibcode:2009Sci...324.1557F. doi:10.1126/science.1176062. PMC 3735127. PMID 19433588.
- ^ a b Becker NG, Glass K, Barnes B, Caley P, Philp D, McCaw JM, et al. (April 2006). "The reproduction number". Using Mathematical Models to Assess Responses to an Outbreak of an Emerged Viral Respiratory Disease. National Centre for Epidemiology and Population Health. ISBN 1-74186-357-0. Retrieved February 1, 2020.
- ^ Adam D (July 2020). "A guide to R - the pandemic's misunderstood metric". Nature. 583 (7816): 346–348. Bibcode:2020Natur.583..346A. doi:10.1038/d41586-020-02009-w. PMID 32620883.
- ^ Jones J. "Notes On R0" (PDF). Stanford University.
- ^ Siegel E. "Why 'Exponential Growth' Is So Scary For The COVID-19 Coronavirus". Forbes. Retrieved March 19, 2020.
- ^ a b c d e Delamater PL, Street EJ, Leslie TF, Yang YT, Jacobsen KH (January 2019). "Complexity of the Basic Reproduction Number (R0)". Emerging Infectious Diseases. 25 (1): 1–4. doi:10.3201/eid2501.171901. PMC 6302597. PMID 30560777.
- ^ Fine, P.; Eames, K.; Heymann, D. L. (April 1, 2011). "'Herd Immunity': A Rough Guide". Clinical Infectious Diseases. 52 (7): 911–916. doi:10.1093/cid/cir007. PMID 21427399.
- ^ Smith DL, Battle KE, Hay SI, Barker CM, Scott TW, McKenzie FE (April 5, 2012). "Ross, macdonald, and a theory for the dynamics and control of mosquito-transmitted pathogens". PLOS Pathogens. 8 (4): e1002588. doi:10.1371/journal.ppat.1002588. PMC 3320609. PMID 22496640.
- ^ Macdonald G (September 1952). "The analysis of equilibrium in malaria". Tropical Diseases Bulletin. 49 (9): 813–29. PMID 12995455.
- ^ J.H. 존스, R.의0 노트.스탠퍼드 대학교(2007년).
- ^ a b Blower SM, McLean AR, Porco TC, Small PM, Hopewell PC, Sanchez MA, Moss AR (August 1995). "The intrinsic transmission dynamics of tuberculosis epidemics". Nature Medicine. 1 (8): 815–21. doi:10.1038/nm0895-815. PMID 7585186. S2CID 19795498.
- ^ Ma Y, Horsburgh CR, White LF, Jenkins HE (September 2018). "Quantifying TB transmission: a systematic review of reproduction number and serial interval estimates for tuberculosis". Epidemiology and Infection. 146 (12): 1478–1494. doi:10.1017/S0950268818001760. PMC 6092233. PMID 29970199.
- ^ Diekmann O, Heesterbeek JA, Metz JA (1990). "On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations". Journal of Mathematical Biology. 28 (4): 365–82. doi:10.1007/BF00178324. hdl:1874/8051. PMID 2117040. S2CID 22275430.
- ^ Wohl S, Schaffner SF, Sabeti PC (September 2016). "Genomic Analysis of Viral Outbreaks". Annual Review of Virology. 3 (1): 173–195. doi:10.1146/annurev-virology-110615-035747. PMC 5210220. PMID 27501264.
- ^ Lipsitch M, Cohen T, Cooper B, Robins JM, Ma S, James L, et al. (June 2003). "Transmission dynamics and control of severe acute respiratory syndrome". Science. 300 (5627): 1966–70. Bibcode:2003Sci...300.1966L. doi:10.1126/science.1086616. PMC 2760158. PMID 12766207.
- ^ Rihan, Fathalla A.; Anwar, M. Naim (2012). "Qualitative Analysis of Delayed SIR Epidemic Model with a Saturated Incidence Rate". International Journal of Differential Equations. 2012: 1–13. doi:10.1155/2012/408637.
- ^ Garnett GP (February 2005). "Role of herd immunity in determining the effect of vaccines against sexually transmitted disease". The Journal of Infectious Diseases. 191 (Suppl 1): S97-106. doi:10.1086/425271. PMID 15627236.
- ^ Rodpothong P, Auewarakul P (October 2012). "Viral evolution and transmission effectiveness". World Journal of Virology. 1 (5): 131–4. doi:10.5501/wjv.v1.i5.131. PMC 3782273. PMID 24175217.
- ^ Dabbaghian V, Mago VK (2013). Theories and Simulations of Complex Social Systems. Springer. pp. 134–35. ISBN 978-3642391491. Retrieved March 29, 2015.
- ^ a b Li J, Blakeley D, Smith RJ (2011). "The failure of R0". Computational and Mathematical Methods in Medicine. 2011 (527610): 527610. doi:10.1155/2011/527610. PMC 3157160. PMID 21860658.
- ^ a b Byrne M (October 6, 2014), "The Misunderstood Number That Predicts Epidemics", vice.com, retrieved March 23, 2020
- ^ Balkew TM (December 2010). The SIR Model When S(t) is a Multi-Exponential Function (Thesis). East Tennessee State University.
- ^ Ireland MW, ed. (1928). The Medical Department of the United States Army in the World War, vol. IX: Communicable and Other Diseases. Washington: U.S.: U.S. Government Printing Office. pp. 116–7.
- ^ Diekmann O, Heesterbeek JA (2000). "The Basic Reproduction Ratio". Mathematical Epidemiology of Infectious Diseases : Model Building, Analysis and Interpretation. New York: Wiley. pp. 73–98. ISBN 0-471-49241-8.
- ^ Chowell G, Hengartner NW, Castillo-Chavez C, Fenimore PW, Hyman JM (July 2004). "The basic reproductive number of Ebola and the effects of public health measures: the cases of Congo and Uganda". Journal of Theoretical Biology. 229 (1): 119–26. arXiv:q-bio/0503006. Bibcode:2004JThBi.229..119C. doi:10.1016/j.jtbi.2004.03.006. PMID 15178190. S2CID 7298792.
- ^ Ajelli M, Iannelli M, Manfredi P, Ciofi degli Atti ML (March 2008). "Basic mathematical models for the temporal dynamics of HAV in medium-endemicity Italian areas". Vaccine. 26 (13): 1697–707. doi:10.1016/j.vaccine.2007.12.058. PMID 18314231.
- ^ Heffernan JM, Smith RJ, Wahl LM (September 2005). "Perspectives on the basic reproductive ratio". Journal of the Royal Society, Interface. 2 (4): 281–93. doi:10.1098/rsif.2005.0042. PMC 1578275. PMID 16849186.
- ^ Guerra FM, Bolotin S, Lim G, Heffernan J, Deeks SL, Li Y, Crowcroft NS (December 2017). "The basic reproduction number (R0) of measles: a systematic review". The Lancet. Infectious Diseases. 17 (12): e420–e428. doi:10.1016/S1473-3099(17)30307-9. PMID 28757186.
- ^ Ireland's Health Services. Health Care Worker Information (PDF). Retrieved March 27, 2020.
- ^ 오스트레일리아 보건부 몰스 실험실 사례 정의(LCD)
- ^ "Omicron is the Dominant COVID Variant for Two Reasons". Vitals. December 28, 2021. Retrieved March 15, 2022.
- ^ Centers for Disease Control and Prevention; World Health Organization (2001). "History and epidemiology of global smallpox eradication". Smallpox: disease, prevention, and intervention (training course) (Presentation). Atlanta: Centers for Disease Control and Prevention (published August 25, 2014). cdc:27929. Archived (PDF) from the original on March 17, 2017. Retrieved June 17, 2021.
- ^ Fine, Paul E. M. (1993). "Herd Immunity: History, Theory, Practice". Epidemiologic Reviews. 15 (2): 265–302. doi:10.1093/oxfordjournals.epirev.a036121. PMID 8174658.
- ^ Luman, ET; Barker, LE; Simpson, DM; Rodewald, LE; Szilagyi, PG; Zhao, Z (May 2001). "National, state, and urban-area vaccination-coverage levels among children aged 19–35 months, United States, 1999". American Journal of Preventive Medicine. 20 (4): 88–153. doi:10.1016/s0749-3797(01)00274-4. PMID 12174806.
- ^ Jiles, RB; Fuchs, C; Klevens, RM (September 22, 2000). "Vaccination coverage among children enrolled in Head Start programs or day care facilities or entering school". Morbidity and Mortality Weekly Report. 49 (9): 27–38. PMID 11016876.
- ^ Kretzschmar M, Teunis PF, Pebody RG (June 2010). "Incidence and reproduction numbers of pertussis: estimates from serological and social contact data in five European countries". PLOS Medicine. 7 (6): e1000291. doi:10.1371/journal.pmed.1000291. PMC 2889930. PMID 20585374.
- ^ Liu, Ying; Rocklöv, Joacim (October 1, 2021). "The reproductive number of the Delta variant of SARS-CoV-2 is far higher compared to the ancestral SARS-CoV-2 virus". Journal of Travel Medicine. 28 (7). doi:10.1093/jtm/taab124. ISSN 1708-8305. PMC 8436367. PMID 34369565.
- ^ Gani R, Leach S (December 2001). "Transmission potential of smallpox in contemporary populations". Nature. 414 (6865): 748–51. Bibcode:2001Natur.414..748G. doi:10.1038/414748a. PMID 11742399. S2CID 52799168. Retrieved March 18, 2020.
- ^ Gallagher, James (June 12, 2021). "Covid: Is there a limit to how much worse variants can get?". BBC News. Retrieved July 21, 2021.
- ^ "Playing the Numbers Game: R0". National Emerging Special Pathogen Training and Education Center. Archived from the original on May 12, 202. Retrieved December 27, 2020.
[...] while infections that require sexual contact like HIV have a lower R0 (2-5).
- ^ Prather, Kimberly A.; Marr, Linsey C.; Schooley, Robert T.; McDiarmid, Melissa A.; Wilson, Mary E.; Milton, Donald K. (October 16, 2020). "Airborne transmission of SARS-CoV-2". Science. 370 (6514): 303.2–304. Bibcode:2020Sci...370..303P. doi:10.1126/science.abf0521. PMID 33020250. S2CID 222145689.
- ^ Billah, Arif; Miah, Mamun; Khan, Nuruzzaman (November 11, 2020). "Reproductive number of coronavirus: A systematic review and meta-analysis based on global level evidence". PLOS ONE. 15 (11): e0242128. Bibcode:2020PLoSO..1542128B. doi:10.1371/journal.pone.0242128. PMC 7657547. PMID 33175914.
- ^ Consensus document on the epidemiology of severe acute respiratory syndrome (SARS). Department of Communicable Disease Surveillance and Response (Technical report). World Health Organization. p. 26. hdl:10665/70863. WHO/CDS/CSR/GAR/2003.11.
A number of researchers have estimated the basic reproduction number by fitting models to the initial growth of epidemics in a number of countries. Their observations indicate that the SARS-CoV is less transmissible than initially thought with estimates of Ro in the range of 2-4.
- ^ Truelove SA, Keegan LT, Moss WJ, Chaisson LH, Macher E, Azman AS, Lessler J (June 2020). "Clinical and Epidemiological Aspects of Diphtheria: A Systematic Review and Pooled Analysis". Clinical Infectious Diseases. 71 (1): 89–97. doi:10.1093/cid/ciz808. PMC 7312233. PMID 31425581.
- ^ Freeman C. "Magic formula that will determine whether Ebola is beaten". The Telegraph. Telegraph.Co.Uk. Archived from the original on January 12, 2022. Retrieved March 30, 2020.
- ^ "Omicron transmission: how contagious diseases spread". Nebraska Medicine. December 21, 2021. Retrieved January 25, 2022.
- ^ Wong ZS, Bui CM, Chughtai AA, Macintyre CR (April 2017). "A systematic review of early modelling studies of Ebola virus disease in West Africa". Epidemiology and Infection. 145 (6): 1069–1094. doi:10.1017/S0950268817000164. PMID 28166851.
The median of the R0 mean estimate for the ongoing epidemic (overall) is 1.78 (interquartile range: 1.44, 1.80)
- ^ Chowell G, Miller MA, Viboud C (June 2008). "Seasonal influenza in the United States, France, and Australia: transmission and prospects for control". Epidemiology and Infection. Cambridge University Press. 136 (6): 852–64. doi:10.1017/S0950268807009144. PMC 2680121. PMID 17634159.
The reproduction number across influenza seasons and countries lied in the range 0.9–2.0 with an overall mean of 1.3, and 95% confidence interval (CI) 1.2–1.4.
- ^ Martínez, Valeria P.; Di Paola, Nicholas; Alonso, Daniel O.; Pérez-Sautu, Unai; Bellomo, Carla M.; Iglesias, Ayelén A.; et al. (December 3, 2020). "'Super-Spreaders' and Person-to-Person Transmission of Andes Virus in Argentina". New England Journal of Medicine. 383 (23): 2230–2241. doi:10.1056/NEJMoa2009040. PMID 33264545. S2CID 227259435.
- ^ Luby SP (October 2013). "The pandemic potential of Nipah virus". Antiviral Research. 100 (1): 38–43. doi:10.1016/j.antiviral.2013.07.011. PMID 23911335.
- ^ Kucharski AJ, Althaus CL (June 2015). "The role of superspreading in Middle East respiratory syndrome coronavirus (MERS-CoV) transmission". Euro Surveillance. 20 (25): 14–8. doi:10.2807/1560-7917.ES2015.20.25.21167. PMID 26132768.
추가 읽기
| 스콜리아는 기본 재생산 번호(Q901464)에 대한 프로필을 가지고 있다. |
- Heesterbeek, J.A.P. (2002). "A brief history of R0 and a recipe for its calculation". Acta Biotheoretica. 50 (3): 189–204. doi:10.1023/a:1016599411804. hdl:1874/383700. PMID 12211331. S2CID 10178944.
- Heffernan, J.M; Smith, R.J; Wahl, L.M (September 22, 2005). "Perspectives on the basic reproductive ratio". Journal of the Royal Society Interface. 2 (4): 281–293. doi:10.1098/rsif.2005.0042. PMC 1578275. PMID 16849186.
- Jones JH (May 1, 2007). "Notes on " (PDF). Retrieved November 6, 2018.
- Van Den Driessche, P.; Watmough, James (2008). "Further Notes on the Basic Reproduction Number". Mathematical Epidemiology. Lecture Notes in Mathematics. Vol. 1945. pp. 159–178. doi:10.1007/978-3-540-78911-6_6. ISBN 978-3-540-78910-9.










 전염성, 즉 접촉에 의해 감염될 확률이다.또한 (동물이 흔히 그렇듯이) 감염 개인을 발견하여 격리, 치료 또는 제거함으로써
전염성, 즉 접촉에 의해 감염될 확률이다.또한 (동물이 흔히 그렇듯이) 감염 개인을 발견하여 격리, 치료 또는 제거함으로써



 걸쳐 진단된 감염
걸쳐 진단된 감염 


 같이
같이 















 잠재 감염 개체 수
잠재 감염 개체 수 














