응력을 받는 재료 변형을 설명하기 위한 수학적 모델
연속체 역학 에서 유한 변형 이론 (큰 변형 이론 또는 큰 변형 이론이라고 도 함)은 변형 및/또는 회전이 무한 변형 이론에 내재된 가정을 무효화하기에 충분히 큰 변형과 함께 취급 한다.이 경우, 연속체의 미형식과 변형 구성은 크게 다르며, 그 사이에 명확한 구별이 필요합니다. 이는 일반적으로 탄성체 , 탄성 변형 물질 및 기타 유체 및 생물학적 연조직 의 경우입니다.
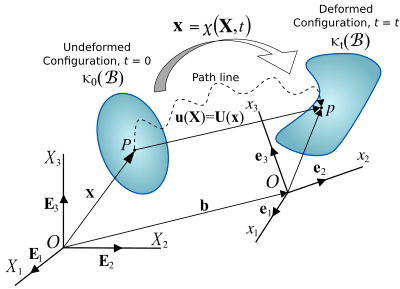
변위 물체의 변위는 강체 변위와 변형이라는 두 가지 요소로 구성됩니다.
강체 변위는 모양이나 크기를 변경하지 않고 동시에 변환(물리학) 및 차체의 회전으로 구성됩니다. 변형은 초기 또는 미형식 구성 0 0 )(\displaystyle \kappa {0}({\mathcal {B})) t ( B )(\displaystyle \kappa {t}({\mathcal {B})) 연속체의 구성 변화는 변위 필드에 의해 설명될 수 있다. 변위장 은 체내의 모든 입자에 대한 모든 변위 벡터의 벡터장 으로, 변형된 구성과 변형되지 않은 구성을 관련짓습니다.두 입자 사이의 거리는 변형이 발생한 경우에만 변경됩니다. 변형이 없는 변위는 강체 변위입니다.
재료 좌표(라그랑주 설명) 변수 i에 의해 지수화된 입자의 변위는 다음과 같이 표현될 수 있다.미형성 구성 Pi (\ displaystyle P_{i 구성 pi (\ displaystyle p_{i 변위 벡터라고 합니다. 좌표계 (\ displaystyle p_{i 대신 X}) x displaystyle \mathbf }) 사용 하여 라그랑스 변위 설명을 얻었다 .ctor:
u ( X , t ) = u i e i \displaystyle \mathbf {u}(\mathbf {X},t)=u_{i}\mathbf {e}_{i}) 여기 \ displaystyle \mathbf {e} {i} 기초 를 정의하는 직교 정규 단위 벡터입니다.
재료 좌표, 즉 (\ displaystyle \mathbf X
u ( X , t ) = b ( t ) + x ( X , t ) − X 또는 u i = α i J b J + x i − α i J X J \displaystyle \mathbf {u}(\mathbf {X},t)=\mathbf {b}(t)+\mathbf {x}(\mathbf {X}-\mathbf {X})\qquad {i}=\alpha _iJB}{x} J}+x_{i}-\alpha _{iJ}X_{ J}} 여기 t displaystyle \mathbf {b}(t)}
재료 좌표에 대한 변위 벡터의 편도함수 는 재료 변위 경사 텐서 x X displaystyle \nabla {\mathbf {X} }\mathbf {u} \,\!}
∇ X u = ∇ X x − R = F − R 또는 ∂ u i ∂ X K = ∂ x i ∂ X K − α i K = F i K − α i K \displaystyle \mathbf {X} =\mathbf {X} -\mathbf {R} =\mathbf {F} -\mathbf {R} \qquad ufrac} 여기 displaystyle \mathbf {F}} 변형 경사
공간 좌표(을레리아어 설명) 오일러식 설명 에서는 미형성 구성의 입자 displaystyle ) 변위 벡터라고 합니다.
U ( x , t ) = U J E J \displaystyle \mathbf {U}(\mathbf {x},t)= U_{J}\mathbf {E}_{J} 여기 displaystyle \mathbf {E} _{i}
공간 좌표로 표현됩니다. x {\ displaystyle \mathbf {x displaystyle \mathbf {U}}
U ( x , t ) = b ( t ) + x − X ( x , t ) 또는 U J = b J + α J i x i − X J \displaystyle \mathbf {U}(\mathbf {x},t)=\mathbf {b}(t)+\mathbf {x} -\mathbf {X}(\mathbf {x},t)\qquad U_{J}={J+}\alpha}_i} _mathbf {x}
공간 좌표에 대한 변위 벡터의 편도함수는 공간 변위 구배 텐서 δ U displaystyle \nabla {\mathbf {x} }\mathbf {U} \,\!}
∇ x U = R T − ∇ x X = R T − F − 1 또는 ∂ U J ∂ x k = α J k − ∂ X J ∂ x k = α J k − F J k − 1 . \displaystyle \mathbf {x} \mathbf {U} =\mathbf {R} ^{T}-\nabla _{\mathbf {X} =\mathbf {R} ^{T}-\mathbf {F} =\q} ^-{text} }
재료 좌표계와 공간 좌표계 사이의 관계 α Ji (\ displaystyle \alpha {Ji}) 벡터 E (\ displaystyle \mathbf {E}_{J}) e (\displaystyle \mathbf {e}_{i 방향 코사인 것이다.따라서
E J ⋅ e i = α J i = α i J \displaystyle \mathbf {E}_{J}\cdot \mathbf {e}_{i}=\alpha _{Ji}=\alpha _{iJ}}
다음 ui UJ의 관계 .
u i = α i J U J 또는 U J = α J i u i \displaystyle u_{i}=\alpha_{iJ}U_{J}\qquad\text{or}\qquad U_{J}=\alpha_{Ji}u_{i}
알고 있으니까
e i = α i J E J \displaystyle \mathbf {e} _{i}=\alpha _{iJ}\mathbf {E} _{J} 그리고나서 u ( X , t ) = u i e i = u i ( α i J E J ) = U J E J = U ( x , t ) \displaystyle \mathbf {u}(\mathbf {X},t)=u_{i}\mathbf {e}_{i}=u_{i}(\alpha_{iJ}\mathbf {E}_{J}) =U_{J}\mathbf {E}_{J}=\mathbf {U}(\mathbf {x},t)}
변형 및 변형되지 않은 구성의 좌표계 결합 변형 = 0 되고 크로네커 델타 가 됩니다.
E J ⋅ e i = δ J i = δ i J \displaystyle \mathbf {E}_{J}\cdot \mathbf {e}_{i}=\delta _{iJ}
따라서 재료(미형식) 좌표에서 변위는 다음과 같이 표현될 수 있다.
u ( X , t ) = x ( X , t ) − X 또는 u i = x i − δ i J X J \displaystyle \mathbf {u}(\mathbf {X},t)=\mathbf {x}(\mathbf {X},t)-\mathbf {X}\qquad u_{i}=x_{i}-\mathbf {iJ}X}_{x}_{x}) J}}
공간(변형) 좌표에서 변위는 다음과 같이 표현될 수 있습니다.
U ( x , t ) = x − X ( x , t ) 또는 U J = δ J i x i − X J {\displaystyle \mathbf {U}(\mathbf {x},t)=\mathbf {x} -\mathbf {X}(\mathbf {x},t)\qquad U_{J}=\delta _{Ji}x_{i}-X_{J}}}}}
변형 경사 텐서 변형구배 텐서 X t = F j K e i K displaystyle \mathbf {F}(\mathbf {X} F_{jK}\mathbf {e}_{j}\otimes\mathbf {I}_{K} displaystyle \mathbf {e} _ j} _K displaystyle \mathbf {I}_{K\} \}}) 2개
δ X t displaystyle \chi mathbf X } 연속성 displaystyle mathbf H } = 1 displaystyle \mathbf { F ^ 1 . 여기 그런 다음, 암묵적 함수 [1] 야코비안 행렬식 X , t ) displaystyle mathbf },t 비음정칙적 이어야 한다. 즉, X ,t ) = det (X ,t ) 0 displaystyle mathbf },t \detf)
재료 변형 구배 텐서 X t = F j K i I displaystyle mathbf { F } mathbf = F_{jK}\mathbf {e}_{j}\otimes \mathbf {I}_{K}} 매핑 함수 또는 함수 관계 X , t )\displaystyle \chi(\mathbf {X}, t 구배 를 나타내는 2차 텐서이다.재료 변형 구배 텐서는 위치 (\displaystyle mathbf \,\!}) 선형 변환)하여 국소 변형을 특성화합니다. 변형 , (\ displaystyle \ci(\mathbf {X},t 연속성 , 즉 X(\displaystyle \mathbf {X}) 시간 displaystyle ,\!}) 않음 을 의미합니다.이렇게 해서
d x = ∂ x ∂ X d X 또는 d x j = ∂ x j ∂ X K d X K = ∇ χ ( X , t ) d X 또는 d x j = F j K d X K . = F ( X , t ) d X {\displaystyle {displaystyle}d\mathbf {x} &=displayfrac {\displaystyle \mathbf {X}}},d\mathbf {X} \qquad & {\text{or} =dx_{j} =displayfrac {x_d} F_{jK}, dX_{K}, \\&=\mathbf {F}(\mathbf {X},t),d\mathbf {X} \end{aligned}})
상대 변위 벡터 위치 벡터 = X I displaystyle \mathbf {X} X_{ 또는 재료 점 P displaystyle } I}\mathbf {I}_ {I}: 본체의 변위 후, 새로운 구성에서 displaystyle 나타나는 위치 = x i i displaystyle mathbf { x x _ mathbf e _ i } 불편함
이제 위치 벡터 δ = X I δ X I displaystyle \mathbf {X} +\Delta \mathbf { X_{ 점 displaystyle displaystyle ,\!} I}+\Delta X_{I}\mathbf {I}_{I 벡터 δ displaystyle \mathbf {x} +\Delta \mathbf {x} \!} 가정합니다. f {x}은 ( 입자 displaystyle ) (\displaystyle ) X (\ displaystyle \mathbf {X}) d displaystyle \mathbf {x
x + d x = X + d X + u ( X + d X ) d x = X − x + d X + u ( X + d X ) = d X + u ( X + d X ) − u ( X ) = d X + d u {\displaystyle{\begin{정렬}\mathbf{)}+d\mathbf{)}&=\mathbf{X}+d\mathbf{X}+\mathbf{u}(\mathbf{X}+d\mathbf{X})\\d\mathbf{)}&=\mathbf{X}-\mathbf{)}+d\mathbf{X}+\mathbf{u}(\mathbf{X}+d\mathbf{X})\\&, =d\mathbf{X}+\mathbf{u}(\mathbf{X}+d\mathbf{X})-\mathbf{u}(\mathbf{X})\\&, =d\mathbf{X}+d\mathbf.{u}\\\end{alig ned}}}
여기 {\ displaystyle \mathbf {du} 변위 벡터이며, 변형 구성에서 displaystyle displaystyle 상대 변위를 나타냅니다.
테일러 근사 극소수 (\ displaystyle \mathbf {X displaystyle ,\!} 중심으로 Taylor 급수 확장을 사용하여 인접한 특정 변위 벡터의 성분을 근사할 수 있습니다.le (표시 스타일 )
u ( X + d X ) = u ( X ) + d u 또는 u i ∗ = u i + d u i ≈ u ( X ) + ∇ X u ⋅ d X 또는 u i ∗ ≈ u i + ∂ u i ∂ X J d X J . {\displaystyle{\begin{정렬}\mathbf{u}(\mathbf{X}+d\mathbf{X})&, =\mathbf{u}(\mathbf{X})+d\mathbf{u}\quad&{\text{또는}}&\quad u_{나는}^{*}=u_{나는}+du_{나는}\\&, \approx \mathbf{u}(\mathbf{X})+\nabla _{\mathbf{X}}\mathbf{u}\cdot d\mathbf{X}\quad&{\text{또는}}&\quad u_{나는}^{*}\approx u_{나는}+{\frac{\partial u_{나는}}{\pa.rtial X_{J}}}dX_{J}\,. \end { aligned}} 따라서 앞의 방정식 d = d X d displaystyle \mathbf {x} = d\mathbf {X} d\mathbf {u} d x = d X + d u = d X + ∇ X u ⋅ d X = ( I + ∇ X u ) d X = F d X {\displaystyle {cdot d\mathbf {x} &=d\mathbf {X} +\mathbf {u} \&=d\mathbf {X} +\mathbf {u} \cdot d\mathbf {X} +\mathbf {x} \\mathbf {xi}
변형 구배 시간파생성 물체의 시간 의존적 변형을 수반하는 계산은 종종 변형 구배의 시간 도함수를 계산해야 한다. 이러한 도함수의 기하학적으로 일관된 정의를 위해서는 미분 [2] 기하학 으로의 이동이 필요하지만, 이 기사에서는 이러한 문제를 피한다.
F(\ displaystyle\mathbf {F})
F ˙ = ∂ F ∂ t = ∂ ∂ t [ ∂ x ( X , t ) ∂ X ] = ∂ ∂ X [ ∂ x ( X , t ) ∂ t ] = ∂ ∂ X [ V ( X , t ) ] ({displaystyle {dot {mathbf {F}}=frac {\frac t}}=frac {\frac t}\left[\frac \mathbf {X},t}{\frac \mathbf {X}})=frac 오른쪽 }}\left[\mathbf {V}(\mathbf {X},t)\right]} 여기 (\ displaystyle \mathbf {V}) 오른쪽에 있는 도함수는 재료 속도 구배를 나타냅니다. 도함수에 대한 연쇄 규칙을 적용하여 이를 공간 구배로 변환하는 것이 일반적이다. F ˙ = ∂ ∂ X [ V ( X , t ) ] = ∂ ∂ X [ v ( x ( X , t ) , t ) ] = ∂ ∂ x [ v ( x , t ) ] x = x ( X , t ) ⋅ ∂ x ( X , t ) ∂ X = l ⋅ F (\displaystyle {\dot \mathbf {F}} = flac {\mathbf {X} } } \ left [ \ mathbf { V } ( \ mathbf { X } , t ) \ right ] = frac { \ dot \ mathbf { X } { X } } } } } } } } } \ [ \ \ [ \ [ \ mathbf v ] \frac {\mathbf {x}}\left[\mathbf {v}(\mathbf {x},t)\right]_{\mathbf {x} =\mathbf {x}(\mathbf {X},t)}\cdot {\frac {\mathbf} 여기 displaystyle {l}} 공간 속도 구배이며, 여기 x , = V X t displaystyle \mathbf {x} = mathbf {V} mathbf {X } t) ) tial velocity gradient는 시간에 일정하다, 위의 방정식은 정확하게 풀 수 있다. F = e l t \displaystyle \mathbf {F} = e^{\boldsymbol {l}},t} F = 1 displaystyle \mathbf {F} mathbf {1} } 가정 = 0 displaystyle =0 위의 지수 를 계산하는 방법에는 여러 가지가 있습니다.
연속체 역학에 자주 사용되는 관련 수량은 각각 다음과 같이 정의된 변형 텐서 와 스핀 텐서이다.
d = 1 2 ( l + l T ) , w = 1 2 ( l − l T ) . {\displaystyle {\boldsymbol {d}}=bladtfrac {1}{2}}\leftsymbol {l}+{\boldsymbol {l}^{ T}\오른쪽),~{\boldsymbol {w}}=tfrac {1}{2}}\leftboldsymbol {l}-{\boldsymbol {l}^{ T}\right), } 변형 텐서는 선 요소의 신장 속도를 제공하는 반면 스핀 텐서는 운동의 회전 속도 또는 소용돌이도 를 나타냅니다.
변형 구배 역의 재료 시간 도함수(기준 구성 고정 유지)는 유한 변형과 관련된 분석에서 종종 필요하다. 이 파생상품은
∂ ∂ t ( F − 1 ) = − F − 1 ⋅ F ˙ ⋅ F − 1 . {\displaystyle {\frac } \left(\mathbf {F} ^{-1}\cdot {\mathbf {F}}}\cdot \mathbf {F} ^-1}, } 위의 관계는 F 1 µ x = d X displaystyle \mathbf {F} 1}\cdot \mathbf {x} \mathbf {X }} = {\style dot\mathbf }}}}} 재료
표면 및 볼륨 요소의 변환 변형 구성의 영역과 관련하여 정의된 수량을 기준 구성의 영역과 관련된 수량과 변환하기 위해 다음과 같이 Nanson의 관계를 사용한다.
d a n = J d A F − T ⋅ N {\displaystyle da~\mathbf {n} =J~dA~\mathbf {F} ^{-T}\cdot \mathbf {N} } 여기 displaystyle ) d displaystyle ) 영역, n(\ mathbf }) (\ displaystyle \mathbf {N}) 기준 구성에서 normal F {\displaystyle mathbf {F} J = det displaystyle det \mathbf {F} ,\!}
볼륨 요소의 변환 공식은 다음과 같습니다.
d v = J d V {\displaystyle dv=J~dV}
변형구배텐서의 극분해 변형구배 displaystyle \mathbf {F} \,\!} 극분해 정리를 사용하여 직교 텐서와 양의 2차 텐서(Truesdell 및 Noll, 1965)의 곱으로 분해할 수 있다.
F = R U = V R {\displaystyle \mathbf {F} =\mathbf {R} \mathbf {U} =\mathbf {V} \mathbf {R} } 여기서 텐서 displaystyle \mathbf R}) 적절한 직교 텐서입니다. 즉, R = R T mathbf {R} ^{T} 및 det = 1 det \mathbf {R} 1! Sor ; 및 V {\displaystyle mathbf } } 왼쪽 텐서.오른쪽 과 왼쪽이라는 용어 는 각각 회전 텐서 .\displaystyle mathbf \,\!} U{\displaystyle \mathbf{U}}과 V{\displaystyle \mathbf{V}}둘 다 긍정적인 확실한, 즉)⋅ U⋅)>0{\displaystyle \mathbf{)}\cdot\mathbf{U}\cdot \mathbf{)}>0}일 경우, 탭 ⋅ V⋅)>0{\displaystyle \mathbf{)}\cdot\mathbf{V}\cdot \mathbf{)}>0}일 경우에 대한 모든 0이 아니x. ∈ R3 \displaystyle \mathbf {x} in \mathbb {R} 3 대칭 텐서 . U = U T displaystyle mathbf mathbf ^{T V = V T displaystyle \mathbf {V} mathbf {V} T
이 분해는 미형성 구성의 라인 요소 d (\ displaystyle \ mathbf { X}) d x (\ displaystyle x }) 변형 즉 d x = F displaystyle d mathbf {x}). 요소를 U displaystyle \mathbf {U 즉 dx = U d displaystyle \mathbf {U}, \ mathbf {X},\!} R . ; 또는 이와 동등하게 먼저 강성 회전 (\ displaystyle \mathbf {R}) 예 ′ = R d X displaystyle \mathbf {x} mathbf {R} d\mathbf ,\!) 스트레칭 mathbf 적용 {V} ,d\mathbf {x} }
R {\ displaystyle \mathbf {R}
V = R ⋅ U ⋅ R T \displaystyle \mathbf {V} =\mathbf {R} \cdot \mathbf {U} \cdot \mathbf {R} ^{T} 따라서 (\ displaystyle \mathbf {U}) (\ displaystyle \mathbf {V}) 고유값이나 주연장 은 같지만 고유 벡터 또는 주방향 Ni (\ displaystyle \mathbf N }_ {i }) ni (\displaystyle \mathbf n}_i},\!) . 주요 방향은 다음과 같습니다. n i = R N i . \displaystyle \mathbf {n} _{i}=\mathbf {R} \mathbf {N} _{i}. }
F(\ displaystyle \mathbf {F} }) 독특 특이값 분해 의 결과이다.
변형 텐서 기계학에는 몇 가지 회전비의존 변형 텐서가 사용됩니다. 고체역학에서 가장 인기 있는 것은 오른쪽과 왼쪽의 코시-녹색 변형 텐서입니다.
순수한 회전은 변형 가능한 물체에 어떠한 변형도 유발하지 않기 때문에 연속체 역학 에서 회전의존적인 변형 측정을 사용하는 것이 종종 편리하다. 회전 후 역회전하면 변화가 없기 때문에(R T = R T = I {\ displaystyle \mathbf {R} mathbf {R} ^{T R} ^{ =\mathbf { } ).
오른쪽 코시-녹색 변형 텐서 1839년 조지 그린 은 다음 과 [4] [5] 코시-녹색 변형 텐서 또는 그린의 변형 텐서로 알려진 변형 텐서를 도입했다.
C = F T F = U 2 또는 C I J = F k I F k J = ∂ x k ∂ X I ∂ x k ∂ X J . {\displaystyle \mathbf {C} =\mathbf {F} =\mathbf {U} ^{2}\qquad {text{or}}\qquad C_{ IJ}=F_{k I}~F_{kJ}=black {\flac x_{k}}{\flac X_{ I}} {\frac {\partial x_{k}} {\partial X_{J}}} }
물리적으로 코시-그린 텐서는 변형으로 인한 거리의 국소적 변화의 제곱을 제공 d 2 = d X x displaystyle \mathbf {x} ^{2 d\mathbf {X} cdot \mathbf {C} cdot \mathbf C}
변형률 에너지 밀도 함수 의 식에는 C(\ displaystyle \mathbf {C}) 가장 일반적으로 사용되는 불변량 은 다음과 같습니다.
I 1 C := tr ( C ) = C I I = λ 1 2 + λ 2 2 + λ 3 2 I 2 C := 1 2 [ ( tr C ) 2 − tr ( C 2 ) ] = 1 2 [ ( C J J ) 2 − C I K C K I ] = λ 1 2 λ 2 2 + λ 2 2 λ 3 2 + λ 3 2 λ 1 2 I 3 C := 멈추다 ( C ) = J 2 = λ 1 2 λ 2 2 λ 3 2 . 디스플레이 스타일 I_{1}^{C}&:=captext{tr}(\mathbf {C})=C_{ II}=\lambda_{1}^{2}+\lambda_{2}+\lambda_{2}\ I_{2}^{C}&:=httfrac {1}{2}\left[({\text{tr}~\mathbf {C})^{2}-{\text{tr}(\mathbf {C}^{2}\right]=httfrac {1}{2}\left[C_{J}^{2}}^{2}^left[(\left[C})] IK}C_{KI}\right]=\lambda_{1}^2}\lambda_{2}_{2}+\lambda_{2}_{3}^{2}\lambda_{1}^2}\lambda_{2}\lambda_{2}\lambda_{2}\lambda_{2}\lambda_{2}\lambda_{1}{1}^{2}\lambda_{2}\rongbda_{1}^{2}\ I_{3}^{C}&:=\det(\mathbf {C})=J^{2}=\lambda_{1}^2}\lambda_{2}\lambda_{2}\lambda_{3}^2}. \end { aligned}} 여기 = det displaystyle :=\ mathbf }} 구배 displaystyle \mathbf {F}} i displaystyle \detda {i 일반적으로 좌표계의 3축과 정렬되지 않음).
핑거 변형 텐서 IUPAC 는 오른쪽 Cauchy-Green 변형 텐서(이 문서에서는 Cauchy 텐서라고 함)의 역수 1 (\displaystyle \mathbf } ^{-1 핑거 텐서 라고 부를 것을 권장합니다[5] 그러나 그 명명법은 응용역학에서 보편적으로 받아들여지지 않는다.
f = C − 1 = F − 1 F − T 또는 f I J = ∂ X I ∂ x k ∂ X J ∂ x k {\displaystyle \mathbf {f} =\mathbf {C} =\mathbf {F} ^{-1}\mathbf {F} ^{-T}\qquad {text{or}}}\qquad f_{} IJ = frac ( x x_ X ) I}} {\partial x_{k}} {\frac {\partial x_{J}} {\partial x_{k}}}
왼쪽 Cauchy-Green 또는 핑거 변형 텐서 오른쪽 그린-코시 변형 텐서에 대한 공식의 곱셈 순서를 바꾸면 다음과 같이 정의되는 왼쪽 코시-녹색 변형 텐서로 이어진다.
B = F F T = V 2 또는 B i j = ∂ x i ∂ X K ∂ x j ∂ X K {\displaystyle \mathbf {B} =\mathbf {F} ^{T} =\mathbf {V} ^{2} qquad {text{or} = bqquad B_{ij} = frac {\mathbf {F} } {f {f} }
왼쪽 코시-녹색 변형 텐서는 종종 요제프 핑거의 이름 을 딴 핑거 변형 텐서로 불린다 .[5] [6] [7]
변형률 에너지 밀도 함수 의 식에는 B(\ displaystyle \mathbf {B}) 일반적인 불변량은 다음과 같이 정의된다.
I 1 := tr ( B ) = B i i = λ 1 2 + λ 2 2 + λ 3 2 I 2 := 1 2 [ ( tr B ) 2 − tr ( B 2 ) ] = 1 2 ( B i i 2 − B j k B k j ) = λ 1 2 λ 2 2 + λ 2 2 λ 3 2 + λ 3 2 λ 1 2 I 3 := 멈추다 B = J 2 = λ 1 2 λ 2 2 λ 3 2 디스플레이 스타일 I_{1}&:=paramtext{tr}(\mathbf {B})=B_{i}=\lambda_{1}^2}+\parambda_{2}+\parambda_{3}^2}\\\\parambda_{i} I_{2}&:=httfrac {1}{2}}\left[(\text{tr}~\mathbf {B})^{2}-{\text{tr}(\mathbf {B})\right]=httfrac {1}{2}\left(B_ii}^{B}_K}_{K}) I_{3}&:=\det \mathbf {B} = J^{2}=\lambda _{1}^{2}\lambda _{2}\lambda _{2}\lambda _{3}^2}\end{aligned}} 여기 = det display det \mathbf {F}}
압축 가능한 재료의 경우 다음과 같이 약간 다른 불변량 세트가 사용됩니다.
( I ¯ 1 := J − 2 / 3 I 1 ; I ¯ 2 := J − 4 / 3 I 2 ; J ≠ 1 ) . {\displaystyle({\bar {I}}_{1}): =J^{-2/3} I_{1}~;~{\bar {I}}_{2}: =J^{-4/3} I_{2}~;~~J\neq 1)~.}
코시 변형 텐서 앞서 1828년 [8] 루이 코시 는 왼쪽 코시-녹색 변형 텐서 1 displaystyle \mathbf {B} 1 피올라 [5] 핑거 [9] 불린다 .
c = B − 1 = F − T F − 1 또는 c i j = ∂ X K ∂ x i ∂ X K ∂ x j {\displaystyle \mathbf {c} =\mathbf {B} ^{-1} ^{-T}\mathbf {F} ^{-1} \qquad {text{or} =qquad c_{ij} = partial_frac {-1}
스펙트럼 표현 3개의 주연장이 있는 , (\displaystyle lambda {i },\!) (\ mathbf {B}) 스펙트럼 분해 는 다음과 같다.
C = ∑ i = 1 3 λ i 2 N i ⊗ N i 그리고. B = ∑ i = 1 3 λ i 2 n i ⊗ n i {\displaystyle \mathbf {C} =\sum _{i=1}^{3}\sumda _{i}^{2}\mathbf {N}_{i}\otimes \mathbf {N}_{i}\qquad \mathbf {B} =_{i}^3}_sum {n}
더 나아가,
U = ∑ i = 1 3 λ i N i ⊗ N i ; V = ∑ i = 1 3 λ i n i ⊗ n i \displaystyle \mathbf {U} = \sum _{i=1}^{3}\sumda _{i} \mathbf {N} _{i} \otimes \mathbf {N} _{i} ~ ~\mathbf {V} =\sum _i=1}^{3}\da {i} _mathbf} _n} R = ∑ i = 1 3 n i ⊗ N i ; F = ∑ i = 1 3 λ i n i ⊗ N i \displaystyle \mathbf {R} =\sum _{i=1}^{3}\mathbf {n} _{i}~\mathbf {F} =\sum _{i=1}^{3}\mathbf {i} \mathbf {n} \mathbf {n} \mathbimes
주의하세요
V = R U R T = ∑ i = 1 3 λ i R ( N i ⊗ N i ) R T = ∑ i = 1 3 λ i ( R N i ) ⊗ ( R N i ) ({displaystyle \mathbf {V} =\mathbf {R} ~\mathbf {U} ~\mathbf {R} ^{T}=\sum _{i} ~\mathbf {R} ~\mathbf {N} \mathbf {F}) _{i} ) 따라서 스펙트럼 분해의 고유성은 n = R i displaystyle \mathbf {n} _{ mathbf {R} ~\mathbf {N} _{i Vdisplaystyle \mathbf {V} \,\!}) 공간적 스트레치 (spative right tensor)라고도 불린다. {U} \,\!} 재료 스트레치 텐서라고 합니다.
F( displaystyle \mathbf F}) Ni (\ displaystyle \mathbf {N } _ { i }) 작용 θ (\ displaystyle \lambda {i}) 방향
F N i = λ i ( R N i ) = λ i n i \displaystyle \mathbf {F} ~\mathbf {N} ~\mathbf {R} ~\mathbf {N} =\mathbf {n} ~\mathbf {n} _{i} 비슷한 맥락에서, F − T N i = 1 λ i n i ; F T n i = λ i N i ; F − 1 n i = 1 λ i N i . {\displaystyle \mathbf {F}^{-T}~\mathbf {N}_{i}~\mathbf {n}_{i}~\mathbf {F}^{T}~\mathbf {n}_{i}~{i}_mathbf {n}_mathbf}_mathbf {n}_mathbf {i}_{i}_{i}_mathbf}_mathbf}_mathbf {F}_{i}_{T}_mathb}
예 비압축성 재료의 일축 연장 α = α displaystyle \mathbf alpha alpha _{1 \,!} 스트레치비 α 1 α 2 α = 1 displaystyle \mathbf {1\alpha {\ {\} 2} alpha 알파 또는 α = α displaystyle \mathbf = alpha alpha 0 5 F = [ α 0 0 0 α − 0.5 0 0 0 α − 0.5 ] {\displaystyle \mathbf {F} = bb { bmatrix } \ 0 & \ alpha ^ { - 0 . 5 } \ \ 0 & \ alpha ^ { - 0 . 5 } \ \ end { bmatrix } } B = C = [ α 2 0 0 0 α − 1 0 0 0 α − 1 ] {\displaystyle \mathbf {B} =\mathbf {C} = begin{ { bmatrix ^ {2} & 0 \ \ 0 & \ alpha ^ { - 1 } \ \ \ \ 0 & 0 & \ alpha ^ { - 1 } 단순 전단 F = [ 1 γ 0 0 1 0 0 0 1 ] {\displaystyle \mathbf {F} = {b { bmatrix }1 & \ 0 & 1 \ 0 & 1 \ end { bmatrix } B = [ 1 + γ 2 γ 0 γ 1 0 0 0 1 ] {\displaystyle \mathbf {B} =\display {bmatrix}1+\display ^{2}&\display & 0&1\end {bmatrix}} C = [ 1 γ 0 γ 1 + γ 2 0 0 0 1 ] {\displaystyle \mathbf {C} = beginstyle { bmatrix }1 & \ \ \ \ \ \ bmatrix } 강체 회전 F = [ 왜냐하면 θ 죄 θ 0 − 죄 θ 왜냐하면 θ 0 0 0 1 ] {\displaystyle \mathbf {F}=cos \theta &\sin \theta &\cos \theta &\cos \theta & 0\0&1\end {bmatrix}} B = C = [ 1 0 0 0 1 0 0 0 1 ] = 1 \displaystyle \mathbf {B} =\mathbf {C} =\mathbf {C} =\mathbf {1} 스트레칭의 도함수 오른쪽 코시-녹색 변형 텐서에 대한 스트레치의 도함수는 많은 고체, 특히 과탄성 물질의 응력-변형 관계를 도출하는 데 사용된다.이러한 파생상품은
∂ λ i ∂ C = 1 2 λ i N i ⊗ N i = 1 2 λ i R T ( n i ⊗ n i ) R ; i = 1 , 2 , 3 {\displaystyle {\displayac \displayda _{i}}=displayac {1}{2\displayda _{i}}~\mathbf {N}_{i}_mathbf {N}_{i}=displayac {1}{2\da _i}}~{mathbf}{i}{i}}{mathbf}{n}{n}}}{mathbf}{n}}{n}}}}{mathbf}{n}}}}}}{math 관찰한 바로는 C : ( N i ⊗ N i ) = λ i 2 ; ∂ C ∂ C = I ( s ) ; I ( s ) : ( N i ⊗ N i ) = N i ⊗ N i . {\displaystyle \mathbf {C} : (\mathbf {N} _{i} \otimes \mathbf {N} _{i} )=\displayda _{i}^2}~;~{\displayac \mathbf {C}} =mathbf {i} {i} {i} {i} {i} {i} }
변형 텐서의 물리적 해석 X = Xi i displaystyle \mathbf {X} =X ^{i}~{\boldsymbol {E}_ { i 가정 = xii{ displaystyle \mathbf {x}~{ symboldsymbol} ( 변형되지 않은 본체의 곡선 style mathbf }(s )}{ displaystyle s\in , 1 style s}{displaystyle \mathbf {x}(s})} 사용 .
곡선의 변형되지 않은 길이는 다음과 같습니다.
l X = ∫ 0 1 d X d s d s = ∫ 0 1 d X d s ⋅ d X d s d s = ∫ 0 1 d X d s ⋅ I ⋅ d X d s d s {\displaystyle l_{X}=\int _{0}^{1}\left {{ds}}\right ~ds=\int _{0}^1}{\cdrt {\cdac {d\mathbf {X}}}{ds}\cdsq {dscds}{ds}{ds}{ds}{ds}{ds}{ds}}}{ds}}}{ds}}}{ds}}}}}}}{ds}}}}}}}}}}} 변형 후에는 길이가 l x = ∫ 0 1 d x d s d s = ∫ 0 1 d x d s ⋅ d x d s d s = ∫ 0 1 ( d x d X ⋅ d X d s ) ⋅ ( d x d X ⋅ d X d s ) d s = ∫ 0 1 d X d s ⋅ [ ( d x d X ) T ⋅ d x d X ] ⋅ d X d s d s {\displaystyle{\begin{정렬}l_{)}&,=\int _{0}^{1}\left{\cfrac{d\mathbf{)}}{ds}}\right ~ds=\int _{0}^{1}{\sqrt{{\cfrac{d\mathbf{)}}{ds}}\cdot{\cfrac{d\mathbf{)}}{ds}}}}~ds=\int _{0}^{1}{\sqrt{\left({\cfrac{d\mathbf{x}}{d\mathbf{X}}}\cdot{\cfrac{d\mathbf{X}}{ds}}\right)\cdot \left({\cfrac{d\mathbf{)}}{d\mathbf{X}}}\cd.고르{ \cdpac {d\mathbf {X}}{ds}\right}}~ds\&=int _{0}^1}{\cdrt {d\cdpac {d\mathbf {X}}{ds}}\cdot \left[\cdpac {d\mathbf {x}}{d\mathbf {x}}}}}}}}{\right}{d\mathbf {d}}}}}}}}}{\mathbf}}}}}}}{\right {T}\cdot {d\mathbf {x} {d\mathbf {X}}\right}\cdot {cfrac {d\mathbf {X}}}}~ds\end {aligned}} 오른쪽 코시-녹색 변형 텐서는 다음과 같이 정의됩니다. C := F T ⋅ F = ( d x d X ) T ⋅ d x d X {\displaystyle {\boldsymbol {C}: = cdot {F} {\boldsymbol {F} = \left({\cfrac {d\mathbf {X} }}}}} \ d\mathbf {X} } ^ {T}\cdot {cfrac {d\mathbf {x}}{d\mathbf {X}}} 이런 이유로, l x = ∫ 0 1 d X d s ⋅ C ⋅ d X d s d s {\displaystyle l_{x}=\int _{0}^{\displayrt {\displayac {d\mathbf {X}}}{ds}}\cdot {cdsymbol {C}}\cdot {ds}{ds}}}}~ds} 이는 길이의 변화가 C(\ displaystyle\boldsymbol {C
유한 변형 텐서 변형률의 개념 은 주어진 변위가 강체 [1] [10] [11] 대규모 변형에 대한 그러한 변형 중 하나는 다음과 같이 정의된 녹색-라그랑주 변형 텐서 또는 녹색-St-Venant 변형 텐서라고도 불리는 라그랑주 유한 변형 텐서이다.
E = 1 2 ( C − I ) 또는 E K L = 1 2 ( ∂ x j ∂ X K ∂ x j ∂ X L − δ K L ) ({displaystyle \mathbf {E} = {1} {2}} (\mathbf {C} - \mathbf {I})\qquad {text {KL} = {1} {2}\left\frac {\frc} {\frac {1} {\fr} {\fr})
또는 변위 경사 텐서의 함수로서
E = 1 2 [ ( ∇ X u ) T + ∇ X u + ( ∇ X u ) T ⋅ ∇ X u ] {\displaystyle \mathbf {E} = flac {1} {2}} \ left[(\sysla _{\mathbf {X} }\mathbf {u})^{ T}+\nabla _{\mathbf {X}}\mathbf {u} +(\nabla _{\mathbf {X}})^{T}\cdot \nabla _{\mathbf {X}}}\mathbf {u} \right} 또는 E K L = 1 2 ( ∂ u K ∂ X L + ∂ u L ∂ X K + ∂ u M ∂ X K ∂ u M ∂ X L ) {\displaystyle E_{KL}=frac {1}{2}}\leftfrac {\partial X_{L}}+{\frac {\frac u_{} L}}{\partial X_{K}}+{\frac {\partial X_{K}}{\frac {\partial u_{M}}{\partial X_{L}}\right}
녹색-라그랑지안 변형률 텐서는 C(\displaystyle mathbf }) (\displaystyle \mathbf \,\!}) 차이
변형 구성을 참조하는 오일러-알만시 유한 변형 텐서. 오일러식 서술은 다음과 같이 정의된다.
e = 1 2 ( I − c ) = 1 2 ( I − B − 1 ) 또는 e r s = 1 2 ( δ r s − ∂ X M ∂ x r ∂ X M ∂ x s ) (\displaystyle \mathbf {e} = flac {1} {2} (\mathbf {I} -\mathbf {B} ^{-1}) qquad {\text{or}\qad e_rs} left {c} ) = frac {1} {frc}
또는 변위 구배의 함수로써 우리가 가지고 있는
e i j = 1 2 ( ∂ u i ∂ x j + ∂ u j ∂ x i − ∂ u k ∂ x i ∂ u k ∂ x j ) ({displaystyle e_{ij}=black {1}{2}}\left\frac {\flac u_{i}}+{\flac {\flac u_{j}}-{\flac u_{i}}-{\flac u_{\frac }){\frac u_{{{\frclac u}}} {\frac u_i}}
라그랑지안과 오일러의 유한 변형률 텐서의 유도 변형 척도는 변형되지 않은 구성의 차분 라인 요소 d (\ displaystyle \mathbf {X} \,!}) 구성 displaystyle mathbf } \,\!}) 차이가 0이 아니면 변형이 발생하고 그렇지 않으면 강체 변위가 발생한 것입니다. 이렇게 해서
d x 2 − d X 2 = d x ⋅ d x − d X ⋅ d X 또는 ( d x ) 2 − ( d X ) 2 = d x j d x j − d X M d X M \displaystyle d\mathbf {x} ^{2}-d\mathbf {x} =d\mathbf {x} -d\mathbf {X} \cdot d\mathbf {X} \qquad {x} \qad {textor}\qad (dx^{x}2-d)
라그랑지안 설명에서 재료 좌표를 기준 프레임으로 사용하여 미분선 사이의 선형 변환은 다음과 같다.
d x = ∂ x ∂ X d X = F d X 또는 d x j = ∂ x j ∂ X M d X M {\displaystyle d\mathbf {x} = flac {\display \mathbf {X} }},d\mathbf {X} =\mathbf {F} \quad {X} \qad {textor}\qad dxj} = frac {x}
그리고 우리는,
d x 2 = d x ⋅ d x = F ⋅ d X ⋅ F ⋅ d X = d X ⋅ F T F ⋅ d X = d X ⋅ C ⋅ d X 또는 ( d x ) 2 = d x j d x j = ∂ x j ∂ X K ∂ x j ∂ X L d X K d X L = C K L d X K d X L {\displaystyle{\begin{정렬}d\mathbf{)}^{2}&, =d\mathbf{)}\cdotd\mathbf{)}\\&, =\mathbf{F}\cdot d\mathbf{X}\cdot \mathbf{F}\cdotd\mathbf{X}\\&, =d\mathbf{X}\cdot \mathbf{F}^{T}\mathbf{F}\cdotd\mathbf{X}\\&, =d\mathbf{X}\cdot\mathbf{C}\cdot d\mathbf{X}\end{정렬}}\qquad{\text{또는}}\qquad{\begin{정렬}(.dx)^{2}&, =dx_{j}\ ,frac_{j}\&=frac {\frac x_{j}{\frac X_{K}}{\frac X_{L}}, dX_{K}, dX_{L}\&=C_{KL}, DX_{K},
여기 K displaystyle }) 오른쪽 Cauchy-Green 변형 텐서, C = F T F displaystyle \mathbf {C} mathbf {F} ^{T}\mathbf {F} ,\!)
d x 2 − d X 2 = d X ⋅ C ⋅ d X − d X ⋅ d X = d X ⋅ ( C − I ) ⋅ d X = d X ⋅ 2 E ⋅ d X {\displaystyle {x}d\mathbf {x}^{2}-d\mathbf {X} ^{2}&=d\mathbf {X} \cdot d\mathbf {X} - d\mathbf {X} \dot d\mathbf {X} \mathbf {X} 또는 ( d x ) 2 − ( d X ) 2 = ∂ x j ∂ X K ∂ x j ∂ X L d X K d X L − d X M d X M = ( ∂ x j ∂ X K ∂ x j ∂ X L − δ K L ) d X K d X L = 2 E K L d X K d X L {\displaystyle {begin{aligned}(dx)^{2}-(dX)^{2}&=frac {\frac {\frac {\frac x_{j}}{\frac {\frac x_{J}}{\frac X_{L}}}, dX_K}, DX_{D}, 여기 E K displaystyle E_{ },\!} Green – St-Venant 스트레인 텐서 또는 Lagrangian 유한 스트레인 텐서라고 불리는 2차 텐서의 구성요소이다. E = 1 2 ( C − I ) 또는 E K L = 1 2 ( ∂ x j ∂ X K ∂ x j ∂ X L − δ K L ) ({displaystyle \mathbf {E} = {1} {2}} (\mathbf {C} - \mathbf {I})\qquad {text {KL} = {1} {2}\left\frac {\frc} {\frac {1} {\fr} {\fr})
오일러식 설명에서, 공간 좌표를 기준 프레임으로 사용하여, 미분 선들 사이의 선형 변환은
d X = ∂ X ∂ x d x = F − 1 d x = H d x 또는 d X M = ∂ X M ∂ x n d x n {\displaystyle d\mathbf {X} = spec frac {\display \mathbf {x} }}d\mathbf {x} =\mathbf {F} ^{-1},d\mathbf {x} =\mathbf {H},d\textbf {x} 여기 서 m X {\ x displaystyle \ frac \ partial _ partial _ are 、 mathbf 、 } 다음 과 같습니다.
d X 2 = d X ⋅ d X = F − 1 ⋅ d x ⋅ F − 1 ⋅ d x = d x ⋅ F − T F − 1 ⋅ d x = d x ⋅ c ⋅ d x 또는 ( d X ) 2 = d X M d X M = ∂ X M ∂ x r ∂ X M ∂ x s d x r d x s = c r s d x r d x s {\displaystyle{\begin{정렬}d\mathbf{X}^{2}&, =d\mathbf{X}\cdotd\mathbf{X}\\&, =\mathbf{F}^{)}\cdot d\mathbf{)}\cdot \mathbf{F}^{)}\cdotd\mathbf{)}\\&, =d\mathbf{)}\cdot \mathbf{F}^{-T}\mathbf{F}^{)}\cdotd\mathbf{)}\\&, =d\mathbf{)}\cdot\mathbf{c}\cdot d\mathbf{)}\end{정렬}}\qquad{\text{또는}}\qquad{.\begin{정렬}( dX) {{2}&=dX_{M},dX_{M}\\&=partial frac {\partial x_{r}}{\frac {\partial x_{M}}}{\partial x_{s}}},{\partial x_{r}},{\partial x_r},{s},{\c}, 여기서 2차 텐서 r displaystyle c_{rs Cauchy의 변형 텐서, c = F T displaystyle mathbf mathbf } mathbf F ^ }
d x 2 − d X 2 = d x ⋅ d x − d x ⋅ c ⋅ d x = d x ⋅ ( I − c ) ⋅ d x = d x ⋅ 2 e ⋅ d x {\displaystyle {cdot {aligned}d\mathbf {x}^{2}&=d\mathbf {x} \cdot \mathbf {x} \cdot d\mathbf {x} \cdot d\mathbf {x} \cdot d\mathbf {x} 또는 ( d x ) 2 − ( d X ) 2 = d x j d x j − ∂ X M ∂ x r ∂ X M ∂ x s d x r d x s = ( δ r s − ∂ X M ∂ x r ∂ X M ∂ x s ) d x r d x s = 2 e r s d x r d x s {\displaystyle {begin{aligned}(dx)^{2}-(dX)^{2}&=frac {j}, {\frac {\partial X_{M}}, {\frac {\frac X_{s}, {\fr}, {\frac}
여기 rs displaystyle e_{ },\!} 오일러-알만시 유한 변형 텐서라고 불리는 2차 텐서의 구성요소이다.
e = 1 2 ( I − c ) 또는 e r s = 1 2 ( δ r s − ∂ X M ∂ x r ∂ X M ∂ x s ) \displaystyle \mathbf {e} = partial frac {1} {2} (\mathbf {I} - \mathbf {c})\qquad {text {or}\qquad e_{rs}=partial frac {r}\left(\frac _ {r}-{r}) {partial}
라그랑지안과 오일러의 유한 변형률 텐서는 모두 변위 구배 텐서로 편리하게 표현될 수 있다. 라그랑지안 변형률 텐서의 경우 먼저 재료 좌표 X X_{M}) 벡터 X , t ) displaystyle mathbf {u}(\mathbf {X},t})} 재료 변위 경사 텐서 δ U (\ displaystyle \nab mathbf}) . } }
u ( X , t ) = x ( X , t ) − X ∇ X u = F − I F = ∇ X u + I 또는 u i = x i − δ i J X J δ i J U J = x i − δ i J X J x i = δ i J ( U J + X J ) ∂ x i ∂ X K = δ i J ( ∂ U J ∂ X K + δ J K ) \displaystyle {\mathbf {u}(\mathbf {X},t)&=\mathbf {x}(\mathbf {X},t)-\mathbf {X} \\mathbf {X} \\mathbf {u} &=\mathbf {F} - mathbf {F} J}\\delta_{iJ}U_{J}&=x_{i}-\delta_{J}\x_{i}&=\delta_{iJ}\left(U_{J}+X_{J}\right)\{frAC_{j}
이 방정식을 라그랑지안 유한 변형률 텐서에 대한 식으로 대체하면 우리는
E = 1 2 ( F T F − I ) = 1 2 [ { ( ∇ X u ) T + I } ( ∇ X u + I ) − I ] = 1 2 [ ( ∇ X u ) T + ∇ X u + ( ∇ X u ) T ⋅ ∇ X u ] \displaystyle {\mathbf {E} &=mathbf {1} {2} \left(\mathbf {F} ^{T}\mathbf {F} -\mathbf {I} \right)\ \&=paramfrac {1}{2}}\left[\left\{(\paramla_{\mathbf {X}}\mathbf {u})^{ T}+\mathbf {I}\right\}\left(\nabla _{\mathbf {X}}}\mathbf {u} +\mathbf {I} \right)-\mathbf {I} \right]\ \&=paramfrac {1}{2}}\left[(\paramla _{\mathbf {X}}\mathbf {u})^{ T}+\nabla _{\mathbf {X}}\mathbf {u} +(\nabla _{\mathbf {X}})^{T}\cdot \nabla _{\mathbf {X}}\mathbf {u}\right] \\end {aligned}} 또는 E K L = 1 2 ( ∂ x j ∂ X K ∂ x j ∂ X L − δ K L ) = 1 2 [ δ j M ( ∂ U M ∂ X K + δ M K ) δ j N ( ∂ U N ∂ X L + δ N L ) − δ K L ] = 1 2 [ δ M N ( ∂ U M ∂ X K + δ M K ) ( ∂ U N ∂ X L + δ N L ) − δ K L ] = 1 2 [ ( ∂ U M ∂ X K + δ M K ) ( ∂ U M ∂ X L + δ M L ) − δ K L ] = 1 2 ( ∂ U K ∂ X L + ∂ U L ∂ X K + ∂ U M ∂ X K ∂ U M ∂ X L ) 디스플레이 스타일 E_{KL}&=frac {1}{2}}\leftfrac {\frac x_{j}{\frac X_{K}}{\frac {\frac X_{L}}-\delta _{KL}\right}\frac {\frac x_{\f} \ & = flac {1} {2} } \ left [ \ frac _ { jM } \ left ( { \ frac { \ partial X _ { K } } + \ delta _ { MK } \ right ) \ delta _ { jN } \ left ( { \ frac { \ frac U _ { { { { { { { { { { { mpartial } } } } } } } } } } } } } } } } } } } \&=frac {1}{2}}\left[\frac {MN}\left({\frac {\partial X_{K}}}+\delta _{MK}\right)\left({\frac {\frac U_{N}}{\fright})_{\fright}_{\fright}NL}_L}_{\fright}_{\fright}_{\frfright}_{\fratial X_{\fr}{\fr} \&=frac {1}{2}}\left[\frac\frac {\partial X_{K}}+\delta _{MK}\right({\frac {\frac U_{M}}})\left({\frac {\partial X_{L}}+delta _ML\right}) \&=frac {1}{2}}\frac {\frac {\frac U_{L}}+{\frac {\frac U_{L}}+{\frac {\frac U_{M}}{\frac {\frac U_{K}}{\frac U_{\frac}
마찬가지로, 오일러-알만시 유한 변형률 텐서는 다음과 같이 표현될 수 있다.
e i j = 1 2 ( ∂ u i ∂ x j + ∂ u j ∂ x i − ∂ u k ∂ x i ∂ u k ∂ x j ) ({displaystyle e_{ij}=black {1}{2}}\left\frac {\flac u_{i}}+{\flac {\flac u_{j}}-{\flac u_{i}}-{\flac u_{\frac }){\frac u_{{{\frclac u}}} {\frac u_i}}
일반 변형률 텐서의 Seth-Hill 패밀리 인도공과대학 의 B. R. 세스 는 그린과 알만시 균주 텐서가 보다 일반적 인 균주 [12] [13] 그 [14] 1968년 로드니 힐에 의해 더욱 확대되었다. 스트레인 측정의 세스-힐 패밀리(도일-에릭슨 [15]
E ( m ) = 1 2 m ( U 2 m − I ) = 1 2 m [ C m − I ] {\displaystyle \mathbf {E} _{(m)} = specfrac {1} {2m} - \mathbf {I} = specfrac {1} {2m} \left [\mathbf {C} ^{m} - \ mathbf {I} \ right }
m의 displaystyle )
그린-라그랑주 변형 텐서 E ( 1 ) = 1 2 ( U 2 − I ) = 1 2 ( C − I ) {\displaystyle \mathbf {E} _{(1)}=mathbf {1}{2} ^{2}-\mathbf {I} =mathbf {C} -\mathbf {I} } 비오트 스트레인 텐서 E ( 1 / 2 ) = ( U − I ) = C 1 / 2 − I {\displaystyle \mathbf {E} _{(1/2)}=(\mathbf {U} -\mathbf {I} )=\mathbf {C}^{1/2}-\mathbf {I} } 로그 변형률, 자연 변형률, 참 변형률 또는 헨키 변형률 E ( 0 ) = 인 U = 1 2 인 C {\displaystyle \mathbf {E} _{(0)}=\ln \mathbf {U} =sqfrac {1}{2}},\ln \mathbf {C} } 알만시균주 E ( − 1 ) = 1 2 [ I − U − 2 ] {\displaystyle \mathbf {E} _{(-1)} = flac {1} {2}} \ left [\mathbf {I} - \mathbf {U} ^{-2} \ right] } 이들 텐서의 2차 근사치는 다음과 같습니다.
E ( m ) = ε + 1 2 ( ∇ u ) T ⋅ ∇ u − ( 1 − m ) ε T ⋅ ε {\displaystyle \mathbf {E} _{(m)}=\tfrac {1}{2}}(\tfrac {u})^{T}\cdot \cdot \mathbf {u} - (1-m){\boldmbol {varepsilon}{\cd}{\cdmbold}{\cdot}{{{{{{cd}) 여기서 displaystyle\boldsymbol\varepsilon})
텐서 (\ displaystyle \mathbf {E}) [16]
모든 (\ displaystyle \mathbf {E}) 변위 경사 텐서 {\ displaystyle \mathbf {E} , . 또한 E(\ displaystyle \mathbf {E}) displaystyle\boldsymbol\varepsilon}) 것 u → displaystyle\displayla\mathbf to 0 예를 들어 텐서 세트입니다.
E ( n ) = ( U n − U − n ) / 2 n {\displaystyle \mathbf {E} ^{(n)}=\leftf\mathbf {U}-{\mathbf {U} }^{-n}\right)/2n} 이 값은 세스-힐 클래스에 속하지 않지만 n(\displaystyle ) [17] = 0 displaystyle =0)
스트레치비 스트레치비 는 차동선 요소의 신장 또는 정상 변형률 측정값으로, 미형성 구성 또는 변형 구성으로 정의할 수 있습니다.
재료점 (\ displaystyle mathbf {N }) 벡터 (\ displaystyle N}) 요소 d = d X N \mathbf N})
Λ ( N ) = d x d X (\displaystyle \Lambda _{(\mathbf {N})}=blac {dx}{dX}}) 여기 displaystyle } dX displaystyle \mathbf {X} \,\!}
마찬가지로 변형 구성의 재료점 \ displaystyle \ mathbf x} 단위 벡터 (\displaystyle mathbf {n}) 요소 x = d n displaystyle \mathbf })
1 Λ ( n ) = d X d x . {\displaystyle {\frac {1}{\Lambda _{\mathbf {n}}}}=squalfrac {dX}{dx}}. }
N({ displaystyle e_{\mathbf {N}}) 정규 변형률 e ({ displaystyle \mathbf {N})
e ( N ) = d x − d X d X = Λ ( N ) − 1. {\displaystyle e_{(\mathbf {N})}=slambda _{\mathbf {N}}-1. }
이 방정식은 스트레칭이 단일성과 동일한 경우 정상 변형률이 0이라는 것을 의미합니다. 즉, 변형은 없습니다. 탄성계와 같은 일부 재료는 고장 나기 전에 3 또는 4의 신축 비율을 유지할 수 있는 반면, 콘크리트나 강철과 같은 기존 엔지니어링 재료는 1.1 정도의 훨씬 낮은 신축 비율에서 고장납니다(참조).
유한 변형률 텐서의 물리적 해석 Lagrangian 유한 변형률 텐서의 대각선 성분 EK (\ displaystyle E_{ })
E 11 = e ( I 1 ) + 1 2 e ( I 1 ) 2 \displaystyle E_{11}=e_{(\mathbf {I}_{1})+{\frac {1}{2}e_{(\mathbf {I}_{1})^2}}
여기 ( I )({ displaystyle e_{\ mathbf {I} _ 1}})} 방향 표준 .
Lagrangian 유한 변형률 텐서의 엇대각선 성분 EK displaystyle { })
E 12 = 1 2 2 E 11 + 1 2 E 22 + 1 죄 ϕ 12 {\displaystyle E_{12}=black {1}{2}}{\sqrt {2E_{11}+1}}{\sin \phi _{12}}
여기 § ({displaystyle phi _{ 방향 ({ displaystyle \mathbf {I} {1}) 2 ({displaystyle \mathbf {I} {2
라그랑지안 유한 스트레인 텐서의 구성요소는 작은 변위율과 같은 특정 상황에서 극소 스트레인 텐서의 구성요소로 근사할 수 있다.
대류 곡선 좌표 변형 텐서 곡선 좌표 에서의 변형 텐서의 표현은 비선형 셸 이론과 큰 플라스틱 변형과 같은 연속체 역학의 많은 문제에 유용하다.x = x ξ 2 3 displaystyle \mathbf {x} mathbf {x} xi 1},\xi 2},\xi 3}}) ( 1 2 3 ^{1}) 좌표는 연속체 내 라그랑지안 입자와 일대일 매핑에 해당하는 경우 "접합"된 것으로 알려져 있다. 좌표 그리드가 초기 구성에서 본체에 "도색"되어 있는 경우, 이 그리드는 변형된 구성의 동일한 재료 입자에 도색된 상태로 유지되도록 재료의 움직임과 함께 흐릅니다. 따라서 그리드 선이 두 구성의 동일한 재료 입자에서 교차합니다. x displaystyle \mathbf {x}} 곡선 .
g i = ∂ x ∂ ξ i (\displaystyle \mathbf {g} _{i}=blac {\displaystyle \mathbf {x} {\xi ^{i}}}) x(\ displaystyle \mathbf {x}) 이 벡터들은 다음과 같은 상호 기저 벡터들과 관련이 있다. g i ⋅ g j = δ i j \displaystyle \mathbf {g}_{i}\cdot \mathbf {g}^{j}=\displaystyle _{i}^{j}}
성분으로 2차 텐서 필드 (\displaystyle\boldsymbol {g})( 일명 메트릭 텐서)를 정의하자.
g i j := ∂ x ∂ ξ i ⋅ ∂ x ∂ ξ j = g i ⋅ g j ({displaystyle g_{ij}): =cdotfrac {cdot \mathbf {x} {\cdot \xi ^{i}} {\cdot \mathbf {g} = {i} \cdot \mathbf {g} _{j}} 첫 번째 종류의 크리스토펠 기호 는 다음과 같이 표현될 수 있다. Γ i j k = 1 2 [ ( g i ⋅ g k ) , j + ( g j ⋅ g k ) , i − ( g i ⋅ g j ) , k ] {\displaystyle \Gamma _{ijk}=sqtfrac {1}{2}}[(\mathbf {g}_{k})_{,j}+(\mathbf {g}_{j}\cdot \mathbf {g}_{k}_i}_{i},cdf {g}_i}_mathbf {g}
Christofel 기호가 오른쪽 코시-녹색 변형 텐서와 어떻게 관련되어 있는지 보기 위해 우리는 유사하게 두 개의 베이스를 정의할 수 있다. 하나는 변형된 그리드 라인에 접하는 베이스이고 다른 하나는 변형되지 않은 그리드 라인에 접하는 것이다. 즉,
G i := ∂ X ∂ ξ i ; G i ⋅ G j = δ i j ; g i := ∂ x ∂ ξ i ; g i ⋅ g j = δ i j \displaystyle \mathbf {G} _{i}: =cdfrac {\mathbf {X} {\mathbf ^{i}}~;~\mathbf {G} _{i}\cdot \mathbf {G} ^{j}=\mathbf {g}~_{i}: =param frac {\param \mathbf {x} {\param \xi ^{i}}~;~\mathbf {g} _{i}\cdot \mathbf {g} ^{j}=\param _{i}^{j}}}}
곡선 좌표의 변형 구배 곡선 좌표에서 벡터장의 구배 정의를 사용하여 변형 구배를 다음과 같이 쓸 수 있습니다.
F = ∇ X x = ∂ x ∂ ξ i ⊗ G i = g i ⊗ G i ({displaystyle {F}}={\mathbf {X}}}\mathbf {x}={\mathbf {x}}{\displaystyle \mathbf {G}^{i}=\mathbf {gimes}_mathbf {ges}) _mathbf {gimes}_i})
곡선 좌표의 오른쪽 코시-녹색 텐서 오른쪽 코시-녹색 변형 텐서는 다음과 같이 주어진다.
C = F T ⋅ F = ( G i ⊗ g i ) ⋅ ( g j ⊗ G j ) = ( g i ⋅ g j ) ( G i ⊗ G j ) ({displaystyle {C}}={F}}^{T}\cdot {\mathbf {G}=(\mathbf {g}_{i})\cdot(\mathbf {g}_{j}\times\mathbf {G})^{j}) C (\ displaystyle\mathbf G }^{i}}) 표현 다음 displaystyle\mathbf i C = C i j G i ⊗ G j {\displaystyle {C}=C_{ij}~\mathbf {G}^{i}\otimes\mathbf {G}^{j} 그러므로, C i j = g i ⋅ g j = g i j \displaystyle C_{ij}=\mathbf {g}_{i}\cdot \mathbf {g}_{j}=g_{ij}
제1종의 대응하는 크리스토펠 기호는 다음과 같은 형태로 표기할 수 있다.
Γ i j k = 1 2 [ C i k , j + C j k , i − C i j , k ] = 1 2 [ ( G i ⋅ C ⋅ G k ) , j + ( G j ⋅ C ⋅ G k ) , i − ( G i ⋅ C ⋅ G j ) , k ] \displaystyle \Gamma _{ijk}=tfrac {1}{2}[C_{ik,j}+C_{jk,i}-C_{ij,k}]=tfrac {1}{2}[(\mathbf {G}_i}_cd {cd\boldsymbol {C}\cd}\cd}\cdf} {CDF}
변형 측도와 크리스토펠 기호 사이의 일부 관계 X = X 1 X 2 X } displaystyle \mathbf {X} X ^ X =x 1 2 } style mathbf { x} x} 으로의 다음 boldsymbol {G}} 및 displaystyle boldsymbol {g}}}
G i j = ∂ X α ∂ x i ∂ X β ∂ x j g α β ({displaystyle G_{ij}={\frac X^{\alpha}}{\frac X^{\beta}}}{\frac X^{j}}~g_{\alpha \alpha }}) 그리고나서, ∂ G i j ∂ x k = ( ∂ 2 X α ∂ x i ∂ x k ∂ X β ∂ x j + ∂ X α ∂ x i ∂ 2 X β ∂ x j ∂ x k ) g α β + ∂ X α ∂ x i ∂ X β ∂ x j ∂ g α β ∂ x k (\displaystyle {\frac G_{ij} {\partial x^{k}}=\leftfrac {\frac x^{2} X^{\alpha}}}~{\frac X^{\frac X^{\beta}}}}+{\frac X^{\frac X}}) ^{i}~{\frac {\partial X^{\beta}}{\frac {\partial x^{j}}~{\frac {\partial g_{\alpha \beta}}}}{\partial x^{k}}}} 주의: ∂ g α β ∂ x k = ∂ X γ ∂ x k ∂ g α β ∂ X γ {\displaystyle {\frac g_{\alpha }}{\frac x^{k}}={\frac x^{k}}~{\frac {\frac g_{\alpha }}}}{\frac X^{\gamma}}}}}}} g α β = g βα {\ display g_{\alpha alpha g_{\alpha ∂ G i j ∂ x k = ( ∂ 2 X α ∂ x i ∂ x k ∂ X β ∂ x j + ∂ 2 X α ∂ x j ∂ x k ∂ X β ∂ x i ) g α β + ∂ X α ∂ x i ∂ X β ∂ x j ∂ X γ ∂ x k ∂ g α β ∂ X γ ∂ G i k ∂ x j = ( ∂ 2 X α ∂ x i ∂ x j ∂ X β ∂ x k + ∂ 2 X α ∂ x j ∂ x k ∂ X β ∂ x i ) g α β + ∂ X α ∂ x i ∂ X β ∂ x k ∂ X γ ∂ x j ∂ g α β ∂ X γ ∂ G j k ∂ x i = ( ∂ 2 X α ∂ x i ∂ x j ∂ X β ∂ x k + ∂ 2 X α ∂ x i ∂ x k ∂ X β ∂ x j ) g α β + ∂ X α ∂ x j ∂ X β ∂ x k ∂ X γ ∂ x i ∂ g α β ∂ X γ {\displaystyle{\begin{정렬}{\frac{\partial G_{ij}}{\partial x^{k}}}&=\left({\frac{\partial ^{2}X^{\alpha}}{\partial x^{나는}\partial x^{k}}}일{\frac{\partial X^{\beta}}{\partial x^{j}}}와{\frac{\partial ^{2}X^{\alpha}}{\partial x^{j}\partial x^{k}}}일{\frac{\partial X^{\beta}}{\partial x^{나는}}}\right)~g_{\alpha \beta}+{\frac{\partial X^.{\al Pha}}{\partial x^{나는}}}~{\frac{\partial X^{\beta}}{\partial x^{j}}}~{\frac{\partial X^{\gamma}}{\partial x^{k}}}~{\frac{\partial g_{\alpha \beta}}{\partial X^{\gamma}}}\\{\frac{\partial G_{ik}}{\partial x^{j}}}&=\left({\frac{\partial ^{2}X^{\alpha}}{\partial x^{나는}\partial x^{j}}}~{\frac{\partial X^{\beta}}{\partial x^{k}}}와{\frac{년.일부 ial ^{2}X^{\alpha}}{\partial x^{j}\partial x^{k}}~{\frac {\partial x^{i}}\right}~g_{\alpha \beta }+{\frac {\partial X^{\alpha}}}~{partial x}}}}}{i}}}}}}{partial xpartial x}}}} {partial}}} {partial}} {\frac}}} {partial}} Artial x^{나는}}}&=\left({\frac{\partial ^{2}X^{\alpha}}{\partial x^{나는}\partial x^{j}}}일{\frac{\partial X^{\beta}}{\partial x^{k}}}와{\frac{\partial ^{2}X^{\alpha}}{\partial x^{나는}\partial x^{k}}}일{\frac{\partial X^{\beta}}{\partial x^{j}}}\right)~g_{\alpha \beta}+{\frac{\partial X^{\alpha}}{\partial x^{j}}}~{\frac{\partial X^{\beta}}{년.일부 ial x^{k}~{\frac {\partial X^{\gamma}}{\partial x^{i}}~{\frac {\partial g_{\alpha \beta}}}{\partial X^{\gamma}}}}\end {\frac}} 정의 ( x ) Γ i j k := 1 2 ( ∂ G i k ∂ x j + ∂ G j k ∂ x i − ∂ G i j ∂ x k ) ( X ) Γ α β γ := 1 2 ( ∂ g α γ ∂ X β + ∂ g β γ ∂ X α − ∂ g α β ∂ X γ ) {\displaystyle\begin{aligned}_{(x)}\Gamma_{ijk}&: ={\frac{1}{2}}\left({\frac{\partial G_{ik}}{\partial x^{j}}}와{\frac{\partial G_{jk}}{\partial x^{나는}}}-{\frac{\partial G_{ij}}{\partial x^{k}}}\right)\\_{(X)}\Gamma _{\alpha \beta \gamma}&은.={\frac{1}{2}}\left({\frac{\partial g_{\alpha)}}{\partial X^{\beta}}}+{\frac{\partial g_{\beta \gamma}}{\partial X^{\alpha}}}-{\frac{\partial g _{\alpha \beta }}{\partial X^{\gamma }}\right)\\end {aligned}} 이런 이유로 ( x ) Γ i j k = ∂ X α ∂ x i ∂ X β ∂ x j ∂ X γ ∂ x k ( X ) Γ α β γ + ∂ 2 X α ∂ x i ∂ x j ∂ X β ∂ x k g α β {\displaystyle _{(x)}\Gamma _{ijk}={\frac X^{\frac X^{\beta}}~{\frac X^{j}}~{\frac X^{\gamma}}{\frac X^{k}}}{{\frac X}}}{\frac X}}}{{{{ijk}}}}}}}}}}}{{\frac X}}}}}}}{{{{{i}}}} 정의 [ G i j ] = [ G i j ] − 1 ; [ g α β ] = [ g α β ] − 1 {\displaystyle [G^{ij}} = [G_{ij}]^{-1}~;~[g^{\alpha \alpha }]=[g_{\alpha \alpha }]^{-1} 그리고나서 G i j = ∂ x i ∂ X α ∂ x j ∂ X β g α β {\displaystyle G^{ij}=gfrac {\frac X^{\alpha }}~{\frac X^{\beta }}~{\frac X^{\beta }}~g^{\alpha \frac }} 두 번째 종류의 크리스토펠 기호를 다음과 같이 정의합니다. ( x ) Γ i j m := G m k ( x ) Γ i j k ; ( X ) Γ α β ν := g ν γ ( X ) Γ α β γ {\displaystyle_{(x)}\Gamma_{ij}^{m}: =G^{mk},_{(x)}\Gamma _{ijk}~;~_{(X)}\Gamma _{\alpha \nu \nu }^{\nu \nu },_{(X)}\Gamma _{\alpha \nu \nu } 그리고나서 ( x ) Γ i j m = G m k ∂ X α ∂ x i ∂ X β ∂ x j ∂ X γ ∂ x k ( X ) Γ α β γ + G m k ∂ 2 X α ∂ x i ∂ x j ∂ X β ∂ x k g α β = ∂ x m ∂ X ν ∂ x k ∂ X ρ g ν ρ ∂ X α ∂ x i ∂ X β ∂ x j ∂ X γ ∂ x k ( X ) Γ α β γ + ∂ x m ∂ X ν ∂ x k ∂ X ρ g ν ρ ∂ 2 X α ∂ x i ∂ x j ∂ X β ∂ x k g α β = ∂ x m ∂ X ν δ ρ γ g ν ρ ∂ X α ∂ x i ∂ X β ∂ x j ( X ) Γ α β γ + ∂ x m ∂ X ν δ ρ β g ν ρ ∂ 2 X α ∂ x i ∂ x j g α β = ∂ x m ∂ X ν g ν γ ∂ X α ∂ x i ∂ X β ∂ x j ( X ) Γ α β γ + ∂ x m ∂ X ν g ν β ∂ 2 X α ∂ x i ∂ x j g α β = ∂ x m ∂ X ν ∂ X α ∂ x i ∂ X β ∂ x j ( X ) Γ α β ν + ∂ x m ∂ X ν δ α ν ∂ 2 X α ∂ x i ∂ x j {\displaystyle{\begin{정렬}_{())}\Gamma _{ij}^{m}&.=G^{mk미만}~{\frac{\partial X^{\alpha}}{\partial x^{나는}}}~{\frac{\partial X^{\beta}}{\partial x^{j}}}~{\frac{\partial X^{\gamma}}{\partial x^{k}}}\,_{(X)}\Gamma _{\alpha \beta \gamma}+G^{mk미만}~{\frac{\partial ^{2}X^{\alpha}}{\partial x^{나는}\partial x^{j}}}~{\frac{\partial X^{\beta}}{\partial. X^{k}}}~g_{\alpha \beta}\\&, ={\frac{\partial x^{m}}{\partial X^{\nu}}}~{\frac{\partial x^{k}}{\partial X^{\rho}}}~g^{\nu \rho}~{\frac{\partial X^{\alpha}}{\partial x^{나는}}}~{\frac{\partial X^{\beta}}{\partial x^{j}}}~{\frac{\partial X^{\gamma}}{\partial x^{k}}}\,_{(X)}\Gamma _{\alpha \beta \gamma}+{\frac{\partial x^{m}}{\partial X^{.\nu }}}~{\frac{\partial x^{k}}{\partial X^{\rho}}}~g^{\nu \rho}~{\frac{\partial ^{2}X^{\alpha}}{\partial x^{나는}\partial x^{j}}}~{\frac{\partial X^{\beta}}{\partial x^{k}}}~g_{\alpha \beta}\\&, ={\frac{\partial x^{m}}{\partial X^{\nu}}}~\delta _{\rho}^{\gamma}~g^{\nu \rho}~{\frac{\partial X^{\alpha}}{\partial x^{나는}}}일{\frac{\partial X^{.\bet A}}{\partial x^{j}}}\,_{(X)}\Gamma _{\alpha \beta \gamma}+{\frac{\partial x^{m}}{\partial X^{\nu}}}~\delta _{\rho}^{\beta}~g^{\nu \rho}~{\frac{\partial ^{2}X^{\alpha}}{\partial x^{나는}\partial x^{j}}}~g_{\alpha \beta}\\&, ={\frac{\partial x^{m}}{\partial X^{\nu}}}~g^{\nu \gamma}~{\frac{\partial X^{\alpha}}{\partial x^{나는}}}일{\frac{\p.arti 알 X^{\beta}}{\partial x^{j}}}\,_{(X)}\Gamma _{\alpha \beta \gamma}+{\frac{\partial x^{m}}{\partial X^{\nu}}}~g^{\nu \beta}~{\frac{\partial ^{2}X^{\alpha}}{\partial x^{나는}\partial x^{j}}}~g_{\alpha \beta}\\&, ={\frac{\partial x^{m}}{\partial X^{\nu}}}~{\frac{\partial X^{\alpha}}{\partial x^{나는}}}~{\frac{\partial X^{\beta}}{\partial x^.{j}} },_{(X)}\Gamma _{\alpha \beta }^{\nu }+{\frac {\partial X^{\nu}}~{\delta _{\alpha }^{\nu }~{\frac {\partial ^2}X^{partial }\i} } 그러므로, ( x ) Γ i j m = ∂ x m ∂ X ν ∂ X α ∂ x i ∂ X β ∂ x j ( X ) Γ α β ν + ∂ x m ∂ X α ∂ 2 X α ∂ x i ∂ x j {\displaystyle _{(x)}\Gamma _{ij}^{m}=blac {\flac X^{\alpha}}~{\flac X^{\alpha}}}~{\flac X^{\beta}}{\flac X^{{\nu}}}}}{{{,}}}}}}}{{\flac X}}}}}}}}}}{{{{\frac}}}}}}}}}}{{{\frac} 매핑의 반전성은 다음을 의미합니다. ∂ X μ ∂ x m ( x ) Γ i j m = ∂ X μ ∂ x m ∂ x m ∂ X ν ∂ X α ∂ x i ∂ X β ∂ x j ( X ) Γ α β ν + ∂ X μ ∂ x m ∂ x m ∂ X α ∂ 2 X α ∂ x i ∂ x j = δ ν μ ∂ X α ∂ x i ∂ X β ∂ x j ( X ) Γ α β ν + δ α μ ∂ 2 X α ∂ x i ∂ x j = ∂ X α ∂ x i ∂ X β ∂ x j ( X ) Γ α β μ + ∂ 2 X μ ∂ x i ∂ x j {\displaystyle{\begin{정렬}{\frac{\partial X^{\mu}}{\partial x^{m}}}\,_{())}\Gamma _{ij}^{m}&, ={\frac{\partial X^{\mu}}{\partial x^{m}}}~{\frac{\partial x^{m}}{\partial X^{\nu}}}~{\frac{\partial X^{\alpha}}{\partial x^{나는}}}~{\frac{\partial X^{\beta}}{\partial x^{j}}}\,_{(X)}\Gamma}_{\alpha \beta}^{\nu}+{\frac{\partial X^{\mu}{.\par Tial x^{m}}}~{\frac{\partial x^{m}}{\partial X^{\alpha}}}~{\frac{\partial ^{2}X^{\alpha}}{\partial x^{나는}\partial x^{j}}}\\&, =\delta _{\nu}^{\mu}~{\frac{\partial X^{\alpha}}{\partial x^{나는}}}~{\frac{\partial X^{\beta}}{\partial x^{j}}}\,_{(X)}\Gamma _{\alpha \beta}^{\nu}+\delta _{\alpha}^{\mu}~{\frac{\partial ^{2}X^{\alpha}}{\parti.알) ^{i}\gamma x^{j}\&=gamfrac {\gamp X^{\alpha}}{\frac {\beta}}{\gamma {\gampa x^{j}},_{(X)}\Gamma _{\alpha \gampa } ^{{\c} } {\frc} x({displaystyle }) 그러므로, ∂ 2 X μ ∂ x i ∂ x j = ∂ X μ ∂ x m ( x ) Γ i j m − ∂ X α ∂ x i ∂ X β ∂ x j ( X ) Γ α β μ ∂ 2 x m ∂ X α ∂ X β = ∂ x m ∂ X μ ( X ) Γ α β μ − ∂ x i ∂ X α ∂ x j ∂ X β ( x ) Γ i j m {\displaystyle{\begin{정렬}{\frac{\partial ^{2}X^{\mu}}{\partial x^{나는}\partial x^{j}}}&={\frac{\partial X^{\mu}}{\partial x^{m}}}\,_{())}\Gamma _{ij}^{m}-{\frac{\partial X^{\alpha}}{\partial x^{나는}}}~{\frac{\partial X^{\beta}}{\partial x^{j}}}\,_{(X)}\Gamma _{\alpha \beta}^{\mu}\\{\frac{\partial ^{2}x^{m}}{\partial X^{\alpha}\par.tial X^{\beta }}&=gamfrac {\beta x^{m},_{(X)},Gamma _{\alpha \mu }^{\frac {\frac x^{i}}-{\frac X^{\alpha }}~{\frac X^{{\frac X}}}}}{{{{{{{{\frac}}}}}}}}}}}}}}}}}}}}{\gamfrac {\gamp}}}}}}}
호환성 조건 연속체 역학의 호환성 문제는 물체에 허용되는 단일값 연속장의 결정을 포함한다. 이러한 허용 조건은 변형 후 신체에 비물리적 간격이나 중복이 없는 상태로 남습니다. 그러한 조건은 대부분 단순하게 연결된 신체에 적용된다. 다중 연결 본체의 내부 경계에 대한 추가 조건이 필요하다.
변형 구배 호환성 단순히 연결된 본체에 호환 displaystyle boldsymbol {F}}
∇ × F = 0 ({displaystyle} {boldsymbol {F}} = boldsymbol {0})
우측 코시-녹색 변형 텐서의 호환성 단순히 연결된 본체에 호환 displaystyle boldsymbol {C}}
R α β ρ γ := ∂ ∂ X ρ [ ( X ) Γ α β γ ] − ∂ ∂ X β [ ( X ) Γ α ρ γ ] + ( X ) Γ μ ρ γ ( X ) Γ α β μ − ( X ) Γ μ β γ ( X ) Γ α ρ μ = 0 {\displaystyle R_{\alpha \rho }^{\rho } : = displayfrac {\rho } {, _{(X)} \Gamma _{\alpha }^{\beta} - {\frac } {\frac } ha \rho }^{\mu }=0} 우리 는 이것들이 리만-크리스토펠 곡률 텐서의 혼합 성분임을 보여줄 수 있다.따라서 C\ display \boldsymbol {C}}- 필요
좌측 코시-녹색 변형 텐서의 호환성 왼쪽 코시-녹색 변형 텐서에 대한 일반적인 충분 조건은 3차원으로 알려져 있지 않다. 2차원 (\ displaystyle\boldsymbol {B}) [18] [19]
「 」를 참조해 주세요. 레퍼런스 ^ a b Lubliner, Jacob (2008). Plasticity Theory (PDF) (Revised ed.). Dover Publications. ISBN 978-0-486-46290-5 the original (PDF) on 2010-03-31. ^ A. Yavari, J.E. Marsden 및 M. Ortis, 탄력성의 공간 및 재료 공변량 균형 법칙 , 수학 물리학 저널, 47, 2006, 042903; 페이지 1~53. ^ Eduardo de Souza Neto; Djordje Peric; Owens, David (2008). Computational methods for plasticity : theory and applications . Chichester, West Sussex, UK: Wiley. p. 65. ISBN 978-0-470-69452-7 ^ IUPAC 는 이 텐서를 코시 스트레인 텐서라고 부를 것을 권장합니다.^ a b c d A. Kaye, R. F. T. Stepto, W. J. Work, J. V. Aleman (Spain), A. Ya. Malkin (1998). "Definition of terms relating to the non-ultimate mechanical properties of polymers" . Pure Appl. Chem . 70 (3): 701–754. doi :10.1351/pac199870030701 {{cite journal }}: CS1 maint: 여러 이름: 작성자 목록(링크 ) ^ 에두아르도 드보킨, 마르셀라 B Goldschmit, 2006 비선형 컨티뉴아, 25페이지, 스프링거 ISBN 3-540-24985-0 . ^ IUPAC 는 이 텐서를 그린 스트레인 텐서라고 부를 것을 권장합니다.^ 밀란 지라섹; 바잔트, Z. P. (2002) 구조물의 비탄성 분석, Wiley , 페이지 463 ISBN 0-471-98716-6 ^ J. N. 레디, 데이비드 K. Gartling (2000 ) 열전달 및 유체역학에서의 유한요소법 , 페이지 317, CRC Press ISBN 1-4200-8598-0 . ^ Belytschko, Ted; Liu, Wing Kam; Moran, Brian (2000). Nonlinear Finite Elements for Continua and Structures (reprint with corrections, 2006 ed.). John Wiley & Sons Ltd. pp. 92–94. ISBN 978-0-471-98773-4 ^ Zeidi, Mahdi; Kim, Chun IL (2018). "Mechanics of an elastic solid reinforced with bidirectional fiber in finite plane elastostatics: complete analysis". Continuum Mechanics and Thermodynamics . 30 (3): 573–592. doi :10.1007/s00161-018-0623-0 . ISSN 1432-0959 . ^ Seth, B. R. (1961), "Generalized strain measure with applications to physical problems" , MRC Technical Summary Report #248 , Mathematics Research Center, United States Army, University of Wisconsin: 1–18, archived from the original on August 22, 2013 ^ Seth, B. R. (1962), "Generalized strain measure with applications to physical problems", IUTAM Symposium on Second Order Effects in Elasticity, Plasticity and Fluid Mechanics, Haifa, 1962. ^ Hill, R. (1968), "On constitutive inequalities for simple materials—I", Journal of the Mechanics and Physics of Solids , 16 (4): 229–242, Bibcode :1968JMPSo..16..229H , doi :10.1016/0022-5096(68)90031-8 ^ T.C. 도일과 J.L. 에릭슨(1956) "비선형 탄성" Applied Mechanics 4, 53–115의 진보 .^ Z.P. 바잔트와 L. 세돌린(1991) 구조물의 안정성. 탄성 이론, 비탄성 이론, 파괴 이론 및 손상 이론. 옥스퍼드 대학교 프레스, 뉴욕 (2차) Dover Publ., New York 2003, 제3판, World Scientific 2010). ^ Z.P. 바잔트(1998). "대칭 역방향 헨키 유한 변형률 및 그 속도를 가진 계산 하기 쉬운 텐서 입니다." 테크놀로지 소재 저널 ASME , 120(4월), 131~136.^ Blume, J. A. (1989). "Compatibility conditions for a left Cauchy–Green strain field". Journal of Elasticity . 21 (3): 271–308. doi :10.1007/BF00045780 . S2CID 54889553 . ^ Acharya, A. (1999). "On Compatibility Conditions for the Left Cauchy–Green Deformation Field in Three Dimensions" (PDF) . Journal of Elasticity . 56 (2): 95–105. doi :10.1023/A:1007653400249 . S2CID 116767781 .
읽고 추가 Dill, Ellis Harold (2006). Continuum Mechanics: Elasticity, Plasticity, Viscoelasticity ISBN 0-8493-9779-0 Dimitrienko, Yuriy (2011). Nonlinear Continuum Mechanics and Large Inelastic Deformations ISBN 978-94-007-0033-8 Hutter, Kolumban; Klaus Jöhnk (2004). Continuum Methods of Physical Modeling ISBN 3-540-20619-1 Lubarda, Vlado A. (2001). Elastoplasticity Theory ISBN 0-8493-1138-1 Macosko, C. W. (1994). Rheology: principles, measurement and applications . VCH Publishers. ISBN 1-56081-579-5 Mase, George E. (1970). Continuum Mechanics ISBN 0-07-040663-4 Mase, G. Thomas; George E. Mase (1999). Continuum Mechanics for Engineers ISBN 0-8493-1855-6 Nemat-Nasser, Sia (2006). Plasticity: A Treatise on Finite Deformation of Heterogeneous Inelastic Materials ISBN 0-521-83979-3 Rees, David (2006). Basic Engineering Plasticity – An Introduction with Engineering and Manufacturing Applications ISBN 0-7506-8025-3 외부 링크 








 공간(랩 프레임) 좌표계의
공간(랩 프레임) 좌표계의 

 강체 변환을 나타내는 변위 벡터입니다.
강체 변환을 나타내는 변위 벡터입니다. 


 변형 구성의 위치까지 확장되는 벡터를
변형 구성의 위치까지 확장되는 벡터를 
 재료(신체 프레임) 좌표계의 기초를 정의하는 단위 벡터입니다.
재료(신체 프레임) 좌표계의 기초를 정의하는 단위 벡터입니다. 



 단위
단위 



 다음과 같습니다
다음과 같습니다




















 고려합니다.
고려합니다.









 다음과 같이 쓸 수 있다.
다음과 같이 쓸 수 있다.
![{\displaystyle {\dot {\mathbf {F} }}={\frac {\partial \mathbf {F} }{\partial t}}={\frac {\partial }{\partial t}}\left[{\frac {\partial \mathbf {x} (\mathbf {X} ,t)}{\partial \mathbf {X} }}\right]={\frac {\partial }{\partial \mathbf {X} }}\left[{\frac {\partial \mathbf {x} (\mathbf {X} ,t)}{\partial t}}\right]={\frac {\partial }{\partial \mathbf {X} }}\left[\mathbf {V} (\mathbf {X} ,t)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2666606a9db3c727de1e94fa372b590683f72c0)
 (물질) 속도입니다.오른쪽에 있는 도함수는 재료 속도 구배를 나타냅니다.도함수에 대한 연쇄 규칙을 적용하여 이를 공간 구배로 변환하는 것이 일반적이다.
(물질) 속도입니다.오른쪽에 있는 도함수는 재료 속도 구배를 나타냅니다.도함수에 대한 연쇄 규칙을 적용하여 이를 공간 구배로 변환하는 것이 일반적이다.![{\displaystyle {\dot {\mathbf {F} }}={\frac {\partial }{\partial \mathbf {X} }}\left[\mathbf {V} (\mathbf {X} ,t)\right]={\frac {\partial }{\partial \mathbf {X} }}\left[\mathbf {v} (\mathbf {x} (\mathbf {X} ,t),t)\right]=\left.{\frac {\partial }{\partial \mathbf {x} }}\left[\mathbf {v} (\mathbf {x} ,t)\right]\right|_{\mathbf {x} =\mathbf {x} (\mathbf {X} ,t)}\cdot {\frac {\partial \mathbf {x} (\mathbf {X} ,t)}{\partial \mathbf {X} }}={\boldsymbol {l}}\cdot \mathbf {F} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/abbb3bd21a0c39cedc504214b5bb20503386c081)
 공간 속도 구배이며
공간 속도 구배이며 공간(Ulerian 속도
공간(Ulerian 속도







 변형된 구성에서 영역의 영역,
변형된 구성에서 영역의 영역, 

 외부 법선입니다.기준 구성에서
외부 법선입니다.기준 구성에서 

















 것을 의미합니다.
것을 의미합니다. 









 불변량이 자주 사용됩니다.가장 일반적으로 사용되는
불변량이 자주 사용됩니다.가장 일반적으로 사용되는 ![{\displaystyle {\begin{aligned}I_{1}^{C}&:={\text{tr}}(\mathbf {C} )=C_{II}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}\\I_{2}^{C}&:={\tfrac {1}{2}}\left[({\text{tr}}~\mathbf {C} )^{2}-{\text{tr}}(\mathbf {C} ^{2})\right]={\tfrac {1}{2}}\left[(C_{JJ})^{2}-C_{IK}C_{KI}\right]=\lambda _{1}^{2}\lambda _{2}^{2}+\lambda _{2}^{2}\lambda _{3}^{2}+\lambda _{3}^{2}\lambda _{1}^{2}\\I_{3}^{C}&:=\det(\mathbf {C} )=J^{2}=\lambda _{1}^{2}\lambda _{2}^{2}\lambda _{3}^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d05cca3762fe510c6252312cb22a66da138cfef)
 변형
변형 



 불변량도 사용된다.일반적인 불변량은 다음과 같이 정의된다.
불변량도 사용된다.일반적인 불변량은 다음과 같이 정의된다.![{\displaystyle {\begin{aligned}I_{1}&:={\text{tr}}(\mathbf {B} )=B_{ii}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}\\I_{2}&:={\tfrac {1}{2}}\left[({\text{tr}}~\mathbf {B} )^{2}-{\text{tr}}(\mathbf {B} ^{2})\right]={\tfrac {1}{2}}\left(B_{ii}^{2}-B_{jk}B_{kj}\right)=\lambda _{1}^{2}\lambda _{2}^{2}+\lambda _{2}^{2}\lambda _{3}^{2}+\lambda _{3}^{2}\lambda _{1}^{2}\\I_{3}&:=\det \mathbf {B} =J^{2}=\lambda _{1}^{2}\lambda _{2}^{2}\lambda _{3}^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e88d7c726ee801990cc0dda3221b4a2edc04aa5)

























![s\in [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/aff1a54fbbee4a2677039524a5139e952fa86eb9)
 파라미터화 합니다
파라미터화 합니다

![{\displaystyle {\begin{aligned}l_{x}&=\int _{0}^{1}\left|{\cfrac {d\mathbf {x} }{ds}}\right|~ds=\int _{0}^{1}{\sqrt {{\cfrac {d\mathbf {x} }{ds}}\cdot {\cfrac {d\mathbf {x} }{ds}}}}~ds=\int _{0}^{1}{\sqrt {\left({\cfrac {d\mathbf {x} }{d\mathbf {X} }}\cdot {\cfrac {d\mathbf {X} }{ds}}\right)\cdot \left({\cfrac {d\mathbf {x} }{d\mathbf {X} }}\cdot {\cfrac {d\mathbf {X} }{ds}}\right)}}~ds\\&=\int _{0}^{1}{\sqrt {{\cfrac {d\mathbf {X} }{ds}}\cdot \left[\left({\cfrac {d\mathbf {x} }{d\mathbf {X} }}\right)^{T}\cdot {\cfrac {d\mathbf {x} }{d\mathbf {X} }}\right]\cdot {\cfrac {d\mathbf {X} }{ds}}}}~ds\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd1b639bab0e25d96cf46894973e1d2693800d94)




![{\displaystyle \mathbf {E} ={\frac {1}{2}}\left[(\nabla _{\mathbf {X} }\mathbf {u} )^{T}+\nabla _{\mathbf {X} }\mathbf {u} +(\nabla _{\mathbf {X} }\mathbf {u} )^{T}\cdot \nabla _{\mathbf {X} }\mathbf {u} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/613f67ee25337f305e0fe930e90f5099becdc913)
















 Cauchy의 변형
Cauchy의 변형 





 미분하여 재료 변위 경사 텐서
미분하여 재료 변위 경사 텐서

![{\displaystyle {\begin{aligned}\mathbf {E} &={\frac {1}{2}}\left(\mathbf {F} ^{T}\mathbf {F} -\mathbf {I} \right)\\&={\frac {1}{2}}\left[\left\{(\nabla _{\mathbf {X} }\mathbf {u} )^{T}+\mathbf {I} \right\}\left(\nabla _{\mathbf {X} }\mathbf {u} +\mathbf {I} \right)-\mathbf {I} \right]\\&={\frac {1}{2}}\left[(\nabla _{\mathbf {X} }\mathbf {u} )^{T}+\nabla _{\mathbf {X} }\mathbf {u} +(\nabla _{\mathbf {X} }\mathbf {u} )^{T}\cdot \nabla _{\mathbf {X} }\mathbf {u} \right]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1bc4d02e18262b73b16470e4e4cfb36c933410b)
![{\displaystyle {\begin{aligned}E_{KL}&={\frac {1}{2}}\left({\frac {\partial x_{j}}{\partial X_{K}}}{\frac {\partial x_{j}}{\partial X_{L}}}-\delta _{KL}\right)\\&={\frac {1}{2}}\left[\delta _{jM}\left({\frac {\partial U_{M}}{\partial X_{K}}}+\delta _{MK}\right)\delta _{jN}\left({\frac {\partial U_{N}}{\partial X_{L}}}+\delta _{NL}\right)-\delta _{KL}\right]\\&={\frac {1}{2}}\left[\delta _{MN}\left({\frac {\partial U_{M}}{\partial X_{K}}}+\delta _{MK}\right)\left({\frac {\partial U_{N}}{\partial X_{L}}}+\delta _{NL}\right)-\delta _{KL}\right]\\&={\frac {1}{2}}\left[\left({\frac {\partial U_{M}}{\partial X_{K}}}+\delta _{MK}\right)\left({\frac {\partial U_{M}}{\partial X_{L}}}+\delta _{ML}\right)-\delta _{KL}\right]\\&={\frac {1}{2}}\left({\frac {\partial U_{K}}{\partial X_{L}}}+{\frac {\partial U_{L}}{\partial X_{K}}}+{\frac {\partial U_{M}}{\partial X_{K}}}{\frac {\partial U_{M}}{\partial X_{L}}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8613306031cc1580236c979b6aec6c795d3e4db9)
![{\displaystyle \mathbf {E} _{(m)}={\frac {1}{2m}}(\mathbf {U} ^{2m}-\mathbf {I} )={\frac {1}{2m}}\left[\mathbf {C} ^{m}-\mathbf {I} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70e3f0b7ddba558d16a401580cf534133ef24d09)
 다음과 같은 것이 있습니다.
다음과 같은 것이 있습니다.


![{\displaystyle \mathbf {E} _{(-1)}={\frac {1}{2}}\left[\mathbf {I} -\mathbf {U} ^{-2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0446d9edf116c655919b58ac4fc46fab8778af99)

 극소 변형률 텐서입니다.
극소 변형률 텐서입니다.  다른 많은 정의는 모두
다른 많은 정의는 모두  연속적이고
연속적이고

 세스-힐 측정값과 2차 근사값이 같다.
세스-힐 측정값과 2차 근사값이 같다.


 차분 요소
차분 요소 




 정상 변형률과 관련이 있습니다.
정상 변형률과 관련이 있습니다.

 I
I 

 I
I 





 단위 벡터입니다.
단위 벡터입니다. 













 좌표
좌표




![{\displaystyle \Gamma _{ijk}={\tfrac {1}{2}}[(\mathbf {g} _{i}\cdot \mathbf {g} _{k})_{,j}+(\mathbf {g} _{j}\cdot \mathbf {g} _{k})_{,i}-(\mathbf {g} _{i}\cdot \mathbf {g} _{j})_{,k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c84f52a8b94bf81096fd54ad218ac8c8a794593)






![{\displaystyle \Gamma _{ijk}={\tfrac {1}{2}}[C_{ik,j}+C_{jk,i}-C_{ij,k}]={\tfrac {1}{2}}[(\mathbf {G} _{i}\cdot {\boldsymbol {C}}\cdot \mathbf {G} _{k})_{,j}+(\mathbf {G} _{j}\cdot {\boldsymbol {C}}\cdot \mathbf {G} _{k})_{,i}-(\mathbf {G} _{i}\cdot {\boldsymbol {C}}\cdot \mathbf {G} _{j})_{,k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/626053366fba8dffc9ee988c8728f9b476cee63a)









![{\displaystyle [G^{ij}]=[G_{ij}]^{-1}~;~~[g^{\alpha \beta }]=[g_{\alpha \beta }]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6168f5195b650daf063a1dd26b314242926f774)









![{\displaystyle R_{\alpha \beta \rho }^{\gamma }:={\frac {\partial }{\partial X^{\rho }}}[\,_{(X)}\Gamma _{\alpha \beta }^{\gamma }]-{\frac {\partial }{\partial X^{\beta }}}[\,_{(X)}\Gamma _{\alpha \rho }^{\gamma }]+\,_{(X)}\Gamma _{\mu \rho }^{\gamma }\,_{(X)}\Gamma _{\alpha \beta }^{\mu }-\,_{(X)}\Gamma _{\mu \beta }^{\gamma }\,_{(X)}\Gamma _{\alpha \rho }^{\mu }=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29e1d54640569dc6ab58c0fca0c0ab634aef2180)



