플라즈마 진동

플라즈마 진동은 (Irving Langmuir의 이름을 따서) Langmuir 파동이라고도 하며, 자외선 영역에서 플라즈마나 금속과 같은 전도 매체에서 전자 밀도의 빠른 진동입니다.진동은 자유 전자 가스의 유전체 기능의 불안정성으로 설명할 수 있습니다.주파수는 진동 파장에 따라 약하게만 달라집니다.이러한 진동의 양자화에서 생기는 준입자가 플라즈몬이다.

랭뮤어파는 1920년대 ^[1]미국 물리학자 어빙 랭뮤어와 루이 통크스에 의해 발견되었다.정적 매체의 중력 불안정성에 의해 발생하는 청바지 불안정파와 형태가 평행합니다.

메커니즘

양전하를 띤 이온과 음전하를 띤 전자의 기체로 구성된 평형 상태의 전기 중성 플라즈마를 생각해 보십시오.이온에 대해 전자 또는 전자 그룹을 아주 작은 양만큼 이동시키면 쿨롱 힘이 전자를 끌어당겨 복원력으로 작용한다.

'차가운' 전자

전자의 열 운동을 무시하면 전하 밀도가 플라즈마 주파수로 진동한다는 것을 보여줄 수 있습니다.

\omega _{\mathrm {pe} }={\sqrt {\frac {n_{\mathrm {e} }e^{2}}{m^{*}\varepsilon _{0}}}},\left[\mathrm {rad/s} \right]

\omega _{\mathrm {pe} }={\sqrt {\frac {n_{\mathrm {e} }e^{2}}{m^{*}\varepsilon _{0}}}},\left[\mathrm {rad/s} \right]

e

\omega _{\mathrm {pe} }={\sqrt {\frac {n_{\mathrm {e} }e^{2}}{m^{*}\varepsilon _{0}}}},\left[\mathrm {rad/s} \right]

=

\omega _{\mathrm {pe} }={\sqrt {\frac {n_{\mathrm {e} }e^{2}}{m^{*}\varepsilon _{0}}}},\left[\mathrm {rad/s} \right]

\omega _{\mathrm {pe} }={\sqrt {\frac {n_{\mathrm {e} }e^{2}}{m^{*}\varepsilon _{0}}}},\left[\mathrm {rad/s} \right]

2 m

\omega _{\mathrm {pe} }={\sqrt {\frac {n_{\mathrm {e} }e^{2}}{m^{*}\varepsilon _{0}}}},\left[\mathrm {rad/s} \right]

∗

\omega _{\mathrm {pe} }={\sqrt {\frac {n_{\mathrm {e} }e^{2}}{m^{*}\varepsilon _{0}}}},\left[\mathrm {rad/s} \right]

, [

r

/

\omega _{\mathrm {pe} }={\sqrt {\frac {n_{\mathrm {e} }e^{2}}{m^{*}\varepsilon _{0}}}},\left[\mathrm {rad/s} \right]

s

\omega _{\mathrm {pe} }={\sqrt {\frac {n_{\mathrm {e} }e^{2}}{m^{*}\varepsilon _{0}}}},\left[\mathrm {rad/s} \right]

]{

displaystyle

\ omega _ { \

mathrm

{ e }

= rt

{

frac

{

n

_ { \

mathrm

{

e

} } e^ {

}

{

m^

{ * } \

varepsilon _

{ 0 } } } , \ left [ \ mathright

\omega _{\mathrm {pe} }={\sqrt {\frac {n_{\mathrm {e} }e^{2}}{m^{*}\varepsilon _{0}}}},\left[\mathrm {rad/s} \right]

}

\omega _{\mathrm {pe} }={\sqrt {\frac {n_{\mathrm {e} }e^{2}}{m^{*}\varepsilon _{0}}}},\left[\mathrm {rad/s} \right]

} } }

、

\

mathright

。

ω pe)4π nee2m∗,({\displaystyle \omega_{\mathrm{pe}}={\sqrt{\frac{4\pi n_{\mathrm{e}}e^{2}}{m^{*}}}},\left[\mathrm{rad/s}\right]}(cgs대),.

전자의 여기서 ne{\displaystyle n_{\mathrm{e}}}은 전자의 수 밀도, e{\displaystyle e}은 전하, m({\displaystyle m^{*}}은 유효 질량, 그리고 자유 공간의 0{\displaystyle \varepsilon_{0}}은 유전율 ε.위 공식은 근사는 이온 질량 무한한 하에 파생된 점에 유의한다.이것은 일반적으로 아주 비슷해, 전자들이 너무 많이 이온보다 가볍다.

프루프 맥스웰 방정식을 사용해.[노트 1]라고 가정하면 전하 밀도 진동 ρ(ω))ρ 0e− 나는 t{\displaystyle \rho(\omega)=\rho_{0}e^{-i\omega지}}이 연속 방정식 ω:.

\cdot \mathbf {j} =-{\frac \rho }{\frac t}=i\Omega \rho(\obega)

가우스법

\displaystyle \cdot \mathbf {E} (\mega)=4\pi \rho (\mega)}

전도성

\displaystyle \mathbf {j}(\obega)=\mathbf {E}(\obega)}

남아 있습니다.

(\displaystyle i\obega \rho (\obega)=4\pi \pi (\obega)\rho (\obega)}

그것은 항상 진실이다

1+{\frac {4\piii\display(\mega)}{\opega}}=0

$\epsilon (\omega )=1+{\frac {4\pi i\sigma (\omega )}{\omega }}$ 이는 유전율( $\epsilon (\omega )=1+{\frac {4\pi i\sigma (\omega )}{\omega }}$ 모델 참조) $\epsilon (\omega )=1+{\frac {4\pi i\sigma (\omega )}{\omega }}$ ( $\epsilon (\omega )=1+{\frac {4\pi i\sigma (\omega )}{\omega }}$ ) $=$ + $\epsilon (\omega )=1+{\frac {4\pi i\sigma (\omega )}{\omega }}$ $\epsilon (\omega )=1+{\frac {4\pi i\sigma (\omega )}{\omega }}$ i $\epsilon (\omega )=1+{\frac {4\pi i\sigma (\omega )}{\omega }}$ ( $\epsilon (\omega )=1+{\frac {4\pi i\sigma (\omega )}{\omega }}$ \ $display$ $style$ \ $silon$ ( \ $omega$ ) = 1 + { \ $frac$ { $4$ \ $pi$ i \ $silon$ $\epsilon \geq 0$ ( \ $flac }$ { \ $obe$ } $\epsilon (\omega )=1+{\frac {4\pi i\sigma (\omega )}{\omega }}$ } $the$ the ( $\epsilon \geq 0$ displayeeeeedisplay e e e edisplay display display e $\epsilon \geq 0$ display $\epsilon \geq 0$ e e e display e $\epsilon \geq 0$ e e display display e e e e e e e displaydisplay $\omega _{\rm {p}}$ 전하 밀도에서 밀도 파형의 전파를 가능하게 하기 위해 $\epsilon =0$ 서 $\epsilon =0$ $=$ 0(\ $displaystyle \silon$ = $0)$ 과 $\epsilon = 0$ 동일한 조건이 적용된다.

^ 애쉬크로프트 & 머먼 1976, 19페이지

이 표현은 천체물리학에서 ^[2]자주 볼 수 있는 전자-양전자 플라스마의 경우 수정되어야 한다.주파수는 파장과 독립적이기 때문에 이러한 진동은 위상 속도가 무한하고 그룹 속도가 0입니다.

m $m^{*}=m_{\mathrm {e} }$ $m^{*}=m_{\mathrm {e} }$ $m^{*}=m_{\mathrm {e} }$ {\ $displaystyle$ m^{*} $= m_{\mathrm {e$ 일 때 플라즈마 주파수 $\omega _{\mathrm {pe} }$ p $\omega _{\mathrm {pe} }$ {\ $displaystyle \obega _{\mathrm$ ${e$ $\omega _{\mathrm {pe} }$ 는 물리 상수와 전자 $n_{\mathrm {e} }$ $n_{\mathrm {e} }$ ${\$ {e $n_{\mathrm {e} }$ 에만 의존합니다.각 플라즈마 주파수의 수치식은 다음과 같습니다.

f_{\text{pe}} = flac {\text{pe}}{2\pi}}~\left[{\text{Hz}}\right]

금속은 금속의 플라즈마 주파수보다 높은 주파수의 빛에만 투명합니다.알루미늄 또는 은과 같은 일반적인 금속의 경우 $(\$ 은 $n_{{\mathrm {e}}}$ 약²³ 10cm이며⁻³, 이로 인해 플라즈마 주파수가 자외선 영역으로 유입됩니다.이것이 대부분의 금속이 가시광선을 반사하고 빛나는 것처럼 보이는 이유입니다.

'따뜻한' 전자

전자 $v_{\mathrm {e,th} }={\sqrt {\frac {k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}}$ $v_{\mathrm {e,th} }={\sqrt {\frac {k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}}$ $v_{\mathrm {e,th} }={\sqrt {\frac {k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}}$ e의 영향을 $v_{\mathrm {e,th} }={\sqrt {\frac {k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}}$ 할 때 $v_{\mathrm {e,th} }={\sqrt {\frac {k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}}$ h $v_{\mathrm {e,th} }={\sqrt {\frac {k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}}$ $v_{\mathrm {e,th} }={\sqrt {\frac {k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}}$ $v_{\mathrm {e,th} }={\sqrt {\frac {k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}}$ $v_{\mathrm {e,th} }={\sqrt {\frac {k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}}$ $v_{\mathrm {e,th} }={\sqrt {\frac {k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}}$ $v_{\mathrm {e,th} }={\sqrt {\frac {k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}}$ e $v_{\mathrm {e,th} }={\sqrt {\frac {k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}}$ { $displaystyle$ v $_$ { \ $mathrm { e$ , $th$ } = $sqrt$ { $frac$ { k $_$ { \ $mathrm$ { $B }$ } }} { $m$ _ { \ $mathrm$ { $e }}}}$ = rtrcrcrcrcrt { k_{ k _ rt { k_{ k_{\ mathrm { k_{\ mathrm } } } } } } } } restore restore종방향 Langmuir^[3] 파형과 관련된 ih 주파수 및 파형 수:

\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2}

2

\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2}

=

ω

\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2}

e

\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2}

+

\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2}

k

\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2}

T

\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2}

\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2}

\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2}

=

p

p

\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2}

\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2}

+

\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2}

\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2}

\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2}

e ,

\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2}

2 \

displaystyle

\

omega

^{2

} =

\

obega

_ { \

mathrm

{ B

}

+ { \ frac {

3

k _ { \

mathrm

{ B } } {

m

}

}

}

Bohm-Gross 분산 관계라고 불립니다.공간 스케일이 데바이의 길이에 비해 클 경우 진동은 압력 항에 의해 약하게 변화될 뿐이지만, 작은 스케일에서는 압력 항이 우세하고 ${\sqrt {3}}\cdot v_{\mathrm {e,th} }$ e ${\sqrt {3}}\cdot v_{\mathrm {e,th} }$ ${\sqrt {3}}\cdot v_{\mathrm {e,th} }$ ${\sqrt {3}}\cdot v_{\mathrm {e,th} }$ {\ $displaystyle$ {\ $sqrt {3}}\cdot v_{\mathrm {e,th$ 의 ${\sqrt {3}}\cdot v_{\mathrm {e,th} }$ 로 파동이 분산되지 않습니다. 단, 이러한 파동의 경우 t는 전자입니다.헤르말 속도는 위상 속도에 필적합니다.

{\displaystyle v\sim v_{\mathrm {ph}\stackrel {def}{=}\frac {mega}{k}},

그래서 플라즈마 파장은 파장의 위상 속도와 거의 같은 속도로 움직이는 전자를 가속시킬 수 있다.이 과정은 종종 란다우 댐핑이라고 불리는 무충돌 댐핑의 형태로 이어집니다.따라서 분산관계에서 대k부분은 관찰하기 어렵고 거의 중요하지 않다.

유계 플라즈마에서 프링킹 전장은 전자가 차가울 때에도 플라즈마 진동의 전파를 일으킬 수 있습니다.

금속 또는 반도체에서는 이온의 주기적 전위의 영향을 고려해야 한다.이것은 보통 m 대신에 전자의 유효 질량을 사용함으로써 이루어진다.

플라즈마 진동 및 음질량의 영향

그림 1

m_{2}

({

의 코어는

m_{2}

({

2})의

k_{2}

스프링을 통해

m_{1}

({

의 셸에 내부적으로 연결되어 있습니다.

F(t)={\widehat {F}}\sin \omega t

은

F(t)={\widehat {F}}\sin \omega t

F

F(t)={\widehat {F}}\sin \omega t

(

F(t)={\widehat {F}}\sin \omega t

)

F(t)={\widehat {F}}\sin \omega t

F(t)={\widehat {F}}\sin \omega t

^ sin

F(t)={\widehat {F}}\sin \omega t

F(t)={\widehat {F}}\sin \omega t

{

displaystyle

F(t) =

widehat {F}\sin \obega

t

F(t)={\widehat {F}}\sin \omega t

의 영향을 받습니다.

플라즈마 진동은 "음질량"의 효과를 일으킬 수 있습니다.음의 유효 질량 효과를 발생시키는 기계적 모델은 그림 1에 나와 있다. $m_{2}$ $({$ 의 $m_{2}$ 코어는 $k_{2}$ $({$ 의 $k_{2}$ 스프링을 통해 $m_{1}$ $({$ 의 셸에 내부적으로 연결되어 있습니다.시스템은 외부 $F(t)={\widehat {F}}\sin \omega t$ F ( $F(t)={\widehat {F}}\sin \omega t$ ) $F(t)={\widehat {F}}\sin \omega t$ ^ sin $F(t)={\widehat {F}}\sin \omega t$ ⁡ $F(t)={\widehat {F}}\sin \omega t$ t { $display$ F ( t ) = $widehat$ { $F$ } } \ $sin$ \ $obega$ t $F(t)={\widehat {F}}\sin \omega t$ 를 받는다. $m_{1}$ m $m_{1}$ ({ $displaystyle m_1})$ 및 $m_{1}$ $m_{2}$ 2 ({ $displaystyle m_2})$ 에 $m_{2}$ 대한 운동 방정식을 풀면 전체 시스템을 유효 $m_{\rm {eff}}$ $m_{\rm {eff}}$ 로 대체한다. $m_{\rm {eff}}$ (\ $displaystyle$ m_ ${\rm$ {filename $}})$ 다음 $m_{\rm {eff}}$ 정보를 얻습니다.^[4]^[5]^[6]^[7]^[8]

$m_{\rm {eff}}=m_{1}+{m_{2}\omega _{0}^{2} \over \omega _{0}^{2}-\omega ^{2}}$ e $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{0}^{2} \over \omega _{0}^{2}-\omega ^{2}}$ $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{0}^{2} \over \omega _{0}^{2}-\omega ^{2}}$ $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{0}^{2} \over \omega _{0}^{2}-\omega ^{2}}$ 1 $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{0}^{2} \over \omega _{0}^{2}-\omega ^{2}}$ + $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{0}^{2} \over \omega _{0}^{2}-\omega ^{2}}$ 2 $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{0}^{2} \over \omega _{0}^{2}-\omega ^{2}}$ $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{0}^{2} \over \omega _{0}^{2}-\omega ^{2}}$ 2 $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{0}^{2} \over \omega _{0}^{2}-\omega ^{2}}$ 0 $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{0}^{2} \over \omega _{0}^{2}-\omega ^{2}}$ 2 - $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{0}^{2} \over \omega _{0}^{2}-\omega ^{2}}$ 0 2 - $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{0}^{2} \over \omega _{0}^{2}-\omega ^{2}}$ 0 2 、 ${$ $displaystyle$ m $_$ { \ rm { $rm } =$ m _ { $1}$ + { $m _$ { 0 $}^2} \over$ \ （ 0 $）^2}$ - \ $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{0}^{2} \over \omega _{0}^{2}-\omega ^{2}}$

여기서 $\omega _{0}={\sqrt {k_{2} \over m_{2}}}$ 0 $\omega _{0}={\sqrt {k_{2} \over m_{2}}}$ $\omega _{0}={\sqrt {k_{2} \over m_{2}}}$ $\omega _{0}={\sqrt {k_{2} \over m_{2}}}$ $\omega _{0}={\sqrt {k_{2} \over m_{2}}}$ {{ $0} = rt {k_{2}$ $\over$ m_ ${$ $2$ $m_{\rm {eff}}$ $m_{\rm {eff}}$ $m_{\rm {eff}}$ {{ $displaystyle m_{rm}}$ 위에서 $\omega _{0}$ $m_{\rm {eff}}$ 주파수 $\omega$ { $displaystyle \obe$ $}$ 이 $\omega$ (가) $\omega _{0}$ 0에 가까워지면 ^[4]^[5]^[6]^[7]음수가 됩니다.

그림 2자유 전자

m_{2}

({

는

m_{2}

이온

m_{1}

({

에 내장되어 있습니다.

\omega _{\rm {p}}

p

\omega _{\rm {p}}

{

displaystyle

\

obega

_

{\rm {p}}

는

\omega _{\rm {p}}

플라즈마 주파수입니다(왼쪽 스케치).시스템의 동등한 기계적 구성표(오른쪽 스케치).

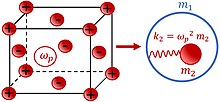
음의 유효 질량(밀도)도 자유 전자 가스의 플라즈마 진동을 이용하는 전기 기계 결합에 기초해 가능하게 된다(그림 ^[8]^[9]2 참조).음의 질량은 전자 $m_{2}$ $m_{2}$ 의 $m_{2}$ 플라즈마 진동 주파수({ $displaystyle m_{2})$ 와 $m_{2}$ 이온 $m_{1}$ $({$ 에 근접한 $({displaystyle \obe})$ 의 $\omega$ 금속 입자의 진동으로 나타난다.플라즈마 진동은 탄성 $k_{2}=\omega _{\rm {p}}^{2}m_{2}$ $k_{2}=\omega _{\rm {p}}^{2}m_{2}$ $=$ $k_{2}=\omega _{\rm {p}}^{2}m_{2}$ $k_{2}=\omega _{\rm {p}}^{2}m_{2}$ $k_{2}=\omega _{\rm {p}}^{2}m_{2}$ {\ $displaystyle k_{2$ }=\ $obega$ _ ${\$ $rm$ { $p}}{{2}m_{2$ 로 $\omega _{\rm {p}}$ 표현됩니다. $\omega _{\rm {p}}$ 서 δ $\omega _{\rm {p}}$ p \ $displaystyle \obe$ {\rm ${p}}$ 은 플라즈마 주파수입니다.따라서 외부주파수 θ로 진동하는 금속입자는 유효질량으로 표현된다.

$m_{\rm {eff}}=m_{1}+{m_{2}\omega _{\rm {p}}^{2} \over \omega _{\rm {p}}^{2}-\omega ^{2}}$ e $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{\rm {p}}^{2} \over \omega _{\rm {p}}^{2}-\omega ^{2}}$ $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{\rm {p}}^{2} \over \omega _{\rm {p}}^{2}-\omega ^{2}}$ $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{\rm {p}}^{2} \over \omega _{\rm {p}}^{2}-\omega ^{2}}$ 1 $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{\rm {p}}^{2} \over \omega _{\rm {p}}^{2}-\omega ^{2}}$ + $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{\rm {p}}^{2} \over \omega _{\rm {p}}^{2}-\omega ^{2}}$ $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{\rm {p}}^{2} \over \omega _{\rm {p}}^{2}-\omega ^{2}}$ $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{\rm {p}}^{2} \over \omega _{\rm {p}}^{2}-\omega ^{2}}$ p $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{\rm {p}}^{2} \over \omega _{\rm {p}}^{2}-\omega ^{2}}$ $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{\rm {p}}^{2} \over \omega _{\rm {p}}^{2}-\omega ^{2}}$ $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{\rm {p}}^{2} \over \omega _{\rm {p}}^{2}-\omega ^{2}}$ 2 - $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{\rm {p}}^{2} \over \omega _{\rm {p}}^{2}-\omega ^{2}}$ 2p 2 $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{\rm {p}}^{2} \over \omega _{\rm {p}}^{2}-\omega ^{2}}$ ωdisplay 2p 2 - ωdisplay2 { $displaystyle m_{\rm$ { $p} = m_{2}$ + { $m_{$ 2} \ $obega$ _ ${\rm$ { $p} } {$ 2} \ $over$ \ $m_{\rm {eff}}=m_{1}+{m_{2}\omega _{\rm {p}}^{2} \over \omega _{\rm {p}}^{2}-\omega ^{2}}$

주파수 $\omega$ (\ $displaystyle \obega)$ 가 $\omega$ 위에서 $\omega _{\rm {p}}$ p(\ $displaystyle \obega_{\rm$ { $p})$ 에 $\omega _{\rm {p}}$ 접근하면 음수입니다.플라즈마 주파수 부근에서 음질량의 영향을 이용한 메타물질들이 ^[8]^[9]보고되었다.

「」를 참조해 주세요.

전자 웨이크
플라즈마 물리학 기사 목록
플라스몬
상대론적 양자 화학
표면 플라즈몬 공명
상위 하이브리드 진동, 특히 자기장에 비스듬한 전파 각도에서 모드에 대한 수정에 대한 논의를 위해
플라즈마 물결

레퍼런스

^ Tonks, Lewi; Langmuir, Irving (1929). "Oscillations in ionized gases" (PDF). Physical Review. 33 (8): 195–210. Bibcode:1929PhRv...33..195T. doi:10.1103/PhysRev.33.195.
^ Fu, Ying (2011). Optical properties of nanostructures. Pan Stanford. p. 201.
^ *Andreev, A. A. (2000), An Introduction to Hot Laser Plasma Physics, Huntington, New York: Nova Science Publishers, Inc., ISBN 978-1-56072-803-0
^ ^a ^b Milton, Graeme W; Willis, John R (2007-03-08). "On modifications of Newton's second law and linear continuum elastodynamics". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 463 (2079): 855–880. Bibcode:2007RSPSA.463..855M. doi:10.1098/rspa.2006.1795. S2CID 122990527.
^ ^a ^b Chan, C. T.; Li, Jensen; Fung, K. H. (2006-01-01). "On extending the concept of double negativity to acoustic waves". Journal of Zhejiang University Science A. 7 (1): 24–28. doi:10.1631/jzus.2006.A0024. ISSN 1862-1775. S2CID 120899746.
^ ^a ^b Huang, H. H.; Sun, C. T.; Huang, G. L. (2009-04-01). "On the negative effective mass density in acoustic metamaterials". International Journal of Engineering Science. 47 (4): 610–617. doi:10.1016/j.ijengsci.2008.12.007. ISSN 0020-7225.
^ ^a ^b Yao, Shanshan; Zhou, Xiaoming; Hu, Gengkai (2008-04-14). "Experimental study on negative effective mass in a 1D mass–spring system". New Journal of Physics. 10 (4): 043020. Bibcode:2008NJPh...10d3020Y. doi:10.1088/1367-2630/10/4/043020. ISSN 1367-2630.
^ ^a ^b ^c Bormashenko, Edward; Legchenkova, Irina (April 2020). "Negative Effective Mass in Plasmonic Systems". Materials. 13 (8): 1890. Bibcode:2020Mate...13.1890B. doi:10.3390/ma13081890. PMC 7215794. PMID 32316640. 텍스트는 Creative Commons Attribution 4.0 International License에 따라 제공되는 이 소스로부터 복사되었습니다.
^ ^a ^b Bormashenko, Edward; Legchenkova, Irina; Frenkel, Mark (August 2020). "Negative Effective Mass in Plasmonic Systems II: Elucidating the Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation". Materials. 13 (16): 3512. Bibcode:2020Mate...13.3512B. doi:10.3390/ma13163512. PMC 7476018. PMID 32784869.

원천

Ashcroft, Neil; Mermin, N. David (1976). Solid State Physics. New York: Holt, Rinehart and Winston. ISBN 978-0-03-083993-1.

추가 정보

Longair, Malcolm S. (1998), Galaxy Formation, Berlin: Springer, ISBN 978-3-540-63785-1

[:1-2] 애쉬크로프트 & 머먼 1976, 19페이지

[1] Tonks, Lewi; Langmuir, Irving (1929). "Oscillations in ionized gases" (PDF). Physical Review. 33 (8): 195–210. Bibcode:1929PhRv...33..195T. doi:10.1103/PhysRev.33.195.

[3] Fu, Ying (2011). Optical properties of nanostructures. Pan Stanford. p. 201.

[4] *Andreev, A. A. (2000), An Introduction to Hot Laser Plasma Physics, Huntington, New York: Nova Science Publishers, Inc., ISBN 978-1-56072-803-0

[:0-5] Milton, Graeme W; Willis, John R (2007-03-08). "On modifications of Newton's second law and linear continuum elastodynamics". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 463 (2079): 855–880. Bibcode:2007RSPSA.463..855M. doi:10.1098/rspa.2006.1795. S2CID 122990527.

[:1-6] Chan, C. T.; Li, Jensen; Fung, K. H. (2006-01-01). "On extending the concept of double negativity to acoustic waves". Journal of Zhejiang University Science A. 7 (1): 24–28. doi:10.1631/jzus.2006.A0024. ISSN 1862-1775. S2CID 120899746.

[:2-7] Huang, H. H.; Sun, C. T.; Huang, G. L. (2009-04-01). "On the negative effective mass density in acoustic metamaterials". International Journal of Engineering Science. 47 (4): 610–617. doi:10.1016/j.ijengsci.2008.12.007. ISSN 0020-7225.

[:3-8] Yao, Shanshan; Zhou, Xiaoming; Hu, Gengkai (2008-04-14). "Experimental study on negative effective mass in a 1D mass–spring system". New Journal of Physics. 10 (4): 043020. Bibcode:2008NJPh...10d3020Y. doi:10.1088/1367-2630/10/4/043020. ISSN 1367-2630.

[:4-9] Bormashenko, Edward; Legchenkova, Irina (April 2020). "Negative Effective Mass in Plasmonic Systems". Materials. 13 (8): 1890. Bibcode:2020Mate...13.1890B. doi:10.3390/ma13081890. PMC 7215794. PMID 32316640. 텍스트는 Creative Commons Attribution 4.0 International License에 따라 제공되는 이 소스로부터 복사되었습니다.

[:5-10] Bormashenko, Edward; Legchenkova, Irina; Frenkel, Mark (August 2020). "Negative Effective Mass in Plasmonic Systems II: Elucidating the Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation". Materials. 13 (16): 3512. Bibcode:2020Mate...13.3512B. doi:10.3390/ma13163512. PMC 7476018. PMID 32784869.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Search

플라즈마 진동

네임스페이스

더

목차

메커니즘

'차가운' 전자

'따뜻한' 전자

플라즈마 진동 및 음질량의 영향

「」를 참조해 주세요.

레퍼런스

원천

추가 정보

Search

플라즈마 진동

메커니즘

'차가운' 전자

'따뜻한' 전자

플라즈마 진동 및 음질량의 영향

「 」를 참조해 주세요.

레퍼런스

원천

추가 정보

「」를 참조해 주세요.