삼팔면체 화합물

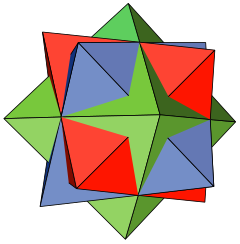
Compound of three octahedra
삼팔면체 화합물
Compound of three octahedra.svg
다면체 3 정팔면체
얼굴 24개의 정삼각형
가장자리 36
꼭지점 18
대칭군
(단색)		 오더48h

수학에서, 3개의 팔면체 또는 8면체 3개의 복합체의 화합물은 3개의 정팔면체로 이루어진 다면체 화합물이며, 모두 공통의 중심을 공유하지만 서로에 대해 회전한다.수학 문헌에는 일찍 등장했지만 1948년 그의 목판 별들의 중심 이미지에 그것을 사용한 M. C. 에셔에 의해 재발견되고 대중화 되었다.

건설

정팔면체는 정육면체의 2개의 반대되는 정사각형의 8개의 가장자리가 정팔면체의 8개 면에 놓이도록 정육면체 주위에 외접할 수 있다.세 쌍의 정육면체로부터 이렇게 형성된 세 개의 팔면체는 세 개의 [1]팔면체의 화합물을 형성한다.8개의 입방체 정점은 3개의 모서리가 [2]서로 교차하는 화합물 내 8개의 점과 동일합니다.이러한 3중 교차에 관여하는 각 8면체의 가장자리는 1:22의 [2]교점 비율로 나누어져 있다.나머지 8면체 모서리는 컴파운드 내부에서 쌍으로 교차하며 교차점은 중간점에 있으며 직각을 형성합니다.

3개의 팔면체의 합성물은 또한 시작 팔면체의 [3]두 개의 반대 정점을 통과하는 세 개의 대칭 축 중 하나를 중심으로 각 복사본을 θ/4의 각도로 회전시킴으로써 단일 팔면체의 세 개의 복사본에서 형성될 수 있다.3개의 8면체의 동일한 화합물에 대한 세 번째 구조는 균일한 다면체 화합물 중 하나인 3개의 입방체 화합물의 이중 다면체이다.

3개의 팔면체 중 하나의 꼭지점 6개는 좌표(0, 0, ±2)와 (±,2, ±,2, 0)로 나타낼 수 있다.다른 두 개의 8면체에는 이러한 좌표에서 z 좌표를 [1][2]x 또는 y 좌표로 교환하여 얻을 수 있는 좌표가 있습니다.

대칭

에셔의 별과 폭포 연구에 사용된 세 개의 평평한 팔면체의 합성물인 스텔레이트 마름모꼴 12면체.

세 팔면체의 화합물은 단일 팔면체와 동일한 대칭군을 가진다.그것은 면은 등변삼각형이고 모든 면을 다른 면으로 향하게 하는 대칭을 가지고 있다는 것을 의미하는 등면체이다.알려진 한 개의 무한 동면체 델타헤드라 패밀리가 있고, 이 패밀리에 속하지 않는 36개가 더 있습니다. 3개의 팔면체의 화합물은 36개의 산발적인 [4]예 중 하나입니다.그러나 대칭군이 모든 정점을 다른 정점으로 가져가는 것은 아니기 때문에 그 자체가 균일한 다면체 화합물은 아니다.

3개의 팔면체의 교점은 볼록 다면체로, 14개의 꼭지점과 24개의 면, 즉 사각형 피라미드를 중앙 [2]입방체의 각 면에 붙여 형성한 6면체이다.따라서 이 화합물은 4면체 육면체의 스테어링으로 볼 수 있다.입방체의 각 면에 더 높은 피라미드를 사용하여 형성된 다른 형태의 4면체 6면체는 비볼록형이지만, 3개의 팔면체의 면과 같은 면에 다시 놓여 있는 등변 삼각형 면을 가지고 있다. 이는 알려진 또 다른 이등면체 델타면체 중 하나이다.6개의 사면체 화합물인 동일한 면면을 공유하는 제3의 동면체 다면체는 3개의 팔면체 화합물의 각 면을 3개의 팔면체(팔면체)를 형성하여 형성할 수 있다.3개의 8면체 화합물의 계단식이기도 한, 같은 면면을 가지는 제4의 동면체 다면체는, 4면체와 같은 조합 구조를 가지지만,[4] 입방체의 외부에 피라미드를 붙이는 대신에, 입방체의 면이 안쪽으로 찌그러져 교차하는 피라미드로 되어 있다.

3개의 팔면체를 포함할 수 있는 입방체는 9개의 반사 대칭면을 가지고 있다.이러한 반사 창 중 3개는 반대편 2개의 면 중간에서 큐브의 면과 평행하게 통과하고 나머지 6개는 큐브의 정점 4개를 대각선으로 통과합니다.이 9개의 평면은 3개의 [2]8면체의 9개의 적도면과 일치한다.

역사

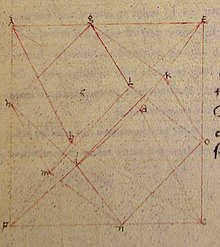
피에로 델라 프란체스카가 그의 책 De quinque corpus regularbus를 위해 그린 입방체 주위에 둘러싸인 8면체

피에로 델라 프란체스카가 쓴 15세기 사본 De quinque corpinibus regularbus에서 델라 프란체스카는 이미 정육면체 주위에 둘러싸인 8개의 정육면체 모서리가 8개의 면에 놓여 있는 8개의 정육면체의 그림을 포함하고 있다.하나의 입방체 주위에 이러한 방식으로 둘러싸인 세 개의 팔면체는 세 개의 팔면체의 화합물을 형성하지만, 델라 프란체스카는 그 [5]화합물을 묘사하지 않는다.

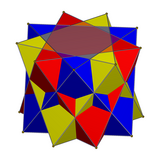
수학 문헌에서 3개의 8면체의 화합물의 다음 출현은 막스 브루크너의 1900년 작품인 것으로 보이며, 이 작품에는 그것을 언급하고 그것의 [2][6]모형 사진이 포함되어 있다.

네덜란드 예술가 M. C. 에셔는 1948년 자신의 목판 별에서 두 개의 카멜레온이 들어 있고 우주를 [7]떠다니는 이 모양의 새장을 나무 조각의 중심 인물로 사용했습니다.H. S. M. 콕서터는 에셔가 독립적으로 이 형상을 재발견했다고 가정하고, "대수나 해석 기하학에 대한 지식 없이 에셔가 이 매우 대칭적인 [2]도형을 재발견할 수 있었다는 것은 주목할 만한 일이다."라고 쓰고 있다.하지만, 조지 W. 하트는 에셔가 브루크너의 작품을 잘 알고 있었고 그가 [8]그린 많은 다면체와 다면체 화합물의 기초로 그것을 사용했다고 기록했습니다.앞서 1948년, 에셔는 비슷한 주제인 Study for Stars를 가지고 예비 목판을 만들었지만, 연구에서 세 개의 정팔면체의 화합물을 사용하는 대신 그는 세 개의 평탄한 [9]팔면체의 화합물로 형성될 수 있는 다른 하지만 관련된 형태인 스테로이드 마름모꼴 십이면체를 사용했습니다.다면체로서의 이 형태는 위상적으로 마름모꼴 면에 더 짧은 피라미드가 있는 마름모꼴 12면체로 볼 수 있는 디디아키스 12면체와 동일하다.세 개의 입방체의 화합물인 팔면체 화합물의 이중 모양은 같은 스텔레이트 마름모꼴 12면체 [7]옆에 있는 나중에 나온 에셔 목판인 폭포에도 나타나 있습니다.

3개의 8면체의 화합물은 그 존재를 관찰하고 정점에 좌표를 제공한 바코스 & 존슨(1959)의 작업으로 수학 문헌에 더 적절하게 재진입했다.그것은 Wenninger와 Coxeter에 의해 더 자세히 연구되었다.

3개의 팔면체의 기타 화합물

팔면체를 삼각형 대향으로 볼 때, D대칭의 또3d 다른 균일한 반향 프리즘 화합물이 존재한다.순서 12.각 안티프리즘은 40도 회전한다.상단 및 하단 평면에 복합 Enneagram {9/3} 또는 3{3}이(가) 포함되어 있는 것을 볼 수 있습니다.

Compound three triangular antiprisms.png

「 」를 참조해 주세요.

레퍼런스

  1. ^ a b 를 클릭합니다Bakos, T.; Johnson, Norman W. (1959), "Octahedra inscribed in a cube", The Mathematical Gazette, 43 (343): 17–20, JSTOR 3608867.
  2. ^ a b c d e f g 3개의 팔면체 화합물에 대한 논의는 페이지 61~62에 있다Coxeter, H. S. M. (1985), "A special book review: M. C. Escher: His life and complete graphic work", The Mathematical Intelligencer, 7 (1): 59–69, doi:10.1007/BF03023010.
  3. ^ 를 클릭합니다Wenninger, M. J. (1968), "Some interesting octahedral compounds", The Mathematical Gazette, 52 (379): 16–23, JSTOR 3614454.
  4. ^ a b 를 클릭합니다Shephard, G. C. (1999), "Isohedral deltahedra", Periodica Mathematica Hungarica, 39 (1–3): 83–106, doi:10.1023/A:1004838806529.
  5. ^ 를 클릭합니다Hart, George W. (1998), "Piero della Francesca's Polyhedra", Virtual Polyhedra.
  6. ^ 콕서터(1985년)가 인용한 바와 같이Brückner, Max (1900), Vielecke und Vielflache, Leipzig: Teubner, p. 188 and Tafel VIII 12.
  7. ^ a b 를 클릭합니다Hart, George W. (1996), "The Polyhedra of M.C. Escher", Virtual Polyhedra.
  8. ^ Hart, George W., "Max Brücknerʼs Wunderkammer of Paper Polyhedra", Bridges 2019 Conference Proceedings (PDF), pp. 59–66
  9. ^ 제노바 대학의 리비오 제피로(Livio Zefiro)라는 세 개의 팔면체와 세 개의 정사각형 다이프라미드의 주목할 만한 화합물.

외부 링크