패리티(물리학)

양자역학에서 패리티 변환(패리티 반전이라고도 함)은 하나의 공간 좌표 부호의 반전입니다.3차원에서는 3개의 공간 좌표(점 반사)를 모두 동시에 플립하는 것을 나타낼 수도 있습니다.

\mathbf {P} : {\begin{pmatrix}x\y\end{pmatrix}}\map to {\begin{pmatrix}-x\-y\-z\end{pmatrix}}}.

또한 패리티 반전이 현상을 거울 이미지로 변환한다는 점에서 물리적 현상의 키라리티를 테스트하는 것으로도 생각할 수 있습니다.약한 상호작용을 제외하고 기본 입자의 모든 기본 상호작용은 패리티 하에서는 대칭입니다.약한 상호작용은 키랄성이므로 물리에서 키랄성을 탐색하는 수단을 제공합니다.원자 및 분자 물리학의 전자기학과 같이 패리티 아래에서 대칭인 상호작용에서 패리티는 양자 전이의 기초가 되는 강력한 제어 원리로 작용합니다.

P의 행렬 표현은 (임의의 차원수에서) -1과 같은 행렬식을 가지며, 따라서 1과 같은 행렬식을 갖는 회전과 구별된다.2차원 평면에서 부호의 모든 좌표를 동시에 플립하는 것은 패리티 변환이 아니라 180° 회전과 동일합니다.

양자역학에서 패리티 변환에 의해 변하지 않는 파동함수는 짝수함수로 기술되는 반면 패리티 변환에 의해 부호가 변화하는 파동함수는 홀수함수로 기술된다.

단순 대칭 관계

회전 하에서 고전적인 기하학적 객체는 높은 등급의 스칼라, 벡터 및 텐서로 분류할 수 있습니다.고전 물리학에서 물리적 구성은 모든 대칭 그룹의 표현 하에 변환되어야 합니다.

양자 이론은 힐베르트 공간의 상태가 회전 그룹의 표현 아래에서는 변환될 필요가 없고 투영 표현 아래에서만 변환될 것이라고 예측합니다.투영이라는 단어는 양자 상태의 전체 위상이 관측할 수 없다는 것을 상기시키는 각 상태의 위상을 투영하면 투영 표현은 일반 표현으로 감소한다는 사실을 말한다.모든 표현도 투영 표현이지만, 그 반대가 참이 아니기 때문에 양자 상태의 투영 표현 조건은 고전 상태의 표현 조건보다 약하다.

모든 그룹의 투영 표현은 그룹의 중앙 확장에 대한 일반적인 표현과 동일하다.예를 들어 특수 직교군 SO(3)인 3차원 회전군의 투영 표현은 특수 유니터리군 SU(2)의 통상 표현이다.표현이 아닌 회전군의 투영 표현은 스피너라고 불리며, 따라서 양자 상태는 텐서뿐만 아니라 스피너로도 변환될 수 있습니다.

여기에 패리티에 의한 분류를 추가하면 예를 들어 다음과 같은 개념으로 확장될 수 있습니다.

회전 불변인 스칼라(P = +1) 및 의사 스칼라(P = -1)입니다.
회전 중인 벡터로 변환되는 벡터(P = -1) 및 축 벡터(일명 의사 벡터)(P = +1)입니다.

다음과 같은 반사를 정의할 수 있습니다.

{displaystyle V_{x}:\begin{pmatrix}x\y\end{pmatrix}\map to {begin{pmatrix}-x\y\end{pmatrix}}},

또한 음의 결정 인자를 가지며 유효한 패리티 변환을 형성합니다.그런 다음 회전(또는 x, y 및 z 반사를 연속적으로 수행)과 결합하면 앞서 정의한 특정 패리티 변환을 복구할 수 있습니다.단, 첫 번째 패리티 변환은 양의 결정 요인이 되기 때문에 짝수 차원에서는 작동하지 않습니다.짝수 차원에서는 패리티 변환(또는 홀수 좌표의 반사)의 후자 예만 사용할 수 있습니다.

패리티는 P ${\hat {\mathcal {P}}}^{2}={\hat {1}}$ ^ ${\hat {\mathcal {P}}}^{2}={\hat {1}}$ ${\hat {\mathcal {P}}}^{2}={\hat {1}}$ $^$ { $displaystyle$ \ $mathbb {$ Z } _ { $2$ } ^{ displaystyle \ $mathcal$ { $P}$ ^{2} = $hat {1$ } ${\hat {\mathcal {P}}}^{2}={\hat {1}}$ } ${\hat {\mathcal {P}}}^{2}={\hat {1}}$ 로 인해 아벨 $\mathbb {Z} _{2}$ Z $\mathbb {Z} _{2}$ {\ $displaystyle$ \ mathbbb {Z} _ {2} _{2}을 $\mathbb {Z} _{2}$ 형성합니다. 모든 아벨 그룹에는 1차원적인 표현만 있습니다. $(\$ $displaystyle$ $\mathbb {Z} _{2$ 에는 2개의 축소할 수 없는 표현이 있습니다.하나는 짝수 ${\hat {\mathcal {P}}}\phi =+\phi$ 인 ${\hat {\mathcal {P}}}\phi =+\phi$ ${\hat {\mathcal {P}}}\phi =-\phi$ ^ ${\hat {\mathcal {P}}}\phi =+\phi$ + $(\displaystyle$ { $p$ $})$ 이고, 다른 하나는 ${\hat {\mathcal {P}}}\phi =-\phi$ 인 ${\hat {\mathcal {P}}}\phi =-\phi$ P ^ ${\hat {\mathcal {P}}}\phi =+\phi$ ${\hat {\mathcal {P}}}\phi =-\phi$ + \ $phi$ $}$ 입니다.단, 아래에서 자세히 설명한 바와 같이 양자역학 상태에서는 실제 패리티 표현 하에서만 변환될 필요가 없으며 투영 표현 하에서만 변환될 수 있으므로 원칙적으로 패리티 변환은 어떤 위상으로든 상태를 회전시킬 수 있습니다.

O(3)의 표현

위의 스칼라, 의사 스칼라, 벡터 및 의사 벡터의 분류를 작성하는 대체 방법은 각 객체가 변환하는 표현 공간입니다.이는 표현을 정의하는 군 동형사상 $\rho$ {\(\ $displaystyle\rho)$ 의 $\rho$ 관점에서 나타낼 수 있다. $R\in {\text{O}}(3),$ R $R\in {\text{O}}(3),$ $R\in {\text{O}}(3),$ ( $R\in {\text{O}}(3),$ 3 )의 경우 $,$ \ $displaystyle$ R $\in\text{$ $O}}(3),}$

$\rho (R)=1$ : $\rho (R)=1$ ( $\rho (R)=1$ ) $\rho (R)=1$ $\rho (R)=1$ ( \ $displaystyle \rho$ ( $\rho (R)=1$ R ) $= 1$ , trivial 표현
$\rho (R)=\det(R)$ : $\rho (R)=\det(R)$ ( $\rho (R)=\det(R)$ ) $\rho (R)=\det(R)$ ( $\rho (R)=\det(R)$ $displaystyle \rho$ ( $R)$ = \ $det$ ( $R$ ) }
$\rho (R)=R$ : $\rho (R)=R$ ( $\rho (R)=R$ ) $=$ {\ $displaystyle \rho (R$ )= $R$ 기본 표현
$\rho (R)=\det(R)R.$ 벡터: " $\rho (R)=\det(R)R.$ " ( $\rho (R)=\det(R)R.$ ) $\rho (R)=\det(R)R.$ ( $\rho (R)=\det(R)R.$ ) $\rho (R)=\det(R)R.$ . $\rho (R)=\det(R)R.$ { $displaystyle \rho (R$ ) = \ $det (R) R$ }

SO ${\text{SO}}(3)$ ( $)\$ $displaystyle\$ text { }로 ${\text{SO}}(3)$ 이 제한되는 경우 $SO}}(3$ 스칼라 및 의사벡터와 마찬가지로 스칼라와 의사벡터가 동일하게 변환됩니다.

고전 역학

뉴턴의 $\mathbf {F} =m\mathbf {a}$ 방정식 F $\mathbf {F} =m\mathbf {a}$ $\mathbf {F} =m\mathbf {a}$ $\mathbf {F} =m\mathbf {a}$ \ $displaystyle \mathbf {F} =m\mathbf {a} }$ (질량이 일정할 경우)는 두 벡터와 같으므로 패리티 하에서는 불변이다.또한 중력의 법칙은 벡터만을 포함하며, 따라서 패리티 하에서는 불변합니다.

단, $\mathbf {L}$ L(\ $displaystyle \mathbf {L})$ 은 $\mathbf {L}$ 축방향 벡터이다.

\displaystyle {\mathbf {L} &=\mathbf {r} \times \mathbf {p} \{\hat {P}} \left(\mathbf {L} \right)&=times(\mathbf {p})=\mathbf {L} \end}.aligned}

고전 전기역학에서 $(\displaystyle \rho)$ 는 $\rho$ 스칼라, 전계 $(\$ 및 $\mathbf {j}$ j(\ $displaystyle \mathbf {j})$ 는 $\mathbf {j}$ 벡터이지만 자기장 $(\$ 는 $\mathbf {B}$ 축 벡터이다.그러나 Maxwell의 방정식은 축 벡터의 컬이 벡터이기 때문에 패리티 하에서는 불변합니다.

고전 물리학의 일부 변수에 대한 공간 반전의 영향

고전적인 물리적 변수의 두 주요 분할은 짝수 또는 홀수 패리티를 가집니다.특정 변수와 벡터가 어느 하나의 범주로 분류되는 방법은 공간의 차원이 홀수인지 짝수인지에 따라 달라집니다.패리티 변환에 대해 홀수 또는 아래에 제시된 범주는 다르지만 밀접하게 관련된 문제입니다.

아래 답변은 3차원 공간에 대한 정답입니다.예를 들어, 2차원 공간에서는 행성의 표면에 머무르도록 구속되면 일부 변수가 변을 바꾼다.

이상한

공간 반전 시 부호가 뒤집히는 고전 변수는 주로 벡터입니다.다음과 같은 것이 있습니다.

$\displaystyle$ h $h$ 헬리시티
$φ \$ $displaystyle$ \ $\Phi$ Phi $\Phi$ , 자속
$(\$ 3공간 내 입자의 위치
$\mathbf {v}$ $\$ 입자 속도
$\$ displaystyle $\mathbf {a$
$\$ 입자의 선형 운동량
$§$ $v\displaystyle$ \rho $,\mathbf$ {v $\rho \,\mathbf {v}$ $\rho \,\mathbf {v}$ ^[a]
$(\$ \ $mathbf$ {F $\mathbf {F}$ 입자에 가해지는 힘
$\mathbf {J}$ J $(\displaystyle$ \ $mathbf$ {J $\mathbf {J}$ 전류 밀도
$(\displaystyle$ \ $mathbf$ {E $\mathbf {E}$ 전계
$(\displaystyle$ \ $mathbf$ {D $\mathbf {D}$ 전기 변위 필드
$\$ 전기 편파
$(\$ 전자 벡터 퍼텐셜
$\mathbf {S}$ S $\mathbf {S}$ \ $displaystyle \mathbf {S$ 포인팅 벡터(전자파워의 흐름).

심지어.

공간 반전에 따라 변경되지 않는 고전적 변수(주로 스칼라 양)는 다음과 같습니다.

$\displaystyle$ t $t$ 이벤트가 발생한 시각
$\displaystyle$ m $m$ 입자의 질량
$(\displaystyle$ E $E$ 입자의 에너지
$P$ $\$ $displaystyle$ P $P$ 전원 (작업속도)
$§$ $(\displaystyle$ \rho $\rho$ 전하 밀도
$(\displaystyle$ V $V$ 스칼라 전위(전압)
$§$ $(\displaystyle$ \rho $\rho$ 전자기장의 에너지 밀도
$\mathbf {L}$ \ $displaystyle \mathbf {L$ 입자의 각운동량(궤도와 스핀 모두)(축 벡터)
$(\$ 자기장(축 벡터)
$(\$ 보조 자기장
$(\displaystyle$ \ $mathbf$ {M $\mathbf {M}$ 자화
$T_{ij}$ j $($ T_ ${ij$ Maxwell 응력 텐서.
약한 힘과 관련된 것을 제외한 모든 질량, 전하, 결합 상수 및 기타 스칼라 물리 상수.

양자역학

가능한 고유값

패리티의 2차원 표현은 패리티 하에서 서로 맞물리는 양자 상태의 쌍에 의해 주어진다.단, 이 표현은 항상 상태의 선형 조합으로 축소할 수 있습니다.각 조합은 짝수 또는 홀수 언더 패리티입니다.누군가는 모든 축소할 수 없는 패리티의 표현은 일차원적이라고 말한다.

양자역학에서 시공간 변환은 양자 상태에 작용한다.패리티 변환 $^(\$ {P ${\hat {\mathcal {P}}}$ 은 일반적으로 $\psi$ {\(\ $displaystyle \psi)$ 에 $\psi$ 작용하는 단일 연산자입니다. ${\hat {\mathcal {P}}}\,\psi {\left(r\right)}=e^{{i\phi }/{2}}\psi {\left(-r\right)}$ ^ ${\hat {\mathcal {P}}}\,\psi {\left(r\right)}=e^{{i\phi }/{2}}\psi {\left(-r\right)}$ ^ （ ${\hat {\mathcal {P}}}\,\psi {\left(r\right)}=e^{{i\phi }/{2}}\psi {\left(-r\right)}$ ） ${\hat {\mathcal {P}}}\,\psi {\left(r\right)}=e^{{i\phi }/{2}}\psi {\left(-r\right)}$ ${\hat {\mathcal {P}}}\,\psi {\left(r\right)}=e^{{i\phi }/{2}}\psi {\left(-r\right)}$ ${\hat {\mathcal {P}}}\,\psi {\left(r\right)}=e^{{i\phi }/{2}}\psi {\left(-r\right)}$ / 2 ${\hat {\mathcal {P}}}\,\psi {\left(r\right)}=e^{{i\phi }/{2}}\psi {\left(-r\right)}$ - $r$ 、 \ $display style \ mathcal {$ P } 、 \ $psi （ r ）$ $}=e^{i$ \phi $}/{2}}\psi(왼쪽$

${\hat {\mathcal {P}}}^{2}\,\psi {\left(r\right)}=e^{i\phi }\psi {\left(r\right)}$ ^ ${\hat {\mathcal {P}}}^{2}\,\psi {\left(r\right)}=e^{i\phi }\psi {\left(r\right)}$ ( ( ${\hat {\mathcal {P}}}^{2}\,\psi {\left(r\right)}=e^{i\phi }\psi {\left(r\right)}$ ) ${\hat {\mathcal {P}}}^{2}\,\psi {\left(r\right)}=e^{i\phi }\psi {\left(r\right)}$ ${\hat {\mathcal {P}}}^{2}\,\psi {\left(r\right)}=e^{i\phi }\psi {\left(r\right)}$ ${\hat {\mathcal {P}}}^{2}\,\psi {\left(r\right)}=e^{i\phi }\psi {\left(r\right)}$ ${\hat {\mathcal {P}}}^{2}\,\psi {\left(r\right)}=e^{i\phi }\psi {\left(r\right)}$ ( ${\hat {\mathcal {P}}}^{2}\,\psi {\left(r\right)}=e^{i\phi }\psi {\left(r\right)}$ ){ $displaystyle$ {\ $mathcal {P}^{2},\psi(r\right)가$ 있어야 합니다 $.$ $}=e^{i\phi }\psi {left($ r ${\hat {\mathcal {P}}}^{2}\,\psi {\left(r\right)}=e^{i\phi }\psi {\left(r\right)}$ right)}}. 전체 위상은 관측할 수 없기 때문에.한 ${\hat {\mathcal {P}}}^{2}$ 의 ${\hat {\mathcal {P}}}^{2}$ 를 두 번 반전시키는 연산자 P ${\hat {\mathcal {P}}}^{2}$ ^ $2({$ 는 시공간 불변성을 유지하며, 단계 $e^{i\phi }$ †({ $displaystyle$ e $^{i\phi$ ${\hat {\mathcal {P}}}^{2}$ 로 고유 ${\hat {\mathcal {P}}}^{2}$ 를 회전시키는 내부 대칭도 $마찬가지입니다.$ 만약 P $^2({$ displaystyle {\hatyle {\mathcal { $P}^}$ } ${\hat {\mathcal {P}}}^{2}$ } }^2 $}$ } } ^2 ^2 ${\hat {\mathcal {P}}}^{2}$ } } } ^2 } ^2 } }위상 회전의 연속 U(1) 대칭 그룹의 $e^{iQ}$ $e^{iQ}$ $e^{iQ}$ {\ $displaystyle$ e $^{iQ},$ e $e^{iQ}$ $e^{-iQ}$ - $e^{-iQ}$ i $e^{-iQ}$ ${\$ e $^{-iQ}}$ 는 $e^{-iQ}$ 이 U(1)의 일부이며 대칭이기도 하다.특히 P ${\hat {\mathcal {P}}}'\equiv {\hat {\mathcal {P}}}\,e^{-{iQ}/{2}}$ ^ ${\hat {\mathcal {P}}}'\equiv {\hat {\mathcal {P}}}\,e^{-{iQ}/{2}}$ ${\hat {\mathcal {P}}}'\equiv {\hat {\mathcal {P}}}\,e^{-{iQ}/{2}}$ - i ${\hat {\mathcal {P}}}'\equiv {\hat {\mathcal {P}}}\,e^{-{iQ}/{2}}$ / ${\hat {\mathcal {P}}}'\equiv {\hat {\mathcal {P}}}\,e^{-{iQ}/{2}}$ (\ $displaystyle {\mathcal {P}}, e^$ {- $iQ}/{2$ 를 ${\hat {\mathcal {P}}}'\equiv {\hat {\mathcal {P}}}\,e^{-{iQ}/{2}}$ 할 수 있으므로 P ${\hat {\mathcal {P}}}'$ ^ ${\hat {\mathcal {P}}}'$ $display$ style { $p}을($ 를) 호출할 수 $.$ $aystyle {\mathcal {P$ P ${{\hat {\mathcal {P}}}'}^{2}=1$ ^ ${{\hat {\mathcal {P}}}'}^{2}=1$ ${{\hat {\mathcal {P}}}'}^{2}=1$ 2 $=$ { $style {\$ $hat$ ${P}}^{2}=1$ }이므로 ${{\hat {\mathcal {P}}}'}^{2}=1$ P ${\hat {\mathcal {P}}}'$ ^ ^ ${\hat {\mathcal {P}}}'$ ^ ^ ${\$ {\ $displaystyle {\$ $mathcal$ ${P$ $\pm 1$ 의 ${\hat {\mathcal {P}}}'$ 고유값은 $\pm 1$ ± $1$ 이지만 패리티 변환에서는 +1인 파형 함수는 짝수입니다.-1은 홀수 ^[1]함수에 해당합니다.그러나 이러한 대칭 그룹이 존재하지 않는 경우 모든 패리티 $\pm 1$ 에 ± $\pm 1$ 1 $\displaystyle$ \ $pm$ 1 이외의 $\pm 1$ 위상이 있는 고유값이 있을 수 있습니다.

전자파 함수의 경우, 짝수 상태는 보통 gerade(독일어: 짝수)의 첨자 g와 ungerade(독일어: 홀수)의 첨자 u로 표시됩니다.예를 들어 수소 분자 이온(H₂⁺)의 최저 에너지 레벨은 1 $µg {$ 1 $\sigma$ _ ${g}$ 로 $1\sigma _{g}$ 표시되고 다음으로 가까운(높은) 에너지 레벨은 $1\sigma _{u}$ µu { $displaystyle 1\sigma _{$ u $1\sigma _{u}$ ^[2]로 $1\sigma _{u}$ 됩니다.

외부 전위로 이동하는 입자의 파동 함수는, 중심대칭(공간 반전에 대해 불변하고 원점에 대칭인 위치 에너지 불변)이거나 변화 부호입니다. 이 두 가지 가능한 상태를 파동 ^[3]함수의 짝수 상태 또는 홀수 상태라고 합니다.

입자의 패리티 보존의 법칙(^[4]핵의 베타 붕괴에 대해 참이 아님)은 입자의 고립된 앙상블이 확실한 패리티를 가지면, 그 패리티는 앙상블 진화 과정에서 불변하게 유지된다고 기술한다.

구대칭 외부 장에서 이동하는 입자 상태의 패리티는 각 운동량에 의해 결정되며, 입자 상태는 총 에너지, 각 운동량 및 각 ^[3]운동량의 투영이라는 세 가지 양자 수로 정의됩니다.

패리티 대칭의 결과

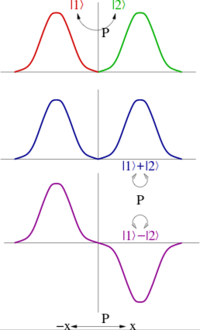
패리티가 Abelian 그룹₂ δ를 생성할 때 항상 양자 상태의 선형 조합을 취할 수 있으며, 짝수 또는 홀수 패리티 아래에 있습니다(그림 참조).따라서 이러한 상태의 패리티는 ±1입니다.다중 입자 상태의 패리티는 각 상태의 패리티의 곱입니다. 즉, 패리티는 곱셈 양자수입니다.

양자역학에서 P $^$ {\ $mathcal$ {P $}}}$ 이 ${\hat {\mathcal {P}}}$ (가) 해밀턴과 교호작용하는 ${\hat {\mathcal {P}}}$ 패리티 변환에서는 해밀턴이 불변(대칭)합니다.비이론적인 양자역학에서는 V $V=V{\left(r\right)}$ ( $V=V{\left(r\right)}$ r ) = $V$ { \ $left$ ( $r$ \ $right$ ) $V=V{\left(r\right)}$ 과 $V=V{\left(r\right)}$ 스칼라 전위에 대해 이러한 현상이 발생하므로 전위는 구면적으로 대칭이다.다음과 같은 사실을 쉽게 입증할 수 있습니다.

$\left|\varphi \right\rangle$ { $displaystyle$ \ $\left|\psi \right\rangle$ $left$ $\left|\psi \right\rangle$ \ $varphi \ right$ \ $rangle$ } $\left|\psi \right\rangle$ ${\$ $display$ 、 $\left\langle \varphi \left|{\hat {X}}\right|\psi \right\rangle =0$ X $\left\langle \varphi \left|{\hat {X}}\right|\psi \right\rangle =0$ ^ ^ $\left\langle \varphi \left|{\hat {X}}\right|\psi \right\rangle =0$ 0 \ $displaystyle$ \ left \ $varphi$ \ $left$ \ $hat$ { $X}$ \ $right \ rangle$ $=$ 0 \ displaystyle ${\hat {X}}$ 。 ${\hat {X}}$ 서 $\left\langle \varphi \left|{\hat {X}}\right|\psi \right\rangle =0$ , \ displaystyle \ wright \ varphi \ right \ rangle x ${\}}$ x x x x x x x if if if if if if if if if if if \ par {\ if if x x.
$\left|{\vec {L}},L_{z}\right\rangle$ L $\left|{\vec {L}},L_{z}\right\rangle$ 의 경우, L $\left|{\vec {L}},L_{z}\right\rangle$ ${\$ {\ $displaystyle \left \vec$ { $L$ $}},$ L_ ${z}\right\rangle }$ 의 $\left|{\vec {L}},L_{z}\right\rangle$ 궤도 ${\vec {L}}$ L $L_{z}$ $→$ {\ $display\style$ ${z$ ${\hat {\mathcal {P}}}\left|{\vec {L}},L_{z}\right\rangle =\left(-1\right)^{L}\left|{\vec {L}},L_{z}\right\rangle$ ^ L ${\hat {\mathcal {P}}}\left|{\vec {L}},L_{z}\right\rangle =\left(-1\right)^{L}\left|{\vec {L}},L_{z}\right\rangle$ , ${\hat {\mathcal {P}}}\left|{\vec {L}},L_{z}\right\rangle =\left(-1\right)^{L}\left|{\vec {L}},L_{z}\right\rangle$ - ${\hat {\mathcal {P}}}\left|{\vec {L}},L_{z}\right\rangle =\left(-1\right)^{L}\left|{\vec {L}},L_{z}\right\rangle$ ${\hat {\mathcal {P}}}\left|{\vec {L}},L_{z}\right\rangle =\left(-1\right)^{L}\left|{\vec {L}},L_{z}\right\rangle$ ${\hat {\mathcal {P}}}\left|{\vec {L}},L_{z}\right\rangle =\left(-1\right)^{L}\left|{\vec {L}},L_{z}\right\rangle$ ${\hat {P}}\left {vec {L}}, L_{z}\right\rangle =\left(왼쪽) 1\right($ $L}\left{vec$ { $L}, L_{z}\right\rangle$ ${\hat {\mathcal {P}}}\left|{\vec {L}},L_{z}\right\rangle =\left(-1\right)^{L}\left|{\vec {L}},L_{z}\right\rangle$
[ $\left[{\hat {H}},{\hat {P}}\right]=0$ , $\left[{\hat {H}},{\hat {P}}\right]=0$ ] $=$ \ $displaystyle \left$ [ { \ $hat$ { $H$ } , { \ $hat$ { $P$ } \ $right$ ]= $0$ 인 $\left[{\hat {H}},{\hat {P}}\right]=0$ 경우 원자 쌍극자 천이는 반대 ^[5]패리티의 상태 사이에서만 발생합니다.
[ $\left[{\hat {H}},{\hat {P}}\right]=0$ , $\left[{\hat {H}},{\hat {P}}\right]=0$ ] $\left[{\hat {H}},{\hat {P}}\right]=0$ { $displaystyle \left$ [ { \ $hat$ { $H$ } , { \ $hat$ { $P$ } \ $right$ } = $0$ }인 ${\hat {H}}$ 경우 ${\hat {H}}$ H ${\hat {H}}$ ^ ^ 의 ${\hat {H}}$ 고유 상태는 패리티 연산자의 고유 상태이기도 합니다. 즉, H $^$ { H } style { $H$ ${\hat {H}}$ } } ^ } ${\hat {H}}$ } ^ style의 비퇴화 고유 함수입니다. ${\mathcal {P}}$ 또는 ${\hat {\mathcal {P}}}$ P $^$ {\ $displaystyle {\mathcal {P$ 에 ${\hat {\mathcal {P}}}$ 부호가 변경됩니다.

H $^(\$ {H $})$ 의 ${\hat {H}}$ 비퇴화 고유함수 중 ${\hat {\mathcal {P}}}$ 는 ${\hat {\mathcal {P}}}$ 패리티 P ^(\displaystyle $\hat\mathcal {P}})$ 의 ${\hat {\mathcal {P}}}$ 영향을 받지 않으며, 다른 함수는 해밀턴 연산자와 패리티 연산자가 이동할 때 부호만 반전됩니다.

(\displaystyle \hat {P}\left \psi \right\rangle = c\left \psi \right\rangle , )

$c$ 서c {\ $displaystyle$ c}는 $c$ P $^$ {\ $displaystyle {P$ 의 고유값인 상수입니다.

\displaystyle \hat {P}^{2}\left \psi \right\rangle = c, {\hat {P}\left \psi \right\rangle .}

다입자계: 원자, 분자, 핵

다입자계의 전체적인 패리티는 1입자 상태의 패리티의 산물이다.홀수 입자가 홀수 패리티 상태이면 -1이고 홀수 패리티 상태이면 +1입니다.핵, 원자 및 분자의 패리티를 나타내기 위해 다른 표기법이 사용됩니다.

원자

원자 궤도는 패리티(-1)^ℓ를 가지며, 여기서 지수 θ는 방위 양자수이다.이 패리티는 θ = 1, 3, ...인 궤도 p, f, ...에 대해 홀수이고, 홀수 개수의 전자가 이러한 궤도를 차지하면 원자 상태는 홀수 패리티를 가집니다.예를 들어 질소원자의 지반상태는 전자구성 1s2s2p를²²³ 가지며, 전기항심볼^o S로 식별되며, 전기상자 o는 홀수패리티를 나타낸다.그러나 지상 약 83,300cm의⁻¹ 세 번째 들뜸항은 전자구성 1s2s2p3s는²²² 2p 전자가 2개밖에 없기 때문에 짝수 패리티를 가지며, 그 조건 기호는 P(o ^[6]슈퍼스크립트 없음)이다.

분자

모든 분자의 완전(회전-진동-전자-핵 스핀) 전자 해밀턴은 패리티 연산 P(또는 Longuet-Higgins에^[7] 의해 도입된 표기법에서는 E*)와 정합(또는 불변)하며, 그 고유치는 각각 짝수 또는 홀수인 패리티 대칭 라벨 + 또는 -를 부여할 수 있다.패리티 연산은 질량의 분자 중심에서 전자 및 핵 공간 좌표의 반전을 포함한다.

평형 상태의 중심대칭 분자는 중간점(핵질량의 중심)에 대칭의 중심이 있다.여기에는 에틸렌, 벤젠, 사불화 제논, 육불화 황과 같은 특정 대칭 분자와 모든 동핵 이원자 분자가 포함됩니다.중심대칭 분자의 경우 점군은 패리티 연산과 혼동해서는 안 되는 연산 i를 포함한다.연산 i는 핵질량 중심에서의 전자 및 진동 변위 좌표의 반전을 포함한다.중심대칭 분자의 경우 연산 i가 로비브론(회전-진동-전자) 해밀턴과 통신하며 이러한 상태에 레이블을 붙이는 데 사용할 수 있습니다.중심대칭 분자의 전자 및 진동 상태는 연산 i에 의해 변화하거나 부호 i에 의해 변화한다.전자는 첨자 g로 표시되며 gerade라고 불리며, 후자는 첨자 u로 표시되며 ^[8]ungerade라고 불립니다.중심대칭 분자의 완전한 해밀토니안은 핵 초미세 해밀토니안의 효과 때문에 점군 반전 연산 i와 이동하지 않는다.핵 초미세 Hamiltonian은 g와 u 진동자 상태의 회전 수준(정밀-파라 혼합이라고 함)을 혼합하여 정밀-파라 전환을^[9]^[10] 일으킬 수 있습니다.

핵

원자핵에서 각 핵자(양성자 또는 중성자)의 상태는 짝수 또는 홀수 패리티를 가지며, 핵자 구성은 핵껍질 모델을 사용하여 예측할 수 있다.원자 중의 전자는 홀수 패리티 상태의 핵자 수가 홀수일 경우에만 홀수 전체 패리티를 가진다.패리티는 일반적으로 핵 스핀 값 뒤에 +(짝수) 또는 -(홀수)로 표시됩니다.예를 들어 산소 동위원소는 O(5/2+)를 포함하며, 이는 스핀이 5/2이고 패리티가 짝수임을 의미합니다.셸 모델은 처음 16개의 핵자가 쌍으로 구성되어 각 쌍이 스핀 0과 짝수 패리티를 가지며, 마지막 핵자는 ^[11]d 오비탈에 대해 θ = 2 이후 짝수 패리티를 갖는 1d_5/2 쉘에 있기 때문이라고 설명한다.

양자장론

이 절의 내재적 패리티 할당은 양자장 이론뿐만 아니라 상대론적 양자역학에도 해당된다.

패리티( ${\hat {\mathcal {P}}}\left|0\right\rangle =\left|0\right\rangle$ ^ ${\hat {\mathcal {P}}}\left|0\right\rangle =\left|0\right\rangle$ 0 $math$ 0 ${\hat {\mathcal {P}}}\left|0\right\rangle =\left|0\right\rangle$ math 0 math \ $display$ $style$ $\ right$ \ $rangle$ = \ $left$ 0 \ $right$ \ $rangle$ )에서 진공 상태가 변하지 않음을 나타낼 수 있는 경우 해밀턴 값은 패리티 $\left[{\hat {H}},{\hat {\mathcal {P}}}\right]$ 불변 [ $\left[{\hat {H}},{\hat {\mathcal {P}}}\right]$ , P $\left[{\hat {H}},{\hat {\mathcal {P}}}\right]$ $]$ \ $displaystyle$ { $Hat$ { $\left[{\hat {H}},{\hat {\mathcal {P}}}\right]$ H $},$ 이온은 패리티 하에서는 변하지 않고, 그 결과 모든 상태가 양호한 패리티를 가지며, 이 패리티는 어떤 반응에서도 보존됩니다.

양자전기역학이 패리티 하에서는 불변함을 증명하기 위해서는 작용이 불변하고 양자화도 불변함을 증명해야 합니다.단순화를 위해 표준 양자화를 사용한다고 가정합니다. 그러면 구성에 의한 패리티 하에서는 진공 상태가 불변합니다.작용의 불변성은 맥스웰 방정식의 고전적 불변성에서 비롯된다.표준 양자화 절차의 불변성을 산출할 수 있으며, ^{[citation needed]}소멸 연산자의 변환에 따라 달라집니다.

Pa(p, ±)P⁺ = -aµp, ±)

여기서 p는 광자의 운동량을 나타내고 ±는 광자의 편광 상태를 나타냅니다.이것은 광자가 홀수 내적 패리티를 가지고 있다는 진술과 같다.마찬가지로 모든 벡터 보손은 홀수 내적 패리티를 가지며 모든 축 벡터는 짝수 내적 패리티를 갖습니다.

이러한 인수를 스칼라 필드 이론으로 쉽게 확장하면 스칼라에는 균등한 패리티가 있음을 알 수 있습니다.

Pa(p)P⁺ = a440p.

이것은 복잡한 스칼라 필드에서도 마찬가지입니다.(스피너의 자세한 내용은 디락 방정식에 관한 기사에서 다루어지고 있습니다.디락 방정식에서는 페르미온과 반피질은 정반대의 내적 패리티를 가지고 있는 것을 나타내고 있습니다.)

페르미온에는 스핀 그룹이 하나 이상 있기 때문에 약간의 합병증이 있습니다.

표준 모델의 패리티

글로벌 대칭 수정

패리티 연산자를 두 번 적용하면 좌표는 변경되지 않습니다. 즉, $P$ 는² 이론의 내부 대칭 중 하나로 작용해야 하며,^[12] 최대 상태 위상을 변경해야 합니다.예를 들어 표준 모델에는 바리온 번호 $B$ , 렙톤 $번호$ L 및 $전하$ Q와 같은 전하를 가진 세 개의 글로벌 U(1) 대칭이 있습니다.따라서 패리티 연산자는 $α$ , β 및 $δ$ 의 $일부$ 선택에 대해 $P iαB + iβL + iγQ$ = e를 $만족$ 합니다².또한 이 연산자는 새로운 패리티 연산자 P'에 $일부$ α에 대해 P $'$ = $P iαB$ e와 $같은$ 내부 대칭을 곱하여 항상 구성할 수 있다는 점에서 특이하지 않다.

패리티 연산자를 항상 P = $1$ 을 $만족$ 하도록² 정의할 수 있는지 확인하려면 이론에 존재하는 일부 내부 대칭 Q에 대해 P = $Q$ 인 $일반적$ 인² 경우를 고려하십시오.원하는 패리티 연산자는 $P'$ = $PQ$ 입니다^−1/2.Q가 연속 대칭 그룹의 일부라면 $Q$ 가^−1/2 존재하지만 이산 대칭의 일부라면 이 요소는 존재할 필요가 없으며 이러한 재정의는 ^[13]불가능할 수 있습니다.

표준 모델은 (- $1) F$ 대칭을 나타내며, $여기$ 서 F는 페르미온 수 연산자로 한 상태에 페르미온이 몇 개 있는지 계산합니다.표준 모델의 모든 입자는 F $= B$ + $L$ 을 $만족$ 하므로 이산 대칭도 e $연속 iα (B + L)$ 대칭 그룹의 일부입니다.만약 그 반전 연산자 P2)(−1)F에 만족했습니다. 그 때는 새로운 반전 연산자=1P2만족을 줄것을 하지만 다시 정의할 수 있다면 그 표준 모델은 지속적인 대칭 그룹의 F=1및 B+L=0, 이산 대칭(−1)F은 더 이상 일부이고 pari의 원하는 재정의가 마요라나의 뉴트 리노, 통합하여 확장된다.ty연산자를 수행할 수 없습니다.대신 P = $1$ 을 $만족$ 하므로⁴ 마요라나 중성미자는 ± $i$ 의내인성 패리티를 갖는다.

파이온의 패리티

1954년, 윌리엄 치노스키와 잭 스타인버거의 논문은 파이온이 ^[14]음의 동등성을 가지고 있다는 것을 증명했다.그들은 궤도 $~\mathbf {L} ={\boldsymbol {0}}~$ L $~\mathbf {L} ={\boldsymbol {0}}~$ $~\mathbf {L} ={\boldsymbol {0}}~$ (\ $displaystyle ~\mathbf {L}$ = bold $symbol {0}~})$ 인 $~\mathbf {L} ={\boldsymbol {0}}~$ 상태에서 중수소⁺
(²
₁H)와 음전하 파이온( $pion -$ )으로 이루어진 "원자"가 두 개의 중성자 $(\displaystyle$ n)로 붕괴되는 것을 연구했다.

중성자는 페르미온이기 때문에 페르미-디락 통계를 따르는데, 이는 최종 상태가 반대칭임을 의미한다.중수소가 1회전하고 파이온이 0회전한다는 사실을 이용하여 최종 상태의 반대칭성과 함께 두 중성자가 궤도 $~L=1~.$ L $~L=1~.$ 을 가져야 한다는 결론을 내렸다 $.$ {{ $displaystyle ~L=1~}$ 총 $~L=1~.$ 패리티는 입자의 고유 패리티와 구체의 외적 패리티의 곱이다. $~\left(-1\right)^{L}~.$ 고조파 함수 $~\left(-1\right)^{L}~.$ - 1) $~\left(-1\right)^{L}~.$ . {{ $displaystyle ~\left(-1\right)^{L}~.}$ 이 $~\left(-1\right)^{L}~.$ 과정에서 궤도운동량이 0에서 1로 변경되므로 총 패리티를 보존하기 위해서는 초입자와 최종입자의 고유 패리티 곱은 반대 부호가 있어야 한다.중수소 핵은 양성자와 중성자로 만들어지며, 따라서 양성자와 $~+1~$ 가 $~+1~$ + $1(\$ style ~+ $1~)$ 과 $~+1~$ 같은 내재적 패리티를 갖는다는 앞에서 언급한 규약을 사용하여 그들은 파이온의 패리티가 양성자와 중성자의 패리티를 나눈 두 중성자의 패리티의 곱에서 뺀 것과 같다고 주장했다.듀테론 ${\textstyle {\frac {(-1)(1)^{2}}{(1)^{2}}}=-1~,}$ 명시적으로 ${\textstyle {\frac {(-1)(1)^{2}}{(1)^{2}}}=-1~,}$ ( - ${\textstyle {\frac {(-1)(1)^{2}}{(1)^{2}}}=-1~,}$ ) ${\textstyle {\frac {(-1)(1)^{2}}{(1)^{2}}}=-1~,}$ ( 1) ${\textstyle {\frac {(-1)(1)^{2}}{(1)^{2}}}=-1~,}$ ( ${\textstyle {\frac {(-1)(1)^{2}}{(1)^{2}}}=-1~,}$ ) $=$ - 1 , {\ $textstyle$ {\ $frac {(-1)^{2}}{(1)^{2$ }}=- $1~,}.$ 여기서 ${\textstyle {\frac {(-1)(1)^{2}}{(1)^{2}}}=-1~,}$ 파이온이 의사칼라 입자라는 결론을 얻었다.

패리티 위반

P-대칭성:반사된 이미지처럼 만들어진 클럭은 원래 클럭의 반사된 이미지처럼 동작합니다.

P-비대칭성: 원래 클럭의 미러 이미지와는 달리 미러 이미지처럼 구축된 클럭입니다.

패리티는 전자기력과 중력에서는 보존되지만 약한 상호작용에서는 위반되며 강한 ^[15]^[16]상호작용에서는 어느 정도 위반될 수 있습니다.표준 모델에서는 약한 상호작용을 키랄 게이지 상호작용으로 표현하여 패리티 위반을 통합합니다.표준 모델에서 입자의 왼쪽 성분과 반입자의 오른쪽 성분만 하전된 약한 상호작용에 참여합니다.이는 패리티가 우리 우주의 대칭이 아님을 암시합니다. 숨겨진 거울 섹터가 존재하지 않는 한 패리티는 우리 우주의 대칭이 아닙니다.

1928년 R에 의해 행해진 알려지지 않은 실험입니다. T. Cox, G. C. McIlwraith, B.Kurrelmeyer는 사실상 약한 부패에서 패리티 위반을 보고했지만, 적절한 개념이 아직 개발되지 않았기 때문에 이러한 결과는 ^[17]영향을 미치지 않았다.1929년 헤르만 바일은 아무런 증거도 없이 스핀의 2성분 무질량 입자의 존재를 탐구했다.이 아이디어는 패리티 ^[18]위반을 암시했기 때문에 Pauli에 의해 거부되었습니다.

20세기 중반까지, 몇몇 과학자들에 의해 동등성이 보존되지 않을 수도 있다는 제안이 제기되었지만, 확실한 증거가 없다면 이러한 제안들은 중요하게 여겨지지 않았다.그 후 1956년 이론물리학자 리종다오(李 yang大^[19])와 양천닝( went天寧)의 신중한 검토와 분석은 더 나아가 패리티 보존이 강한 상호작용이나 전자기적 상호작용에 의해 소멸된 것으로 확인되었지만 약한 상호작용에서는 검증되지 않았다.그들은 몇 가지 가능한 직접 실험 테스트를 제안했다.그들은 대부분 ^{[citation needed]}무시당했지만, 리는 그의 콜롬비아 동료인 친슝 우를 설득해서 ^{[citation needed]}시도해 볼 수 있었다.그녀는 특별한 극저온 시설과 전문지식이 필요했고, 그래서 실험은 국립표준국에서 이루어졌다.

Wu, Ambler, Hayward, Hoppses 및 Hudson(1957)은 코발트-60의 ^[20]베타 붕괴에서 패리티 보존에 대한 명백한 위반을 발견했다.실험이 끝나자 우 씨는 이 씨와 양 씨에게 긍정적인 결과를 알려주고 추가 검사가 필요하다며 먼저 결과를 공개하지 말 것을 당부했다.그러나 이 씨는 1957년 1월 4일 컬럼비아 ^[21]물리학부의 금요일 점심 모임에서 이 같은 결과를 동료들에게 공개했다.이들 중 R.L. 가윈, L.M. 레더맨, R.M. 와인리치 등 3명은 기존 사이클로트론 실험을 수정해 패리티 ^[22]위반을 즉시 검증했다.이들은 우 씨의 연구팀이 준비될 때까지 연구 결과를 발표하지 않았고 두 논문은 같은 물리학 저널에 연달아 실렸다.

패리티 위반의 발견은 kaons의 물리학에서 뛰어난δ-δ 퍼즐을 즉시 설명했습니다.

2010년, 상대론적 중이온 충돌기와 함께 일하는 물리학자들이 쿼크-글루온 플라스마에서 단명 패리티 대칭을 깨는 기포를 만들어냈다고 보고되었다.STAR 협업을 통해 여러 물리학자가 수행한 실험에서 패리티는 강한 ^[16]상호작용에서도 위반될 수 있습니다.축전장의 변동에 의해 유발되는 효과와 유사한 국소 패리티 위반은 키랄 자기 ^[23]^[24]효과에 의해 나타날 것으로 예측된다.

강입자의 고유 패리티

자연이 패리티를 유지하는 한 모든 입자에 고유한 패리티를 할당할 수 있습니다.약한 상호작용은 그렇지 않지만 강입자를 생성하는 강한 상호작용 반응을 조사하거나 파이온에 대한 로 중간자 붕괴와 같은 약한 상호작용을 포함하지 않는 붕괴를 통해 강입자에 패리티를 할당할 수 있다.

「」를 참조해 주세요.

레퍼런스

각주

^ 질량 유량의 예는 강이 침전물을 이동하는 방향과 속도(중량 기준)이다.이것은 선형 운동량의 복합 형태이며 매체를 통한 소리 진동 흐름과 밀접하게 관련되어 있습니다.

인용문

^ Levine, Ira N. (1991). Quantum Chemistry (4th ed.). Prentice-Hall. p. 163. ISBN 0-205-12770-3.
^ Levine, Ira N. (1991). Quantum Chemistry (4th ed.). Prentice-Hall. p. 355. ISBN 0-205-12770-3.
^ ^a ^b Andrew, A. V. (2006). "2. Schrödinger equation". Atomic spectroscopy. Introduction of theory to Hyperfine Structure. p. 274. ISBN 978-0-387-25573-6.
^ Mladen Georgiev (20 November 2008). "Parity non-conservation in β-decay of nuclei: revisiting experiment and theory fifty years after. IV. Parity breaking models". p. 26. arXiv:0811.3403 [physics.hist-ph].
^ Bransden, B. H.; Joachain, C. J. (2003). Physics of Atoms and Molecules (2nd ed.). Prentice Hall. p. 204. ISBN 978-0-582-35692-4.
^ NIST 원자 스펙트럼 데이터베이스 질소 원자 에너지 수준을 읽으려면 Spectrum 상자에 "N I"를 입력하고 Retrieve data를 클릭합니다.
^ Longuet-Higgins, H.C. (1963). "The symmetry groups of non-rigid molecules". Molecular Physics. 6 (5): 445–460. Bibcode:1963MolPh...6..445L. doi:10.1080/00268976300100501.
^ P.R. 벙커와 P.Jensen(2005), 분자대칭의 기초(CRC Press) ISBN 0-7503-0941-5 [1]
^ Pique, J. P.; et al. (1984). "Hyperfine-Induced Ungerade-Gerade Symmetry Breaking in a Homonuclear Diatomic Molecule near a Dissociation Limit: $^{127}$ I $_{2}$ at the $^{2}P_{3/2}$ − $^{2}P_{1/2}$ Limit". Phys. Rev. Lett. 52 (4): 267–269. Bibcode:1984PhRvL..52..267P. doi:10.1103/PhysRevLett.52.267.
^ Critchley, A. D. J.; et al. (2001). "Direct Measurement of a Pure Rotation Transition in H $_{2}^{+}$ ". Phys. Rev. Lett. 86 (9): 1725–1728. Bibcode:2001PhRvL..86.1725C. doi:10.1103/PhysRevLett.86.1725. PMID 11290233.
^ Cottingham, W.N.; Greenwood, D.A. (1986). An introduction to nuclear physics. Cambridge University Press. p. 57. ISBN 0-521-31960-9.
^ Weinberg, Steven (1995). "16". The Quantum Theory of Fields Volume 1. Vol. 4. Cambridge University Press. p. 124-126. ISBN 9780521670531.
^ Feinberg, G.; Weinberg, S. (1959). "On the phase factors in inversions". Il Nuovo Cimento. 14 (3): 571–592. doi:10.1007/BF02726388.
^ Chinowsky, W.; Steinberger, J. (1954). "Absorption of Negative Pions in Deuterium: Parity of the Pion". Physical Review. 95 (6): 1561–1564. Bibcode:1954PhRv...95.1561C. doi:10.1103/PhysRev.95.1561.
^ Gardner, Martin (1969) [1964]. The Ambidextrous Universe; Left, Right, and the Fall of Parity (rev. ed.). New York: New American Library. p. 213.
^ ^a ^b Muzzin, S.T. (19 March 2010). "For one tiny instant, physicists may have broken a law of nature". PhysOrg. Retrieved 5 August 2011.
^ Roy, A. (2005). "Discovery of parity violation". Resonance. 10 (12): 164–175. doi:10.1007/BF02835140. S2CID 124880732.
^ Wu, Chien-Shiung (2008), "The Discovery of the Parity Violation in Weak Interactions and Its Recent Developments", Nishina Memorial Lectures, Lecture Notes in Physics, Tokyo: Springer Japan, vol. 746, pp. 43–70, doi:10.1007/978-4-431-77056-5_4, ISBN 978-4-431-77055-8, retrieved 29 August 2021
^ Lee, T.D.; Yang, C.N. (1956). "Question of Parity Conservation in Weak Interactions". Physical Review. 104 (1): 254–258. Bibcode:1956PhRv..104..254L. doi:10.1103/PhysRev.104.254.
^ Wu, C.S.; Ambler, E; Hayward, R.W.; Hoppes, D.D.; Hudson, R.P. (1957). "Experimental test of parity conservation in beta decay". Physical Review. 105 (4): 1413–1415. Bibcode:1957PhRv..105.1413W. doi:10.1103/PhysRev.105.1413.
^ Caijian, Jiang (1 August 1996). Wu jian xiong-wu li ke xue de si yi fu ren 吳健雄: 物理科學的第一夫人 [Wu Jianxiong: The first lady of physical sciences] (in Chinese). 江才健 (author/biographer). 時報文化出版企業股份有限公司 (Times Culture Publishing Enterprise). p. 216. ISBN 978-957132110-3.{{cite book}}: CS1 maint: 무시된 ISBN 오류(링크) ISBN 957-13-2110-9
^ Garwin, R.L.; Lederman, L.M.; Weinrich, R.M. (1957). "Observations of the failure of conservation of parity and charge conjugation in meson decays: The magnetic moment of the free muon". Physical Review. 105 (4): 1415–1417. Bibcode:1957PhRv..105.1415G. doi:10.1103/PhysRev.105.1415.
^ Kharzeev, D.E.; Liao, J. (2 January 2019). "Isobar collisions at RHIC to test local parity violation in strong interactions". Nuclear Physics News. 29 (1): 26–31. doi:10.1080/10619127.2018.1495479. ISSN 1061-9127. S2CID 133308325.
^ Zhao, Jie; Wang, Fuqiang (July 2019). "Experimental searches for the chiral magnetic effect in heavy-ion collisions". Progress in Particle and Nuclear Physics. 107: 200–236. arXiv:1906.11413. Bibcode:2019PrPNP.107..200Z. doi:10.1016/j.ppnp.2019.05.001. S2CID 181517015.

원천

Perkins, Donald H. (2000). Introduction to High Energy Physics. ISBN 9780521621960.
Sozzi, M. S. (2008). Discrete symmetries and CP violation. Oxford University Press. ISBN 978-0-19-929666-8.
Bigi, I. I.; Sanda, A. I. (2000). CP Violation. Cambridge Monographs on Particle Physics, Nuclear Physics and Cosmology. Cambridge University Press. ISBN 0-521-44349-0.
Weinberg, S. (1995). The Quantum Theory of Fields. Cambridge University Press. ISBN 0-521-67053-5.

[1] 질량 유량의 예는 강이 침전물을 이동하는 방향과 속도(중량 기준)이다.이것은 선형 운동량의 복합 형태이며 매체를 통한 소리 진동 흐름과 밀접하게 관련되어 있습니다.

[2] Levine, Ira N. (1991). Quantum Chemistry (4th ed.). Prentice-Hall. p. 163. ISBN 0-205-12770-3.

[3] Levine, Ira N. (1991). Quantum Chemistry (4th ed.). Prentice-Hall. p. 355. ISBN 0-205-12770-3.

[Andrew,_chapter_2-4] Andrew, A. V. (2006). "2. Schrödinger equation". Atomic spectroscopy. Introduction of theory to Hyperfine Structure. p. 274. ISBN 978-0-387-25573-6.

[5] Mladen Georgiev (20 November 2008). "Parity non-conservation in β-decay of nuclei: revisiting experiment and theory fifty years after. IV. Parity breaking models". p. 26. arXiv:0811.3403 [physics.hist-ph].

[6] Bransden, B. H.; Joachain, C. J. (2003). Physics of Atoms and Molecules (2nd ed.). Prentice Hall. p. 204. ISBN 978-0-582-35692-4.

[NIST-7] NIST 원자 스펙트럼 데이터베이스 질소 원자 에너지 수준을 읽으려면 Spectrum 상자에 "N I"를 입력하고 Retrieve data를 클릭합니다.

[Longuet-Higgins1963-8] Longuet-Higgins, H.C. (1963). "The symmetry groups of non-rigid molecules". Molecular Physics. 6 (5): 445–460. Bibcode:1963MolPh...6..445L. doi:10.1080/00268976300100501.

[9] P.R. 벙커와 P.Jensen(2005), 분자대칭의 기초(CRC Press) ISBN 0-7503-0941-5 [1]

[10] Pique, J. P.; et al. (1984). "Hyperfine-Induced Ungerade-Gerade Symmetry Breaking in a Homonuclear Diatomic Molecule near a Dissociation Limit: $^{127}$ I $_{2}$ at the $^{2}P_{3/2}$ − $^{2}P_{1/2}$ Limit". Phys. Rev. Lett. 52 (4): 267–269. Bibcode:1984PhRvL..52..267P. doi:10.1103/PhysRevLett.52.267.

[Critchley2001-11] Critchley, A. D. J.; et al. (2001). "Direct Measurement of a Pure Rotation Transition in H $_{2}^{+}$ ". Phys. Rev. Lett. 86 (9): 1725–1728. Bibcode:2001PhRvL..86.1725C. doi:10.1103/PhysRevLett.86.1725. PMID 11290233.

[12] Cottingham, W.N.; Greenwood, D.A. (1986). An introduction to nuclear physics. Cambridge University Press. p. 57. ISBN 0-521-31960-9.

[13] Weinberg, Steven (1995). "16". The Quantum Theory of Fields Volume 1. Vol. 4. Cambridge University Press. p. 124-126. ISBN 9780521670531.

[14] Feinberg, G.; Weinberg, S. (1959). "On the phase factors in inversions". Il Nuovo Cimento. 14 (3): 571–592. doi:10.1007/BF02726388.

[15] Chinowsky, W.; Steinberger, J. (1954). "Absorption of Negative Pions in Deuterium: Parity of the Pion". Physical Review. 95 (6): 1561–1564. Bibcode:1954PhRv...95.1561C. doi:10.1103/PhysRev.95.1561.

[16] Gardner, Martin (1969) [1964]. The Ambidextrous Universe; Left, Right, and the Fall of Parity (rev. ed.). New York: New American Library. p. 213.

[:0-17] Muzzin, S.T. (19 March 2010). "For one tiny instant, physicists may have broken a law of nature". PhysOrg. Retrieved 5 August 2011.

[18] Roy, A. (2005). "Discovery of parity violation". Resonance. 10 (12): 164–175. doi:10.1007/BF02835140. S2CID 124880732.

[19] Wu, Chien-Shiung (2008), "The Discovery of the Parity Violation in Weak Interactions and Its Recent Developments", Nishina Memorial Lectures, Lecture Notes in Physics, Tokyo: Springer Japan, vol. 746, pp. 43–70, doi:10.1007/978-4-431-77056-5_4, ISBN 978-4-431-77055-8, retrieved 29 August 2021

[20] Lee, T.D.; Yang, C.N. (1956). "Question of Parity Conservation in Weak Interactions". Physical Review. 104 (1): 254–258. Bibcode:1956PhRv..104..254L. doi:10.1103/PhysRev.104.254.

[Wu-Ambler-Hayward-etal-1957-21] Wu, C.S.; Ambler, E; Hayward, R.W.; Hoppes, D.D.; Hudson, R.P. (1957). "Experimental test of parity conservation in beta decay". Physical Review. 105 (4): 1413–1415. Bibcode:1957PhRv..105.1413W. doi:10.1103/PhysRev.105.1413.

[22] Caijian, Jiang (1 August 1996). Wu jian xiong-wu li ke xue de si yi fu ren 吳健雄: 物理科學的第一夫人 [Wu Jianxiong: The first lady of physical sciences] (in Chinese). 江才健 (author/biographer). 時報文化出版企業股份有限公司 (Times Culture Publishing Enterprise). p. 216. ISBN 978-957132110-3.{{cite book}}: CS1 maint: 무시된 ISBN 오류(링크) ISBN 957-13-2110-9

[23] Garwin, R.L.; Lederman, L.M.; Weinrich, R.M. (1957). "Observations of the failure of conservation of parity and charge conjugation in meson decays: The magnetic moment of the free muon". Physical Review. 105 (4): 1415–1417. Bibcode:1957PhRv..105.1415G. doi:10.1103/PhysRev.105.1415.

[24] Kharzeev, D.E.; Liao, J. (2 January 2019). "Isobar collisions at RHIC to test local parity violation in strong interactions". Nuclear Physics News. 29 (1): 26–31. doi:10.1080/10619127.2018.1495479. ISSN 1061-9127. S2CID 133308325.

[25] Zhao, Jie; Wang, Fuqiang (July 2019). "Experimental searches for the chiral magnetic effect in heavy-ion collisions". Progress in Particle and Nuclear Physics. 107: 200–236. arXiv:1906.11413. Bibcode:2019PrPNP.107..200Z. doi:10.1016/j.ppnp.2019.05.001. S2CID 181517015.

[a]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

v t C, P 및 T의 대칭
C대칭성 P대칭성 T대칭성
CP CP 대칭 CPT 대칭
키라리티 핀군

Search

패리티(물리학)

네임스페이스

더

목차