히우드 그래프

Heawood graph
히우드 그래프
Heawood Graph.svg
이름을 따서 명명됨퍼시 존 히우드
정점14
가장자리21
반지름3
지름3
둘레6
자동형성336(PGL2(7))
색수2
색도 지수3
속1
책두께3
대기열 번호2
특성.양립자
큐빅
케이지
거리-변환
거리-정규어
토로이드
해밀턴어
대칭
오리엔테이블 심플
그래프 및 모수 표

그래프 이론의 수학적 분야에서 히우드 그래프는 14개의 정점과 21개의 가장자리를 가진 비방향 그래프로, 퍼시 존 히우드의 이름을 따서 이름 지어졌다.[1]

조합 특성

그래프는 세제곱이고, 그래프의 모든 사이클은 6개 이상의 가장자리를 가진다.모든 작은 입방형 그래프는 주기가 짧기 때문에 이 그래프는 6번째 입방형 그래프 중에서 가장 작은 입방형 그래프인 6-cage이다.거리 변환 그래프( 포스터 인구 조사 참조)[2]이므로 거리 정규 그래프.

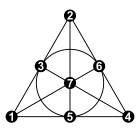
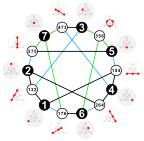
Heawood 그래프에는 24개의 완벽한 일치가 있다. 각 일치는 일치가 아닌 가장자리 집합이 해밀턴 사이클을 형성한다.예를 들어, 그림에는 사이클에 배치된 그래프의 정점이 표시되며 사이클의 내부 대각선이 일치를 형성한다.사이클 가장자리를 두 개의 일치로 세분화함으로써, 우리는 8가지 다른 방법으로 희우드 그래프를 세 개의 완벽한 일치(가장자리 3색)로 분할할 수 있다.[2]두 번의 완벽한 매칭, 그리고 두 번의 해밀턴 사이클은 그래프의 대칭에 의해 서로 변형될 수 있다.[3]

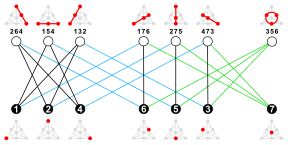
히우드 그래프에는 28개의 6Vertex 사이클이 있다.각 6 사이클은 정확히 세 개의 다른 6 사이클에서 분리된다. 이 3개의 6 사이클 중 각 사이클은 다른 2개의 대칭적 차이점이다.6 사이클당 하나의 노드와 각 6 사이클 쌍에 하나의 에지가 있는 그래프는 Coxeter 그래프다.[4]

기하학적 및 위상학적 특성

히우드 그래프는 토로이드 그래프인데, 즉 토러스 위에 교차하지 않고 삽입할 수 있다.이러한 유형의 한 가지 내장에서는 정점과 가장자리를 3차원 유클리드 공간에 토폴로지인 질라시 다면체의 토폴로지를 가진 비콘벡스 다면체의 정점과 가장자리 집합으로 배치한다.

이 그래프는 1890년에 토러스 부분을 폴리곤으로 분할할 때마다 폴리곤 영역은 최대 7가지 색으로 채색될 수 있다는 것을 증명했던 퍼시 존 히우드의 이름을 따서 명명되었다.[5][6]히우드 그래프는 서로 인접한 7개 영역으로 토러스 구획을 형성하여 이 한계가 팽팽함을 보여준다.

Pano 평면 및 Levi 그래프의 두 가지 표현(아래는 초당적 그래프)

Heawood 그래프는 Fano 평면의 Levi 그래프로, 그 기하학에서 점과 선 사이의 근친상간을 나타낸다.이러한 해석으로 헤이워드 그래프에서 6주기는 파노 평면의 삼각형에 해당한다.또한, Heawood 그래프는 그룹3 SL(F2)의 Tits 빌딩이다.

히우드 그래프는 교차 번호 3을 가지며 교차 번호(OEIS에서 연속 A110507)를 가진 가장 작은 입방 그래프다.히우드 그래프를 포함하여, 8개의 순서 14의 교차 번호 3의 구별되는 그래프가 있다.

히우드 그래프는 콜린 드 베르디에르 그래프 불변 μ = 6으로 가장 작은 입방 그래프다.

Heawood 그래프는 단위 거리 그래프로서, 인접한 정점이 정확히 1 떨어져 있는 거리에 있도록 평면에 삽입할 수 있으며, 두 정점이 동일한 지점에 내장되어 있지 않으며, 가장자리 내의 한 점에 정점이 내장되어 있지 않다.[8]

대수적 특성

Heawood 그래프의 자동형 집단은 336 순서의 집단인 투영 선형 집단 PGL2(7)에 이형이다.[9]그것은 정점, 가장자리, 그리고 그래프의 호에서 전이적으로 작용한다.따라서 희우드 그래프는 대칭 그래프다.그것은 어떤 정점과 어떤 가장자리로도 가져가는 자동모형을 가지고 있다.더 강하게 말하면, 히우드 그래프는 4아크 변환이다.[10]포스터 인구조사에 따르면 F014A로 참조되는 히우드 그래프는 14개의 정점에 대한 유일한 입방 대칭 그래프다.[11][12]

책 두께 3과 줄 2가 있다.[13]

Heawood 그래프의 특성 다항식은(- )(+ ) - 2) }-2이며 이 특성 다항식을 가진 유일한 그래프로서 스펙트럼에 의해 결정되는 그래프가 된다.

갤러리

참조

  1. ^ Weisstein, Eric W. "Heawood Graph". MathWorld.
  2. ^ a b Brouwer, Andries E. "Heawood graph". Distance-Lography Graph에 대한 추가 및 수정(Brower, Cohen, Neumaer; Springer; 1989년)
  3. ^ Abreu, M.; Aldred, R. E. L.; Funk, M.; Jackson, Bill; Labbate, D.; Sheehan, J. (2004), "Graphs and digraphs with all 2-factors isomorphic", Journal of Combinatorial Theory, Series B, 92 (2): 395–404, doi:10.1016/j.jctb.2004.09.004, MR 2099150.
  4. ^ Dejter, Italo J. (2011), "From the Coxeter graph to the Klein graph", Journal of Graph Theory, 70: 1–9, arXiv:1002.1960, doi:10.1002/jgt.20597, S2CID 754481.
  5. ^ Brown, Ezra (2002). "The many names of (7,3,1)" (PDF). Mathematics Magazine. 75 (2): 83–94. doi:10.2307/3219140. JSTOR 3219140. Archived from the original (PDF) on 2012-02-05. Retrieved 2006-10-27.
  6. ^ Heawood, P. J. (1890). "Map colouring theorems". Quarterly Journal of Mathematics. First Series. 24: 322–339.
  7. ^ Hein van der Holst (2006). "Graphs and obstructions in four dimensions" (PDF). Journal of Combinatorial Theory, Series B. 96 (3): 388–404. doi:10.1016/j.jctb.2005.09.004.
  8. ^ Gerbracht, Eberhard H.-A. (2009). "Eleven unit distance embeddings of the Heawood graph". arXiv:0912.5395. Bibcode:2009arXiv0912.5395G. {{cite journal}}: 인용문은 (도움이) 필요하다.
  9. ^ Bondy, J. A.; Murty, U. S. R. (1976). Graph Theory with Applications. New York: North Holland. p. 237. ISBN 0-444-19451-7. Archived from the original on 2010-04-13. Retrieved 2019-12-18.
  10. ^ Conder, Marston; Morton, Margaret (1995). "Classification of Trivalent Symmetric Graphs of Small Order" (PDF). Australasian Journal of Combinatorics. 11: 146.
  11. ^ 로일, G. "큐빅 대칭 그래프 (The Foster Sensitures)"웨이백 머신에 보관된 2008-07-20
  12. ^ 콘더, M., 도브사니, P. "삼각형 대칭 그래프 최대 768정점까지." J. 콤빈수학. 콤빈.계산하다.40, 41-63, 2002.
  13. ^ 제시카 울즈, SAT와 함께 선형 배치 엔지니어링.2018년 튀빙겐 대학교 석사 논문