최단 경로 트리
Shortest-path tree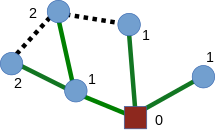
수학과 컴퓨터 과학에서, 연결된 무방향 그래프 G의 정점 v에 근을 둔 최단 경로 트리는 G의 신장 트리 T이며, 따라서 루트 v에서 다른 정점 u까지의 경로 거리는 G의 v에서 u까지의 최단 경로 거리입니다.
최단 경로가 잘 정의된 연결된 그래프(즉, 음의 길이 사이클이 없는 경우)에서는 다음 알고리즘을 사용하여 최단 경로 트리를 구성할 수 있습니다.
- 계산 dist(u)는 Dijkstra의 알고리즘 또는 Bellman-Ford 알고리즘을 사용하여 G에서 루트 v에서 정점 u까지의 최단 경로 거리입니다.
- 루트가 아닌 모든 정점 u에 대해 p가 u에 연결되고 dist(p) + edge_dist(p,u) = dist(u)가 되도록 상위 정점 p를 u에 할당할 수 있습니다.p에u 대한 선택사항이 여러 개 존재할 경우에는 가능한 한 적은 수의 간선으로 v에서 p로의u 최단 경로가 존재할 p를u 선택합니다. 이 타이브레이킹 규칙은 0-길이 사이클이 존재할 때 루프를 방지하기 위해 필요합니다.
- 각 노드와 부모 노드 사이의 가장자리를 사용하여 최단 경로 트리를 구성합니다.
위 알고리즘은 최단 경로 트리의 존재를 보장합니다.최소 신장 트리와 마찬가지로, 일반적으로 최단 경로 트리는 고유하지 않습니다.
모든 에지 가중치가 동일한 그래프에서 최단 경로 트리는 너비 우선 검색 트리와 일치합니다.
음의 주기를 갖는 그래프에서는 v에서 다른 모든 정점으로 가는 가장 짧은 단순 경로 집합이 반드시 트리를 형성하지는 않습니다.
단순하게 연결된 그래프의 경우, 최단 경로 트리를 사용하여[1] 두 네트워크 중심성 측도 간의 비선형 관계, 근접성 및 정도를 제시할 수 있습니다.가장 짧은 경로 트리의 가지가 하나의 네트워크의 어떤 루트 노드에 대해서도 통계적으로 유사하다고 가정하면, 가지의 크기는 루트 정점에 연결된 가지의 수, 즉 루트 노드의 정도에만 의존한다는 것을 보여줄 수 있습니다.이를 통해 각 정점과 관련된 길이 척도인 근접도의 역수가 정도의 로그에 따라 거의 선형적으로 변한다는 것을 추론할 수 있습니다.이 관계는 정확하지 않지만 실제 데이터로[1] 구성된 많은 네트워크에서 근접도와 정도 사이의 상관 관계를 포착하며 이러한 성공은 최단 경로 트리가 네트워크 분석에서 유용한 근사치가 될 수 있음을 시사합니다.
참고 항목
참고문헌
- ^ a b Evans, Tim S.; Chen, Bingsheng (2022). "Linking the network centrality measures closeness and degree". Communications Physics. 5 (1): 172. doi:10.1038/s42005-022-00949-5. hdl:10044/1/97904. ISSN 2399-3650.
참고문헌
Cahn, Robert S. (1998). Wide Area Network Design: Concepts and Tools for Optimization. Networking. Morgan Kaufmann. ISBN 978-1558604582.


