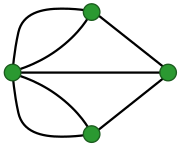
핸드셰이킹

수학의 한 분야인 그래프 이론에서, 악수하는 보조정리법은 모든 유한한 비방향 그래프에서, 홀수 수의 가장자리를 건드리는 정점의 수가 짝수라는 것이다.더 구어적으로 말하면, 몇몇이 악수를 하는 파티에서, 홀수 다른 사람의 손을 흔드는 사람들의 수는 짝수다.^[1]핸드셰이킹 보조정리(handshake lema)는 도합 공식의 결과로서, 때로는 핸드셰이킹 보조정리라고도 불리는데,^[2] 이에 따라 도합(각 꼭지점이 닿은 횟수)은 그래프에 있는 가장자리 수의 두 배와 같다.두 결과 모두 레온하르트 오일러(1736년)가 그래프 이론 연구를 시작한 쾨니히스베르크의 일곱 다리(Seven Bridges of Königsberg)에 관한 그의 유명한 논문에서 입증되었다.^[3]

쾨니히스베르크의 다리 너머와 그들의 일반화와 오일러 투어에 이르기까지, 다른 애플리케이션은 특정 결합 구조물의 경우 구조물의 수가 항상 균등하다는 것을 증명하고, 슈페너의 보조정리 및 등산 문제에 대한 증거를 지원하는 것을 포함한다.복잡도 등급 PPA는 큰 암묵적으로 정의된 그래프에서 그러한 꼭지점이 주어진 경우 두 번째 홀수 정점을 찾는 어려움을 캡슐화한다.

정의 및 문

비방향 그래프는 정점의 시스템과 순서가 정점의 쌍을 연결하는 가장자리로 구성된다.모든 그래프에서 꼭지점 $v{\displaystyle }$ ${\displaystyle v}$의 ${\displaystyle 도}$ ${\displaystyle (v}$) ${\displaystyle \deg(v)}$은 $v{\displaystyle }$ ${\displaystyle$ v$}$을(를) 끝점으로 하는 가장자리$$ 수로 정의된다$$.꼭지점을 자신에게 연결하는 루프를 포함할 수 있는 그래프의 경우, 루프는 핸드셰이킹 보조정리 목적으로 엔드포인트의 정도에 기여하는 두 개의 단위로 계산되어야 한다.^[2]그 다음, 핸드셰이킹 보조정리기는 모든 유한 그래프에서, ${\displaystyle \mathrm{deg})}$(${\displaystyle v}$ $){\displaystyle \deg(v)}$가 홀수인$$ 정점의 짝수가 있어야 한다고 명시한다.^[1]그래프에서 홀수도의 정점을 홀수 노드^[4] 또는 홀수 정점이라고 부르기도 한다.^[5] 이 용어에서 핸드셰이킹 보조정리기는 모든 그래프에 짝수 수의 홀수 노드가 있다는 문장으로 바꾸어 말할 수 있다.^[4][5]

도합 공식에는 다음과 같이 명시되어 있다.

여기서 $V{\displaystyle }$ ${\displaystyle V}$은(는) 그래프에서 정점 집합이고 $E{\displaystyle }$ ${\displaystyle E}$은(는) 그래프에서 가장자리 집합이다.즉, 정점도의 합은 가장자리 수의 두 배와 같다.^[6]지시된 그래프에서 도합 공식의 또 다른 형태는 모든 정점의 도합과 도수의 합이 둘 다 에지 수와 같다고 말한다.여기서 인도는 들어오는 가장자리의 수, 아웃도는 나가는 가장자리의 수입니다.^[7]학위합계 공식의 버전은 유한한 집합 집합 집합 또는 동등하게 다중 문자에도 적용된다. 원소의 도합(도가 이를 포함하는 집합의 수와 동일함)은 항상 집합의 추기경합과 같다.^[8]

두 결과 모두 주어진 그래프의 하위 그래프에도 적용되며, 특히 연결된 구성요소에 적용된다.그 결과, 어떤 홀수 정점에 대해서도 다른 홀수 정점에 연결하는 경로가 존재해야 한다.^[9]

적용들

오일러 경로 및 투어

레온하르트 오일러는 쾨니히스베르크 7교(현 칼리닌그라드)가 일곱 다리를 각각 한 번씩 건너는 쾨니히스베르크(현 칼리닌그라드)시의 도보여행을 요청하면서 쾨니히스베르크 7교에서 손짓 보조마사를 처음 입증했다.이것은 도시와 그 다리를 나타내는 연결된 그래프의 오일러 경로나 오일러 투어를 요청하는 것으로 그래프 이론적 용어로 번역할 수 있다: 오일러 경로의 경우 시작점과는 다른 정점에서 끝나거나 오일러에서 시작점으로 되돌아가는 각 가장자리를 한 번 가로지르는 그래프를 통과하는 것이다.ur. 오일러는 이 문제에 대한 근본적인 결과를 그래프의 홀수 정점의 수로 나타냈는데, 이는 핸드셰이킹 보조정리기가 짝수로 제한한다.이 숫자가 0이면 오일러 투어가, 2이면 오일러 경로가 존재한다.그렇지 않으면 문제를 해결할 수 없다.쾨니히스베르크 7대교의 경우 문제를 나타내는 그래프는 정점이 4개 이상이며, 오일러 경로나 오일러 투어도 없다.^[3]

크리스토피데스-에Serdyukov 알고리즘은 여행 영업사원 문제에 근사치를 하는데, 홀수 정점의 수가 핵심 역할을 하기 때문에, 오일러 투어가 근사 TSP 투어를 형성하는 그래프를 구성하기 위해 알고리즘이 이러한 정점을 쌍으로 연결할 수 있다.^[10]

콤비네이터 열거

여러 조합 구조물은 적절한 "교환 그래프"^[11]의 홀수 정점과 연관시켜 짝수인 것으로 보일 수 있다.

예를 들어, C로서. A. B. Smith는 어떤 입방 $그래프{\displaystyle }$ G ${\displaystyle G}$에서 어떤 고정 에지 ${\displaystyle u}$ v ${\displaystyle uv}$을 통해서도 해밀턴 사이클 수가 짝수여야 함을 증명했다$;$ 이것들은 각 꼭지점을 정확히 한 번 통과하는 사이클이다.Thomason(1978)은 이 결과를 모든 정점이 홀수 정도를 갖는 그래프까지 확대하기 위해 핸드셰이킹 보조마사에 기초한 증거를 사용했다.Thomason은 교환 그래프 $H{\displaystyle }$ ${\displaystyle H}$을 정의하는데$,$ 그 정점은 $u{\displaystyle }$ ${\displaystyle u}$에서 시작하여$$$$ 엣지 ${\displaystyle u}$ v ${\displaystyle uv}$까지 이어지는 $G{\displaystyle }$ ${\displaystyle G}$의 해밀턴 경로와 일대일 일치한다$.$$p{\displaystyle {}_{}}$ 1 ${\displaystyle {p\mathrm{}}_{}}$${\$ $p_{1}}$와 ${\displaystyle {p\mathrm{}}_{}}$ 2$${\$displaystyle$ $p_{2}}:$ p ${\displaystyle 1_{}}$의 끝에 새 엣지를 $추가$하고 p의 중간에서 다른 엣지를$$ ${\displaystyle {제거}_{}}$하여 p$$2 {\$displaystyp p_{$$1$}를 얻을 수 있는 경우$$ $H{\displaystyle }${\$displaystystystyle H}$의 엣지에 의해 연결된 것으로$$ 정의된다.${\displaystyle 1_{}}$ ${\$이 작업은 대칭 관계를 형성하여 되돌릴 수 있으므로 $H{\displaystyle }$ ${\displaystyle H}$은(는) 비방향 그래프다$$.경로 $p{\displaystyle }$ ${\displaystyle p}$이$($가) $정점{\displaystyle }$ w ${\displaystyle w}$에서 끝나는$$ 경우 $H{\displaystyle }$ ${\displaystyle$ $H$$}$에서 $p$ ${\displaystyle$ p$}$에 해당하는 정점은 p ${\displaystyle p}$이(가) 다시$u{\displaystyle }$ {\$displaysty u}$에 연결되지 않는 에지로 확장될$$ 수 있는 방법의 수와 같다$$$.$of this vertex in ${\displaystyle H}$ is either ${\displaystyle \deg(w)-1}$ (an even number) if ${\displaystyle p}$ does not form part of a Hamiltonian cycle through ${\displaystyle uv}$, or ${\displaystyle \deg(w)-2}$ (an odd number) if ${\displaystyle p}$ is part of a해밀턴 사이클은 ${\displaystyle u}$ v ${\displaystyle uv}$을 $통과$한다$.$ H {\$displaystyle$ H$}$은(는) 짝수 수의 홀수 정점을 가지므로$$ $G{\displaystyle }$ ${\displaystyle$ G$}$은(는) ${\displaystyle u}$ v ${\displaysty uv}$을 통해 짝수 수의 해밀턴 사이클을 가져야 한다$$$.$^[12]

기타 응용 프로그램

악수하는 보조정리법과 학위합계식도 수학에서 몇 가지 다른 결과를 증명하는 데 사용된다.여기에는 다음이 포함된다.

• 스퍼너의 보조정리에서는 큰 삼각형을 가장자리 대 가장자리와 만나는 작은 삼각형으로 세분하고 정점에는 세 가지 색상으로 라벨을 붙여 큰 삼각형의 각 가장자리를 따라 두 가지 색상만 사용한다면, 작은 삼각형 중 적어도 하나의 삼각형이 세 가지 색상의 정점을 가지며, 고정점 이론으로 응용할 수 있다., 뿌리 찾기 알고리즘, 그리고 공정한 분배.이 보조마사의 한 증거는 교환 그래프를 형성하는데, 그 끝점이 삼각형(작고 크며)이고 가장자리가 특정 두 색상의 두 정점을 공유하는 삼각형 쌍을 연결한다.큰 삼각형은 이 교환 그래프에서 반드시 홀수도를 가지고 있는데, 세 가지 색상을 모두 가진 작은 삼각형이 그러하듯이 다른 작은 삼각형은 그렇지 않다.손흔들리는 보조정리기로 세 가지 색상을 모두 가진 작은 삼각형의 홀수가 있어야 하고, 따라서 적어도 그런 삼각형이 하나 이상 존재해야 한다.^[13]

• 등산문제는 단위간격에서 충분히 품행이 단정하고, 단위간격의 끝에 동일한 값을 갖는 기능을 위해, 간격의 반대쪽 끝에서 시작하여 두 지점의 움직임을 조정하여, 모에 걸쳐 동일한 값의 지점에 머무르면서 중간 어딘가에서 만날 수 있도록 하는 것이 가능하다고 기술하고 있다.이에 대한 하나의 증거는 동일한 극한점을 가진 조각으로 된 선형 함수에 의한 함수 근사치, 단위 사각형의 단일 점의 좌표로 두 이동 점의 위치를 매개변수로 나타내며, 두 점의 가용 위치가 이 사각형에 내장된 유한 그래프를 형성한다는 것을 보여준다.출발 위치와 그 반전이 홀수 정점이다.악수하는 보조정리기로 이 두 위치는 그래프의 연결된 동일한 구성요소에 속하며, 한 위치에서 다른 위치로 가는 경로는 반드시 원하는 만남 지점을 통과한다.^[14]
• 재건 추측은 그래프에서 하나의 꼭지점을 제거하여 형성된 여러 개의 서브그래프에서 그래프의 구조를 고유하게 결정하는 문제를 다루고 있다.이 정보를 고려할 때, 도-섬 공식을 사용하여 주어진 그래프에서 가장자리 수와 각 꼭지점의 정도를 복구할 수 있다.이를 통해 주어진 그래프가 정규 그래프인지 여부를 판단할 수 있으며, 그렇게 되면 너무 낮은 수준의 모든 서브그래프 정점에 대해 새로운 이웃을 추가하여 정점 삭제된 서브그래프에서 고유하게 결정할 수 있다.따라서 모든 정규 그래프를 재구성할 수 있다.^[15]
• 헥스 게임은 두 명의 플레이어가 플레이어를 플레이하는데, 플레이어가 플레이어의 한쪽에서 다른 쪽으로 인접한 피스의 연결 경로를 가질 때까지 헥사곤으로 평행그램 모양의 보드 타일 위에 자신의 색 조각을 배치한다.그것은 결코 무승부로 끝날 수 없다: 보드가 조각들로 완전히 채워질 때쯤에는 선수들 중 한 명이 승리할 수 있는 길을 형성하게 될 것이다.이것에 대한 하나의 증거는 꽉 찬 게임판에서 그래프를 형성하는데, 16진법의 모서리에 정점이 있고, 두 플레이어의 색을 구분하는 16진법의 가장자리가 있다.이 그래프는 보드 모서리에 4개의 홀수 정점이 있고, 다른 곳에 정점이 있기 때문에 반드시 두 모서리를 연결하는 경로를 포함해야 하며, 이것은 반드시 한쪽 측면에 한 명의 플레이어가 승리하는 경로를 가지고 있다.^[16]

증명

오일러의 학위 합계 공식에 대한 증거는 이중 계수 기법을 사용한다: 그는 e ${\displaystyle e}$이(가) 에지이고$$ $꼭지점{\displaystyle }$ v ${\displaystyle v}$이($가)$ 끝점 중 하나인 사건$$ 쌍$({\displaystyle v}$, ${\displaystyle e}$) ${\displaystyle v}$의 수를 두 가지 다른 방법으로 계산한다.꼭지점 $v{\displaystyle }$ ${\$$displaystyle$ $v}$은(는) ${\displaystyle \mathrm{deg}}$ ${\displaystyle (}$${\displaystyle v}$${\displaystyle }$) ${\displaystyle$ $\deg(v$$)}$ 쌍에$$ 속하며$$, 여기서 $\deg($$v)$는 발생되는 가장자리 수입니다$.$따라서 사건 쌍의 수는 각도의 합이다.단, 그래프의 각 에지는 정확히 두 개의 사건 쌍에 속하므로 사건 쌍의 수는 2 ${\displaystyle E}$ $displaystyle$2$E$}이다$.$ 이 두 공식은 동일한 객체 집합을 계산하므로 동일한 값을 가져야 한다.같은 증거는 그래프의 입사 행렬의 항목을 두 가지 방법으로 합친 것으로 해석할 수 있는데, 도 합계를 얻기 위해 행을, 가장자리 수를 두 배로 얻기 위해 열을 사용한다.^[5]

그래프의 경우 핸드셰이킹 보조정리법은 도합 공식의 산술로서 다음과 같다.^[8]정수의 합에서, 합계의 균등성은 합계의 짝수 항에 영향을 받지 않는다. 전체 합은 짝수 항이 있을 때에도, 홀수 항이 있을 때에도, 홀수 항이 있을 때에도 홀수다.도합 공식의 한쪽은 짝수 $2{\displaystyle \mathrm{}}$ $displaystyle$2$$E$}}$이므로$,$ 다른 한쪽의 합은 짝수 수의 홀수 항을 가져야 한다. 즉, 짝수 수의 홀수 도 정점이 있어야 한다.^[5]

대안 또는 직접적으로odd-degree vertices의 숫자는, 주어진 그래프에서 동시에, 그것의 끝점들의 학위를 이 제거의 odd-de의 숫자의 패리티에 영향을 결정할 사건 분석을 사용하여 한쪽 끝을 제거함으로써 증명하기 위해 정도 합 formula,[2]을 증명하기 위해 수학적 귀납 법 사용이 가능하다..정점^[17]

그래프의 특수 클래스에서

정규 그래프

도합 공식은 $정점$이 $n{\displaystyle }$ ${\displaystyle n}$인 $모든$ r ${\displaystyle$ n$}$ -정규$$ 그래프에 $n{\displaystyle }$ ${\displaystyle r}$/ ${\displaystyle 2\mathrm{}}$ ${\displaystyle nr/2}$에지가$$ 있음을 의미한다.^[18]가장자리 수는 정수여야 하므로 $r{\displaystyle }$ ${\displaystyle r}$이(가) 홀수일 때 정점 수는 짝수여야 한다.^[19]$또한{\displaystyle }$, r$${\$displaystyle$r$\}$의 홀수 값에 대해 가장자리 $수$는 r$${\$displaystyle$ r$}$로 구분되어야 한다$.$^[20]

초당적 그래프 및 이항 그래프

초당적 그래프는 그 정점을 두 개의 부분 집합으로 분할하고, 각 가장자리는 각 부분 집합에 하나의 끝점을 가진다.각 부분 집합에서 도 합은 그래프에 있는 가장자리 수와 같다는 동일한 이중 계수 인수를 따른다.특히 두 하위 집합의 도합은 같다.^[21]이선형 그래프의 경우, 정점의 파티션이 $부분{\displaystyle {}_{}}$ 집합 ${\displaystyle {V\mathrm{}}_{}}$ ${\displaystyle 1_{}}$${\$ ${\displaystyle V_{}}$ 2${\$ $V_{i}$의 모든 꼭지점이$$ $r{\displaystyle {}_{}}$ i ${\$인 경우 V ${\displaystyle 1{}_{}{}_{}{r\mathrm{}}_{}}$ = ${\displaystyle V{}_{}}$ 2 ${\displaystyle {r\mathrm{}}_{}}$ 2$}$이어야 한다$.$${\displaystyle V_{1} r_{1}= V_{2} r_{2$}}$$: 둘 다 에지 수가 같다.^[22]

무한 그래프

핸드셰이킹 보조정리기는 한정된 수의 홀수도 정점만 가지고 있는 경우에도 무한 그래프에 통상적인 형태로는 적용되지 않는다.예를 들어, 하나의 끝점이 있는 무한 경로 그래프는 정점 수가 짝수인 대신 홀수 도 정점 하나만 가지고 있다.단, 두 개의 광선을 각 광선으로부터 무한히 많은 정점을 이용하는 제3의 광선이 존재하는 경우, 2개의 광선을 동등한 것으로 간주하는 반무한 경로("레이")의 등가 등급인 끝의 개념을 이용하여 악수하는 보조마 버전을 공식화할 수 있다.단부의 정도는 단부가 포함하는 가장자리-분리선의 최대 수이며, 단부는 그 정도가 유한하고 홀수인 경우 홀수다.보다 일반적으로, 모든 정점이 유한한 그래프에서 끝이 홀수 또는 짝수로 정의될 수 있다.그런 다음, 그러한 그래프에서, 함께 추가된 홀수 정점과 홀수 끝의 수는 짝수 또는 무한대다.^[23]

서브그래프

By a theorem of Gallai the vertices of any graph can be decomposed as ${\displaystyle V=V_{e}\cup V_{o}}$ where ${\displaystyle G(V_{e})}$ has all degree even and ${\displaystyle G(V_{o})}$ has all degree odd with ${\displaystyle V_{o} }$ even by the handshak보조 보조정리In 1994 Yair Caro^[24] proved that ${\displaystyle V_{o} / V >1/{\sqrt {n}}}$ and in 2021 a preprint by Ferber Asaf and Michael Krivelevich showed that ${\displaystyle V_{o} / V >1/10000}$.^[25][26]

계산 복잡성

조합 구조의 존재를 증명하기 위한 교환 그래프 방법과 관련하여, 이러한 구조들이 얼마나 효율적으로 발견될 수 있는지 물어보는 것이 관심이다.예를 들어, 입방형 그래프에 해밀턴 사이클을 입력하는 것으로 가정해 보자. 스미스의 정리로부터 두 번째 사이클이 존재한다는 것을 알 수 있다.이 두 번째 사이클을 얼마나 빨리 찾을 수 있을까?파파디미트리오(1994)는 이와 같은 질문의 계산 복잡성을 조사하거나, 암묵적으로 정의된 큰 그래프에서 한 개의 홀수 정점만 주어졌을 때 제2의 홀수 도 정점을 찾는 것이 더 일반적이었다.그는 이와 같은 문제를 캡슐화하기 위해 복잡도 등급 PPA를 정의했다;^[27] 지시된 그래프에 정의된 밀접하게 연관된 등급인 PPAD는 알고리즘 게임 이론에서 상당한 관심을 끌었다. 왜냐하면 내시 균형 계산은 이 클래스에서 가장 어려운 문제와 계산적으로 동등하기 때문이다.^[28]

복잡도 등급 PPA에 대해 완결성이 입증된 연산 문제에는 Sperner의 보조정리^[29] 및 Hobby-Rice 정리에 따른 자원의 공정한 세분화와 관련된 계산 작업이 포함된다.^[30]

메모들