편파(파)
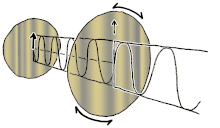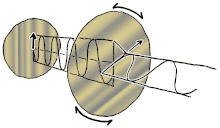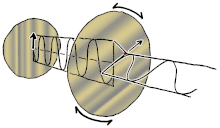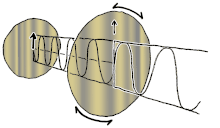
Polarization (waves)편파(편파도)는 [1][2][3][4][5]진동의 기하학적 방향을 지정하는 횡파에 적용되는 특성입니다.횡파에서 진동 방향은 [4]파동의 운동 방향과 수직이다.편광 횡파의 간단한 예로는 팽팽한 줄을 따라 이동하는 진동(이미지 참조)이 있습니다. 예를 들어 기타 현과 같은 악기입니다.현이 어떻게 뽑히느냐에 따라 진동이 수직 방향, 수평 방향 또는 현에 수직인 임의의 각도로 발생할 수 있습니다.반면 액체나 기체 중 음파 등 종파에서는 진동 내 입자의 변위는 항상 전파방향이기 때문에 편파 현상이 나타나지 않는다.편파 현상을 보이는 가로파에는 빛과 전파 등 전자파, 중력파,[6] 고체 중의 가로음파(전단파) 등이 있다.
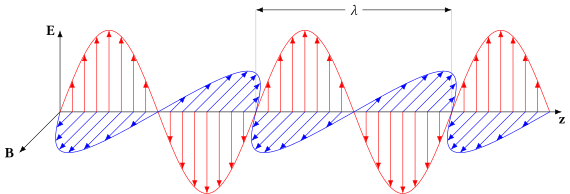
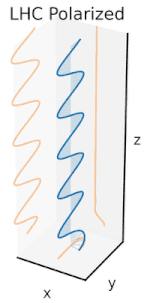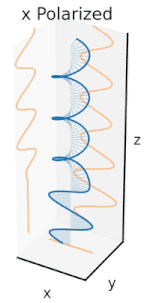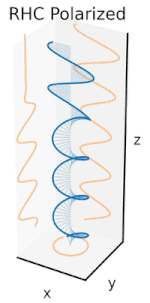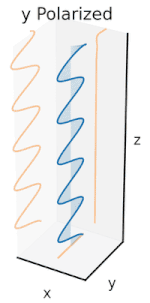
빛과 같은 전자파는 항상 서로 수직인 결합된 진동 전계와 자기장으로 구성되어 있으며, 관례상 전자파의 "편파"는 전계의 방향을 말한다.선형 편파에서는 필드가 단방향으로 진동합니다.원형 또는 타원 편광에서는 파형이 이동할 때 평면에서 필드가 일정한 속도로 회전합니다.회전에는 두 가지 방향이 있을 수 있습니다. 파동 이동 방향에 대해 필드가 우측으로 회전하는 경우 우측 원형 편파라고 하며, 필드가 좌측으로 회전하는 경우 좌측 원형 편파라고 합니다.
태양, 불꽃, 백열등과 같은 많은 광원으로부터의 빛이나 다른 전자기 방사선은 편광의 동일한 혼합을 가진 단파열로 구성되어 있다. 이것은 편광되지 않은 빛이라고 불린다.편광은 편광자를 통해 비편광의 통과를 통해 생성될 수 있으며, 편광자는 편광자가 하나만 통과할 수 있습니다.가장 일반적인 광학 재료는 빛의 편광에 영향을 미치지 않지만 복굴절, 이색성 또는 광학 활동을 보이는 재료는 편광에 따라 다르게 빛에 영향을 미칩니다.이 중 일부는 편광 필터를 만드는 데 사용됩니다.빛은 또한 표면에서 비스듬히 반사될 때 부분적으로 편광됩니다.
양자역학에 따르면 전자파는 광자라고 불리는 입자의 흐름으로도 볼 수 있다.이렇게 볼 때, 전자파의 편광은 [7][8]스핀이라고 불리는 광자의 양자 역학적 특성에 의해 결정됩니다.광자는 두 가지 가능한 스핀 중 하나를 가지고 있다: 광자는 이동 방향에 대해 오른손 감각 또는 왼손 감각으로 회전할 수 있다.원편광 전자파는 오른쪽 또는 왼쪽의 한 가지 유형의 스핀만을 가진 광자로 구성됩니다.직선 편파는 좌우 원편광 상태의 중첩 위치에 있는 광자로 구성되며,[8] 평면에서 진동을 주기 위해 동일한 진폭과 위상이 동기화됩니다.
편광은 광학, 지진학, 전파, 마이크로파 등 횡파를 다루는 과학 분야에서 중요한 변수이다.특히 영향을 받는 것은 레이저, 무선 및 광섬유 통신, 레이더 등의 테크놀로지입니다.
서론
파동 전파 및 편파
대부분의 광원은 공간 특성, 주파수(파장), 위상 및 편광 상태가 다른 임의 혼합 파장으로 구성되기 때문에 일관성이 없고 편광되지 않은(또는 "부분 편광"만) 것으로 분류됩니다.단, 전자파와 편파를 이해하기 위해서는 간섭성 평면파를 고려하는 것이 더 쉽습니다.이것은 특정 방향(또는 파벡터), 주파수, 위상 및 편파 상태의 사인파입니다.특정 공간구조를 가진 파형은 평면파(이른바 각도 스펙트럼)의 조합으로 분해될 수 있기 때문에 평면파에 관한 광학계의 특성화를 사용하여 보다 일반적인 경우에 대한 응답을 예측할 수 있다.비일관성 상태는 주파수(스펙트럼), 위상 및 편광의 분포와 상관없는 파형의 가중 조합으로 확률적으로 모델링할 수 있다.
가로 전자파
자유 공간 또는 다른 균질 등방성 비감쇠 매체를 이동하는 전자파(예를 들어 빛)는 횡파로 적절하게 설명되며, 이는 평면파의 전계 벡터 E와 자기장 H가 각각 파동 전파 방향에 수직(또는 "횡")인(또는 "횡") 방향임을 의미한다. E와 H는 파동 전파 방향이다.lso는 서로 수직이다.관례상 전자파의 '편파' 방향은 그 전계 벡터에 의해 주어진다.광주파수 f의 단색 평면파(진공파장 θ의 빛은 f = c/colm, 여기서 c는 빛의 속도)를 고려하여 전파 방향을 z축으로 한다.Ez = Hz = 0. 복잡한(또는 단계적) 표기법을 사용하여 순간 물리 전기장과 자기장은 다음 방정식에서 발생하는 복잡한 양의 실제 부분에 의해 주어진다.시간 t 및 공간 위치 z의 함수로서(+z 방향의 평면파의 경우 필드가 x 또는 y에 의존하지 않으므로) 이러한 복잡한 필드는 다음과 같이 쓸 수 있습니다.
그리고.
여기서 δ = δ0/n은 매질 내의 파장(굴절률은 n), T = 1/f는 파동의 주기이다.여기서x e, ey, hx, h는y 복소수입니다.보다 콤팩트한 두 번째 형태에서는 이들 방정식이 관습적으로 표현될 때, 이러한 인자는 파수 / 0 {{ k n _ 및 각 주파수(또는 "라디안 주파수") f { f를 사용하여 보다 일반적인 전파를 사용하여 설명된다.+z 방향으로 이동하면 공간 의존성 kz가 k {ot {r}로 됩니다. 서 k {\{k}}은 파동 벡터(\displaystyle {라고 하며, 그 크기는 파동 벡터입니다.
따라서 선행 벡터 e와 h는 각각 파형의 x 및 y 편파 성분의 진폭과 위상을 설명하는 최대 2개의 0이 아닌(복잡한) 성분을 포함합니다(또한 +z 방향의 횡파에 대한 z 편파 성분은 존재할 수 없습니다).특성 임피던스 {\를 갖는 특정 매체에 대해 h는 다음과 같이 e와 관련됩니다.
그리고.
- x - y {\{}=-{\
유전체에서 θ는 실재하고 값 θ0/n을 가진다.여기서 n은 굴절률, θ는0 자유공간의 임피던스이다.전도 매체에서는 임피던스가 복잡해집니다.[clarification needed]이 관계를 고려할 때 E와 H의 도트곱은 [dubious ]0이어야 합니다.
이러한 벡터가 예상대로 직교(서로 직각)임을 나타냅니다.
따라서 전파 방향(+z)과 θ를 알면 전계를 나타내는 e와x e로y 파형을 지정할 수 있습니다.e와y e를 포함하는x 벡터(단, 가로파의 경우 반드시 0인 z 성분이 없음)를 존스 벡터라고 합니다.파형의 편광 상태를 지정하는 것 외에 일반 Jones 벡터는 파형의 전체 규모와 위상을 규정합니다.특히 광파의 세기는 두 가지 전계 구성요소의 크기 제곱합에 비례합니다.
그러나 파형의 편광 상태는 e 대 e의yx (복잡한) 비율에만 의존합니다.따라서y e + e = 1인 파형을x 생각해 보겠습니다. 이는 빈 ( ( \ } \ _에서 평방미터당 약 .00133와트의 강도에 해당합니다.그리고 편광 상태를 논할 때 파형의 절대 위상은 중요하지 않으므로 e의x 위상은 0, 즉x e는 실수이고y e는 복잡할 수 있다고 하자.이러한 제한 하에서 e와y e는 다음과x 같이 나타낼 수 있습니다.
여기서 편광 상태는 Q 값(-1 < Q < 1) 및 상대 위상{\(\에 의해 완전히 파라미터화 됩니다.
비횡파
진동은 전파방향에 수직인 방향으로 한정되지 않는 파동도 많다.이러한 사례는 가로파(벌크 미디어의 대부분의 전자파 등)에 초점을 맞춘 현재 기사의 범위를 훨씬 벗어나지만, 방금 한 것처럼 Jones 벡터를 사용하여 간섭파의 편파를 간단히 설명할 수 없는 경우에 유의해야 한다.
전자파를 고려하면 앞에서 설명한 내용은 균일한 등방성 비감쇠 매체의 평면파에 엄격하게 적용되는 반면, 비등방성 매체의 경우(아래에서 설명한 복굴절 결정 등) 전기장 또는 자기장은 종방향 및 횡방향 구성요소를 가질 수 있다.이 경우 전기변위 D 및 자속밀도[clarification needed] B는 여전히 상기 형상을 따르지만 현재 텐서에 의해 주어진 전기자화율(또는 자기투과율)의 이방성 때문에 E(또는 H)의 방향이 D(또는 B)의 방향과 다를 수 있다.등방성 매체에서도 굴절률이 [clarification needed]금속과 같은 유의한 가상 부분(또는 "소멸 계수")을 가진 매체에 소위 비균질파가 발사될 수 있다. 이러한 장은 엄밀하게 [9]: 179–184 [10]: 51–52 횡단되지도 않는다.도파관(광섬유 등)에서 전파되는 표면파 또는 파형은 일반적으로 횡파가 아니라 전기 또는 자기 횡파 모드 또는 하이브리드 모드라고 할 수 있습니다.
빈 공간에서도 평면파 근사가 파괴되는 초점 영역에서 종계 성분을 발생시킬 수 있다.극단적인 예는 각각 전기장 또는 자기장이 (전파 [11]방향을 따라) 완전히 세로인 방사 또는 접선 편광이다.
유체중의 음파등의 종파의 경우, 진동의 방향은 당연히 진행 방향을 따르는 것이기 때문에, 편광의 문제는 통상은 언급조차 되지 않는다.한편, 벌크 고체 내의 음파는 총 3개의 편파 성분으로 종방향뿐만 아니라 횡방향도 가능하다.이 때 횡편파는 전단응력 및 전파방향과 수직방향으로의 변위방향과 관련지어지며, 종편파는 고체의 압축과 전파방향에 따른 진동을 나타낸다.지진학에서는 가로편광과 세로편광의 차분포가 중요하다.
편광 상태
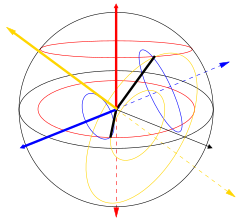
편광은 처음에는 순수한 편광 상태와 일부 광학 주파수에서 일관된 사인파만 고려함으로써 가장 잘 이해할 수 있습니다.인접 다이어그램의 벡터는 단일 모드 레이저에서 방출되는 전계의 발진을 설명할 수 있습니다(발진 주파수는 일반적으로15 10배 빠릅니다).필드는 페이지를 따라 x-y 평면에서 진동하며 파형은 페이지에 수직인 z 방향으로 전파됩니다.아래의 처음 두 그림은 두 가지 다른 방향에서 선형 편광을 위해 전체 사이클에 걸쳐 전계 벡터를 추적합니다. 이들은 각각 다른 편광 상태(SOP)로 간주됩니다.45°에서의 선형 편파는 수평 직선 편파(맨 왼쪽 그림처럼)와 같은 위상에서의 수직 편파의 추가로도 볼 수 있습니다.
이러한 수평 편광 성분과 수직 편광 성분 사이에 위상 변화를 도입하면 세 번째 그림과 같이 일반적으로 타원 편광을[12] 얻을 수 있습니다.위상 편차가 정확히 ±90°이면 원형 편파가 발생합니다(4번째 및 5번째 그림).따라서 실제로는 선형 편광에서 시작하여 1/4파 플레이트를 사용하여 위상 편광을 도입하는 원형 편광입니다.두 개의 위상 편이 성분이 회전 전계 벡터를 발생시킨 결과는 오른쪽 애니메이션에 나와 있습니다.원형 또는 타원 편광은 필드의 시계 방향 또는 시계 반대 방향 회전을 수반할 수 있습니다.이는 위의 두 원형 편광과 같은 뚜렷한 편광 상태에 해당합니다.
물론 이 설명에서 사용되는 x축과 y축의 방향은 임의입니다.이러한 좌표계를 선택하고 편광 타원을 x 및 y 편광 성분으로 보는 것은 이러한 기저 편광의 관점에서 Jones 벡터의 정의에 해당합니다.일반적으로 x가 입사 평면에 있는 것과 같은 특정 문제에 적합하도록 축을 선택합니다.입사 평면(p 및 s 편파, 아래 참조)과 직교하는 선형 편파에는 별도의 반사 계수가 있기 때문에 이 선택은 표면으로부터의 파동 반사의 계산을 크게 단순화합니다.
또한, 기본 함수로 선형 편광뿐만 아니라 직교 편광 상태의 모든 쌍을 사용할 수 있습니다.예를 들어, 오른쪽과 왼쪽의 원형 편광을 기저 함수로 선택하면 원형 복굴절(광학적 활동) 또는 원형 이색성과 관련된 문제의 해법을 단순화할 수 있다.
편광 타원
순수하게 편광된 단색파를 생각해 봅시다.만약 한 진동 사이클에 걸쳐 전계 벡터를 플롯한다면, 일반적으로 타원 편광의 특정 상태에 해당하는 타원을 얻을 수 있을 것이다.선형 편광과 원형 편광은 타원 편광의 특수한 경우로 볼 수 있습니다.
편광 상태는 타원의 기하학적 파라미터와 그 "핸드니스" 즉, 타원을 중심으로 한 회전이 시계방향인지 반시계방향인지에 대해 기술할 수 있다.타원도형의 파라미터화 중 하나는 타원률 θ = a/b와 함께 타원장축과 X축[13] 사이의 각도로 정의되는 방향각 θ를 타원장축과 [14][15][16]단축의 비율로 규정한다.(축 비라고도 함)타원의 별남 e의 타원율 변수는 대안적인 parameterization=1− b2/2,{\textstyle e={\sqrt{1-b^{2}{2}}},}또는 타원 모양 각도,χ)arctan b/{\textstyle\chi=\arctan b/a})arctan 1/ε{\textstyle 1/\varepsilon=\arctan}은 그림에 나타나 있다.[13]각도 θ는 또한 푸앵카레 구(아래 참조)에 표시된 편광 상태의 위도(적도로부터의 각도)가 ±2µ와 동일하다는 점에서 유의하다.선형편광과 원형편광의 특수한 경우는 무한대 및 일체성의 타원성 θ(0과 45°의 θ)에 해당한다.각각 다음과 같다.
존스 벡터
완전 편광 상태에 대한 완전한 정보는 편광면 내 전계 벡터의 2개 성분에서의 진동 진폭과 위상에 의해서도 제공된다.이 표현은 편광의 다른 상태가 어떻게 가능한지를 보여주기 위해 위에서 사용되었습니다.진폭 및 위상 정보는 2차원 복소 벡터(Jones 벡터)로 편리하게 나타낼 수 있습니다.
서 1 a_과 2는 전계 벡터의 2개 성분에서 파형의 진폭을 나타내고 1 _})과 2(\ _는 위상을 나타냅니다.단위계수가 복소수인 존스 벡터의 곱은 같은 타원을 나타내는 다른 존스 벡터를 제공하므로 편광 상태가 같다.물리 전장은 존스 벡터의 실제 부분으로서 변화하지만 편광 상태 자체는 절대 위상과는 독립적입니다.존스 벡터를 나타내기 위해 사용되는 기저 벡터는 선형 편광 상태를 나타낼 필요가 없다(즉, 실재한다).일반적으로 직교 벡터 쌍이 0의 내적을 갖는 것으로 정식으로 정의되는 2개의 직교 상태를 사용할 수 있다.일반적인 선택은 좌우 원형 편파이다. 예를 들어 원형 복굴절 매체(아래 참조) 또는 원형 편파에 민감한 간섭성 검출기의 신호 경로에서 이러한 두 가지 구성요소의 파동 전파를 모델링하는 것이다.
좌표 프레임
편광 상태가 기하학적 파라미터와 존스 벡터를 사용하여 표현되든 상관없이 파라미터화에서 암묵적으로 나타나는 것은 좌표 프레임의 방향이다.이것은 어느 정도의 자유도, 즉 전파 방향에 대한 회전을 가능하게 한다.지구 표면과 평행하게 전파되는 빛을 고려할 때, "수평"과 "수직" 편광이라는 용어가 종종 사용되며, 전자는 존스 벡터의 첫 번째 성분, 즉 0 방위각과 관련이 있습니다.한편, 천문학에서는 적도 좌표계가 일반적으로 사용되며, 정북에 대응하는 제로 방위각(또는 수평 좌표계와 혼동을 피하기 위해 천문학에서 더 일반적으로 부르는 위치 각도)이 사용됩니다.
s 및 p 지정
자주 사용되는 또 다른 좌표계는 입사면과 관련이 있다.이것은 들어오는 전파 방향과 계면의 평면에 수직인 벡터, 즉 반사 또는 굴절 전후에 광선이 이동하는 평면에 의해 만들어진 평면입니다.이 평면에 평행한 전계의 성분을 p-라이크(병렬)라고 하고, 이 평면에 수직인 성분을 s-라이크(senkrecht, 독일어로 수직인 경우)라고 한다.따라서 입사면을 따라 전기장이 있는 편광은 p편광이라고 하며, 입사면에 대해 전기장이 정규인 빛은 s편광이라고 한다.P 편광은 일반적으로 횡자기(TM)라고 불리며 pi 편광 또는 접선 평면 편광이라고도 불립니다.S편광은 가로-전기(TE)라고도 하며 시그마 편광 또는 시상면 편광이라고도 합니다.
편광되지 않은 부분 편광
이 섹션에는 문서의 다른 부분에서 반복되거나 중복되는 내용이 포함될 수 있습니다.유사한 텍스트를 병합하거나 반복된 문장을 삭제하여 개선하십시오.(2014년 7월) |
정의.
대부분의 다른 일반적인 가시광선원과 마찬가지로 자연광은 일관성이 없다: 방사선은 상관 없고 일반적으로 무작위 편광으로 방출되는 많은 원자 또는 분자에 의해 독립적으로 생성된다.이 경우 빛은 비편광이라고 합니다.이 용어는 어느 한 지점에서든 전기장과 자기장에 대한 명확한 방향이 있기 때문에 다소 부정확하지만, 편광은 시간에 따라 매우 빠르게 변하기 때문에 측정되거나 실험 결과와 관련이 없을 것입니다.이른바 탈편광기는 편광된 빔에 작용하여 실제로 모든 지점에서 완전히 편광된 빔을 생성하지만, 이 빔에서 편광은 너무 빠르게 변화하여 의도된 용도에서는 무시될 수 있습니다.
편광되지 않은 빛은 두 개의 독립된 반대편광 스트림의 혼합으로 설명할 수 있으며, 각각 [17][18]강도는 절반입니다.이러한 스트림 중 하나에 전력이 다른 스트림보다 많을 때 빛은 부분적으로 편광된다고 합니다.특정 파장에서 부분 편광은 완전 비편광 성분과 완전 편광 [19]: 330 성분의 중첩으로 통계적으로 기술할 수 있다.그런 다음 편광의 정도와 편광 성분의 매개변수로 빛을 설명할 수 있습니다.편광 성분은 위에서 설명한 바와 같이 존스 벡터 또는 편광 타원으로 설명할 수 있습니다.그러나 편광의 정도를 설명하기 위해 일반적으로 Stokes 파라미터(아래 참조)를 사용하여 편광 [19]: 351, 374–375 상태를 지정합니다.
동기
균질 매체를 통한 평면파의 전달은 존스 벡터와 2×2 존스 행렬의 관점에서 완전히 설명된다.그러나 실제로는 공간의 불균일성이나 상호 간섭성이 없는 파동의 존재로 인해 모든 빛을 그렇게 단순하게 볼 수 없는 경우가 있다.예를 들어 이른바 탈분극은 존스 행렬을 사용하여 설명할 수 없습니다.이러한 경우에는 Stokes 4-벡터에 작용하는 4×4 매트릭스를 사용하는 것이 일반적입니다.이러한 행렬은 1929년 폴 솔레트에 의해 처음 사용되었지만, 뮐러 행렬로 알려지게 되었다.모든 존스 행렬에는 뮐러 행렬이 있지만, 그 반대는 사실이 아닙니다.그런 다음 [19]: 377–379 뮐러 행렬을 사용하여 복잡한 표면 또는 입자의 앙상블에서 파장이 산란될 때 관찰된 편광 효과를 설명한다.
연속성 행렬
존스 벡터는 단일 단색파의 편광 상태와 위상을 완벽하게 묘사하며, 위에서 설명한 바와 같이 순수한 편광 상태를 나타냅니다.그러나 서로 다른 편파(또는 다른 주파수)의 파형 혼합은 Jones 벡터에 해당하지 않습니다.소위 부분 편광 방사선의 경우, 전기장은 확률적이며, 전기장의 성분들 사이의 변동과 상관관계는 통계적으로만 설명할 수 있다.이러한 표현 중 하나가 일관성 [20]: 137–142 매트릭스입니다.
여기서 각도 괄호는 여러 파형 주기에 걸쳐 평균을 나타냅니다.일관성 매트릭스의 몇 가지 변형이 제안되었다. 비너 일관성 매트릭스와 리처드 바라캣의 스펙트럼 일관성 매트릭스는 신호의 스펙트럼 분해의 일관성을 측정하는 반면 울프 일관성 매트릭스는 모든 시간/주파수에 걸쳐 평균적이다.
일관성 행렬에는 편광에 대한 모든 2차 통계 정보가 포함됩니다.이 행렬은 공명행렬의 고유 벡터에 대응하는 2개의 등가행렬의 합으로 분해될 수 있으며, 각각은 서로 직교하는 편광 상태를 나타냅니다.대체 분해는 완전히 편광된(결정식 0) 성분과 비편광화된(스케일링된 동일 매트릭스) 성분으로 이루어진다.어느 경우든 성분을 합산하는 동작은 두 성분으로부터의 파동의 일관되지 않은 중첩에 대응한다.후자의 경우는 "편광도"의 개념을 야기한다. 즉, 완전한 편광 성분에 의해 기여되는 총 강도의 비율이다.
Stokes 파라미터
코히렌시 매트릭스는 시각화하기가 쉽지 않기 때문에 총 강도(I), (분할) 편파도(p) 및 편파 타원의 형상 매개변수로 일관되지 않거나 부분적으로 편파된 방사선을 설명하는 것이 일반적이다.대체적이고 수학적으로 편리한 설명은 1852년 조지 가브리엘 스톡스에 의해 도입된 스톡스 매개변수에 의해 제공됩니다.Stokes 파라미터와 명암 및 편광 타원 파라미터의 관계는 아래 방정식과 그림에 나와 있습니다.
여기서 Ip, 2θ 및 2θ는 마지막 3개의 Stokes 파라미터의 3차원 공간에서의 편광 상태의 구면 좌표이다.편광 타원이 180° 회전하는 것과 90° 회전하는 것을 동반하는 반축 길이와 구별이 안 된다는 사실에 각각 θ 및 θ 앞의 2개의 계수를 주목한다.Stokes 파라미터는 I, Q, U 및 V로 표시될 수 있습니다.
4개의 Stokes 매개변수는 근축파의 2D 편파를 설명하기에 충분하지만 일반적인 비근축파나 증발장의 [21][22]3D 편파를 설명하지는 않습니다.
푸앵카레 구
첫 번째 Stokes 매개변수0 S(또는 I)를 무시하면 다른 세 개의 Stokes 매개변수를 3차원 데카르트 좌표로 직접 플롯할 수 있습니다.편광 컴포넌트 내 특정 전력에 대해
모든 편광 상태의 집합은 첨부 다이어그램에 표시된 것처럼 이른바 Poincaré 구(단 반지름 P) 표면의 점에 매핑된다.
종종 총 빔 파워는 관심이 없으며, 이 경우 스토크스 벡터를 총 강도0 S로 나누어 정규화된 스토크스 벡터가 사용됩니다.
정규화된 Stokes Sδ(\는 단일 파워( 0 \ S}=를 가지며, 3차원으로 표시된 3개의 유의한 Stokes 파라미터는 순수 편광 상태(\ 에 놓입니다부분 편광 상태는 원점에서 P S 2 + 22 + 32 ({ P'= 2}'^{2}'+}'^2}'^{2}'^{2}'^{2}'^{2}'^{2}'^{2}'^{2}'s}'^{2}'^{2}'^{2}'^{{2}'}'s}'ss}'s)의 에 있는 거리에 있는 푸앵카레 구편광되지 않은 성분이 관심 없을 때 스토크스 벡터는 다음을 얻기 위해 더욱 정규화될 수 있다.
이 점이 플롯되면 단일 반지름 푸앵카레 구의 표면에 위치하여 편광 성분의 편광 상태를 나타냅니다.
Poincaré 구면상의 두 개의 대척점은 직교 편광 상태를 나타냅니다.두 편광 상태 간의 중첩은 구를 따라 위치 사이의 거리에 따라 달라집니다.순수한 편광 상태가 구체에 매핑될 때만 참이 될 수 있는 이 특성은 푸앵카레 구의 발명과 스토크스 매개변수의 사용의 동기이며, 그 위에 (또는 아래에) 표시된다.
IEEE에서는 RHCP와 LHCP를 물리학자용과 반대로 정의하고 있습니다.IEEE 1979 안테나 표준은 푸앵카레 구의 남극에 RHCP를 표시합니다.IEEE는 오른손을 사용하여 RHCP를 정의하고 엄지손가락은 전송 방향을 가리키며 손가락은 E 필드의 회전 방향을 시간에 따라 나타냅니다.물리학자 및 엔지니어가 사용하는 반대 규칙의 근거는 천체관측이 항상 관찰자를 향해 이동하는 들어오는 파동으로 이루어지기 때문입니다. 대부분의 엔지니어의 경우, 그들은 송신기 뒤에 서서 그들로부터 멀어지는 파동을 지켜보고 있는 것으로 추정됩니다.이 문서에서는 IEEE 1979 안테나 표준을 사용하지 않으며 IEEE 작업에서 일반적으로 사용되는 +t 표기법을 사용하지 않습니다.
반사 및 전파에 미치는 영향
파동 전파에서의 편파
진공상태에서는 전계성분이 빛의 속도로 전파되기 때문에 편광상태는 변화하지 않지만 시공간에서 파상의 위상이 변화한다.즉, +z 방향의 평면파의 전계 벡터 e는 다음과 같습니다.
여기서 k는 wavenumber 입니다.이상과 같이 순간전장은 Jones 벡터의 e - i t{ - \ t} 곱의 실제 부분이며, 전자파가 물질과 상호작용할 때 물질의 (복잡한) 굴절률에 따라 전파가 변화한다.굴절률의 실제 또는 가상의 부분이 파형의 편광 상태, 복굴절 및 편광 이분법(또는 감쇠)으로 알려진 특성에 따라 달라지면 파형의 편광 상태는 일반적으로 변경됩니다.
이러한 매체에서 임의의 편파 상태를 가진 전자파는 서로 다른 전파 상수와 조우하는 2개의 직교 편파 성분으로 분해될 수 있다.주어진 경로를 통한 전파의 영향은 존스 행렬로 알려진 복잡한 2×2 변환 행렬 J의 형태로 가장 쉽게 특징지어집니다.
투명한 물질을 통과하는 것으로 인한 존스 행렬은 복굴절뿐만 아니라 전파 거리에 따라 달라집니다.복굴절률(및 평균 굴절률)은 일반적으로 분산되며, 즉 광학 주파수(파장)의 함수에 따라 달라집니다.그러나 비복굴절 재료의 경우 2×2 Jones 행렬은 (스칼라 위상 인자와 감쇠 인자를 곱한) 항등 행렬이며, 이는 전파 중 편광의 변화가 없음을 의미한다.
두 직교 모드의 전파 효과의 경우, Jones 행렬은 다음과 같이 쓸 수 있습니다.
여기서1 g와2 g는 위상 지연 및 두 편파 고유 모드의 전파로 인한 진폭 감쇠를 설명하는 복소수입니다.T는 이러한 전파모드에서 존스 벡터에 사용되는 선형계로의 기저변화를 나타내는 유니터리 매트릭스입니다.선형 복굴절 또는 감쇠의 경우 모드 자체가 선형 편광 상태이므로 좌표축이 적절히 선택되면 T와−1 T를 생략할 수 있습니다.
복굴절
미디어 복굴절은 진폭지만 미분 위상 지연 발생한다 변화했다, 존스 매트릭스 유니터리 행렬:1)g2 = 1. 미디어는 에르 미트 행렬의.를 사용하여 설명할 수 있을 것은 두 사람의 편광의 진폭 달리 영향을 받는다(또는 양극화의 의미에서 이색의), diattenuating했다.matrix(표준에 공통 위상 인자를 곱한 값).사실, 어떤 행렬도 유니터리 행렬과 양의 에르미트 행렬의 곱으로 쓰여질 수 있기 때문에, 편광의존 광학 컴포넌트의 배열에 의한 빛의 전파는 이 두 가지 기본적인 변환의 곱으로 쓰여질 수 있다.
복굴절 미디어에서는 감쇠는 이루어지지 않지만 2가지 모드에서는 위상 지연이 발생합니다.선형 복굴절의 잘 알려진 징후(즉, 기저 편광은 직교 선형 편광)는 광파판/리타더 및 많은 결정에서 나타난다.직선 편광 빛이 복굴절 물질을 통과하면 편광 방향이 기본 편광 중 하나와 동일하지 않는 한 편광 상태는 일반적으로 변화합니다.위상변화와 편광상태의 변화는 보통 파장에 의존하기 때문에 두 편광자 사이의 백색광 아래에서 볼 수 있는 물체는 첨부된 사진에서 볼 수 있듯이 다채로운 효과를 낼 수 있다.
원형 복굴절은 광학 활동이라고도 하며, 특히 키랄 유체의 경우 전파 방향을 따라 자기장이 존재하기 때문에 패러데이 회전이라고 합니다.직선 편광 빛이 이러한 물체를 통과할 때, 편광의 축이 회전한 상태에서 여전히 직선 편광을 방출합니다.선형 복굴절과 원형 복굴절의 조합은 두 개의 직교 타원 편광을 기본으로 갖습니다. 그러나 "엘리펙탈 복굴절"이라는 용어는 거의 사용되지 않습니다.
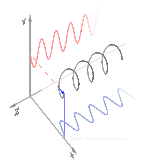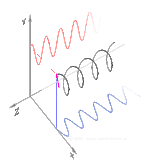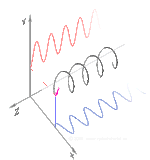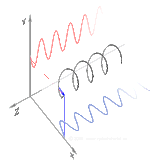
이러한 모드에 대해 45° 각도로 들어오는 파형이 선형 편광된 선형 복굴절(2개의 직교 선형 전파 모드 포함)의 경우를 시각화할 수 있습니다.차분 위상이 축적되기 시작하면 편광은 타원형이 되어 최종적으로 순수하게 원형 편광(90° 위상차)으로 변화하고, 그 후 원래의 편광에 수직인 타원형 및 선형 편광(180° 위상)으로 변화하며, 다시 원형(270° 위상)을 거쳐 원래의 방위각과 타원형으로 변화한다.각도를 조정하고 최종적으로 사이클이 다시 시작되는 원래의 선형 편광 상태(360° 위상)로 돌아갑니다.일반적으로 상황은 더 복잡하며, 전파 모드에 의해 정의된 축을 중심으로 푸앵카레 구가 회전하는 것으로 특징지을 수 있습니다.왼쪽 그림에 선형(파란색), 원형(빨간색) 및 타원(노란색) 복굴절의 예가 나와 있습니다.편광의 총 강도와 정도는 영향을 받지 않는다.복굴절 매체의 경로 길이가 충분한 경우, 시준된 빔(또는 광선)의 두 편광 구성요소는 최종 전파 방향이 동일하더라도(입구면과 출구면이 평행하다고 가정함) 위치 오프셋으로 재료를 빠져나갈 수 있습니다.이것은 일반적으로 석회석 결정을 사용하여 볼 수 있으며, 이 결정 뒤에 있는 물체의 두 개의 약간 오프셋된 이미지를 시청자에게 제공합니다.1669년 에라스무스 바르톨리누스에 의해 분극의 첫 발견을 제공한 것은 바로 이 영향이었다.
이분법
한쪽 편광 모드의 전송이 우선적으로 감소하는 미디어를 이분법 또는 디어터닝이라고 합니다.복굴절과 마찬가지로 탈감쇠는 선형 편광 모드(결정 내) 또는 원형 편광 모드(일반적으로 액체 내)에 관한 것일 수 있습니다.
한 모드에서 거의 모든 방사선을 차단하는 장치를 편광 필터 또는 단순히 "편광자"라고 합니다.이는 위의 Jones 행렬 표현에서 g=0에 해당합니다2.이상적인 편광자의 출력은 편광 모드에서 입력파의 원래 진폭과 동일한 진폭을 갖는 특정 편광 상태(일반적으로 선형 편광)입니다.다른 편광 모드에서의 전력은 배제됩니다.따라서 편광되지 않은 빛이 이상적인 편광자(g1=1 및2 g=0)를 통과하면 초기 전력의 정확히 절반이 유지됩니다.실용적인 편광자, 특히 저렴한 시트 편광자는 g < 1이 되도록1 추가 손실이 있습니다.그러나 많은 경우 g 대2 g의 비교를1 수반하는 편광자의 편광도 또는 소멸비이다.Jones 벡터는 (강도가 아닌) 파형의 진폭을 의미하기 때문에, 비편광 빛에 의해 조명되었을 때, 불필요한 편광의 나머지 전력은 의도된 편광의 전력의2 (g1/2g)이 됩니다.
거울 반사
연장 매체의 복굴절과 이분법 외에, 존스 매트릭스를 사용하여 설명할 수 있는 편광 효과는 굴절률이 다른 두 재료 사이의 (반사) 계면에서도 발생할 수 있다.이러한 효과는 프레넬 방정식으로 처리됩니다.파형의 일부는 전송되고 일부는 반사된다. 주어진 재료의 경우 그러한 비율(및 반사 위상)은 입사 각도에 따라 달라지며 s와 p 편광에 따라 다르다.따라서 반사광의 편광 상태는 (처음에는 편광되지 않더라도) 일반적으로 변화한다.
p 편광의 반사 계수가 0인 Brewster's angle로 알려진 특별한 입사 각도로 표면에 충돌하는 모든 빛은 s 편광만 남기고 반사된다.이 원리는 소위 "판 편광자 편광자(pile of plate polarizer)"에 적용되며, 이 원리는 각 Brewster 각도 표면에서의 반사에 의해 s 편광의 일부가 제거되고 그러한 많은 표면을 투과한 후 p 편광만 남는다.일반적으로 p 편광의 반사 계수가 작은 것도 편광 선글라스의 기초가 된다. 예를 들어 s(수평) 편광을 차단함으로써 젖은 거리의 반사로 인한 대부분의 눈부심을 제거할 [19]: 348–350 수 있다.
정상 입사 시 반사되는 중요한 특수한 경우(비등방성 물질 포함)에는 특별한 s 또는 p 편광은 없다.x편광성분과 y편광성분은 모두 동일하게 반사되므로 반사파의 편광은 입사파의 편광과 동일하다.그러나 원형(또는 타원형) 편광의 경우, 이는 관례에 따라 전파 방향에 대해 규정되기 때문에 편광 상태의 핸드니스(handdeness)가 반전된다.+z 방향의 파형에 대해 "오른쪽"이라고 불리는 x-y 축 주위의 전기장의 원형 회전은 -z 방향의 파형에 대해 "왼쪽"입니다.그러나 0이 아닌 입사 각도에서 반사를 하는 일반적인 경우에는 그러한 일반화를 할 수 없다.예를 들어, 방목 각도로 유전체 표면에서 반사된 오른쪽 원 편광은 여전히 오른손 편광입니다(그러나 타원형).비정상 입사 시 금속에서 반사된 선형 편광은 일반적으로 타원 편광됩니다.이러한 경우는 및 p 편광 컴포넌트의 다른 프레넬계수에 의해 작용되는 Jones 벡터를 사용하여 처리됩니다.
편광과 관련된 측정 기법
일부 광학 측정 기술은 편광에 기초하고 있습니다.다른 많은 광학 기술에서 편광은 매우 중요하거나 최소한 고려되고 제어되어야 한다. 그러한 예는 언급하기에는 너무 많다.
응력 측정
공학에서 응력유발 복굴절현상은 투명한 재료의 응력을 쉽게 관찰할 수 있게 한다.위에서 언급하고 첨부된 사진에서 볼 수 있듯이 복굴절의 색도는 일반적으로 두 편광자 사이에서 볼 때 컬러 패턴을 생성한다.이것에 의해, 외력이 가해지면, 재료에 기인하는 내부 응력이 관찰된다.또한 제조 시 응력 "동결"로 인해 복굴절이 자주 관찰됩니다.이는 제조 공정에서 재료의 신축으로 인해 복굴절이 발생하는 셀로판 테이프에서 잘 관찰됩니다.
타원 측정법
타원측정법은 균일한 표면의 광학적 특성을 측정하는 강력한 기술이다.이러한 표면에서 반사된 빛에 따른 편광 상태를 측정하는 것이 포함됩니다.이는 일반적으로 입사각이나 파장(또는 둘 다)의 함수로 이루어집니다.타원측정법은 반사에 의존하기 때문에 샘플이 빛에 투명하거나 뒷면이 접근 가능하도록 할 필요는 없다.
타원측정법을 사용하여 벌크 재료 표면의 (복잡한) 굴절률을 모델링할 수 있습니다.또한 기판상에 퇴적된 하나 이상의 박막층의 파라미터를 결정하는 데도 매우 유용하다.반사 특성으로 인해 p와 s 편광 성분의 예측 크기뿐만 아니라 타원계를 사용한 측정과 비교하여 반사 시 상대 위상 변화도 가능합니다.일반 타원계수는 실제 반사계수(조명빔의 광도계수)가 아니라 p와 s 반사의 비율과 연구 대상 표면에 의한 반사에 의해 유도되는 편광 타원성 변화(따라서 이름)를 측정한다.예를 들어,[23]: 585ff [24]: 632 과학과 연구에 사용되는 것 외에, 타원계는 생산 공정을 제어하기 위해 현장에서 사용된다.
지질학
(선형) 복굴절의 특성은 결정질 광물에 널리 퍼져 있으며, 편광의 최초 발견에 중추적인 역할을 했다.광물학에서 이 성질은 광물을 식별하기 위해 편광 현미경을 사용하여 자주 이용된다.상세한 [25]: 163–164 것에 대하여는, 광학 광물학을 참조해 주세요.
고체 물질의 음파는 편파 현상을 보인다.지진학 분야에서는 지구를 통한 세 편파의 차등 전파가 매우 중요하다.수평 및 수직 편파 지진파(전단파)는 SH,[26]: 48–50 [27]: 56–57 SV, 종편파(압축파)는 P파라고 한다.
화학
결정의 복굴절은 그것을 식별하는 데 유용하며, 따라서 선형 복굴절의 검출은 지질학 및 광물학에서 특히 유용하다는 것을 알게 되었다.직선 편광은 일반적으로 이러한 결정을 투과할 때 편광 상태가 변하기 때문에 위의 사진에서 볼 수 있듯이 교차 편광자 두 개 사이에서 볼 때 두드러집니다.마찬가지로 화학에서는 액체용액 중 편광축의 회전이 유용한 측정이 될 수 있다.액체 중 직선 복굴절은 불가능하지만 키랄 분자가 용액 중에 있을 때는 원형 복굴절이 있을 수 있다.그러한 분자의 오른손과 왼손잡이 에난티오머가 같은 수(일명 라세미 혼합물)로 존재할 때, 그들의 효과는 상쇄된다.그러나 유기 분자의 경우와 같이 단 1개(또는 1개의 우세)가 존재할 경우 순원형 복굴절(또는 광학 활성)이 관찰되어 그 불균형의 크기(또는 오직 하나의 엔안티오머가 존재한다고 가정할 수 있는 분자 자체의 농도)가 드러난다.이는 편광된 빛이 액체의 관을 통과하는 편광계를 사용하여 측정되며, 그 끝에는 편광자가 회전하여 빛의 전달을 [19]: 360–365 [28]무효로 합니다.
천문학
천문학의 많은 영역에서, 우주로부터 편광된 전자기 복사에 대한 연구는 매우 중요하다.일반적으로 별의 열복사의 요인은 아니지만, 편광은 간섭성 천문원(예: 수산기 또는 메탄올 매저)과 활동 은하의 큰 전파엽 및 펄서 방사선(추측되거나 때로는 간섭성일 수 있음)에서 발생하는 방사선에도 존재하며, 또한 임포스이기도 하다.성간 먼지에서 흩어지면서 별빛을 바라보게 된다.편광은 방사선과 산란원에 대한 정보를 제공하는 것 외에도 패러데이 [29]: 119, 124 [30]: 336–337 회전을 통해 성간 자기장을 조사합니다.우주 마이크로파 배경의 편광은 초기 우주의 [31][32]물리학을 연구하는 데 사용되고 있다.싱크로트론 방사선은 본질적으로 편광입니다.천문학적인 원천이 [33]지구상의 생물학적 분자의 키라리티를 유발했다는 주장이 제기되어 왔다.
응용 프로그램 및 예시
편광 선글라스
편광되지 않은 빛은 일반적으로 경사진(반사된) 표면에 반사된 후 편광 정도를 얻는다.이 현상은 1808년 수학자 에티엔 루이 말루스에 의해 관찰되었고, 말루스의 법칙은 그의 이름을 따왔다.편광 선글라스는 이 효과를 이용하여 수평 표면, 특히 방목 각도로 전방 도로를 통해 반사되는 눈부심을 감소시킨다.
편광 선글라스를 착용한 사람은 반사 또는 산란에 의한 자연 편광과 함께 강화된 유리(예: 자동차 창문) 또는 투명한 플라스틱으로 만들어진 항목에서 색 의존적 복굴절 효과와 같은 의도치 않은 편광 효과를 가끔 볼 수 있다.LCD 모니터(아래 참조)의 편광은, 모니터의 착용시에 매우 두드러집니다.
하늘의 편광과 사진

분극은 지구의 대기를 통과할 때 에어로졸에 의해 산란된 햇빛 때문에 하늘의 빛에서 관찰된다.산란된 빛은 맑은 하늘에서 밝기와 색을 만들어 냅니다.이렇게 산란된 빛의 부분 편광은 사진을 통해 하늘을 어둡게 하고 대조도를 높이는 데 사용될 수 있습니다.이 효과는 태양과 90° 각도를 이루는 하늘의 지점에서 가장 강하게 관찰된다.편광 필터는 이러한 효과를 사용하여 하늘의 반사 또는 산란이 수반되는 [19]: 346–347 [34]: 495–499 촬영 장면의 결과를 최적화합니다.

하늘 편광은 항법에서 방향을 잡기 위해 사용되었습니다.Pfund 하늘 나침반은 1950년대에 태양과 별이 보이지 않을 때(예: 낮 구름이나 황혼 아래) 지구 자기장의 극 근처를 항해할 때 사용되었다.논쟁적으로 바이킹들이 12세기에 아시아에서 유럽으로 자기 나침반이 도착하기 전인 9-11세기에 북대서양을 횡단하는 광범위한 탐험에서 이와 유사한 장치('일광석')를 이용했다는 것이 제시되었다.하늘 나침반과 관련된 것은 19세기 [35]: 67–69 말에 찰스 휘트스톤에 의해 발명된 "북극 시계"입니다.
디스플레이 테크놀로지
액정표시장치(LCD) 기술의 원리는 액정 어레이에 의한 선형 편광축의 회전에 의존합니다.백라이트로부터의 빛(또는 백라이트를 포함하지 않거나 필요로 하는 디바이스의 경우 백라이트 반사층)은 먼저 선형 편광 시트를 통과합니다.편광은 실제 액정층을 통과합니다.액정층은 픽셀 단위(TV 또는 컴퓨터 모니터용)로 구성되거나 7세그먼트 디스플레이나 특정 제품에 대한 커스텀 기호가 있는 것과 같은 다른 형식으로 구성될 수 있습니다.액정층은 기본적으로 작은 나선형으로 구성된 일관된 오른손(또는 왼손) 키랄리티로 생성됩니다.이로 인해 원형의 복굴절이 발생하며 선형 편광 상태가 90도 회전하도록 설계되어 있습니다.그러나 셀 전체에 전압이 인가되면 분자는 직진하여 원형 복굴절을 감소시키거나 완전히 상실합니다.디스플레이의 보기 측면에는 다른 선형 편광 시트가 있으며, 일반적으로 활성 레이어 뒤쪽에서 90도 방향을 잡습니다.따라서 충분한 전압을 인가하여 원형 복굴절을 제거하면 투과광의 편광은 전면 편광자와 직각으로 유지되어 화소가 어둡게 나타난다.그러나 전압이 없는 경우 편광의 90도 회전으로 인해 전면 편광자의 축과 정확히 일치하여 빛이 통과할 수 있습니다.중간전압은 편광축의 중간회전을 생성하며 화소는 중간강도를 가진다.이 원리에 근거한 디스플레이는 널리 보급되어 있으며, 현재는 텔레비전, 컴퓨터 모니터, 비디오 프로젝터의 대부분에 사용되고 있기 때문에, 이전의 CRT 테크놀로지는 거의 사용되지 않게 되어 있습니다.LCD 디스플레이의 동작에 편광의 사용은 편광 선글라스를 쓴 사람에게 즉시 나타나기 때문에 종종 디스플레이를 읽을 수 없게 됩니다.
전혀 다른 의미에서 편광 부호화는 3D 영화에 사용되는 입체 디스플레이에서 왼쪽과 오른쪽 눈에 개별 이미지를 전달하는 선도적인 방법(단독이 아님)이 되었습니다.여기에는 직교 방향 편광 필터를 갖춘 2개의 다른 프로젝터 또는 시간 다중 편광(연속 프레임의 고속 교대 편광 장치)을 갖춘 단일 프로젝터 중 하나에서 각 눈에 투영되는 개별 이미지가 포함됩니다.적절한 편광 필터가 있는 편광 3D 안경은 각 눈이 원하는 영상만 수신하도록 합니다.역사적으로 이러한 시스템은 비용이 저렴하고 분리가 잘 되었기 때문에 선형 편파 부호화를 사용했습니다.그러나 원형 편광은 두 이미지를 분리하는 것을 둔감하게 만들고, 리얼D의 시스템처럼 오늘날 3-D 영화 전시회에서 널리 사용되고 있다.이러한 이미지를 투사하려면 반사 시 투사된 빛의 편광을 유지하는 화면(예: 은색 화면)이 필요합니다. 일반 확산 흰색 투사 화면은 투사된 이미지의 편광을 유발하므로 이 응용 프로그램에는 적합하지 않습니다.
현재는 사용되지 않지만 CRT 컴퓨터 디스플레이는 유리 봉투에 반사되어 실내 조명에 의해 눈부심이 발생하고 결과적으로 콘트라스트가 저하되었습니다.이 문제를 개선하기 위해 몇 가지 반사 방지 솔루션이 사용되었습니다.한 용액은 원편광의 반사 원리를 이용했다.화면 앞에 있는 원형 편광 필터는 우측 원형 편광 실내광만 투과할 수 있다(예를 들어).(사용하는 규칙에 따라) 오른쪽 원편광은 +z 방향으로 전파하면서 전기(및 자기)계 방향이 시계 방향으로 회전합니다.반사를 할 때, 자기장은 여전히 같은 회전 방향을 가지지만, 이제 전파는 -z 방향으로 진행되어 반사파가 원편광으로 남습니다.반사 유리 앞에 우측 원형 편광 필터를 배치하면 유리에서 반사되는 불필요한 빛이 필터에 의해 차단되는 매우 편광 상태가 되어 반사 문제가 해소됩니다.이렇게 두 렌즈에 좌우 원편광을 채용한 3D 무비안경을 착용하고 거울을 보면 반사에 대한 원편광의 반전 및 반사의 제거를 쉽게 볼 수 있다.한쪽 눈을 감으면 다른 쪽 눈은 자신을 볼 수 없는 반사를 볼 수 있습니다; 그 렌즈는 검은색으로 보입니다.그러나 다른 렌즈(감긴 눈의 렌즈)는 올바른 원형 편광으로 인해 감긴 눈을 쉽게 볼 수 있습니다.
무선 송수신
송수신에 사용되는 모든 무선(및 마이크로파) 안테나는 본질적으로 편광되어 있습니다.특정 편광을 송신(또는 수신)하여 반대편광에 전혀 민감하지 않습니다.특정 편광은 방향의 함수입니다.대부분의 안테나는 명목상 직선편광이지만 타원편광과 원형편광의 가능성이 있습니다.광학의 관례와 마찬가지로 전파의 '편파'는 직선의 편파에 대해 자기장이 90도 회전하는 것을 전계의 편파라고 한다.
대부분의 안테나는 직선 편광입니다.실제로 대칭성을 고려했을 때 관측자를 포함한 평면 내에 있는 안테나는 그 평면 방향으로만 편파를 가질 수 있다는 것을 알 수 있습니다.이는 많은 경우에 적용되므로 의도된 전파 방향에서 그러한 안테나의 편파를 쉽게 추론할 수 있다.두 번째 스테이션에서 수평을 향해 볼 때 전형적인 옥상 야기 또는 수평 도체를 가진 로그 주기 안테나는 반드시 수평 편광입니다.그러나 안테나 소자로 사용되는 수직 "wip antenna" 또는 AM 방송 타워는 수직 편광으로 송신됩니다.4개의 암이 수평면에 있는 턴스타일 안테나는 마찬가지로 수평 편파 방사선을 수평 방향으로 송신합니다.그러나 동일한 턴스타일 안테나를 "축 모드"(상향적으로 동일한 수평 방향 구조)로 사용하면 방사선이 원형으로 편광됩니다.중간 고도에서는 타원 편광입니다.
예를 들어 수평 편파 안테나를 사용하여 수직 편파 송신을 수신하려고 하면 신호 강도가 상당히 감소하기 때문에 편파는 무선 통신에서 중요합니다.이 원리는 고정 주파수 대역에서 채널 용량을 두 배로 늘리기 위해 위성 TV에서 사용됩니다.동일한 주파수 채널을 반대편광으로 브로드캐스트되는 두 신호에 사용할 수 있습니다.수신 안테나를 한쪽 편파용으로 조정함으로써 어느 한쪽의 신호를 다른 한쪽의 간섭 없이 선택할 수 있다.
특히 지면의 존재로 인해 수평 편광과 수직 편광 사이에 전파(및 TV 고스트의 원인이 되는 반사)에 약간의 차이가 있다.AM과 FM 방송 라디오는 보통 수직 편파를 사용하고 텔레비전은 수평 편파를 사용합니다.특히 저주파에서는 수평편파를 회피한다.그것은 수평 편파의 위상이 지면에 반사될 때 역전되기 때문이다.수평 방향의 먼 스테이션은 직접파와 반사파를 모두 수신하므로 서로 상쇄되는 경향이 있습니다.이 문제는 수직 편파에서는 회피됩니다.편광은 레이더 펄스의 송신과 동일 또는 다른 안테나의 레이더 반사 수신에서도 중요합니다.예를 들면, 원편파를 이용하는 것으로, 빗방울에 의한 레이더 펄스의 후방 산란을 회피할 수 있다.위에서 설명한 것처럼 원편광의 반사반사가 편광의 핸드니스(handshness)를 반전시키듯이, 빗방울과 같은 파장보다 훨씬 작은 물체에 의한 산란에도 같은 원리가 적용된다.반면에, 불규칙한 금속 물체 (비행기 등)에 의한 파동의 반사는 일반적으로 편광의 변화와 동일한 안테나에 의한 (부분적인) 귀환파의 수신을 야기합니다.
지구 자기장과 함께 전리층에서의 자유 전자의 효과는 일종의 원형 복굴절인 패러데이 회전을 일으킨다.이는 아래와 같이 성간 공간에서 전자에 의해 선형 편광의 축을 회전시킬 수 있는 메커니즘과 같다.이러한 플라즈마에 의한 패러데이 회전의 크기는 저주파에서는 크게 과장되기 때문에 위성이 사용하는 마이크로파 주파수가 높을 경우 그 영향은 미미하다.그러나 전리층에 의한 굴절 후에 수신되는 중파 또는 단파 전송은 강한 영향을 받는다.전리층을 통과하는 파의 경로와 이러한 경로를 따라 흐르는 지구의 자기장 벡터는 예측할 수 없기 때문에, 수직(또는 수평) 편광으로 전송되는 파는 일반적으로 수신기에서 임의 방향으로 편광을 발생시킵니다.
양극화와 비전
많은 동물들은 빛의 편광의 일부 구성 요소(예: 선형 수평 편광)를 지각할 수 있다.하늘 빛의 선형 편광은 항상 태양의 방향과 수직이기 때문에 일반적으로 항법 목적으로 사용됩니다.이 능력은 벌들을 포함한 곤충들 사이에서 매우 흔하며,[35]: 102–103 그들은 그들의 의사소통 춤의 방향을 잡기 위해 이 정보를 사용합니다.낙지, 오징어, 오징어, 갑오징어,[35]: 111–112 갯가제비 등에서도 분극 감수성이 관찰됐다.후자의 경우, 한 종은 편광의 직교 성분 6개를 모두 측정하며,[36] 최적의 편광 시야를 가진 것으로 여겨진다.의사소통에 사용되는 갑오징어의 피부 패턴이 빠르게 변화하고 선명하게 색칠된 것도 편광 패턴을 포함하고 있으며, 갯가제비도 편광 선택 반사 조직을 가지고 있는 것으로 알려져 있다.하늘 편광은 비둘기에 의해 인식되는 것으로 생각되었고, 비둘기는 귀소작용에 도움을 주는 것으로 추정되었지만, 연구는 이것이 일반적인 [37]신화라고 밝히고 있다.
인간의 육안에서는 필터가 필요 없이 편광에 약하게 민감합니다.편광은 하이딩거 브러시라고 불리는 시야의 중심 부근에 매우 희미한 패턴을 만듭니다.이 패턴은 매우 보기 어렵지만, 연습하면 편광을 육안으로 [35]: 118 감지하는 것을 배울 수 있다.
원형 편광을 이용한 각운동량
전자기 복사는 전파 방향으로 일정한 선형 운동량을 운반하는 것으로 잘 알려져 있다.그러나 또한 빛이 원형으로 편광되어 있으면(또는 부분적으로 편광되어 있으면) 일정한 각운동량을 운반합니다.마이크로파 등 낮은 주파수에 비해 빛의 각운동량은 같은 파형의 선형운동량(또는 방사압)에 비해 순수 원형편파라도 매우 작으며 측정조차 어렵다.그러나 분당 [38][39]최대 6억 회전의 속도를 달성하기 위한 실험에 이용되었다.
「 」를 참조해 주세요.
레퍼런스
인용된 레퍼런스
- ^ Shipman, James; Wilson, Jerry D.; Higgins, Charles A. (2015). An Introduction to Physical Science, 14th Ed. Cengage Learning. p. 187. ISBN 978-1-305-54467-3.
- ^ Muncaster, Roger (1993). A-level Physics. Nelson Thornes. pp. 465–467. ISBN 0-7487-1584-3.
- ^ Singh, Devraj (2015). Fundamentals of Optics, 2nd Ed. PHI Learning Pvt. Ltd. p. 453. ISBN 978-8120351462.
- ^ a b Avadhanulu, M. N. (1992). A Textbook of Engineering Physics. S. Chand Publishing. pp. 198–199. ISBN 8121908175.
- ^ Desmarais, Louis (1997). Applied Electro Optics. Pearson Education. pp. 162–163. ISBN 0-13-244182-9.
- ^ Le Tiec, A.; Novak, J. (July 2016). "Theory of Gravitational Waves". An Overview of Gravitational Waves. pp. 1–41. arXiv:1607.04202. doi:10.1142/9789813141766_0001. ISBN 978-981-314-175-9. S2CID 119283594.
- ^ Lipson, Stephen G.; Lipson, Henry; Tannhauser, David Stefan (1995). Optical Physics. Cambridge University Press. pp. 125–127. ISBN 978-0-521-43631-1.
- ^ a b Waldman, Gary (2002). Introduction to Light: The Physics of Light, Vision, and Color. Courier Corporation. pp. 79–80. ISBN 978-0-486-42118-6.
- ^ Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X.
- ^ Geoffrey New (7 April 2011). Introduction to Nonlinear Optics. Cambridge University Press. ISBN 978-1-139-50076-0.
- ^ Dorn, R.; Quabis, S. & Leuchs, G. (Dec 2003). "Sharper Focus for a Radially Polarized Light Beam". Physical Review Letters. 91 (23): 233901. Bibcode:2003PhRvL..91w3901D. doi:10.1103/PhysRevLett.91.233901. PMID 14683185.
- ^ Chandrasekhar, Subrahmanyan (1960). Radiative Transfer. Dover. p. 27. ISBN 0-486-60590-6. OCLC 924844798.
- ^ a b Sletten, Mark A.; Mc Laughlin, David J. (2005-04-15). "Radar Polarimetry". In Chang, Kai (ed.). Encyclopedia of RF and Microwave Engineering. John Wiley & Sons, Inc. doi:10.1002/0471654507.eme343. ISBN 978-0-471-65450-6.
- ^ Schrank, Helmut E.; Evans, Gary E.; Davis, Daniel (1990). "6 Reflector Antennas" (PDF). In Skolnik, Merrill Ivan (ed.). Radar Handbook (PDF). McGraw-Hill. pp. 6.30, Fig 6.25. ISBN 978-0-07-057913-2.
- ^ Ishii, T. Koryu, ed. (1995). Handbook of Microwave Technology. Vol. 2: Applications. Elsevier. p. 177. ISBN 978-0-08-053410-7.
- ^ Volakis, John (2007). Antenna Engineering Handbook, Fourth Edition. McGraw-Hill. Sec. 26.1. ISBN 9780071475747: Note: in contrast with other authors, this source initially defines ellipticity reciprocally, as the minor-to-major-axis ratio, but then goes on to say that "Although [it] is less than unity, when expressing ellipticity in decibels, the minus sign is frequently omitted for convenience", which essentially reverts to the definition adopted by other authors.
{{cite book}}: CS1 유지보수: 포스트스크립트(링크) - ^ Prakash, Hari; Chandra, Naresh (1971). "Density Operator of Unpolarized Radiation". Physical Review A. 4 (2): 796–799. Bibcode:1971PhRvA...4..796P. doi:10.1103/PhysRevA.4.796.
- ^ Chandrasekhar, Subrahmanyan (2013). Radiative transfer. Courier. p. 30.
- ^ a b c d e f Hecht, Eugene (2002). Optics (4th ed.). United States of America: Addison Wesley. ISBN 0-8053-8566-5.
- ^ Edward L. O'Neill (January 2004). Introduction to Statistical Optics. Courier Dover Publications. ISBN 978-0-486-43578-7.
- ^ Eismann, J. S.; Nicholls, L. H.; Roth, D. J.; Alonso, M. A.; Banzer, P.; Rodríguez-Fortuño, F. J.; Zayats, A. V.; Nori, F.; Bliokh, K. Y. (2021). "Transverse spinning of unpolarized light". Nature Photonics. 15 (2): 156–161. arXiv:2004.02970. Bibcode:2021NaPho..15..156E. doi:10.1038/s41566-020-00733-3. ISSN 1749-4885. S2CID 215238513.
- ^ Sugic, Danica; Dennis, Mark R.; Nori, Franco; Bliokh, Konstantin Y. (2020-12-23). "Knotted polarizations and spin in three-dimensional polychromatic waves". Physical Review Research. 2 (4): 042045. arXiv:2007.13307. Bibcode:2020PhRvR...2d2045S. doi:10.1103/PhysRevResearch.2.042045. ISSN 2643-1564.
- ^ Dennis Goldstein; Dennis H. Goldstein (3 January 2011). Polarized Light, Revised and Expanded. CRC Press. ISBN 978-0-203-91158-7.
- ^ Masud Mansuripur (2009). Classical Optics and Its Applications. Cambridge University Press. ISBN 978-0-521-88169-2.
- ^ Randy O. Wayne (16 December 2013). Light and Video Microscopy. Academic Press. ISBN 978-0-12-411536-1.
- ^ Peter M. Shearer (2009). Introduction to Seismology. Cambridge University Press. ISBN 978-0-521-88210-1.
- ^ Seth Stein; Michael Wysession (1 April 2009). An Introduction to Seismology, Earthquakes, and Earth Structure. John Wiley & Sons. ISBN 978-1-4443-1131-0.
- ^ Vollhardt, K. Peter C.; Schore, Neil E. (2003). Organic Chemistry: Structure and Function (4th ed.). W. H. Freeman. pp. 169–172. ISBN 978-0-7167-4374-3.
- ^ Vlemmings, W. H. T. (Mar 2007). "A review of maser polarization and magnetic fields". Proceedings of the International Astronomical Union. 3 (S242): 37–46. arXiv:0705.0885. Bibcode:2007IAUS..242...37V. doi:10.1017/s1743921307012549.
- ^ Hannu Karttunen; Pekka Kröger; Heikki Oja (27 June 2007). Fundamental Astronomy. Springer. ISBN 978-3-540-34143-7.
- ^ Boyle, Latham A.; Steinhardt, PJ; Turok, N (2006). "Inflationary predictions for scalar and tensor fluctuations reconsidered". Physical Review Letters. 96 (11): 111301. arXiv:astro-ph/0507455. Bibcode:2006PhRvL..96k1301B. doi:10.1103/PhysRevLett.96.111301. PMID 16605810. S2CID 10424288.
- ^ Tegmark, Max (2005). "What does inflation really predict?". Journal of Cosmology and Astroparticle Physics. 0504 (4): 001. arXiv:astro-ph/0410281. Bibcode:2005JCAP...04..001T. doi:10.1088/1475-7516/2005/04/001. S2CID 17250080.
- ^ Clark, S. (1999). "Polarised starlight and the handedness of Life". American Scientist. 97 (4): 336–43. Bibcode:1999AmSci..87..336C. doi:10.1511/1999.4.336.
- ^ Bekefi, George; Barrett, Alan (1977). Electromagnetic Vibrations, Waves, and Radiation. USA: MIT Press. ISBN 0-262-52047-8.
- ^ a b c d J. David Pye (13 February 2001). Polarised Light in Science and Nature. CRC Press. ISBN 978-0-7503-0673-7.
- ^ Sonja Kleinlogel; Andrew White (2008). "The secret world of shrimps: polarisation vision at its best". PLOS ONE. 3 (5): e2190. arXiv:0804.2162. Bibcode:2008PLoSO...3.2190K. doi:10.1371/journal.pone.0002190. PMC 2377063. PMID 18478095.
- ^ Nuboer, J. F. W.; Coemans, M. a. J. M.; Vos Hzn, J. J. (1995-02-01). "No evidence for polarization sensitivity in the pigeon electroretinogram". Journal of Experimental Biology. 198 (2): 325–335. doi:10.1242/jeb.198.2.325. ISSN 0022-0949. PMID 9317897.
- ^ "'Fastest spinning object' created". BBC News. 2013-08-28. Retrieved 2019-08-27.
- ^ Dholakia, Kishan; Mazilu, Michael; Arita, Yoshihiko (August 28, 2013). "Laser-induced rotation and cooling of a trapped microgyroscope in vacuum". Nature Communications. 4: 2374. Bibcode:2013NatCo...4.2374A. doi:10.1038/ncomms3374. hdl:10023/4019. PMC 3763500. PMID 23982323.
일반 참고 자료
- 광학의 원리, 제7판, M. Born & E. Wolf, 캠브리지 대학, 1999, ISBN 0-521-64222-1.
- 편광의 기초: 통계 광학 접근법, C. Broseau, Wiley, 1998, ISBN 0-471-14302-2.
- Polarite Light, 제2판, Dennis Goldstein, Marcel Dekker, 2003, ISBN 0-8247-4053-X.
- 편광 필드 가이드, 에드워드 콜렛, SPIE 필드 가이드 vol.FG05, SPIE, 2005, ISBN 0-8194-5868-6.
- 전기통신 편광광학, Jay N. Damask, Springer 2004, ISBN 0-387-22493-9.
- 자연 편광, G. P. 쾨넨, 1985년 캠브리지 대학, G. A. 비어링 지음, ISBN 0-521-25862-6.
- 과학과 자연의 편광, D. Pye, 물리연구소, 2001, ISBN 0-7503-0673-4.
- 편광, 생산 및 사용, 윌리엄 A.1962년 하버드 대학교 슈클리프
- Ellipsometry and 편광, R. M. A. Azzam and N. M. Bashara, North-Holland, 1977, ISBN 0-444-87016-4.
- 바이킹 항해자들의 비밀-바이킹들이 어떻게 그들의 놀라운 일광석과 다른 기술들을 외양을 건너기 위해 사용했는지, Leif Karlson, One Earth Press, 2003.
외부 링크
- 분극에 관한 파인만의 강의
- 자연과 테크놀로지의 편광
- 편광광 디지털 이미지 갤러리: 편광 효과를 이용한 현미경 이미지 작성
- 콜로라도대 물리학과 2000의 편광: 편광에 대한 애니메이션 설명
- 산술 페이지:광자 스핀과 편광의 관계
- 가상 편광 현미경
- 위성 안테나의 편광 각도.
- 사진에 편광자 사용
- 분자 표현: 과학, 광학, 그리고 당신 - 빛의 편광:대화형 Java 튜토리얼
- 분극에 관한 SPIE 기술 그룹
- 안테나 편파
- YouTube의 선형, 원형, 타원 편광 애니메이션













 평방미터당 약 .
평방미터당 약 .





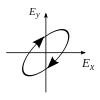




 2
2 전계 벡터의 2개 성분에서 파형의 진폭을 나타내고
전계 벡터의 2개 성분에서 파형의 진폭을 나타내고 
 위상을 나타냅니다.
위상을 나타냅니다.














 단일 파워(
단일 파워(