횡파

단순한 광파에서 광선을 따라 전기장(빨간색)과 자기장(파란색)을 설명합니다.광선에 수직인 평면의 경우 각 필드는 평면의 모든 점에서 항상 동일한 값을 가집니다.

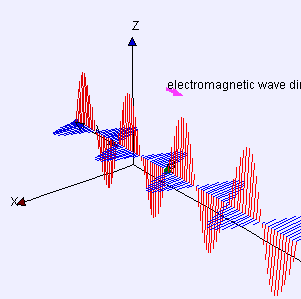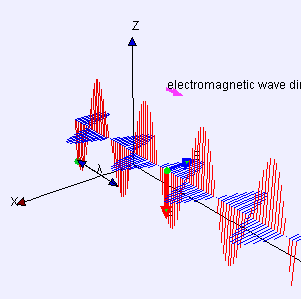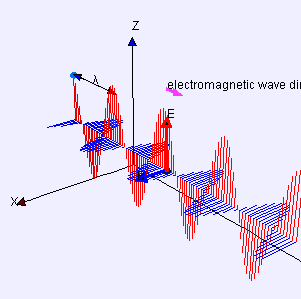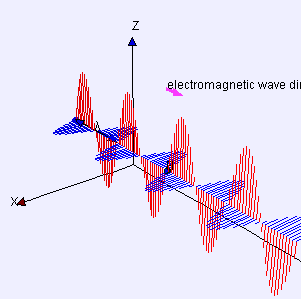
물리학에서 횡파(verse波, )는 파동의 진행 방향에 수직으로 진동하는 파동을 말합니다.반대로 종파는 진동 방향으로 진행합니다.

한 쪽 끝을 고정하고 다른 쪽 끝을 상하로 이동시켜 줄 가로 길이의 줄 위에 만들 수 있는 파도가 간단한 예입니다.또 다른 예는 드럼의 막에 만들어지는 파도입니다.파동은 막 면에 평행한 방향으로 전파되지만, 막 자체의 각 점은 그 면에 수직으로 상하로 이동합니다.빛은 횡파의 또 다른 예로, 진동은 전파의 방향을 설명하는 이상적인 광선에 직각으로 가리키는 전기장과 자기장입니다.

횡파는 일반적으로 발생하는 전단 응력으로 인해 탄성 고체에서 발생합니다. 이 경우의 진동은 고체 입자가 완화된 위치에서 벗어나 파동의 전파에 수직인 방향으로 이동하는 것입니다.이러한 변위는 재료의 국부적인 전단 변형에 해당합니다.따라서 이러한 성질의 횡파를 전단파라고 합니다.유체는 정지 상태에서는 전단력에 저항할 수 없기 때문에 유체 내부에서 횡파의 전파는 ^[1]불가능합니다.지진학에서 전단파는 2차파 또는 S파라고도 불립니다.

횡파는 종파와 대비되며, 여기서 진동은 파동 방향으로 발생합니다.종파의 표준적인 예는 기체, 액체 또는 고체의 음파 또는 "압력파"이며, 진동은 파동이 전파하는 물질의 압축과 팽창을 야기합니다.압력파는 지구물리학에서 "1차 파동" 또는 "P파"라고 불립니다.

파도는 종방향 ^[2]운동과 횡방향 운동을 모두 포함합니다.

수학 공식화

수학적으로, 가장 간단한 종류의 횡파는 평면 선형 편광 정현파입니다.여기서 "평면"은 전파 방향이 매체 전체에서 변하지 않고 같다는 것을 의미합니다. "선형 편광"은 변위 방향도 매체 전체에서 변하지 않고 같다는 것을 의미합니다. 그리고 변위의 크기는 전파 방향을 따라 시간과 위치에 대해서만 정현 함수입니다.

이러한 파동의 운동은 수학적으로 다음과 같이 표현될 수 있습니다.d를 전파 방향(단위 길이를 갖는 벡터)이라 하고, 매질 내의 임의의 기준점이라 합니다.진동(d에 수직인 또 다른 단위 길이 벡터)의 방향이라고 가정합니다.매질의 임의의 점 p 및 임의의 시간 t(초)에서의 입자의 변위는

S(p,t)=Au\sin \left({\frac {t-(p-o)){\frac {d}{v}}{{T}}+\phi \right)

여기서 A는 파동의 진폭 또는 세기, T는 주기, v는 전파 속도, δ는 위상 ato입니다.이 모든 매개 변수는 실수입니다.기호 "•"는 두 벡터의 내적을 나타냅니다.

이 방정식에 의해 파동은 d 방향으로 진행하고 진동은 u 방향을 따라 앞뒤로 발생합니다.파동은 u 방향으로 선편광되어 있다고 합니다.

고정된 점 p를 관찰하는 관찰자는 각 의미에서 최대 입자 변위 A를 갖는, 즉 매초마다 f = 1/T의 완전한 진동 주기를 갖는, 주기 T 초를 갖는 단순한 고조파(정형) 운동으로 입자가 움직이는 것을 볼 것입니다.고정된 시간 t에서 모든 입자의 스냅샷은 d에 수직인 각 평면의 모든 입자에 대해 동일한 변위를 보여줄 것이며, 연속적인 평면의 변위는 정현파 패턴을 형성하고, 각 전체 주기는 파장 λ = v T = v/f에 따라 연장됩니다.전체 패턴은 속도 V에 따라 d 방향으로 이동합니다.

동일한 방정식은 "변위" S(p, t)가 p 시점과 t 시점의 전기장이라는 것을 제외하고는 평면 편광 정현파를 설명합니다. (자기장은 동일한 방정식으로 설명되지만 d와 u 모두에 수직이고 진폭이 다른 "변위" 방향으로 설명됩니다.)

중첩원리

균일한 선형 매질에서 복잡한 진동(물질의 진동 또는 빛의 흐름)은 가로 또는 세로의 많은 단순한 정현파의 중첩으로 설명될 수 있습니다.

예를 들어 바이올린 현의 진동은 현을 위나 아래 또는 왼쪽에서 오른쪽으로 이동시키는 다양한 주파수의 많은 횡파의 합으로 분석될 수 있습니다.연못의 잔물결은 함께 전파되는 횡파와 종파(중력파)의 조합으로 분석될 수 있습니다.

원형편광

매질이 선형이고 동일한 이동 방향 d에 대해 여러 개의 독립적인 변위 방향을 허용하는 경우, 우리는 편광의 두 개의 상호 수직 방향을 선택할 수 있고, 다른 방향으로 선형 편광된 모든 파동을 그 두 파동의 선형 조합(혼합)으로 표현할 수 있습니다.

진동수, 속도, 진행 방향은 같으나 위상과 독립적인 변위 방향이 다른 두 파동을 결합함으로써 원형 또는 타원형의 편광파를 얻을 수 있습니다.이러한 파동에서 입자는 앞뒤로 움직이는 대신 원형이나 타원형의 궤적을 묘사합니다.

위에서 언급한 팽팽한 끈으로 사고 실험을 다시 하는 것이 이해에 도움이 될 수 있습니다.손을 위아래가 아닌 오른쪽과 왼쪽으로 움직여 줄에 파도를 일으킬 수도 있습니다.이것은 중요한 점입니다.파동이 움직일 수 있는 두 개의 독립적인 (직교적인) 방향이 있습니다. (이것은 직각의 임의의 두 방향에 대해서도 적용되며, 명확성을 위해 상하좌우로 선택됩니다.)손을 직선으로 움직여 발사되는 모든 파동은 선편파입니다.

하지만 이제 여러분의 손이 원을 그리며 움직인다고 상상해 보세요.움직임에 따라 문자열에 나선형 물결이 일게 됩니다.손을 상하 좌우로 동시에 움직이고 있습니다.좌우 운동의 최대치는 상하 운동의 최대치로부터 1/4 파장(또는 원 둘레의 1/4, 즉 90도 또는 λ/2 라디안)이 발생합니다.끈을 따라 어느 지점에서나 끈의 변위는 손과 같은 원을 설명하지만 파동의 전파 속도에 의해 지연됩니다.또한 손을 시계 방향으로 원을 그리거나 반시계 방향으로 원을 그리도록 선택할 수 있습니다.이러한 교대 원운동은 오른쪽과 왼쪽 원편파를 생성합니다.

당신의 원이 불완전한 정도까지, 규칙적인 움직임은 타원을 설명하고 타원 편광을 만듭니다.편심의 극치에서는 타원이 직선이 되어 타원의 장축을 따라 선형 편광을 만듭니다.타원 운동은 항상 진폭이 같지 않고 위상이 90도인 두 직교 선형 운동으로 분해될 수 있으며, 원형 편광은 두 선형 운동이 동일한 진폭을 갖는 특별한 경우입니다.

고무실에 기계적으로 생성된 원형편광은 기계적 편광 필터에 의해 선형편광으로 변환됩니다.

횡파의 힘 문자열

(끈의 선형 질량 밀도를 μ라고 합니다.)

횡파에서 질량을 가진 원소의 운동 에너지는 다음과 같습니다.

dK={\frac {1}{2}}\dm\v_{y}^{2}={\frac {1}{2}}\mux\A^{2}\omega ^{2}\cos ^{2}\left ({\frac {2\pix}{\mux}}-\omega t\right)

한 파장에서 운동에너지

K={\frac {1}{2}}\mu A^{2}\omega ^{2}\int_{0}^{\lot }\cos ^{2}\left ({\frac {2\pix}{\lot }-\omega t\right)dx={\frac {1}{4}\mu A^{2}\omega ^{2}\lot

후크의 법칙을 이용한 질량요소에서의 퍼텐셜에너지

dU={\frac {1}{2}}\dm\omega ^{2}={\frac {1}{2}}\dx\omega ^{2}\sin ^{2}\left ({\frac {2\pix}{\displaystyle dU{{}-\omega t\right)

그리고 하나의 파장에 대한 퍼텐셜 에너지.

U={\frac {1}{2}}\mu A^{2}\omega ^{2}\int_{0}^{\lot }\sin ^{2}\left ({\frac {2\pix}{\lot }-\omega t\right)dx={\frac {1}{4}\mu A^{2}\omega ^{2}\lot

따라서, 한 파장 ${\textstyle K+U={\frac {1}{2}}\mu A^{2}\omega ^{2}\lambda }$ + ${\textstyle K+U={\frac {1}{2}}\mu A^{2}\omega ^{2}\lambda }$ = ${\textstyle K+U={\frac {1}{2}}\mu A^{2}\omega ^{2}\lambda }$ 2 ${\textstyle K+U={\frac {1}{2}}\mu A^{2}\omega ^{2}\lambda }$ ${\textstyle K+U={\frac {1}{2}}\mu A^{2}\omega ^{2}\lambda }$ 2 ω 2 λ ${\textstyle$ K $+U$ = {\ $frac {1}{2}}\mu$ A $^{2}\omega ^{2}\$ mu $}$

따라서 평균 전력은 ${\textstyle {\frac {1}{2}}\mu A^{2}\omega ^{2}v_{x}}$ 2 ≥ ${\textstyle {\frac {1}{2}}\mu A^{2}\omega ^{2}v_{x}}$ ${\$ {\ $frac {1}{2}}\mu$ A $^{2}\omega$ ^{ $2}v_{x$ }}입니다.

참고 항목

종파
광파의 가정된 매개체인 루미네랄 에테르는 빛이 횡파라는 것을 받아들이면서 이 물리적 매개체의 증거를 찾게 되었습니다.
전단파 분열
전자기파 방정식의 정현 평면파 해
가로모드
엘라스토그래피
전단파 탄성영상

참고문헌

^ "Fluid Mechanics II: Viscosity and Shear stresses" (PDF).{{cite web}}: CS1 유지 : url-status (링크)
^ {[사이트웹 제목=종횡파동 url=https://www.acs.psu.edu/drussell/demos/waves/wavemotion.html }}
^ "16.4 Energy and Power of a Wave - University Physics Volume 1 OpenStax". openstax.org. Retrieved 2022-01-28.

외부 링크

횡파 상호작용 시뮬레이션
초고속 필름 및 애니메이션으로 설명되는 웨이브 유형
Weisstein, Eric Wolfgang (ed.). "Transverse Wave". ScienceWorld.
Connexion에서 횡파 및 종파의 이러한 파에 대한 입문 모듈

[1] "Fluid Mechanics II: Viscosity and Shear stresses" (PDF).{{cite web}}: CS1 유지 : url-status (링크)

[2] {[사이트웹 제목=종횡파동 url=https://www.acs.psu.edu/drussell/demos/waves/wavemotion.html }}

[3] "16.4 Energy and Power of a Wave - University Physics Volume 1 OpenStax". openstax.org. Retrieved 2022-01-28.

[1]

[2]

v t 현악기, 전선, 악기
목록 (혼보스텔–삭스 번호)
절하다 다리 제3교 코드폰 코스 드론 인하모닉 핑거보드 프렛 기본/하모닉스/오버톤/스트링 고조파 종파 장현악기 멜데의 실험 메르센의 법칙 모노코드 길고 가는 전선에서 음악을 연주합니다. 마디 견과 재진입 축척길이 사운드보드 정재파 끈진동 횡파 튜닝 페그
모노코드와 절, 절	아하딘 베림바우 블래더 피들 붐바 단보우 디들리 활 두시안킨 엑타라 그라운드 활 이치겐킨 일본의 바이올린 죠하프 징공 고고나 호무즈 쿠빙 모싱 먹꾸리 랑겔릭 레시바 마센코 오나빌루 살모디콘 트롬바 마리나 툼비 우무두리 유니타르 세면기저귀

Search

횡파

네임스페이스

더

목차