원형 양극화

전자동학에서 전자파의 원형 양극화는 각 지점에서 파장의 전자기장이 일정한 크기를 가지며 파동의 방향에 수직인 평면에서 일정한 속도로 회전하는 양극화 상태를 말한다.

전기역학에서 전기장의 강도와 방향은 전기장 벡터에 의해 정의된다. 동봉된 애니메이션에서 보듯이 원형 편극 파형의 경우, 우주에서 주어진 지점에서 전기장 벡터의 끝은 시간과 공간을 통해 이동하면서 빛의 위상과 관련된다. 언제라도 파동의 전기장 벡터는 전파 방향을 따라 방향의 나선형의 점을 나타낸다. 원형 편극 파형은 전파 방향과 관련하여 전기장 벡터가 우측으로 회전하는 시계 방향 또는 우측 원형 편극(RHCP)과 벡터가 좌측 감응으로 회전하는 시계 반대 방향 또는 좌측 방향 원형 편극(LHCP)의 두 가지 감각 중 하나로 회전할 수 있다.e

원형 양극화는 타원형 양극화의 제한적인 경우다. 또 다른 특별한 경우는 이해하기 쉬운 선형 양극화다.

양극화 현상은 빛이 2차원 횡파로 작용한 결과 발생한다.

원형 양극화는 두 직교 전기장 구성 요소 벡터가 크기가 동일하고 정확히 90° 또는 1/4 파장만큼 위상을 벗어날 때 발생한다.

일반 설명

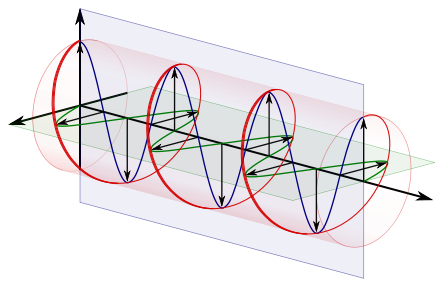
오른쪽에는 원형 극성 전자파의 전기장 벡터가 그려져 있다.^[1] 각각의 전기장 벡터 및 이들의 결합 벡터는 일정한 크기를 가지며 위상 각도가 변화한다. 이것이 평면파라는 점에서 각 벡터는 광축에 수직인 전체 평면에 대한 전기장의 크기와 방향을 나타낸다. 구체적으로는 이것이 원형 편극 평면파임을 감안하여, 이 벡터들은 평면에서 평면으로의 전기장이 일정한 강도를 가지는 동시에 방향이 일정하게 회전한다는 것을 나타낸다. 이 동적 특성을 더 잘 이해하려면 평면 파형 기사의 이 두 이미지를^{[dead link]} 참조하십시오. 이 빛은 수신기가 볼 때 우측, 시계방향으로 원형으로 편광된 것으로 간주된다. 이것은 전자기파이기 때문에 각 전기장 벡터는 전기장 벡터에 직각이며 그에 비례하는 자기장 벡터를 가지고 있지만, 설명되지는 않는다. 결과적으로, 자기장 벡터는 표시되면 두 번째 나선형을 추적할 것이다.

원형의 양극화는 광학 분야에서 흔히 접하게 되며, 이 절에서는 전자파를 단순히 빛이라고 칭하게 될 것이다.

원형 양극화의 성격과 다른 양극화와의 관계는 흔히 전기장이 서로 수직인 두 가지 요소로 나뉘어져 있다고 생각함으로써 이해된다. 수직 구성 요소와 해당 평면은 파란색으로, 수평 구성 요소와 해당 평면은 녹색으로 표시한다. 우측(이동 방향에 상대적인) 수평 구성 요소는 90° 위상 차이인 파장의 1/4만큼 수직 구성 요소를 리드한다는 점에 유의하십시오. 나선을 만들고 수직 성분의 최대 크기 지점이 수평 성분의 0 크기 지점과 일치하도록 하는 것은 이 4차 위상 관계이며, 그 반대의 경우도 마찬가지다. 이 정렬의 결과는 나선에 해당하는 선택 벡터로서 수직 및 수평 구성 요소의 최대값과 정확히 일치한다.

이 4차 위상 편이 일정한 크기를 유지하면서 회전하는 전기장에 어떻게 대응하는지 알아보려면 점 하나가 원을 그리며 시계 방향으로 이동한다고 상상해 보십시오. 원의 중심에 상대적인 점의 수직적 및 수평적 변위가 시간에 따라 정현상적으로 변화하고 주기의 1/4만큼 위상으로부터 벗어나는 방법을 생각해 보십시오. 수직 최대 변위에 도달하기 전에 수평 최대 변위(왼쪽 아래)가 사이클의 1/4에 도달하기 때문에 변위는 사이클의 1/4 위상에서 벗어난다고 한다. 이제 그림을 다시 언급하면서 앞에서 뒤로 축을 따라 이동하면서 방금 설명한 원의 중심을 상상해 보십시오. 빙글빙글 도는 점은 수직 변위를 이끄는 좌향의 나선형을 추적할 것이다. 회전하는 점의 수평 및 수직 변위가 시간상 주기 1/4만큼 위상에서 벗어나듯이, 전기장의 수평 및 수직 구성 요소의 크기는 파장의 1/4만큼 위상에서 벗어난다.

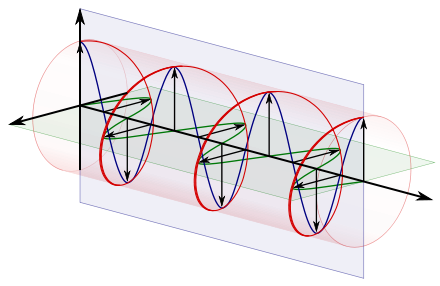
다음 한 쌍의 그림은 수신기가 볼 때 왼손잡이, 시계 반대 방향으로 원형으로 편광된 광선이다. 왼손잡이기 때문에, 우향(이동 방향과 상대적) 수평 구성요소는 이제 수직 구성요소를 리드하기보다는 파장의 1/4만큼 뒤처지고 있다.

핸드니스의 반전

웨이브플레이트

원형으로 편광된 빛을 다른 손으로 변환하기 위해서는 반파판을 사용할 수 있다. 반파판은 빛의 주어진 선형 구성요소를 직교 선형 구성요소에 비례하여 파장의 1/2로 이동시킨다.

반사

편광의 손길은 정상 발생 시 표면에서 반사된다. 그러한 반사에 의해 반사광의 양극화 평면의 회전은 입사장의 회전과 동일하다. 그러나 이제 전파가 반대 방향으로 진행되면서, 입사 빔에 대해 "오른손"으로 설명될 수 있는 동일한 회전 방향은 역방향으로 전파를 위해 "왼손"이 되며, 그 반대의 경우도 마찬가지다. 손의 반전을 제외하고도 양극화의 타원성도 보존된다(이층 표면이 반사하는 경우는 제외).

이 원리는 정상 발생 시 반사되는 빛에 대해서만 엄격하게 유지된다는 점에 유의하십시오. 예를 들어, 방목 발생 시 유전체 표면에서 반사되는 우측 원형 편광(Brewster 각도를 벗어난 각도)은 여전히 오른손이지만 타원형 편광으로 나타날 것이다. 비정상 발생 시 금속으로 반사되는 빛은 일반적으로 타원성도 변화한다. 그러한 상황은 일반적으로 p와 s로 표시되는 입사 평면에 평행하고 수직인 선형 양극화의 구성요소로 입사 원(또는 기타) 양극화를 분해하여 해결할 수 있다. p와 s 선형 편광의 반사 성분은 반사 프레스넬 계수를 적용하여 발견되는데, 이 두 선형 편광에 대해 일반적으로 다르다. p와 s의 구분이 없는 특수한 정상 발생의 경우에만 두 성분에 대한 프레스넬 계수가 동일하여 위의 성질을 유도한다.

선형 양극화 전환

원형 편광은 4차 파형을 통과하면 선형 편광으로 변환할 수 있다. 양극화 축에 45°의 축을 두고 사분파선을 통해 선형 편광광을 통과시키면 원형 편광으로 전환된다. 사실 이것이 실제로 순환 양극화를 만드는 가장 일반적인 방법이다. 선형 편광 광선을 45°가 아닌 각도로 4분의 1 파형을 통과하면 일반적으로 타원 편광 현상이 발생한다는 점에 유의한다.

핸드메인스

원형 양극화는 전기장 벡터가 회전하는 방향에 따라 오른손 또는 왼손, 시계 방향 또는 시계 반대 방향이라고 할 수 있다. 불행히도, 두 개의 반대되는 역사적 관습이 존재한다.

출처의 관점에서 보면

이 관례를 이용하여, 양극화는 근원의 관점에서 정의된다. 이 관례를 사용할 때, 왼손 또는 오른손 엄지를 원천으로부터 멀리 가리키고, 파동이 전파하는 방향과 같은 방향으로 손가락의 컬링을 공간의 주어진 지점에서 필드의 시간적 회전 방향에 맞추어 왼손 또는 오른손 엄지를 결정한다. 파동이 시계방향으로 또는 반시계방향으로 원형으로 편광되어 있는지를 판단할 때, 다시 한 번 소스의 관점을 취하며, 소스에서 멀리 파장의 전파 방향과 같은 방향으로 바라보면서, 필드의 공간 회전의 방향을 관찰한다.

Using this convention, the electric field vector of a right-handed circularly polarized wave is as follows: ${\displaystyle \left(E_{x},\,E_{y},\,E_{z}\right)\propto \left(\cos {\frac {2\pi }{\lambda }}\left(ct-z\right)$$,\,\sin {\frac {2\pi }{\\pa }}\왼쪽(ct-z\오른쪽),\,0\오른쪽).$$}$

구체적인 예로 첫 번째 애니메이션의 원형 편광파를 들 수 있다. 이 관례를 이용하여, 그 파동은 오른손 엄지를 파장의 전파 방향과 같은 방향으로 가리킬 때, 그 손의 손가락이 필드의 시간 회전 방향과 같은 방향으로 구부러지기 때문에 오른손잡이로 정의된다. 선원의 관점에서 파장의 전파 방향을 같은 방향으로 바라보면 필드가 시계방향으로 회전하기 때문에 시계방향으로 원형으로 편광된 것으로 간주된다. 두 번째 애니메이션은 이와 같은 관례를 사용하여 왼손잡이 또는 시계 반대방향 조명의 애니메이션이다.

이 협약은 전기전자공학연구소(IEEE) 표준을 준수하며, 그 결과 일반적으로 공학계에서 사용된다.^[2][3][4]

양자 물리학자들도 이 손의 관습을 사용한다. 왜냐하면 그것은 입자의 스핀을 위한 손의 관습과 일치하기 때문이다.^[5]

라디오 천문학자들은 또한 1973년에 만들어진 국제천문연맹(IAU) 결의안에 따라 이 규약을 사용한다.^[6]

수신자의 입장에서 보면

이 대안적 협약에서 양극화는 수신자의 관점에서 정의된다. 이 관례를 이용하여 좌우 엄지손가락을 발원지 쪽으로 향하게 하고 전파방향에 반하게 한 다음 손가락 컬링을 필드의 공간 회전과 매칭하여 좌우 손바닥을 결정하게 된다.

이 관례를 사용할 때, 다른 관례와 대조적으로, 파형의 정의된 손은 공간에 있는 필드의 나사형 특성과 일치한다. 구체적으로 오른손 파동을 제때에 얼리면 오른손의 손가락을 나선 주위에 구부릴 때 엄지손가락은 회전감각으로 볼 때 나선의 진행 방향을 가리키게 된다. 모든 나사와 나선형의 성격상 손놀림을 결정할 때 엄지손가락을 어느 방향으로 가리키는지는 중요하지 않다는 점에 유의하십시오.

파동이 시계방향인지 시계방향 반시계방향으로 편광되어 있는지 판단할 때, 다시 수신기의 관점을 취하고, 전파방향에 반하여 원점을 바라보면서, 전장의 시간회전 방향을 관찰한다.

다른 관습과 마찬가지로 오른손잡이는 시계방향 회전에 해당하고 왼손잡이는 시계 반대방향 회전에 해당한다.

많은 광학 교과서들이 이 두 번째 규약을 사용한다.^[7][8] 국제순수화학연맹(IUPAC)뿐만 아니라 SPIE에서도^[9] 사용하고 있다.^[10]

두 규약 사용

앞서 언급했듯이, 이 두 협약에 대해 상당한 혼란이 있다. 일반적으로 공학, 양자물리학, 전파천문학계는 파동이 근원의 관점에서 관측되는 제1차 규약을 사용한다.^[3][5][6] 광학을 다루는 많은 물리학 교과서에서는 두 번째 규약이 사용되는데, 이 규약은 빛을 수신자의 관점에서 관찰하는 것이다.^[5][7]

혼동을 피하기 위해서는 양극화 문제를 논의할 때 '출처 관점에서 정의한 것' 또는 '수신자의 관점에서 정의한 것'을 명시하는 것이 좋다.

미국 연방표준 1037C의 기록 보관소는 양손에 대한 두 가지 상반된 규약을 제안한다.^[11]

FM 라디오

"순환 양극화"라는 용어는 주로 FM 라디오(미국에서는 87.5~108.0MHz)에서 사용되는 혼합 극성 신호를^{[citation needed]} 잘못 설명하기 위해 종종 사용된다. 이 신호는 수직 및 수평 구성 요소가 단일 또는 복합 어레이에 의해 동시에 전파된다. 이는 단 한 면의 양극화 신호보다 건물과 어려운 수신 구역에 더 큰 침투 효과를 내는 효과가 있다. 송신 안테나 설계의 송신기 및 기타 요인에 따라 수신기에서의 양극화가 일정하기는 하지만, 송신기로부터의 방향과 다른 요인에 따라 다르기 때문에 이는 양극화를 무작위 양극화라고 부르는 것이 더 적절한 예일 것이다. Stokes 매개 변수를 참조하십시오.
위의 "FM 라디오"라는 용어는 거의 독점적으로 수직 양극화를 사용하는 양방향 라디오(더 적절하게 지상파 모바일 라디오)가 아닌 FM 방송을 말한다.

이분법

원형 이분법(Circular Dichroism, CD)은 왼손과 오른손의 원형 편광의 차등 흡수법이다. 원형 이분법이란 분자의 광학적 이소체주의와 이차 구조를 결정하는 데 사용할 수 있는 분광법 형태의 기본이다.

일반적으로 이 현상은 광학적으로 활성하는 분자의 흡수 대역에서 나타날 것이다. 그 결과, 원형 이분자는 대부분의 생물학적 분자에 의해 나타나는데, 그 분자에 포함된 덱스트로타리(예: 일부 당분)와 레보로타리(예: 일부 아미노산) 분자 때문이다. 또한 주목할 만한 것은 2차 구조물이 각각의 분자에 구별되는 CD를 전달한다는 것이다. 따라서 단백질의 알파나선, 베타 시트 및 랜덤 코일 영역과 핵산의 이중나선에는 구조를 대표하는 CD 스펙트럼 서명이 있다.

또한 올바른 조건 하에서, 비-치랄 분자조차도 자기장에 의해 유도된 순환 이분법 즉 자기 순환 이분법을 보일 것이다.

발광

원형 편광 발광(CPL)은 루미노포레 또는 루미노포레 앙상블이 키랄일 때 발생할 수 있다. 방출의 양극화 정도는 비대칭 인자의 관점에서, 때로는 음이소트로피 인자로도 언급되는, 순환 이분법에 대한 것과 같은 방법으로 정량화된다. 이 값은 다음과 같이 지정된다.

$\\displaystyle g_{em}\\2\leftency\theta _{\mathrm {left}-\theta_{\mathrm {}+\theta _{\mathrm}}}}{\mathrmatrm {}}}}}}}}\right)}}}}}$

여기서 $\theta {\displaystyle {}_{}}$ ${\displaystyle {l\mathrm{}}_{}}$ e ${\displaystyle {\mathrm{e}}_{}}$ ${\displaystyle {\mathrm{t}}_{}}$ ${\${\$mathrm${left$}}}$은(는) 왼손의 원형 편광 광의 양자 수율에 해당하며$$, $\theta {\displaystyle {}_{}}$ ${\displaystyle {r\mathrm{}}_{}}$ ${\displaystyle {\mathrm{i}}_{}}$ ${\displaystyle {\mathrm{g}}_{}}$ ${\displaystyle {\mathrm{h}}_{}}$ ${\$\{\$mathrmatrm {rig}}}}}}$은(는)에$$ 해당한다. 따라서 순수하게 왼손 또는 오른손의 원형 양극화에 해당하는 g의_em 최대 절대값은 2이다. 한편 g가_em 달성할 수 있는 가장 작은 절대값은 선형 편광 또는 비편광에 해당하며 0이다.

수학적 설명

전기장과 자기장에 대한 전자파 방정식의 고전적인 사인파 평면파 용액은 다음과 같다.

${\displaystyle {\begin{aligned}\mathbf {E} (\mathbf {r} ,t)&=\left \,\mathbf {E} \,\right \mathrm {Re} \left\{\mathbf {Q} \left \psi \right\rangle \exp \left[i\left(kz-\omega t\right)\right]\right\}\\\mathbf {B} (\mathbf {r} ,t)&={\hat {\mathbf {z} }}\times \mathbf {E} (\mathbf {r} ,t)\end{aligned}}}$

여기서 k는 waennumber이다.

$\displaystyle \omega =ck}$

is the angular frequency of the wave; ${\displaystyle \mathbf {Q} =\left[{\hat {\mathbf {x} }},{\hat {\mathbf {y} }}\right]}$ is an orthogonal ${\displaystyle 2\times 2}$ matrix whose columns span the transverse x-y plane; and ${\displaystyle c}$ is the speed of light.

여기

${\displaystyle \왼쪽 \,\mathbf {E} \,\오른쪽 }$

필드의 진폭이며

${\displaystyle \rangele \{\stackrel {def}{}}}}{=}\\\\pmatrix}\cHB_{x}\i1}\end{pmatrix}={\cos \time \ex \i\lift(i\lipmpmatrix _{x}\right)\right)\\sin \theta \exp \left(i\lift _{y}\right)\end{pmatrix}}$

x-y 평면에서 정규화된 존스 벡터 입니다.

$\alpha {\displaystyle {}_{}}$ ${\displaystyle x_{}}$ ${\$ ${\displaystyle {\alpha }_{}}$x {\$displaystyle \alpha$_{$x}$에 대해 $\alpha {\displaystyle }$/ 2 ${\displaystyle \pi /$2$}$라디안으로$$ 회전하고$$$$ x 진폭이 y 진폭과 같을 경우 파형은 원형 편광이다. 존스 벡터는 다음과 같다.

${\displaystyle \cHBLE ={1\over{\sqrt{2}}:{\\pm i\end{pmatrix}}\exp \left(i\limits _{x}\오른쪽)}$

더하기 기호는 왼쪽 원형의 양극화를 나타내고, 빼기 기호는 오른쪽 원형의 양극화를 나타낸다. 원형 양극화의 경우 일정한 크기의 전기장 벡터가 x-y 평면에서 회전한다.

기본 벡터가 다음과 같이 정의되는 경우:

${\displaystyle \mathrm {R} \rangele \{\stackrel {def}{}}{}}\\sqrt{2}}: {\begin{pmatrix}1\-i\end{pmatrix}}}}}}$

및:

${\displaystyle \mathrm {L} \rangele \{\stackrel {def}{}}{}}\\sqrt{2}}: {\begin{pmatrix}1\i\end{pmatrix}}}}}}$

그런 다음 양극화 상태를 "R-L 기반"으로 다음과 같이 작성할 수 있다.

${\displaystyle \psi \rangele =\psi _{\mathrm {R} \mathrm {R} \rangele +\psi _{\mathrm {L} \mathrmartrm {L} \mathrmatrm {L} \rangele }}$

여기서:

${\displaystyle{\begin{정렬}\psi _{\mathrm{R}}~&,{\stackrel{\mathrm{def}}{)}}~{\frac{1}{\sqrt{2}}}\left(\cos\theta +i\sin \theta \exp \left(i\delta \right)\right)\exp \left(i\alpha_{x}\right)\\\psi _{L\mathrm{}}~&,{\stackrel{\mathrm{def}}{)}}~{\frac{1}{\sqrt{2}}}\left(\cos\theta -i\sin \theta \exp \left(i\delta \right)\rig.ht)\exp \left(i\put _{x}\오른쪽)\end{arged}}}$

및:

$\displaystyle \cHB =\display _{y}-\cHB _{x}.}$

안테나에

이 절에는 백과사전 항목에 대한 너무 많거나 지나치게 장황한 인용구가 수록되어 있다. 적절한 인용구들과 함께 중립적인 단어 요약으로 사실을 제시함으로써 기사를 개선하는 데 도움을 주기 바란다. Wikiquote에 직접 인용문을 전송하거나, 전체 작품에 대해 Wikisource에 전송하는 것을 고려한다. (2018년 4월)

여러 가지 다른 유형의 안테나 요소를 사용하여 원형 편광(또는 거의 그렇게) 방사선을 생성할 수 있다. 발라니스에 이어 쌍극성 요소를 사용할 수 있다.^[12]

"… 교차된 쌍극점 두 개가 두 직교 장 구성 요소를 제공한다... 만약 두 쌍둥이가 동일하다면, 정점을 따라 각 쌍둥이의 자기장 강도는 동일할 것이다... 또한, 두 쌍둥이가 90°의 시간 위상 차이(위상 4차)를 먹이면, 정점을 따라 양극화가 순환이 될 것이다.... 두 개의 다이폴에 의해 각각 방사된 두 직교장 구성 요소 사이의 90° 시간 위상 차이를 얻는 한 가지 방법은 다른 것보다 1/4 파장 길거나 짧은 전송 라인을 가진 두 개의 다이폴 중 하나를 공급하는 것이다." p.80;

또는 나선 요소:

"[축전 모드 또는 내화 모드에서] 원형 양극화를 달성하려면... 나선형의 원주 C는 ...여야 하며 C/파장 = 1은 최적에 가깝고 S = 파장/4" 페이지 571;

또는 패치 요소:

"…원소들에 대한 다양한 공급 배열이나 약간의 수정을 통해 원형 및 타원형 편광화를 얻을 수 있다... 두 직교 모드가 90°의 시간 위상 차이로 흥분할 경우 원형 양극화를 얻을 수 있다. 이는 패치의 물리적 크기를 조정하여 수행할 수 있다... 사각 패치 요소의 경우 이상적인 원형 양극화를 일으키는 가장 쉬운 방법은 인접한 두 모서리에 있는 요소를 공급하는 것이다... 4차 위상 차이는 원소에 90° 동력 분배기를 공급하여 얻는다." p.859.

양자역학에서

양자역학적 관점에서 볼 때 빛은 광자로 구성된다. 양극화는 빛의 회전각 운동량의 발현이다. 구체적으로는 양자역학에서 광자의 스핀 방향은 원형 편극광의 손길에 묶여 있으며, 광자의 빔의 스핀은 전자와 같은 입자의 빔의 스핀과 유사하다.^[13]

자연에서

자연에서 몇 가지 메커니즘만이 체계적으로 원형 편광 빛을 내는 것으로 알려져 있다. 1911년, 알버트 아브라함 미셸슨은 황금 스카라브 딱정벌레 크리시나 레스멘덴에서 반사된 빛이 우선적으로 좌극화된다는 것을 발견했다. 그 이후로, 원형 양극화는 크리시나 글로리오사와 ^[14]같은 몇몇 다른 스카라브 딱정벌레와 사마귀 새우 같은 갑각류에서 측정되었다. 이러한 경우에 근본적인 메커니즘은 치틴 큐티클의 분자 수준의 나선성이다.^[15]

반딧불이의 유충의 생물 발광도 1980년에 Photuris lucicrescens와 Photuris versicolor에서 보고된 바와 같이 원형 극성을 띤다. 반딧불이의 경우 유충의 좌우 등이 반대 감각의 편광광을 발산하는 것으로 밝혀졌기 때문에 양극화에 대한 미시적인 설명을 찾기가 더 어렵다. 저자들은 이 빛이 정렬된 광구체 내부의 불균형으로 인한 선형 양극화에서 시작하여 선형적으로 2중선 조직을 통과하면서 원형 양극화를 잡아낸다고 제안한다.^[16]

수공기 인터페이스는 또 다른 순환 양극화의 원천을 제공한다. 다시 표면 쪽으로 흩어지는 햇빛은 선형적으로 편광된다. 만약 이 빛이 완전히 내적으로 반사되면, 수직 구성 요소는 위상 변화를 겪는다. 위를 올려다보는 수중 관찰자에게 스넬의 창밖의 희미한 빛은 그러므로 (부분적으로는) 원형 극성을 띠게 된다.^[17]

자연에서 원형 양극화의 약한 원천은 별빛의 원형 양극화에서처럼 선형 편광기에^{[dubious – discuss]} 의한 다중 산란과 원형 이분법에 의한 선택적 흡수가 있다.

별과 펄서의 전파 방출은 강하게 원형으로 편광될^{[citation needed]} 수 있다.

사마귀 새우 2종은 원형 편광 검출이 가능한 것으로 알려졌다.^[18][19]

참고 항목

• 편광기
• 3D 필름
• 치랄리티
• 전자파 방정식의 사인파 평면파 용액
• 별빛 양극화
• 웨이브플레이트

참조

외부 링크

• 원형 편광: 딱정벌레 및 디스플레이
• 사마귀새우와 원형 양극화에 관한 토막글
• 원형극화 애니메이션 (유튜브에서)
• 선형 및 타원 편광화를 이용한 원형극화 비교
• 거울에 의한 원형 편광 광선의 손놀림 반전. 데모 – 단순하고 저렴하며 유익한 사용

추가 읽기

• Jackson, John D. (1999). Classical Electrodynamics (3rd ed.). New York: Wiley. ISBN 978-0-471-30932-1.
• Born, M. & Wolf, E. (1999). Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light (7th ed.). Cambridge: Cambridge University Press. ISBN 978-0-521-64222-4.