그룹 지연 및 위상 지연

신호 처리에서 그룹 지연은 신호의 다양한 사인파 성분의 진폭 봉투의 시간 지연이며, 각 성분에 대한 주파수의 함수다. 위상 지연은 대조적으로 진폭 엔벨롭의 시간 지연과 반대로 위상의 시간 지연이다.

신호의 모든 주파수 구성요소는 증폭기, 확성기 등의 장치를 통과하거나 공기와 같은 공간이나 매체를 통해 전파될 때 지연된다. 이 신호 지연은 기기가 선형 위상이라는 특성을 가지지 않는 한 다양한 주파수에 대해 달라질 것이다. 지연 변동은 다중 주파수 구성요소로 구성된 신호들이 기기의 출력에서 동일한 시간만큼 지연되지 않기 때문에 왜곡을 겪게 된다는 것을 의미한다. 이것은 신호의 모양을 변화시키고, 또한 일정한 지연이나 스케일 변화도 추가로 변화시킨다. 지연 편차가 충분히 크면 아날로그 반송파 신호에서 디지털 정보가 삭제될 때 오디오의 충실도가 저하되거나 ISI(기호간 간섭)와 같은 문제가 발생할 수 있다. 고속 모뎀은 일정하지 않은 그룹 지연을 보상하기 위해 적응형 이퀄라이저를 사용한다.

증폭기나 통신 시스템과 같은 장치의 경우, 그룹 지연과 위상 지연은 시간 지연의 특성을 나타내는 장치 성능 속성으로서, 신호의 다양한 주파수 성분이 입력에서 출력까지 장치를 통과하는 시간의 양이다. 이 타이밍이 특정 요건을 충분히 충족하지 못하면 기기가 신호 왜곡에 기여할 것이다. 예를 들어, 충분한 왜곡은 비디오나 오디오의 충실도가 떨어지거나 디지털 비트 스트림의 비트 오류율이 높다는 것을 의미한다.

위상 지연은 개별 주파수 구성 요소의 장치 또는 시스템 시간 지연을 직접 측정한다. 원래 신호 인텔리전스를 복구하기 위해 감속해야 하는 변조된 신호의 경우, 감속된 신호의 시간 지연을 결정하기 위해 변조된 신호와 함께 그룹 지연을 사용해야 한다.

이 기사에서 설명하는 배경 이론은 기기의 위상 지연 및 그룹 지연 속성을 정확하게 계산할 수 있는 장치의 위상 응답 속성에 관한 이론이다. 이어서 기사는 이와 관련된 장치 속성의 이론과 사용 사례를 설명한다.

소개

위상지연

선형 시간 불변성(LTI) 시스템 또는 장치는 장치의 위상 지연을 정확하게 계산할 수 있는 위상 응답 속성을 갖는다. 위상 지연은 신호의 다양한 주파수 성분의 시간 지연을 제공한다. 위상 지연은 주파수 시간 지연의 함수이기 때문에, 기능 그래프의 평탄도에서 벗어나면 다양한 신호 주파수 성분들 간의 시간 지연 차이를 나타낼 수 있으며, 이 경우 그러한 차이는 신호 왜곡에 기여하게 되며, 이는 출력 신호 파형 모양이 그것과 다른 것으로 나타난다. 입력 신호의 일반적으로 위상 지연 속성은 기기 입력이 변조된 신호인 경우 유용한 정보를 제공하지 않는다. 그러기 위해서는 그룹 지연을 이용해야 한다.

그룹지연

그림 1 - 외부 및 내부 LTI 장치

그룹 지연에 대한 기본 사용 사례는 그림 1에 설명되어 있으며, 그림 1은 그 자체가 내부(적색 블록) LTI 장치를 포함하고 있는 외부 LTI 장치를 보여준다. 신호의 한 버전은 원래 베이스밴드 주파수 범위의 주파수 구성요소로 구성되며, 동일한 정보를 전달하는 다른 버전은 변조기에 의해 더 높은 패스밴드 주파수 범위로 이동된 주파수 구성요소로 구성되는 변조된 신호다. 디모듈레이터는 그 반대로 주파수를 원래의 베이스밴드 범위로 다시 이동시킨다. 이상적으로 출력(베이스밴드) 신호는 입력(베이스밴드) 신호의 시간 지연 버전이며 출력의 파형 모양이 입력의 파형 모양과 동일하다.

제한된 상황에서 적색 내부 장치의 그룹 지연 속성은 외부 장치 단계 지연에 대한 대용물이 될 수 있다. 외부 장치 단계 지연은 의미 있는 성능 메트릭이다. 예를 들어, 내부 적색 장치 그룹 지연이 완전히 평평한 경우 외부 장치도 완전히 평평한 위상 지연의 이상을 가지게 될 것이며, 이 경우 내부 장치의 상이한 위상 응답에 의해 전적으로 결정되는 외부 LTI 장치의 위상 응답으로 인한 왜곡의 기여가 제거된다. 이 경우, 내부 적색 장치의 그룹 지연과 외부 장치의 위상 지연은 모두 베이스밴드 입력에서 베이스밴드 출력까지의 신호 시간 지연에 대해 동일한 수치를 제공한다. 내측(빨간색) 장치의 경우 매우 평평하지 않은 위상 지연(단, 플랫 그룹 지연)이 가능한 반면, 외부 장치의 경우 완벽하게 평평한 위상 지연이 이상적이라는 점에 유의해야 한다. 이는 LTI 기기 설계에서 플랫 위상 지연보다 플랫 그룹 지연을 달성하기가 더 쉽기 때문에 다행이다.

흔히 라디오 시스템의 경우처럼, 그림 1의 빨간색 LTI 장치는 송신 끝과 수신 끝의 두 개의 LTI 장치를 계단식으로 나타낼 수 있다.

배경

신호의 주파수 구성 요소

주기적인 신호의 경우, 주파수 성분은 시간 기반 주파수와 위상을 포함하는 특성을 가진 사인파이다.

기본 사인파 생성

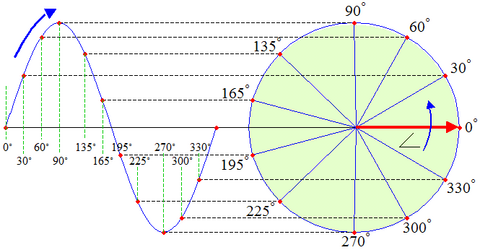
사인파(synuse)는 시간 기반 주파수 속성을 포함하거나 포함하지 않고 그림과 같이 원에 의해 생성된다. 이 예에서 사인파(sincyoid)는 신트리그 함수를 사용하여 추적되는 사인파다.

원의 사인파 추적: y=sin(x) 이 예에서는 sin trig 함수를 사용한다. 사인파 및 단위 원 모두에 대해 종속 출력 변수 y는 수직 축에 있다. 사인파 전용의 경우 도 단위의 각도는 수평축의 독립 입력 변수 x이다. 단위 원에만 대해 도 단위의 각도는 독립 입력 값 x이며, 가로축과 적색 벡터 사이에 만들어진 다이어그램에서 실제 각도로 표현되며, 현재 영상에서 0도에 있지만 어느 각도에서도 될 수 있다.

미디어 재생

회전 벡터 () 함수를 추적한다. 1단계 재생 버튼을 누르십시오. 2단계 최대화 3단계 WebM 소스 선택

증가하는 각도 x가 원을 중심으로 완전한 CCW 회전을 할 때 함수 패턴의 한 사이클이 생성된다. 360도 이상으로 각도를 더 늘리면 단순히 원을 중심으로 다시 회전하여 또 다른 사이클을 완성하는데, 이때 각 사이클이 동일한 패턴을 반복하여 기능을 주기적으로 만든다. ("회전 벡터..."를 참조하십시오.왼쪽의 「애니메이션」) 각도 값에는 한계가 없고, 따라서 패턴 자체가 반복되는 횟수 또한 한계가 없다. 이 때문에 사인파에는 시작도 끝도 없다. 사인 함수는 trig 함수 sin(x)과 cos(x) 중 하나 또는 둘 다에 기초한다.

이론

LTI(Linear-time-invariant) 시스템 이론, 제어 이론 및 디지털 $\displaystyle x(t)$ 아날로그 신호 처리에서 LTI 시스템의 입력 신호, $\displaystyle x(t)$ ( t $\displaystyle x(t)$ ) ${\$ 과 $\displaystyle x(t)$ 출력 신호, $\displaystyle y(t)$ ( $\displaystyle y(t)$ ) ${\$ 사이의 관계는 다음과 같은 콘볼루션 작업에 의해 제어된다.

y(t)=(h*x)(t)\\\stackrel {\mathrm {def}{=}\int_{-\infit }^{\infit }x(u)h(t-u)\,du

또는 주파수 영역에서는

[\displaystyle Y(s)=H(s)X\,}

, where

X(s)={\mathcal{L}{{}x(t){\Big \{}}\\\\stackrel {\mathrm {def}{=}}\int _{-\infit }^{-\x(t)^{-st}\,dt

Y(s)={\mathcal{L}{{}y(t){\Big \{}}\\\\stackrel {\mathrm {def}{=}}\int _{-\infit }^{-\infit}^{-\y(t){-st}\,dt

그리고

H(s)={\mathcal {L}}{\Big \{}h(t){\Big \}}\ {\stackrel {\mathrm {def} }{=}}\ \int _{-\infty }^{\infty }h(t)e^{-st}\,dt

.

Here $\displaystyle h(t)$ is the time-domain impulse response of the LTI system and $\displaystyle X(s)$ , $\displaystyle Y(s)$ , $\displaystyle H(s)$ , are the Laplace transforms of the input ${\displaystyle \$ $displaystyle x($ $\displaystyle y(t)$ $)}$ , $\displaystyle y(t)$ y $\displaystyle y(t)$ ( t $\displaystyle y(t)$ ) ${\$ , 임펄스 응답 $\displaystyle h(t)$ ( $\displaystyle h(t)$ ) ${\$ $\displaystyle h(t)$ 각각 . $\displaystyle H(s)$ ( $\displaystyle H(s)$ ) ${\$ 은 $\displaystyle H(s)$ (는) LTI 시스템의 전송 함수로 불리며, 임펄스 $\displaystyle h(t)$ h $\displaystyle h(t)$ ( $\displaystyle h(t)$ ) ${\$ 처럼 $\displaystyle h(t)$ LTI 시스템의 입력-출력 특성을 완전히 정의한다.

그러한 시스템이 사인파 주파수 $\displaystyle a(t)>0$ {\displaystyle $\displaystyle a(t)0}$ 을 $\displaystyle a(t)>0$ (를 $)$ 갖는 사인파 신호에 의해 구동된다고 가정해 보자. 이 신호는 사인파의 주파수 $\displaystyle \omega$ $\displaystyle \omega$ {\ $displaystyle \displaystyle \omega$ }. 수학적으로 이것은 준시뉴소이드 주행 신호의 형태가 있다는 것을 의미한다.

(\displaystyle x(t)=a(t)\cos(\omega t+\theta )\ }

그리고 천천히 변화하는 진폭 $\displaystyle a(t)$ ( t $\displaystyle a(t)$ ) {\ $displaystyle \displaystyle$ a( $t)}은$

\왼쪽 {\frac {d}{dt}\log {\big (}a(t){\big )}\오른쪽 \ll \omega \.

그런 다음 그러한 LTI 시스템의 출력은 다음과 같이 매우 근사하게 계산된다.

y(t)={\big }H(i\omega){\big }\a(t-\tau _{g})\cos {\big(t-\tau _{\pi }+\ta {\big )}\;

여기에서 그룹 지연과 위상 지연 각각 $\displaystyle \tau _{\phi }$ $\displaystyle \tau _{g}$ g ${\$ $phi$ $},$ $\displaystyle \tau _{\phi }$ $\displaystyle \tau _{g}$ ${\$ phi $\displaystyle \tau _{\phi }$ }}}은(잠재적으로는 각도 주파수 $\displaystyle \omega$ ${\$ 의 함수)로 $\displaystyle \tau _{g}$ 주어진다. $\displaystyle \omega$ 영 교차로에서 알 수 있듯이 사인파이는 위상 지연에 의해 시간적으로 지연되며, $\displaystyle \tau _{\phi }$ { { ${\$ $\displaystyle \tau _{\phi }$ 사인파 봉투는 그룹 지연 $\displaystyle \tau _{g}$ $\displaystyle \tau _{g}$ ${\$ \displaystyle \ $tau_{g}$ 에 의해 시간 내에 지연된다 $\displaystyle \tau _{g}$

선형 위상 시스템(반복되지 않는 이득 포함)에서 $\displaystyle \tau _{g}$ $\displaystyle \tau _{g}$ g ${\$ 및 $\displaystyle \tau _{\phi }$ ${\$ }}}은 $($ 즉 $\displaystyle \tau _{\phi }$ , $\displaystyle \omega$ ${\$ 와는 무관하며, 공통 값은 시스템의 전체 지연과 동일하다.시스템의 래핑된 위상 변화( ( - $\displaystyle -\omega \tau _{\phi }$ $\displaystyle -\omega \tau _{\phi }$ ${\$ - $\omega \tau _{\$ $phi })$ 는 음수이며, 주파수 $\displaystyle \omega$ 으로 크기가 선형적으로 증가한다 $\displaystyle \omega$

보다 일반적으로 단위 진폭의 복잡한 정현상으로 $\displaystyle H(s)$ 되는 전송 함수 $\displaystyle H(s)$ ( s $\displaystyle H(s)$ ) {\ $displaystyle \displaystyle H}$ 을(를) 갖는 LTI 시스템의 경우,

x(t)=e^{i\omega t}\

생산량은

{\begin{aligned}y(t)&=H(i\omega )\ e^{i\omega t}\ \\&=\left({\big  }H(i\omega ){\big  }e^{i\phi (\omega )}\right)\ e^{i\omega t}\ \\&={\big  }H(i\omega ){\big  }\ e^{i\left(\omega t+\phi (\omega )\right)}\ \\\end{aligned}}\

위상 편이 $\displaystyle \phi$ ${\$ 인 $\displaystyle \phi$ 경우

\phi(\omega)\\\\\stackrel {def}{}}{=}\\arg \left\{}H(i\omega)\right\}\;

또한 그룹 지연 , $\displaystyle \tau _{\phi }$ ${\$ 위상 지연 delay ${\$ $\displaystyle \tau _{\phi }$ 은 주파수에 따라 다르며 적절히 $\displaystyle \phi$ 포장되지 않은 위상 편이 shift ${\$ 에서 계산할 수 있다.

\tau _{g}(\omega )=-{\frac {d\phi(\omega)}{d\omega }\}

\tau _{\phi }(\omega )=-{\frac {\phi (\omega )}{\omega }}\

)

\tau _{\phi }(\omega )=-{\frac {\phi (\omega )}{\omega }}\

= -

\tau _{\phi }(\omega )=-{\frac {\phi (\omega )}{\omega }}\

(

\tau _{\phi }(\omega )=-{\frac {\phi (\omega )}{\omega }}\

)

\tau _{\phi }(\omega )=-{\frac {\phi (\omega )}{\omega }}\

displaystyle \tau _{\

pau _{\

pi }(\omega )=-{\frac {\pi(\omega )}{\omega }\}}.

즉, "그룹 지연은 각도 주파수에 관한 스펙트럼 단계의 파생물로 정의할 수 있다"(^[1]즉시 주파수와 비교)는 것이다.

광학에서 그룹 지연

집단지연은 물리학에서, 특히 광학에서 중요하다.

그룹 지연은 각도 주파수에 대한 총 위상 편이동의 변화율이다.

\tau _{g}=-{\frac {d\phi }{d\omega}}

디바이스 또는 전송 매체를 통해

\phi

\phi

은

\phi

(는) 라디안의 총 위상 편이이고,

\omega

{\displaystyle

\opega

}

은

\omega

(는)

2\pi f

2\pi f

라디안의 각도 주파수로

2\pi f

여기서

f

2\pi f

{\displaystystyle f}

은 주파수(초 단위로 측정된 경우 헤르츠)이다

f

.

광섬유에서 그룹 지연은 주어진 모드의 그룹 속도로 이동하는 광학전력에 필요한 전송시간이다. 광섬유 분산 측정의 경우 관심 수량은 단위 길이당 그룹 지연이며, 이는 특정 모드의 그룹 속도의 역수다. 광섬유를 통한 신호의 그룹 지연 측정은 광섬유의 다양한 분산 메커니즘으로 인한 파장 의존성을 나타낸다.

그룹 지연은 종종 모든 주파수에서 일정하게 유지되는 것이 바람직하다. 그렇지 않으면 신호의 일시적 얼룩이 있다. Because group delay is ${\textstyle \tau _{g}(\omega )=-{\frac {d\phi }{d\omega }}}$ , it therefore follows that a constant group delay can be achieved if the transfer function of the device or medium has a linear phase response (i.e., ${\displaystyle \phi (\omega )=\phi (0)$ - $\tau _{g}\omega}$ 그룹 지연 $\tau _{g}$ $\tau _{g}$ ${\$ 이 상수인 $\tau _{g}$ 경우 $\phi (\omega )=\phi (0)-\tau _{g}\omega$ ). 위상의 비선형성 정도는 상수로부터 그룹 지연의 편차를 나타낸다.

오디오의 그룹 지연

그룹 지연은 오디오 분야와 특히 사운드 재생 분야에서 어느 정도 중요하다. 오디오 재생 체인의 많은 구성 요소들, 특히 확성기와 다방향 확성기 크로스오버 네트워크는 오디오 신호에 그룹 지연을 도입한다. 따라서 특히 오디오 체인이 높은 충실도의 재현을 제공하도록 되어 있는 경우 주파수와 관련하여 그룹 지연의 청각성의 임계값을 아는 것이 중요하다. 청각성 표의 최고 임계값은 Blauert & Laws(1978년)에 의해 제공되었다.

빈도	임계값	기간(주기)
500Hz	3.2ms	1.6
1kHz	2ms	2
2kHz	1ms	2
4kHz	1.5 ms	6
8kHz	2ms	16

플래너건, 무어, 스톤은 1, 2 및 4 kHz에서 그룹 지연이 약 1.6 ms를 반복되지 않는 조건에서 헤드폰으로 들을 수 있다고 결론짓는다.^[2]

실제 시간 지연

송신 기기는 시간 지연이 전기 신호의 주파수와 무관한 경우 참 시간 지연(TTD)이 있다고 한다.^[3]^[4] TTD는 무손실 및 저손실, 분산 무손실 전송 라인의 중요한 특성이다. TTD는 펄스 작동 중 펄스 확대와 같은 신호 왜곡이 거의 없는 넓은 순간 신호 대역폭을 허용한다.

참고 항목

오디오 시스템 측정
베셀 필터
눈 패턴
그룹 속도 — "매체에서 빛의 그룹 속도는 단위 길이당 그룹 지연의 역행이다."^[5]

참조

이 문서에는 일반 서비스 관리 문서의 공용 도메인 자료가 포함되어 있다. "Federal Standard 1037C".

^ Paschotta, Rü (2020-03-14). "Spectral Phase". RP Photonics Encyclopedia. Retrieved 2021-06-07.
^ Flanagan, Sheila; Moore, Brian C. J.; Stone, Michael A. (2005), "Discrimination of Group Delay in Clicklike Signals Presented via Headphones and Loudspeakers", Journal of the Audio Engineering Society, 53 (7/8): 593–611
^ "True Time Delay". Microwaves101, IEEE.
^ Julius O. Smith III. "Phase Delay and Group Delay". Music 320 Background Reader. Department of Electrical Engineering, Stanford University.
^ "Group Delay".

Blauert, J.; Laws, P. (May 1978), "Group Delay Distortions in Electroacoustical Systems", Journal of the Acoustical Society of America, 63 (5): 1478–1483, Bibcode:1978ASAJ...63.1478B, doi:10.1121/1.381841

외부 링크

[Paschotta2020-1] Paschotta, Rü (2020-03-14). "Spectral Phase". RP Photonics Encyclopedia. Retrieved 2021-06-07.

[2] Flanagan, Sheila; Moore, Brian C. J.; Stone, Michael A. (2005), "Discrimination of Group Delay in Clicklike Signals Presented via Headphones and Loudspeakers", Journal of the Audio Engineering Society, 53 (7/8): 593–611

[3] "True Time Delay". Microwaves101, IEEE.

[4] Julius O. Smith III. "Phase Delay and Group Delay". Music 320 Background Reader. Department of Electrical Engineering, Stanford University.

[5] "Group Delay".

[1]

[2]

[3]

[4]

[5]

Search