관련 미분 방정식에 대한 해군
베셀 기능은 원형 드럼 진동 모드의 방사형 부분입니다. 처음 에 수학자 다니엘 베르누이 에 의해 정의되고 그 후에 프리드리히 베셀에 의해 일반화되는 베셀 함수는 베셀의 미분 방정식의 표준 해 y (x )
x 2 d 2 y d x 2 + x d y d x + ( x 2 − α 2 ) y = 0 \displaystyle x^{2}{\frac {d^{2}y}+xfrac {dy}{flac}+\left(x^{2}-\alpha^{2}\right)y=0} 임의의 복소수α 의 경우 베셀 함수의 순서 입니다.α와 -α 는 동일한 미분 방정식을 생성 하지만, β의 함수 가 대부분 매끄러운 함수가 되도록 이 두 값에 대해 서로 다른 β 함수를 정의하는 것이 일반적이다.
가장 중요한 경우는 α가 정수 또는 반정수인 경우 입니다. 정수α 에 대한 베셀 함수는 원통 좌표 에서 라플라스 방정식 의 해답에 나타나기 때문에 원통 함수 또는 원통 고조파 한다 .헬름홀츠 방정식을 구좌표 로 풀었을 때 반정수α 를 갖는 구면 베셀 구한다
베셀 기능의 응용 베셀 함수는 사인 함수를 일반화한 것입니다. 두께가 가변적인 스트링의 진동, 장력이 가변적인(또는 두 가지 조건을 동시에 갖는), 특성이 가변적인 매체에서의 진동, 디스크막의 진동 등으로 해석할 수 있다.
베셀 방정식은 라플라스 방정식 과 헬름홀츠 방정식에 대한 분리 가능한 해답을 원통형 또는 구면 좌표에서 찾을 때 발생합니다. 따라서 베셀 함수는 파동 전파와 정적 전위의 많은 문제에 특히 중요하다. 원통 좌표계로 문제 해결에서, 1;구면에서 한(α)n+.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{half-integer 주문을 지급 받은 정수 명령(α)n)의 베셀 함수를 얻습니다.디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{.국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1/2컵. 예를 들어 다음과 같습니다.
베셀 기능은 신호 처리와 같은 다른 문제에서도 나타납니다(예: FM 합성, 카이저 창 또는 베셀 필터 참조 ).
정의들 이 방정식은 2차 선형 미분 방정식이므로 두 개의 선형 독립 솔루션이 있어야 합니다. 다만, 상황에 따라서는, 이러한 솔루션의 다양한 제형이 편리합니다. 다음 표에 다양한 변형을 정리하고 다음 섹션에서 설명합니다.
제2종의 베셀함수와 제2종의 구형 베셀함수는 각각 Y, [1] [2] y 가n 아닌n N, n 으로n n 나타나기도 한다.
Jα J(x ) 로 표시 α 제1종 베셀 함수는 베셀의 미분 방정식의 해이다. 정수 또는 양 의 α의 경우, 첫 번째 종류의 베셀 함수는 원점(x 0 )에서 유한한 반면, 음의 비표준 α의 경우, 첫 번째 종류의 베셀 함수는 x가 0에 가까워짐에 따라 분리가 된다. 함수를 x = 0 주위 급수 팽창으로 정의할 수 있으며, 프로베니우스 방법을 베셀 [3]
J α ( x ) = ∑ m = 0 ∞ ( − 1 ) m m ! Γ ( m + α + 1 ) ( x 2 ) 2 m + α , {\displaystyle J_{\alpha }(x)=\sum _{m=0}^{\infty}{\frac {(-1)^{m}}{m! \Gamma(m+\alpha +1)}{\left({\frac {x}{2}}\right)}^{2m+\alpha}}} 여기서 δ(z ) 는 감마 함수로, 요인 함수의 비정수 값으로의 시프트 일반화이다. 첫 번째 종류의 베셀 함수는 α가 정수이면 전체 함수 이고, 그렇지 않으면 0에서 특이점을 갖는 다치 함수이다. 베셀 함수의 그래프는 x 1 2 ( 아래 참조) 진동 또는 큰 x를 제외하고 일반적으로 주기적이지 않습니다. (계열은 -J1 (x ) 가 도함수임을 나타냅니다.) e of 0 (x ) 는 -sin cos x(x ) 의n 도함수는 아래의 항등식 에 의해 J(x ) 로n ± 1
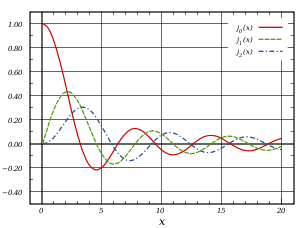
정수 차수α 0, 1 , 2 에 대한 첫 번째 종류의 베셀 함수 Jα (x ) 정수 α가 아닌 경우, 함수α (x ) 와−α J(x ) 는 선형 독립적이며, 따라서 미분 방정식의 두 가지 해이다.반면 정수 차수 n의 경우 다음 관계가 유효하다(감마 함수는 각 비양수 [4]
J − n ( x ) = ( − 1 ) n J n ( x ) . {\displaystyle J_{-n}(x)=param1)^{n}J_{n}(x) }
이는 두 솔루션이 더 이상 선형 독립적이지 않음을 의미합니다. 이 경우, 두 번째 선형 독립 해는 아래에서 논의한 것처럼 두 번째 종류의 베셀 함수인 것으로 밝혀졌다.
베셀 적분 정수값 n 에 대한 베셀 함수의 또 다른 정의는 적분 [5]
J n ( x ) = 1 π ∫ 0 π 왜냐하면 ( n τ − x 죄 τ ) d τ = 1 2 π ∫ − π π e i ( n τ − x 죄 τ ) d τ , {\displaystyle J_{n}(x)=black {1}{\pi }}\int _{0}^{\pi }\cos(n\black -x\sin \cos(n\cos)},d\black =black {1}{2\pi }{\pi } ^{i(n\pi }\csin } }) '한센-베셀 공식'[6]
이것은 베셀이 사용한 접근법이었고, 그는 이 정의에서 함수의 몇 가지 특성을 도출했다. 정의 는 Re(x ) > [5] [7] [8] [9] [10] 0 의 경우 슐레플리의 적분 중 하나에 의해 정수 이외의 차수로 확장될 수 있다.
J α ( x ) = 1 π ∫ 0 π 왜냐하면 ( α τ − x 죄 τ ) d τ − 죄 α π π ∫ 0 ∞ e − x 쌍곡선 정현. t − α t d t . {\displaystyle J_{\alpha }(x)=syfrac {1}{\pi }}\int _{0}^{\pi }\cos(\alpha \alpha - x \sin \pi }{\pi }}\int _0}{\frac - {\alpha } tx } }
초기하 급수와의 관계 베셀 함수는 일반화된 초기하 급수의 관점 에서[11]
J α ( x ) = ( x 2 ) α Γ ( α + 1 ) 0 F 1 ( α + 1 ; − x 2 4 ) . {\displaystyle J_{\alpha }(x)=frac {leftfrac {x}{\alpha}}{\Gamma(\alpha +1)}}}\ ;_{0}F_{1}\left(\alpha +1;-\frac {x^{2}}{4}}\오른쪽). }
이 표현은 베셀-클리퍼드 함수의 관점에서 베셀 함수의 개발과 관련이 있다.
라게르 다항식과의 관계 Laguerre 다항식k L과 임의로 선택된 매개변수 t에 관하여, 베셀 함수는 다음과 같이 표현될[12]
J α ( x ) ( x 2 ) α = e − t Γ ( α + 1 ) ∑ k = 0 ∞ L k ( α ) ( x 2 4 t ) ( k + α k ) t k k ! . {\displaystyle {J_{\alpha }(x)}{\left\frac {x}{\alpha}}=sum _{Gamma (\alpha +1)}{\infty }{\frac {\frac }{\frac }{\frac {e^{-t}}}}}}{\gamfrac {e^{e^{-t}}}}}}}}{\Gamma}}}{\Gamfrac {e framma}}}}{ }}.}
Yα . Y( x ) 로α 표시 α 두 번째 종류의 베셀 함수는 원점( x = 0 )에 특이점을 가지며 다중값 인 베셀 미분 방정식의 해이다. 이것들은 때때로 H. M . Weber 에 의해 도입되어 베버 함수라고 불리기 도 하고, 또한 칼 [13] 노이만의 이름 을 따서 노이만 함수라고도 불린다.
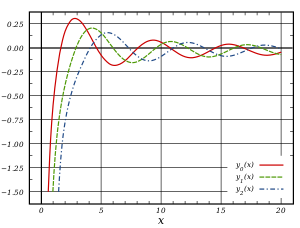
정수 차수α 0, 1 , 2 에 대한 두 번째 종류 α 베셀 함수 Y(x ) 그림 비정수α 의 경우 Y ( x)는α J ( x)와α 다음과 같이 관련된다.
Y α ( x ) = J α ( x ) 왜냐하면 ( α π ) − J − α ( x ) 죄 ( α π ) . {\displaystyle Y_{\alpha }(x)=vsfrac {J_{\alpha }(x)\cos(\alpha \pi)-J_{-\alpha }(x)}{\sin(\alpha \pi}}}}. }
정수차수 n의 경우, 함수는 비정수 α가 n 을 나타내는 경향이 있으므로 한계를 취함으로써 정의된다.
Y n ( x ) = 림 α → n Y α ( x ) . \displaystyle Y_{n}(x)=\lim _{\alpha \to n}Y_{\alpha }(x) }
만약 n이 음수가 아닌 정수라면, 우리는 다음과[14]
Y n ( z ) = − ( z 2 ) − n π ∑ k = 0 n − 1 ( n − k − 1 ) ! k ! ( z 2 4 ) k + 2 π J n ( z ) 인 z 2 − ( z 2 ) n π ∑ k = 0 ∞ ( ψ ( k + 1 ) + ψ ( n + k + 1 ) ) ( − z 2 4 ) k k ! ( n + k ) ! {\displaystyle Y_{n}(z)=-{\frac {2}}{-n}}{\pi }}\sum _{k=0}^{n-1}{\frac {(n-k-1)! }{k!}\left({\frac {z^{2}}{4}}\right)^{k}+{\frac {2}{\pi }}J_{n}(z)\ln {{frac {z}{2}}-{\frac {z}\rac {z}\right}) ^{n}}{\pi }}\sum _{k=0}^{\infty }(\psi (k+1)+\psi (n+k+1)) (\frac {z^{2}}{4}\오른쪽) ^{k}{k!(n+k)! }}}
여기서 z displaystyle \psi (z) 감마 [15] 로그 도함수 인 디감마 함수이다.
대응하는 적분식도 있습니다(Re (x )> [16] 경우 ).
Y n ( x ) = 1 π ∫ 0 π 죄 ( x 죄 θ − n θ ) d θ − 1 π ∫ 0 ∞ ( e n t + ( − 1 ) n e − n t ) e − x 쌍곡선 정현. t d t . {\displaystyle Y_{n}(x)=frac {1}{\pi }}\int _{0}^{\pi }\sin \theta }, d\theta - {1}{\pi }\int _{0}^{\infty }\left(e^{n}-{n}^{n}) }
n = 0 인 경우
Y 0 ( x ) = 4 π 2 ∫ 0 1 2 π 왜냐하면 ( x 왜냐하면 θ ) ( e + 인 ( 2 x 죄 2 θ ) ) d θ . {\displaystyle Y_{0}\left(x\right)=pi frac {4}{\pi ^{2}\int _{0}^{{2}\pi }\cos \left(x\cos \theta \right)\left(e+\ln \left(2xcsin }^2\ta\ta\right).
Yα (x )때 베셀 방정식의 두 번째 선형 독립해로서 필요하다.하지만 Y(x ) 는α 그 이상의 의미가 있습니다. J(x ) 의α "자연스러운" 파트너로 간주할 수 있습니다. 아래 항켈 함수에 대한 하위 절도 참조하십시오.
α가 정수일 경우 , 게다가 제1종 함수의 경우와 마찬가지로 다음과 같은 관계가 유효하다.
Y − n ( x ) = ( − 1 ) n Y n ( x ) . {\displaystyle Y_{-n}(x)=param1)^{n} Y_{n}(x) }
Jα (x )α Y(x ) 는 모두 음의 실축을 따라 절단된 복소평면상 의 x 의 정칙함수 이다.α가 정수일 때 , 베셀 함수 J는 x의 전체 함수 이다. 만약 x가 0이 아닌 값으로 고정된다면, 베셀 함수는 α의 전체 함수이다.
α가 정수일 때 두 번째 종류의 베셀 함수는 Fuchs 정리 에서의 두 번째 종류의 해법의 한 예이다.
H (1) α H (2) α 베셀 방정식에 대한 두 선형 독립 해법의 또 다른 중요한 공식은 다음과 같이 정의된[17] 제1종 과 제2종 (1) α (x ) 및 (2) α (x ) 의 행켈 함수 이다.
H α ( 1 ) ( x ) = J α ( x ) + i Y α ( x ) , H α ( 2 ) ( x ) = J α ( x ) − i Y α ( x ) , 디스플레이 스타일 H_{\alpha }^{(1)(x)&=J_{\alpha }(x)+iY_{\alpha }(x),\H_{\alpha }^{(2)(x)&=J_{\alpha }(x)-iY_{\alpha }(x),\end} 정렬 여기 서 i는 상상 의 단위입니다.이러한 선형 조합은 세 번째 종류의 베셀 함수 라고도 하며, 베셀 미분 방정식의 두 개의 선형 독립 해입니다. 그것들 은 헤르만 행켈의 이름 을 따서 지어졌다.
이러한 선형 조합의 형태는 점근 공식이나 적분 표현과 같은 수많은 단순해 보이는 특성을 충족합니다. 여기서 "단순"은 형태 i f (x) 실제 x>0{\displaystyle x>0}에 대한 내용은 Jα()){\displaystyle J_{\alpha}())}, Yα()){\displaystyle Y_{\alpha}())}은 실수를 사용한, 베셀 함수의 1번째 숫자와 2번째 종류의 실제 및 허수 부분 각각 첫번째 항켈 함수와 현실과 부정적인 상상의 한 부분입니다.그 두 번째 항켈 함수. 그러므로 위의 공식 오일러의 공식의 전후, 전 남편으로{\displaystyle e^{\pm ix}x e±}와 J는 α({\displaystyle J_{\alpha}())}, cos()){\displaystyle \cos())}을 Yα()){\displaystyle Y_{\alpha}())}, 죄()){\displaystyle \sin())}, H(1)α()), H(2)α())으로 대신하고 있어.plicitl y 는 점근팽창에 표시됩니다.
행켈 함수는 각각 원통파 방정식의 외향 및 내향 전파 원통파 용액을 표현하기 위해 사용된다(또는 주파수 에 대한 부호 규칙 에 따라 그 반대).
이전 관계를 사용하면 다음과 같이 표현할 수 있습니다.
H α ( 1 ) ( x ) = J − α ( x ) − e − α π i J α ( x ) i 죄 α π , H α ( 2 ) ( x ) = J − α ( x ) − e α π i J α ( x ) − i 죄 α π . 디스플레이 스타일 H_{\alpha }^{(1)(x)&=frac {J_{-\alpha }(x)-e^{-\alpha \pi i}J_{\alpha }(x)}{i\sin \alpha \pi },\H_{\alpha }^{(2)(x)&frAC {\alpha} \end { aligned}}
α가 정수일 경우 한계를 계산해야 합니다. α가 정수인지 [18] 관계없이 다음 관계가 유효합니다.
H − α ( 1 ) ( x ) = e α π i H α ( 1 ) ( x ) , H − α ( 2 ) ( x ) = e − α π i H α ( 2 ) ( x ) . 디스플레이 스타일 H_{-\alpha }^{(1)(x)&=e^{\alpha \pii}H_{{(1)}(x),\H_{-\alpha }^{(2)(x)&=e^{-\alpha \piiii}H_{(2)(x). \end { aligned}}
특히, m이 음이 아닌 정수인 α 경우
J − ( m + 1 2 ) ( x ) = ( − 1 ) m + 1 Y m + 1 2 ( x ) , Y − ( m + 1 2 ) ( x ) = ( − 1 ) m J m + 1 2 ( x ) . {{displaystyle {begin{aligned}J_{-(m+{\frac {1}{2}}}}(x),\Y_{-(m+{\frac {1}{2}}},\Y_{-(x)&{{1}{{{2}}}}) \end { aligned}}
이들은 구형 베셀 함수를 개발하는 데 유용합니다(아래 참조).
행켈 함수는 Re(x ) > [19] 0에 대해 다음과 같은 적분 표현을 허용합니다.
H α ( 1 ) ( x ) = 1 π i ∫ − ∞ + ∞ + π i e x 쌍곡선 정현. t − α t d t , H α ( 2 ) ( x ) = − 1 π i ∫ − ∞ + ∞ − π i e x 쌍곡선 정현. t − α t d t , 디스플레이 스타일 H_{\alpha }^{(1)(x)&=hargfrac {1}{\pi i}\int _{-\infty}^{+\infty +\pi i}e^{x\sinh t-\alpha t},dt,\H_{\alpha }^{(2)(x)={\pi i}}} {-\fi i} 여기서 적분 한계는 음의 실제 축을 따라 -125 ~ 0, 가상 축을 따라 0 ~ ±125i , 그리고 [16] 125 µi 등고선 을 따라 적분을 나타낸다.
Iα Kα 베셀 함수는 복잡한 인수 x 에도 유효하며, 중요한 특수한 경우는 순전히 상상의 인수이다. 이 경우, 베셀 방정식에 대한 해는 제1종과 제2종의 수정 된 베셀 함수(또는 때때로 쌍곡선 베셀 함수)라고 불리며 다음과 같이 정의된다[20]
I α ( x ) = i − α J α ( i x ) = ∑ m = 0 ∞ 1 m ! Γ ( m + α + 1 ) ( x 2 ) 2 m + α , K α ( x ) = π 2 I − α ( x ) − I α ( x ) 죄 α π , 디스플레이 스타일 I_{\alpha }(x)&=i^{-\alpha}J_{{\alpha}(ix)=\sum _{m=0}^{\infty}{\frac {1}{m!\Gamma(m+\alpha +1)}}\lefti\frac\frac {x}{x}{2+\k}, α가 정수가 아닌 경우 , α가 정수인 경우 한계값이 사용됩니다. 이들은 실제 인수와 양의 인수 x에 대해 실제 값으로 선택됩니다. 따라서 I(x ) 의α 시계열 팽창은 J(x ) 의α 시계열 팽창과 유사하지만 교대 요인 (-1)m 은 없습니다.
Kα (\ displaystyle K_{\alpha
K α ( x ) = { π 2 i α + 1 H α ( 1 ) ( i x ) − π < > arg x ≤ π 2 π 2 ( − i ) α + 1 H α ( 2 ) ( − i x ) − π 2 < > arg x ≤ π {\displaystyle K_{\alpha }(x)=case {\frac {pi } {2} i^{\alpha }H_{\alpha }^{(1)(ix)&-\pi <\frac x\pi }{2-i }\{\frac {\frac {pi } {2-} {\fi} {{{{{{{{pi} {\alpha} {pi}
이 α z displaystyle J_{\alpha 2}(z) } Y α ( z ) displaystyle Y_{\alpha 2}(z 다음
J α 2 ( x ) + Y α 2 ( x ) = 8 π 2 ∫ 0 ∞ 아늑하다 ( 2 α t ) K 0 ( 2 x 쌍곡선 정현. t ) d t , \displaystyle J_{\alpha }^2}(x)+ Y_{\alpha }^{2}(x)=hargfrac {8}{\pi ^{2}}\int _{0}^{\infty }\cosh(2\alpha t)K_{0}(2x\sinh t),dt,}
조건 Re (x)> 0 이 충족된 경우.라는 것도 알 수 있다.
J α 2 ( x ) + Y α 2 ( x ) = 8 왜냐하면 ( α π ) π 2 ∫ 0 ∞ K 2 α ( 2 x 쌍곡선 정현. t ) d t , \displaystyle J_{\alpha }^2}(x)+ Y_{\alpha }^{2}(x)=hargfrac {8\cos(\alpha \pi)}{\int _{0}^{\infty}}K_{2\alpha }(2x\sinh t),d,}
Re(α) < 1 / 2 Re(x) 0 0인 경우 에만 해당되지만 x = [21] 0인 경우 에는 해당되지 않습니다.
첫 번째와 두 번째 베셀 함수를 수정된 베셀 함수로 표현할 수 있습니다(-π < arg π [22] 2일
J α ( i z ) = e α π i 2 I α ( z ) , Y α ( i z ) = e ( α + 1 ) π i 2 I α ( z ) − 2 π e − α π i 2 K α ( z ) . 디스플레이 스타일 J_{\alpha }(iz) &=e^{\frac{alpha\pii}{2}} I_{\alpha }(z),\Y_{\alpha }(iz) &=e^{\frac{(\alpha +1)\pi i}{2}} I_{\alpha }(z)-{\frac {2}{\pi }}e^{-{\frac {\alpha \pi i}{2}}K_{\alpha }(z) \end { aligned}}
Iα (x )α K(x ) 는 수정된 베셀 [23] 에 대한 두 개의 선형 독립 해이다.
x 2 d 2 y d x 2 + x d y d x − ( x 2 + α 2 ) y = 0. {\displaystyle x^{2}{\frac {d^2}y}+xfrac {dy}{flac}-\left(x^{2}+\alpha^{2}\right)y=0. }
실제 인수의 함수로 진동하는 일반적인 베셀 함수와 달리 I 와α α K는 각각 기하급수적으로 성장 하고 붕괴 하는 함수이다. 일반적인 베셀 함수α J와 마찬가지로 함수α I는 α > 0 에 대해 0 에 대해 0으로 가고 α = 0 에 대해서 0 에서 유한하다. 이와 유사하게, K 는α K에 대해0 로그형이고, [24] 그렇지 2Ω α x ) α
α = 0, 1, 2 , 3 에 대해 종류 α I ( x)의 수정된 베셀 함수 α = 0, 1, 2, 3 에 대해 종류 α K(x ) 의 수정된 베셀 함수
변경된 Bessel 함수의 2개의 정수식은 다음과 같습니다(Re (x)> [25] 0 의 경우).
I α ( x ) = 1 π ∫ 0 π e x 왜냐하면 θ 왜냐하면 α θ d θ − 죄 α π π ∫ 0 ∞ e − x 아늑하다 t − α t d t , K α ( x ) = ∫ 0 ∞ e − x 아늑하다 t 아늑하다 α t d t . 디스플레이 스타일 I_{\alpha }(x)&=nt frac {1}{\pi }}\int _{0}^{\pi }e^{x\cos \theta }\cos \alpha \theta \,d\theta - {\frac \sin \pi }{\pi }{\flac }{\cos - {\cos }{\cos }\cos - t} \end { aligned}}
베셀 함수는 2차 함수의 거듭제곱의 푸리에 변환으로 설명할 수 있다. 예를 들어 다음과 같습니다.
2 K 0 ( ω ) = ∫ − ∞ ∞ e i ω t t 2 + 1 d t . {\displaystyle 2,K_{0}(\obega)=\int _{-\infty }^{\infty}{\frac {e^{i\obega t}}{\fracrt {t^{2}+1}},dt. }
이는 K에 대해 0 이는 복합 평면의 첫 번째 사분면에 닫힌 곡선을 통합함으로써 이루어집니다.
수정된 베셀 함수 1/3 K 2/3 K는 빠르게 수렴하는[26]
K 1 3 ( ξ ) = 3 ∫ 0 ∞ exp ( − ξ ( 1 + 4 x 2 3 ) 1 + x 2 3 ) d x , K 2 3 ( ξ ) = 1 3 ∫ 0 ∞ 3 + 2 x 2 1 + x 2 3 exp ( − ξ ( 1 + 4 x 2 3 ) 1 + x 2 3 ) d x . ({displaystyle {begin{aligned}K_{1}{3}}&=sqrt {3}}{0}^{\infty}\exp \left \xi \left(1+{\frac {4x^2}}{{3}}\right) {\sqrt {1+{\frac {1+{\frac{}{}{}}{{}}}}}}}}{{{{d}}}}}}}}}}}}}}}}}}}}}}}{\right}}} }}{\caprt {1+{\frac {x^{2}}{3}}}\exp \left\xi \left(1+{4x^{2}}}{3}}}\right){\caprt {1+{x^{2}}{3}}}}}{\right}}}}}}\capraprt {\\caph},\ended}}}},caprate\left\left\left\left\frac\left{xp\left {xp\left}}}}
수정된 베셀 함수 K 2 ) = - 2 ξ displaystyle K_{\frac {1}{2}\ xi ^{-1/2}\expa\ }
두 번째 종류의 수정된 베셀 함수도 다음 과 같은 이름으로 호출되었습니다(현재는 거의 없음).
jn yn n = 0, 1 , 2 에 대한 함수n (x ) n = 0, 1 , 2 에 대한 종류 n 구면 베셀 함수 y(x ) 변수의 분리에 의해 구좌표에서 헬름홀츠 방정식을 풀 때, 방사 방정식은 다음과 같은 형태를 가진다.
x 2 d 2 y d x 2 + 2 x d y d x + ( x 2 − n ( n + 1 ) ) y = 0. \displaystyle x^{2}{\frac {d^{2}y}+2xfrac {dy}{flac}+\left(x^{2}-n(n+1)\right)y=0. }
이 방정식에 대한 두 선형 독립 해는 구면 베셀 함수n j 와n y라고 불리며, 일반적인 베셀 함수n J 와n Y와[28]
j n ( x ) = π 2 x J n + 1 2 ( x ) , y n ( x ) = π 2 x Y n + 1 2 ( x ) = ( − 1 ) n + 1 π 2 x J − n − 1 2 ( x ) . {\displaystyle {displaystyle}j_{n}(x)&=j_{n+{1}{2}}(x),\y_{n}(x)&=syslogrt {pi }{2x} Y_{n+}{x1}{x}{displaystyle} \end { aligned}}
또한n y는 n 또는 θ n 표시 되며n , 일부 저자는 이러한 함수를 구면 노이만 함수 라고 부른다.
일반적인 베셀 함수와의 관계에서 직접 확인할 수 있는 것은 다음과 같습니다.
j n ( x ) = ( − 1 ) n y − n − 1 ( x ) y n ( x ) = ( − 1 ) n + 1 j − n − 1 ( x ) {{displaystyle {displaystyle}j_{n}(x)&=n1}y_{-n1}(x)&=ndisplay1)^{n+1}j_{-n-1}(x)\end{naligned}}} 구형 베셀 함수는 (Rayleigh의 공식) [29]
j n ( x ) = ( − x ) n ( 1 x d d x ) n 죄 x x , y n ( x ) = − ( − x ) n ( 1 x d d x ) n 왜냐하면 x x . {{displaystyle {d}j_{n}(x)&=displayx)^{n}\left\frac {1}{x}{\frac {d}{frac}\right} ^{n}{\frac {sin x}{x}},\y_{n}(x)&=-(-x)^{n}\leftfrac {1}{x}{\frac {d}{x}}}\오른쪽) ^{n}{\frac{cos x}{x}}. \end { aligned}}
0 구면 베셀 함수 0 (x ) 는 (비정규화된) 동기 함수라고도 합니다. 처음 몇 개의 구형 베셀 함수는 다음과 같습니다.[30]
j 0 ( x ) = 죄 x x . j 1 ( x ) = 죄 x x 2 − 왜냐하면 x x , j 2 ( x ) = ( 3 x 2 − 1 ) 죄 x x − 3 왜냐하면 x x 2 , j 3 ( x ) = ( 15 x 3 − 6 x ) 죄 x x − ( 15 x 2 − 1 ) 왜냐하면 x x {\displaystyle\displaystyle}j_{0}(x)&=snaphfrac {sin x}{x}. \\j_{1}(x)&=frac {sin x}{x^{2}}-{\frac {cos x}{x},\j_{2}(x)&=\frac\frac {3}{x}-1\right}{\frac {x}-{x2}-{\frac {x}{x}} 그리고[31] y 0 ( x ) = − j − 1 ( x ) = − 왜냐하면 x x , y 1 ( x ) = j − 2 ( x ) = − 왜냐하면 x x 2 − 죄 x x , y 2 ( x ) = − j − 3 ( x ) = ( − 3 x 2 + 1 ) 왜냐하면 x x − 3 죄 x x 2 , y 3 ( x ) = j − 4 ( x ) = ( − 15 x 3 + 6 x ) 왜냐하면 x x − ( 15 x 2 − 1 ) 죄 x x . eft({\frac{15}{ x^{2}}-1\right {\frac {sin x}{x}}. \end { aligned}}
생성함수 구형 베셀 함수는 생성 함수를 가집니다[32]
1 z 왜냐하면 ( z 2 − 2 z t ) = ∑ n = 0 ∞ t n n ! j n − 1 ( z ) , 1 z 죄 ( z 2 − 2 z t ) = ∑ n = 0 ∞ t n n ! y n − 1 ( z ) . {\displaystyle {\frac {1}{z}}\cos \leftrt {z^{2}-2zt}\right}&=\sum _{n=0}^{\infty}{\frac {t^{n}}{n}}\frac {n! }j_{n-1}(z),\{\frac {1}{z}}\sin \lefthrt {z^{2}-2zt}}\right)&=\sum _{n=0}^{\infty}{\frac {t^{n}}{n}}{n! }}y_{n-1}(z) \end { aligned}}
미분 관계 다음에서 f 는n n = 0, ±1, ±2, [33] 대한 yn , h (1) n h (2) n 하나 이다n .
( 1 z d d z ) m ( z n + 1 f n ( z ) ) = z n − m + 1 f n − m ( z ) , ( 1 z d d z ) m ( z − n f n ( z ) ) = ( − 1 ) m z − n − m f n + m ( z ) . (\displaystyle\leftfrac {1}{z}}{\frac {d}{dz}}\오른쪽) ^{m}\left(z^{n+1}f_{n}(z)\right)&=z^{n-m+1}f_{n-m}(z),\lefts\frac\frac{1}{z}{\frac {d}{dz}}}\right) ^{m}\left(z^{-n}f_{n}(z)\right)&=param1)^{m}z^{-n-m}f_{n+m}(z). \end { aligned}}
h (1) n h (2) n 행켈 함수에는 다음과 같은 구형 유사체도 있습니다.
h n ( 1 ) ( x ) = j n ( x ) + i y n ( x ) , h n ( 2 ) ( x ) = j n ( x ) − i y n ( x ) . {\displaystyle {signed}h_{n}^{(1)(x)&=j_{n}(x)+iy_{n}(x)^{(2)}(x)&=j_{n}(x)-iy_{n}(x) \end { aligned}}
사실, 표준 삼각함수 측면에서 반정수 차수의 베셀 함수에 대한 단순한 폐쇄형 표현식이 있으며, 따라서 구면 베셀 함수에 대한 표현식이 있다. 특히 음수가 아닌 정수 n의 경우:
h n ( 1 ) ( x ) = ( − i ) n + 1 e i x x ∑ m = 0 n i m m ! ( 2 x ) m ( n + m ) ! ( n − m ) ! , {\displaystyle h_{n}^{n}{x}{\frac {e^{ix}}{x}{n}{\frac {i^{m}}{m!,(2x)^{m}}}{\frac {n+m}}}{\frac {n+m}}!,\frac {(n+m)}! }{(n-m)! }},}
h (2) n 실제 x의 경우).예 0 들어 j(x ) = sin / x 0 (x ) = -cos / x
구형 행켈 함수는 예를 들어 전자장의 다극 확장 과 같은 구형 파장의 전파와 관련 된 문제에서 나타난다.
Sn Cn ζn n 리카티-베셀 함수는 구형 베셀 함수와 약간 다를 뿐이다.
S n ( x ) = x j n ( x ) = π x 2 J n + 1 2 ( x ) C n ( x ) = − x y n ( x ) = − π x 2 Y n + 1 2 ( x ) ξ n ( x ) = x h n ( 1 ) ( x ) = π x 2 H n + 1 2 ( 1 ) ( x ) = S n ( x ) − i C n ( x ) ζ n ( x ) = x h n ( 2 ) ( x ) = π x 2 H n + 1 2 ( 2 ) ( x ) = S n ( x ) + i C n ( x ) 디스플레이 스타일 S_{n}(x)&=xj_{n}(x)=sqrt {frac {pi x}{2}}J_{n+{1}{2}}(x)\ \C_{n}(x)&=-xy_{n}(x)=-{\sqrt {frac {1}{2}}(x)\xi _{n}(x)&=xh_{n}^(1)(x)={\sqrt} Y_{n+{frac {1}(x)
그들은 미분방정식을 만족시킨다.
x 2 d 2 y d x 2 + ( x 2 − n ( n + 1 ) ) y = 0. {\displaystyle x^{2}{d^{2}y}+\left(x^{2}-n(n+1)\right)y=0. }
예를 들어, 이러한 미분 방정식은 슈뢰딩거 방정식 의 반경 성분을 가상의 원통형 무한 전위 [34] 양자 역학에서 나타난다 . 이 미분 방정식과 리카티-베셀 해법은 또한 Mie(1908)가 최초로 발표한 해법 이후 Mie 산란으로 알려진 구에 의한 전자파의 산란 문제에서도 발생한다. 최근 개발 및 참고 자료는 Du(2004)[35]
Debye (1909)에 이어 S, Cn 대신n 표기법n ,, is 가n 사용되는 경우가 있습니다.
점근형식 베셀 함수는 다음과 같은 점근 형태를 가집니다. 작은 인수 0 < z δα 1 [3] 다음 을 구한다.
J α ( z ) ∼ 1 Γ ( α + 1 ) ( z 2 ) α . {\displaystyle J_{\alpha }(z)\sim {\Gamma(\alpha +1)}}\left({\frac {z}{2}}\right)^{\alpha}}}}.
α가 음의 정수일 때 , 우리는
J α ( z ) ∼ ( − 1 ) α ( − α ) ! ( 2 z ) α . {\displaystyle J_{\alpha }(z)\sim {frac {(-1)^{\alpha }}{(-\alpha)! }}\frac {2}{z}}\right)^{\alpha}.}.
두 번째 종류의 베셀 함수의 경우 세 가지 사례가 있습니다.
Y α ( z ) ∼ { 2 π ( 인 ( z 2 ) + γ ) 한다면 α = 0 − Γ ( α ) π ( 2 z ) α + 1 Γ ( α + 1 ) ( z 2 ) α 요람 ( α π ) 한다면 α 비양정수가 아니다(단, 1항이항이 지배한다). α 상상의 문제) , − ( − 1 ) α Γ ( − α ) π ( z 2 ) α 한다면 α 음의 정수입니다. {\displaystyle Y_{\alpha}(z)\sim{\begin{경우}{\dfrac{2}{\pi}}\left(\ln \left({\dfrac{z}{2}}\right)+\gamma \right)&{\text{만약}}\alpha =0\\-{\dfrac{\Gamma)}{\pi}}\left({\dfrac{2}{z}}\right)^{\alpha}+{\dfrac{1}{\Gamma(\alpha +1)}}\left({\dfrac{z}{2}}\right)^ᆹ\cot(\alpha \pi)&,{\text{만약}}\alpha{\text{ 아니다.n-positi ve integer ( } \ alpha { \ text { } } \ \ \ dfrac { ( - 1 )^{ \ alpha } \ Gamma ( \ alpha ) } { \ pi } } \ left ( \ dfrac { z } { } { \ right )^{ \ text { if } } \ alpha { negative } } } \ alpha { } } } } } \ \ \ \ \ \ \ } {}}}}}}}} {\ {\}}}}}}}}}}}} 여기서 θ 는 오일러-마셰로니 상수 (0.5772...)이다.
큰 실수 인수 α2 - 1 4 반정수인 경우는 제외 ). 왜냐하면 그들은 무한대까지 0을 가지기 때문에, 어떤 점근적 팽창에 의해서도 정확히 일치해야 한다. 단, 주어진 arg 순서항 [36]
J α ( z ) = 2 π z ( 왜냐하면 ( z − α π 2 − π 4 ) + e 나는 ( z ) O ( z − 1 ) ) 위해서 arg z < > π , Y α ( z ) = 2 π z ( 죄 ( z − α π 2 − π 4 ) + e 나는 ( z ) O ( z − 1 ) ) 위해서 arg z < > π . 디스플레이 스타일 J_ᆭ(z)&, ={\sqrt{\frac{2}{z\pi}}}\left(\cos \left(z-{\frac{\alpha \pi}{2}}-{\frac{\pi}{4}}\right)+e^{\left \operatorname{ 난}(z)\right}\mathrm{O}\left(z^{-1}\right)\right)&&{\text{에}}\left \argz\right<>\pi ,\\Y_ᆳ(z)&, ={\sqrt{\frac{2}{z\pi}}}\left(\sin \left(}z-{\frac{\alpha)}{2}-{\frac{\pi}.{4}}\right)+e^{\lef t \operatorname {Im}(z)\right }\mathrm {O}\left(z ^{-1}\right)&{\text{for }}\left \arg z\right <\pi .\end{aligned}}})&{\text{\text{ }
(α = 1 /2 경우 이러한 방정식이 참일지라도 복소 z에 대해 더 나은 근사치를 사용할 수 있습니다. 예를 들어, z가 음의 실선 근처에 있을 때 J(z ) 는 다음 0 같이 근사됩니다.
J 0 ( z ) ≈ − 2 π z 왜냐하면 ( z + π 4 ) ({displaystyle J_{0}(z)\약 {sqrt {-2}{\pi z}}\cos \left(z+{\frac {\pi }{4}}\right)) 에 의해서 J 0 ( z ) ≈ 2 π z 왜냐하면 ( z − π 4 ) . {\displaystyle J_{0}(z)\약 {\frac {2}{\pi z}}\cos \left(z-{\frac {pi }{4}}\오른쪽). }
행켈 함수의 점근 형식은 다음과 같습니다.
H α ( 1 ) ( z ) ∼ 2 π z e i ( z − α π 2 − π 4 ) 위해서 − π < > arg z < > 2 π , H α ( 2 ) ( z ) ∼ 2 π z e − i ( z − α π 2 − π 4 ) 위해서 − 2 π < > arg z < > π . 디스플레이 스타일 H_{\alpha }^{(1)(z)&\sim {sqrt {2}{\pi z}}e^{i\left(z-{\frac {alpha \pi }{2}}-{\frac {pi }{4}}\right} }&{\text{for }-\pi z<2\pi,\H_{\alpha}^{(2)}(z)&\sim {{frac {2}{pi z}}e^{-i-{\frac \pi }{-}{\flac }{\pi } {\fright}} }&{\text{ for }-2\pi <\pi .\end { aligned}}
이러한 값은 H im π ze)와(2) α H im π ze)에서(1) α (1) α (z ) 와(2) α (z ) [37] arg 다른 값으로 확장할 수 있습니다.
흥미로운 점은 첫 번째 종류의 베셀 함수는 두 항켈 함수의 평균이지만, z가 음수일 때 J (z ) 는α 이 두 점근 형태의 평균에 점근적이지 않다는 것이다(사용된 아르그 그러나 행켈 함수에 대한 점근 형식을 사용하면 z가 (정의 실수를 갖는 제곱근을 사용하여) 일정한 위상각 arg 한 복소(비실제) z 에 대한 제1종 및 제2종의 베셀 함수에 대한 점근 형식을 쓸 수 있다.
J α ( z ) ∼ 1 2 π z e i ( z − α π 2 − π 4 ) 위해서 − π < > arg z < > 0 , J α ( z ) ∼ 1 2 π z e − i ( z − α π 2 − π 4 ) 위해서 0 < > arg z < > π , Y α ( z ) ∼ − i 1 2 π z e i ( z − α π 2 − π 4 ) 위해서 − π < > arg z < > 0 , Y α ( z ) ∼ i 1 2 π z e − i ( z − α π 2 − π 4 ) 위해서 0 < > arg z < > π . 디스플레이 스타일 J_{\alpha }(z)&\sim {frac {1}{\sqrt {2\pi z}}}e^{i\left(z-{\frac {alpha \pi }{2}}-{\frac {pi }{4}}\right) }&{\text{ for }}-\pi <\arg z<0,\J_{\alpha }(z)&\sim {\sqrt {2\pi z}}}e^{-i\left(z-{\frac \pi }{\frci }{4}}}}-{\}}}}}-{\sim {\fracpi}}}}}}}}}}}}} }&{\text{for}}0<\arg z<\pi,\Y_{\alpha}(z)&\sim -i{\pi z}{\sqrt {2\pi z}}}e^{i\left(z-{\frac \pi }{2}-{\fracpi }}}}}{\}}}}}}}{\}}}}}}}{\}}}}}}\right }&{\text{ for }}-\pi <\text z <0,\\\ Y_{\alpha }(z)&\sim i{\sqrt {2\pi z}}}e^{-i\left(z-{\frac {alpha \pi }{2}}-{\frac {pi }{4}}\right}) }&{\text{}}0<\text z<\pi.\end{aligned}}}
수정된 베셀 함수의 경우,[38] [39] 행켈은 점근적(큰 인수) 확장 도 개발했습니다.
I α ( z ) ∼ e z 2 π z ( 1 − 4 α 2 − 1 8 z + ( 4 α 2 − 1 ) ( 4 α 2 − 9 ) 2 ! ( 8 z ) 2 − ( 4 α 2 − 1 ) ( 4 α 2 − 9 ) ( 4 α 2 − 25 ) 3 ! ( 8 z ) 3 + ⋯ ) 위해서 arg z < > π 2 , K α ( z ) ∼ π 2 z e − z ( 1 + 4 α 2 − 1 8 z + ( 4 α 2 − 1 ) ( 4 α 2 − 9 ) 2 ! ( 8 z ) 2 + ( 4 α 2 − 1 ) ( 4 α 2 − 9 ) ( 4 α 2 − 25 ) 3 ! ( 8 z ) 3 + ⋯ ) 위해서 arg z < > 3 π 2 . 디스플레이 스타일 I_ᆰ(z)&.({\frac{e^{z}}{\sqrt{2\pi z}}}\left(1-{\frac{4\alpha ^{2}-1}{8z}}와{\frac{\left(4\alpha ^{2}-1\right)\left(4\alpha ^{2}-9\right)}{2!(8z)^{2}}}-{\frac{\left(4\alpha ^{2}-1\right)\left(4\alpha ^{2}-9\right)\left(4\alpha ^{2}-25\right)}{3!(8z)^{3}}}+\cdots \right)&&{\text{에}}\left \argz\right<>{\frac{\pi}{2}.},\\K_{\alpha} (z)&\sim {\frac {\pi }{2z} e^{-z}\left(1+{\frac {4\alpha ^{2}-1}{8z}}+{\frac {left(4\alpha ^{2}-1\right)\left(4\alpha ^{2}-9\right)}{2}{8z}{2}}{2+^2}}{2}}{2}{2}}}{-z}{2}}}}{-z}}}}}}}{2}}{ \end { aligned}}
점근 형태도 있습니다(큰 실제 z의 경우 [40]
I α ( z ) = 1 2 π z 1 + α 2 z 2 4 exp ( − α arsinh ( α z ) + z 1 + α 2 z 2 ) ( 1 + O ( 1 z 1 + α 2 z 2 ) ) . 디스플레이 스타일 I_{\alpha }(z)=parcfrac {1}{\parcrt {2\pi z}}{\parcrt[{4}}{1+{\frac {alpha ^{2}}}}}}\exp \operatorname {arsinh} \left\frac {arcrcrcrcrcrcrt {2}{{{z}{z}{{z}}}}{\p}{\parcrt}{\p}{\p}}{\p}{ \end { aligned}}
α = 1/2일 때
I 1 2 ( z ) = 2 π z 신 ( z ) ∼ e z 2 π z 위해서 arg z < > π 2 , K 1 2 ( z ) = π 2 z e − z . 디스플레이 스타일 I_{\frac {1}{2}(z)&=sinh(z)\sim {frac {e^{z}}{\fracrt {2\pi z}}&{\text{for }}\left z\right {\tfrac {pi z}}&{\frac {\frc}\frac {\f}\fr},\frac {\frac}, {\frac}, \end { aligned}}
작은 인수 0 < z ≪ α α + 1의 경우, 다음과 같이 합니다.
I α ( z ) ∼ 1 Γ ( α + 1 ) ( z 2 ) α , K α ( z ) ∼ { − 인 ( z 2 ) − γ 한다면 α = 0 Γ ( α ) 2 ( 2 z ) α 한다면 α > 0 디스플레이 스타일 I_{\alpha }(z)&\sim {frac {1}{\Gamma(\alpha +1)}}\left(왼쪽){\alpha}{\alpha}(z)&\sim {case}-\left\dfracz}{2}\text}\{\text}\lan }
특성. 정수 차수α n J 는n 종종 생성 함수를 위해 로랑 급수를 통해 정의됩니다.
e ( x 2 ) ( t − 1 t ) = ∑ n = − ∞ ∞ J n ( x ) t n {\displaystyle e^{\displaystyle\frac {x}{x}}\right(t-{\frac {1}{t}\right)}=\sum _{n=-\infty}{\infty}}J_{n}(x)t^{n}}}}} 1843년 P. A. Hansen에 의해 사용된 접근법(이 는 등고선 적분 또는 다른 방법에 의해 비정수 순서로 일반화될 수 있다.)
베셀 함수(Kapteyn 시리즈 )를 사용한 직렬 확장:
1 1 − z = 1 + 2 ∑ n = 1 ∞ J n ( n z ) . {{displaystyle {1}{1-z}}=1+2\sum _{n=1}^{\infty }J_{n}(nz). } 정수 차수의 또 다른 중요한 관계는 야코비- 분노
e i z 왜냐하면 ϕ = ∑ n = − ∞ ∞ i n J n ( z ) e i n ϕ \displaystyle e^{iz\cos \phi }=\sum _{n=-\infty }^{\infty }i^{n}J_{n}(z)e^{in\phi}}} 그리고. e ± i z 죄 ϕ = J 0 ( z ) + 2 ∑ n = 1 ∞ J 2 n ( z ) 왜냐하면 ( 2 n ϕ ) ± 2 i ∑ n = 0 ∞ J 2 n + 1 ( z ) 죄 ( ( 2 n + 1 ) ϕ ) {\displaystyle e^{\pm iz\phi }=J_{0}(z)+2\sum_{2n}(z)\cos(2n\phi)\pm 2i\sum _{n=0}{\infty }J_{2n+1(sin)(sin) 평면파 를 원통파의 합 으로 확장하거나 톤 변조 FM 신호의 푸리에 시리즈 를 찾는 데 사용됩니다.
보다 일반적으로는 일련의
f ( z ) = a 0 ν J ν ( z ) + 2 ⋅ ∑ k = 1 ∞ a k ν J ν + k ( z ) {\displaystyle f(z)=a_{0}^{\nu }J_{\nu }+2\cdot \sum _{k=1}^{\infty }a_{\nu }J_{\nu +k}(z)} F 의 노이만 확장이라고 합니다.θ = 0에 대한 계수는 명시적 형식을 갖습니다. a k 0 = 1 2 π i ∫ z = c f ( z ) O k ( z ) d z {\displaystyle a_{k}{0}=snapfrac {1}{2\pi i}}\int _{z =c}f(z) O_{k}(z),dz} 여기 서k O는 노이만의 다항식 이다.[41]
선택한 함수는 특수 표현을 허용합니다.
f ( z ) = ∑ k = 0 ∞ a k ν J ν + 2 k ( z ) {\displaystyle f(z)=\sum _{k=0}^{\infty }a_{\nu }{\nu +2k}(z)} 와 함께 a k ν = 2 ( ν + 2 k ) ∫ 0 ∞ f ( z ) J ν + 2 k ( z ) z d z {\displaystyle a_{k}^{\nu }=2(\nu +2k)\int _{0}^{\infty }f(z){\frac {J_{\nu +2k}(z)}{z},dz} 직교 관계에 의해 ∫ 0 ∞ J α ( z ) J β ( z ) d z z = 2 π 죄 ( π 2 ( α − β ) ) α 2 − β 2 \displaystyle \int _{0}^{\infty}J_{\alpha }(z) J_{\beta }(z){\frac {dz}{\pi }=frac {2}{\frac {\pi }}{\frac {sin \left pi }{2}-\flac ^{2}}}}{\alpha -\frac ^{2}}}}}
보다 일반적으로 f가 다음과 같은 성질의 원점 근처에 분기점을 갖는 경우
f ( z ) = ∑ k = 0 a k J ν + k ( z ) {\displaystyle f(z)=\sum _{k=0}a_{k}J_{\nu +k}(z)} 그리고나서 L { ∑ k = 0 a k J ν + k } ( s ) = 1 1 + s 2 ∑ k = 0 a k ( s + 1 + s 2 ) ν + k {\displaystyle {\mathcal {L}\left\{k=0}a_{k}J_{\nu +k}\right\}=secfrac {1}{\displaystyle {1+s^{2} }}}}}\sum _{k=0}{\frac {a_{k}}{\left(s+{\superrt {1+s^{2}) }}\오른쪽)^{\nu +k}}}} 또는 ∑ k = 0 a k ξ ν + k = 1 + ξ 2 2 ξ L { f } ( 1 − ξ 2 2 ξ ) {\displaystyle \sum _{k=0}a_{k}\xi ^{\nu +k}={2\xi ^{2}}{\mathcal {L}\{f\}\left({\frac {1-\xi ^2}}{2\xi }}}}\right) 여기 f } displaystyle mathcal L}} f [42] f 의 라플라스 변환입니다.
베셀 함수를 정의하는 또 다른 방법은 포아송 표현 공식과 Mehler-Sonine 공식입니다.
J ν ( z ) = ( z 2 ) ν Γ ( ν + 1 2 ) π ∫ − 1 1 e i z s ( 1 − s 2 ) ν − 1 2 d s = 2 ( z 2 ) ν ⋅ π ⋅ Γ ( 1 2 − ν ) ∫ 1 ∞ 죄 z u ( u 2 − 1 ) ν + 1 2 d u 디스플레이 스타일 J_ᆯ(z)&, ={\frac{\left({\frac{z}{2}}\right)^{\nu}}{\Gamma \left(\nu+{\frac{1}{2}}\right){\sqrt{\pi}}}}\int _ᆲ^ᆳe^ᆴ\left(1-s^{2}\right)^{\nu-{\frac{1}{2}}}\,ds\\[5px]&, ={\frac{2}{{\left({\frac{z}{2}}\right)}^{\nu}\cdot{\sqrt{\pi}}\cdot \Gamma \left({\frac{1}{2}}-\nu\right)}}\int _{1}^{\infty}{\frac{\sin zu}{\lef.t(u^{2}- 1\right)^{\nu +{\frac {1}{2}}}}}}}, du\end {aligned}}} 여기서 > -1/ 2 및 z c [43] 이 공식은 푸리에 변환을 사용 할 때 특히 유용합니다.
베셀 방정식은 x 로 나누면 에르미트 방정식(자기접점)이 되므로, 해는 적절한 경계 조건에 대한 직교 관계를 만족해야 합니다. 특히 다음과 같습니다.
∫ 0 1 x J α ( x u α , m ) J α ( x u α , n ) d x = δ m , n 2 [ J α + 1 ( u α , m ) ] 2 = δ m , n 2 [ J α ′ ( u α , m ) ] 2 \displaystyle \int _{0}^{\alpha}\left(xu_{\alpha,m}\오른쪽) J_{\alpha }\left(param_{\alpha,n}\오른쪽), param=param frac {{m,n}{2}}\left[ J_{\alpha +1}\left(u_{\alpha,m}\right)^{2}=parc frac {{m,n}{2}}\left[ J_{\alpha }'\left(u_{\alpha,m}\right)\right]^{2}} 여기 α > -1 , θ m ,n α ,m 크로네커 델타, u는 J(x ) 의α m번째 0이다.그런 다음 이 직교 관계를 사용하여 푸리에-베셀 계열의 계수를 추출할 수 있으며, 여기서 함수는 고정 α 및 가변 m에 대한 함수α (x α ,m u)에 기초하여 확장된다.
구면 베셀 함수에 대한 유사한 관계는 즉시 다음과 같다.
∫ 0 1 x 2 j α ( x u α , m ) j α ( x u α , n ) d x = δ m , n 2 [ j α + 1 ( u α , m ) ] 2 \displaystyle \int _{0}^{\alpha }j_{\alpha }\left (\alpha,m}\right)j_{\alpha }\left (parama_{\alpha,n}\right), paramp =parcfrac {{{{{{m,n}{\alpha}{{{\alpha}{\left}\alpha}{\alpha}{\left}{\alpha}{{\left}{{{{{
작은 매개변수 θ 에 의존하는 x 의 박스카 함수를 다음과 같이 정의하는 경우:
f ε ( x ) = ε 직교하다 ( x − 1 ε ) {\displaystyle f_{\varepsilon }(x)=\varepsilon \operatorname {rect}\frac {x-1}{\varepsilon }}\right} (여기 서 rect는 직사각형 함수이다) 그 다음 (임의 순서α > -1/2 gε (k )행켈 변환은 임의 의 k에 대해 θ 가 0에 가까워짐에 따라 J(k ) 에α 접근한다. 반대로, g (ε 행켈 변환(같은 차수)은ε f(x )이다. ∫ 0 ∞ k J α ( k x ) g ε ( k ) d k = f ε ( x ) \displaystyle \int _{0}^{\infty }kJ_{\alpha }(kx)g_{\varepsilon }(k),dk=f_{\varepsilon }(x)} 1을 제외하고 모든 것이 0입니다. θ 가 0에 가까워지면 우측은 θ (x - 1 )에 가까워집니다.여기서 θ 는 Dirac 델타 함수입니다.이것은 (분포적 인 의미에서) 다음 제한을 허용한다. ∫ 0 ∞ k J α ( k x ) J α ( k ) d k = δ ( x − 1 ) \displaystyle \int _{0}^{\infty}kJ_{\alpha}(kx) J_{\alpha }(k),dk=\context (x-1)}
변수를 변경하면 폐쇄 [44]
∫ 0 ∞ x J α ( u x ) J α ( v x ) d x = 1 u δ ( u − v ) \displaystyle \int _{0}^{\infty}xJ_{\alpha}(ux) J_{\alpha }(유효),flac=flac {1}{u}}\flac(u-v)} α > -1/ 2 의 경우 행켈 변환은 상당히 임의적인[clarification needed 함수를 다양한 척도의 베셀 함수의 적분으로 표현할 수 있습니다. 구형 베셀 함수의 경우 직교 관계는 다음과 같습니다. ∫ 0 ∞ x 2 j α ( u x ) j α ( v x ) d x = π 2 u 2 δ ( u − v ) \displaystyle \int _{0}^{\infty }x^{\alpha }(ux)j_{\alpha }(유효)j_{\alpha }(유효), scap={pi }{2u^{2}}\cape(u-v)} α > -1 의 경우
베셀 방정식의 또 다른 중요한 특성은 아벨의 항등식 에서 따랐으며, 해들의 브론스키안을 포함한다.
A α ( x ) d B α d x − d A α d x B α ( x ) = C α x {\displaystyle A_{\alpha}(x){\frac {dB_{\alpha}}{dx}-{\frac {dA_{\alpha}}}{dx}} B_{\alpha }(x)=black {C_{\alpha}}}{x}} 여기 서α A 와α B는 베셀 방정식의 두 가지 해이고α , C는 (α 와 고려된 특정 베셀 함수에 따라) x와 독립적인 상수이다.특히, J α ( x ) d Y α d x − d J α d x Y α ( x ) = 2 π x {\displaystyle J_{\alpha}(x){\frac {dY_{\alpha}}{dx}-{\frac {dJ_{\alpha}}}{dx}} Y_{\alpha }(x)=black {2}{\pi x}} 그리고. I α ( x ) d K α d x − d I α d x K α ( x ) = − 1 x , \displaystyle I_{\alpha }(x){\frac {dK_{\alpha}}{dx}-{\frac {d} I_{\alpha }}{dx}}K_{\alpha }(x)=-{\frac {1}{x}}} α > -1 의 경우
α > -1 의 경우 xJ −α α x ) 허락하다
0 < > j α , 1 < > j α , 2 < > ⋯ < > j α , n < > ⋯ \displaystyle 0 <j_{\alpha,1} <j_{\alpha,2} <\cdots <j_{\alpha,n} <\cdots } 그럼 모두 양의 0이 되는 거야 J α ( z ) = ( z 2 ) α Γ ( α + 1 ) ∏ n = 1 ∞ ( 1 − z 2 j α , n 2 ) ({displaystyle J_{\alpha }(z)=paramfrac {\alpha}{\alpha}}{\Gamma(\alpha +1)}}}\param _{n=1}{\infty}\left(1-{\frac {z}}{j_{\alpha}{{\alpha}^{{{n}}}}}}}}}}}}오른쪽}})
(여기에서는 재현되지 않지만 참조에서 확인할 수 있는 다수의 다른 알려진 통합 및 ID가 있습니다.)
Jα , Yα , H (1) α 및 (2) α 반복 [45]
2 α x Z α ( x ) = Z α − 1 ( x ) + Z α + 1 ( x ) {\displaystyle {2\alpha }{x}Z_{\alpha }(x)=Z_{\alpha -1}(x)+Z_{\alpha +1}(x)} 그리고. 2 d Z α ( x ) d x = Z α − 1 ( x ) − Z α + 1 ( x ) , {\displaystyle 2gfrac {dZ_{\alpha }(x)}{dx}=Z_{\alpha -1}(x)-Z_{\alpha +1}(x)} 여기 서 Z는 J, Y , H (1) 또는 (2) 나타냅니다 .이 두 개의 동일성은 종종 다양한 다른 관계를 산출하기 위해 추가 또는 차감된다. 예를 들어, 이러한 방법으로 낮은 차수의 값(또는 낮은 차수의 값)이 주어진 고차(또는 높은 도함수)의 베셀 함수를 계산할 수 있습니다. 특히 다음과[46] ( 1 x d d x ) m [ x α Z α ( x ) ] = x α − m Z α − m ( x ) , ( 1 x d d x ) m [ Z α ( x ) x α ] = ( − 1 ) m Z α + m ( x ) x α + m . (\displaystyle\leftfrac{1}{x}{\frac{d}{frac}}\오른쪽) ^{m}\left [x^{\alpha }Z_{\alpha }(x)\right]&=x^{\alpha -m}Z_{\alpha -m}(x),\leftfrac {1}{x}{\frac {d}}}\right}\frac {\frac {d}}}}\fright}\alpha - m}\alpha - m}\right) ^{m}\left[{\frac {Z_{\alpha }(x)}{x^{\alpha }}\right]&=frac {Z_{\alpha +m}(x)}{x^{\alpha +m}}}}}. \end { aligned}}
수정 된 Bessel 함수는 유사한 관계를 따릅니다.
e ( x 2 ) ( t + 1 t ) = ∑ n = − ∞ ∞ I n ( x ) t n {\displaystyle e^{\displaystyle\frac {x}{x}}\right(t+{\frac {1}{t}\right)}=\sum _{n=-\infty}^{\infty}}I_{n}(x)t^{n}}}} 그리고. e z 왜냐하면 θ = I 0 ( z ) + 2 ∑ n = 1 ∞ I n ( z ) 왜냐하면 n θ {\displaystyle e^{z\cos \theta} = I_{0}(z)+2\sum _{n=1}^{\infty}I_{n}(z)\cos n\theta } 그리고. 1 2 π ∫ 0 2 π e z 왜냐하면 ( m θ ) + y 왜냐하면 θ d θ = I 0 ( z ) I 0 ( y ) + 2 ∑ n = 1 ∞ I n ( z ) I m n ( y ) . {\displaystyle {1}{2\pi }}\int _{0}^{2\pi }e^{z\cos(m\theta)+y\cos\theta }d\theta = I_{0}(z) I_{0}(y)+2\sum _{n=1}^{\infty}I_{n}(z) I_{mn}(y) }
반복 관계가 다음과 같습니다.
C α − 1 ( x ) − C α + 1 ( x ) = 2 α x C α ( x ) , C α − 1 ( x ) + C α + 1 ( x ) = 2 d C α ( x ) d x , 디스플레이 스타일 C_{\alpha -1}(x)-C_{\alpha +1}(x)&=snfrac {2\alpha }{x}C_{\alpha }(x),\C_{\alpha -1}(x)+ C_{\alpha +1}(x)&=2gcfrac {dC_{\alpha }(x)}{gc},\end{aligned}} 여기 서α C는 I 또는 eK αi πα 나타냅니다α .이러한 반복 관계는 이산 확산 문제에 유용합니다.
초월성 1929년, 칼 루드비히 시겔 은 θ 가 유리 하고 x가 대수적이고 [47] J(x ), ν J '(ν x ν J ( 초월수 라는 것 ν 같은 증명 K (x)[48] 것 ν
곱셈 정리 베셀 함수는 곱셈 정리에 따른다
λ − ν J ν ( λ z ) = ∑ n = 0 ∞ 1 n ! ( ( 1 − λ 2 ) z 2 ) n J ν + n ( z ) , \displaystyle \displayda ^{-\nu }J_{\nu }(\displayda z)=\sum _{n=0}^{\infty }{\frac {1}{n! }}\left({\frac {\lambda ^{2}\right)z}{2}\right)^{n}J_{\nu +n}(z),} 여기서 θ 와 θ 는 임의의 [49] [50] - 1 < 1 [49] 12 、 J가 Y 로 치환된 경우 에도 위의 식은 유지됩니다.수정된 베셀 함수와 β2 1 < 1 에 대한 유사한 동일성은 다음과 같다. λ − ν I ν ( λ z ) = ∑ n = 0 ∞ 1 n ! ( ( λ 2 − 1 ) z 2 ) n I ν + n ( z ) \displaystyle \displayda ^{-\nu }I_{\nu }(\displayda z)=\sum _{n=0}^{\infty }{\frac {1}{n! }}\left\frac(좌(좌){2}-1\우)z}{2}{n} I_{\nu +n}(z)} 그리고. λ − ν K ν ( λ z ) = ∑ n = 0 ∞ ( − 1 ) n n ! ( ( λ 2 − 1 ) z 2 ) n K ν + n ( z ) . {\displaystyle \displayda ^{-\nu }K_{\nu }(\displayda z)=\sum _{n=0}^{\infty}{\frac {(-1)^{n}}{n! }}\left\frac(좌(좌){2}-1\우)z}{2}\우) ^{n}K_{\nu +n}(z). }
베셀 함수의 0 부르제의 가설 베셀 자신은 원래 음이 아닌 정수 n에 대해 n 방정식 x ) = 0이 [51] 무한 한 수의 해를 갖는다는 것을 증명했다. 그러나 n (x ) 가 동일한 그래프에 표시될 경우, x = 0 n 의 다른 값에 대해 일치하는 0은 없습니다.이 현상은 베셀 함수를 연구한 19세기 프랑스 수학자의 이름을 따서 부르제의 가설 로 알려져 있다. 특히, 정수 n 0및 1 1에 대해 함수 Jn (x )n + m (x ) 는 x = 0 에 있는 그 가설은 1929년 [52] 루드비히 시겔에 의해 증명되었다.
초월성 1929년 시겔은 θ 가 합리적일 때, J(x) 와 J'( ν ν 초월적 이라는 것을 증명했고, K(x) [48] ν [53] 또한 특수값 J 1 3 = 0 1 }^(3)(\displaystyle J_{\ nu }^{(n)} ( 대한 상위 도함수 ( x ) 초월적 3}})=0 [53] .
수치적 접근법 베셀 함수의 0에 대한 수치 연구는 Gil, Segura & Teme(2007), Kravanja 등(1998) 및 Moler( 2004) 를 참조 한다.
수치 J의0 첫 번째 0(즉, j0,1 , j0,2 및 j0,3 )은 각각 [54]
「 」를 참조해 주세요. 메모들 ^ Weisstein, Eric W. "Spherical Bessel Function of the Second Kind" . MathWorld ^ Weisstein, Eric W. "Bessel Function of the Second Kind" . MathWorld ^ a b 아브라모위츠와 스테건, 360쪽, 9.1.10 ^ 아브라모위츠와 스테건, 페이지 358, 9.1.5 ^ a b Temme, Nico M. (1996). Special Functions: An introduction to the classical functions of mathematical physics (2nd print ed.). New York: Wiley. pp. 228–231. ISBN 0471113131 ^ "Hansen-Bessel Formula" .^ 왓슨, 페이지 176 ^ "Archived copy" . Archived from the original on 2010-09-23. Retrieved 2010-10-18 .{{cite web }}: CS1 maint: 제목으로 아카이브된 복사(링크 ) ^ "Integral representations of the Bessel function" . www.nbi.dk . Retrieved 25 March 2018 .^ Arfken & Weber, 11.1.17 연습. ^ 아브라모위츠와 스테건, 페이지 362, 9.1.69 ^ Szegő, Gábor (1975). Orthogonal Polynomials (4th ed.). Providence, RI: AMS.^ "Bessel Functions of the First and Second Kind" (PDF) . mhtlab.uwaterloo.ca . p. 3. Retrieved 24 May 2022 .^ NIST 수학 함수 디지털 라이브러리 , (10.8.1).2016년 10월 25일 회선으로 접속. ^ Weisstein, Eric W. "Bessel Function of the Second Kind" . MathWorld ^ a b 왓슨, 페이지 178 ^ 아브라모위츠와 스테건, 페이지 358, 9.1 .3, 9.1 .4 ^ 아브라모위츠와 스테건, 페이지 358, 9.1.6 ^ 아브라모위츠와 스테건, 360쪽, 9.1.25 ^ 아브라모위츠와 스테건, 페이지 375, 9.6.2, 9.6.10, 9. 6.11 ^ Dixon; Ferrar, W.L. (1930). "A direct proof of Nicholson's integral". The Quarterly Journal of Mathematics . Oxford: 236–238. doi :10.1093/qmath/os-1.1.236 . ^ 아브라모위츠와 스테건, 페이지 375, 9.6.3 , 9.6.5 ^ 아브라모위츠와 스테건, 페이지 374, 9.6.1 ^ Greiner, Walter; Reinhardt, Joachim (2009). Quantum Electrodynamics . Springer. p. 72. ISBN 978-3-540-87561-1 ^ 왓슨, 페이지 181 ^ Khokonov, M.Kh.(2004년)."에너지 손실의 방출에 의해 하드 Photons의 캐스케이드 과정".저널 실험 및 이론 물리학. 99(4):690–707.Bibcode:2004JETP...99..690K. doi:10.1134/1.1826160.S2CID 122599440..공식 나 S.Gradshteyn과 I.M.Ryzhik, 표 Integrals, 시리즈, 그리고 제품(Fizmatgiz, 모스크바, 1963년, 학술 출판부, 뉴욕, 1980년)에 소싱에서 파생됐죠 ^ 다음과 같이 언급됩니다. ^ 아브라모위츠와 스테건, 페이지 437, 10. 1.1 ^ 아브라모위츠와 스테건, 페이지 439, 10.1.25, 10. 1.26 ^ 아브라모위츠와 스테건, 438쪽, 10. 1.11 ^ 아브라모위츠와 스테건, 438쪽, 10. 1.12 ^ 아브라모위츠와 스테건, 페이지 439, 10. 1.39 ^ 아브라모위츠와 스테건, 페이지 439, 10.1.23, 10. 1.24 ^ 그리피스. 양자역학개론, 제2판, 154페이지 ^ Du, Hong (2004). "Mie-scattering calculation". Applied Optics . 43 (9): 1951–1956. Bibcode :2004ApOpt..43.1951D . doi :10.1364/ao.43.001951 . PMID 15065726 . ^ 아브라모위츠와 스테건, 364, 9.2.1페이지 ^ NIST 수학 함수 디지털 라이브러리 , 섹션 10.11 .^ 아브라모위츠와 스테건, 페이지 377, 9.7.1 ^ 아브라모위츠와 스테건, 페이지 378, 9.7.2 ^ Fröhlich and Spencer 1981 부록 B ^ 아브라모위츠와 스테건, 페이지 363, 9. 1.82 f. ^ Watson, G. N. (25 August 1995). A Treatise on the Theory of Bessel Functions ISBN 9780521483919 . Retrieved 25 March 2018 – via Google Books. ^ Gradshteyn, Izrail Solomonovich ; Ryzhik, Iosif Moiseevich ; Geronimus, Yuri Veniaminovich ; Tseytlin, Michail Yulyevich ; Jeffrey, Alan (2015) [October 2014]. "8.411.10.". In Zwillinger, Daniel; Moll, Victor Hugo (eds.). Table of Integrals, Series, and Products Academic Press, Inc. ISBN 978-0-12-384933-5 LCCN 2014010276 .^ Arfken & Weber, 섹션 11.2 ^ 아브라모위츠와 스테건, 페이지 361, 9.1.27 ^ 아브라모위츠와 스테건, 페이지 361, 9.1.30 ^ Siegel, Carl L. (2014). "Über einige Anwendungen diophantischer Approximationen". On Some Applications of Diophantine Approximations: a translation of Carl Ludwig Siegel's Über einige Anwendungen diophantischer Approximationen by Clemens Fuchs, with a commentary and the article Integral points on curves: Siegel's theorem after Siegel's proof by Clemens Fuchs and Umberto Zannier doi :10.1007/978-88-7642-520-2_2 . ISBN 978-88-7642-520-2 ^ a b James, R. D. (November 1950). "Review: Carl Ludwig Siegel, Transcendental numbers" . Bulletin of the American Mathematical Society . 56 (6): 523–526. doi :10.1090/S0002-9904-1950-09435-X . ^ a b 아브라모위츠와 스테건, 페이지 363, 9.1.74 ^ Truesdell, C. (1950). "On the Addition and Multiplication Theorems for the Special Functions" (PDF) . Proceedings of the National Academy of Sciences . 1950 (12): 752–757. Bibcode :1950PNAS...36..752T . doi :10.1073/pnas.36.12.752 PMC 1063284 PMID 16578355 . ^ Bessel, F. (1824) "Untersuchung des Theils der planetarischen Störungen", 베를린 압한들룬겐 , 제14조. ^ 왓슨, 페이지 484-485 ^ a b Lorch, Lee; Muldoon, Martin E. (1995). "Transcendentality of zeros of higher dereivatives of functions involving Bessel functions" . International Journal of Mathematics and Mathematical Sciences . 18 (3): 551–560. doi :10.1155/S0161171295000706 ^ 아브라모위츠 & 스테건, p409
레퍼런스 아브 밀턴, Stegun, Irene은 앤, eds.(1983년)[6월 1964년]."9장".Formulas, Graphs,과 수학적 표로 핸드 북 수학의 함수입니다.응용 수학 시리즈이다.Vol55(10원래 인쇄의 추가로 수정 작업과 교정을 9재판(1972년 12월) 제1판).워싱턴 DC, 뉴욕:미국 상무부, 표준국의 도버 출판사.를 대신하여 서명함. 지나갔으니까 355일, 435.아이 에스비엔 978-0-486-61272-0. LCCN 64-60036.MR0167642.LCCN 65-12253.또한 10장 참조하십시오. Arfken, George B. 및 Hans J. Weber, 물리학자를 위한 수학적 방법 , 제6판(Harcourt: San Diego, 2005).ISBN 0-12-059876-0 .Bowman, Frank의 Bessel 기능 소개 (도버: 뉴욕, 1958년). ISBN 0-486-60462-4 .Mie, G. (1908). "Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen" . Annalen der Physik . 25 (3): 377. Bibcode :1908AnP...330..377M . doi :10.1002/andp.19083300302 를 클릭합니다Olver, F. W. J. ; Maximon, L. C. (2010), "Bessel function" , in Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 를 클릭합니다Press, W. H. ; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007), "Section 6.5. Bessel Functions of Integer Order" , Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8 B Spain, M. G. Smith 수학물리학 함수 9장에서는 베셀 기능을 다룹니다. N.M. Temme, 특수 기능 수학물리학의 고전함수개론 (John Wiley and Sons, Inc., New York, 1996).ISBN 0-471-11313-1 .9장에서는 베셀 기능을 다룹니다. Watson, G. N., A Treatise on the Theory of Bessel Functions, 제2판, 케임브리지 대학 출판부(1995).ISBN 0-521-48391-3 .를 클릭합니다Weber, H. (1873), "Ueber eine Darstellung willkürlicher Functionen durch Bessel'sche Functionen", Mathematische Annalen , 6 (2): 146–161, doi :10.1007/BF01443190 , S2CID 122409461 Gil, A.; Segura, J.; Temme, N. M. (2007). Numerical methods for special functions . Society for Industrial and Applied Mathematics. 를 클릭합니다Kravanja, P. ; Ragos, O.; Vrahatis, M.N.; Zafiropoulos, F.A. (1998), "ZEBEC: A mathematical software package for computing simple zeros of Bessel functions of real order and complex argument", Computer Physics Communications , 113 (2–3): 220–238, Bibcode :1998CoPhC.113..220K , doi :10.1016/S0010-4655(98)00064-2 외부 링크 를 클릭합니다Lizorkin, P. I. (2001) [1994], "Bessel functions" , Encyclopedia of Mathematics EMS Press . 를 클릭합니다Karmazina, L. N.; Prudnikov, A.P. (2001) [1994], "Cylinder function" , Encyclopedia of Mathematics EMS Press . 를 클릭합니다Rozov, N. Kh. (2001) [1994], "Bessel equation" , Encyclopedia of Mathematics EMS Press . Wolfram 함수는 Bessel J, Y 함수에 페이지를 표시하고 Bessel I , K 함수를 수정하였습니다. 페이지에는 공식, 함수 평가자 및 그림 계산기가 포함됩니다. Wolfram Mathworld – 베셀 함수는 제1종 입니다.Librow 함수 핸드북의 Bessel 함수ν J, Y, Iν ν 및 Kν .F. W. J. Olver, L. C. Maximon, Bessel 함수(수학 함수 디지털 라이브러리 10장) Moler, C. B. (2004). Numerical Computing with MATLAB (PDF) . Society for Industrial and Applied Mathematics. Archived from the original (PDF) on 2017-08-08.
























 항켈 함수로 표현할 수 있습니다.
항켈 함수로 표현할 수 있습니다.


































![{\displaystyle {\begin{aligned}I_{\alpha }(z)={\frac {1}{{\sqrt {2\pi z}}{\sqrt[{4}]{1+{\frac {\alpha ^{2}}{z^{2}}}}}}}\exp \left(-\alpha \operatorname {arsinh} \left({\frac {\alpha }{z}}\right)+z{\sqrt {1+{\frac {\alpha ^{2}}{z^{2}}}}}\right)\left(1+O\left({\frac {1}{z{\sqrt {1+{\frac {\alpha ^{2}}{z^{2}}}}}}}\right)\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e8dffc51e4f1eb138fc189cc6349721add2bb02)















![{\displaystyle {\begin{aligned}J_{\nu }(z)&={\frac {\left({\frac {z}{2}}\right)^{\nu }}{\Gamma \left(\nu +{\frac {1}{2}}\right){\sqrt {\pi }}}}\int _{-1}^{1}e^{izs}\left(1-s^{2}\right)^{\nu -{\frac {1}{2}}}\,ds\\[5px]&={\frac {2}{{\left({\frac {z}{2}}\right)}^{\nu }\cdot {\sqrt {\pi }}\cdot \Gamma \left({\frac {1}{2}}-\nu \right)}}\int _{1}^{\infty }{\frac {\sin zu}{\left(u^{2}-1\right)^{\nu +{\frac {1}{2}}}}}\,du\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/248363b3af99701e32dcec48127f0dfc6e7586bf)
![{\displaystyle \int _{0}^{1}xJ_{\alpha }\left(xu_{\alpha ,m}\right)J_{\alpha }\left(xu_{\alpha ,n}\right)\,dx={\frac {\delta _{m,n}}{2}}\left[J_{\alpha +1}\left(u_{\alpha ,m}\right)\right]^{2}={\frac {\delta _{m,n}}{2}}\left[J_{\alpha }'\left(u_{\alpha ,m}\right)\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4901ce8ec95f647c69297f8a6a92d245466ba632)
![{\displaystyle \int _{0}^{1}x^{2}j_{\alpha }\left(xu_{\alpha ,m}\right)j_{\alpha }\left(xu_{\alpha ,n}\right)\,dx={\frac {\delta _{m,n}}{2}}\left[j_{\alpha +1}\left(u_{\alpha ,m}\right)\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de6fbc1b8ac85fb7dd6253a931d1b78cec9b89ae)












![{\displaystyle {\begin{aligned}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{m}\left[x^{\alpha }Z_{\alpha }(x)\right]&=x^{\alpha -m}Z_{\alpha -m}(x),\\\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{m}\left[{\frac {Z_{\alpha }(x)}{x^{\alpha }}}\right]&=(-1)^{m}{\frac {Z_{\alpha +m}(x)}{x^{\alpha +m}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c59565e99a36cfef8426d543521d8e4df7bc07a2)











