미에 산란

맥스웰 방정식에 대한 미에 해법(로렌츠-미에 해법, 로렌츠-미에 해법 또는 미에 산란이라고도 한다)은 동질 구에 의한 전자기 평면파의 산란을 설명한다. 용액은 구면 다극선 부분파의 무한 계열의 형태를 취한다. 구스타프 미에(Gustav Mie)의 이름을 따서 지은 것이다.

미에 용액이라는 용어는 또한 층화된 구체 또는 무한 실린더에 의한 산란을 위한 맥스웰 방정식의 용액이나 용액의 방사상 및 각도 의존성에 대한 별도의 방정식을 작성할 수 있는 다른 기하학적 용액에도 사용된다. 미에 이론이라는 용어는 때때로 이 해법과 방법의 집합에 사용된다; 그것은 독립적인 물리적 이론이나 법칙을 지칭하지 않는다. 보다 넓게 보면, "미 산란" 공식은 산란 입자의 크기가 훨씬 작거나 훨씬 큰 것이 아니라 빛의 파장에 필적하는 상황에서 가장 유용하다.

미에 산란(비분자 산란 또는 에어로졸 입자 산란이라고도 함)은 대기의 하위 4,500m(15,000ft)에서 발생하며, 입사 광선의 파장과 거의 동일한 직경을 가진 많은 본질적으로 구형 입자가 존재할 수 있다. 미에 산란 이론은 크기 상한이 없고, 큰 입자에 대해서는 기하학적 광학 한계로 수렴한다.^[1]

소개

구체의 산란 문제에 대한 미에 용액의 현대적인 제형은 J. A. Stratton의 전자기 이론과 같은 많은 책에서 찾을 수 있다.^[2] 이 제형에서는 산란장뿐만 아니라 입사 평면 파형이 방사 구형 벡터 구형 고조파까지 확장된다. 내부 장은 정규 벡터 구형 고조파들로 확장된다. 구면 표면에 경계 조건을 시행함으로써 산란장의 확장 계수를 계산할 수 있다.

산란된 빛의 파장보다 훨씬 크거나 훨씬 작은 입자의 경우 시스템의 동작을 설명하기에 충분한 간단하고 정확한 근사치가 있다. 그러나 대기의 물방울, 페인트의 라텍스 입자, 우유를 포함한 유전의 물방울, 생물학적 세포와 세포 구성 요소 등 파장의 크기가 몇 가지 순서 내에 있는 물체의 경우 보다 상세한 접근이 필요하다.^[3]

미에 솔루션은^[4] 개발자인 독일 물리학자 구스타프 미에(Gustav Mie)의 이름을 딴 것이다. 덴마크 물리학자 루드비그 로렌츠 등은 유전체 구에 의한 전자파 산란 이론을 독자적으로 개발했다.

형식주의는 구형 물체 내외부의 전기장과 자기장을 계산할 수 있게 하며 일반적으로 빛이 얼마나 산란되는지(전체 광학 단면) 또는 어디로 가는지(형성 인자)를 계산하는 데 사용된다. 이러한 결과의 주목할 만한 특징은 미에 공진이며, 크기가 특히 강하고 약하게 분산되어 있다.^[5] 이는 작은 입자의 경우 레일리 산란, 큰 입자의 경우 레일리-간스-드바이 산란(레일리 경, 리차드 간스, 피터 데비 후)과는 대조적이다. 공명 및 미에 산란(Mie 산란)의 다른 특징의 존재는 산란된 빛을 사용하여 입자 크기를 측정할 때 특히 유용한 형식주의로 만든다.

근사치

Rayleigh 근사치(scattering)

레일리 산란은 빛의 파장보다 훨씬 작은 구에 의한 빛의 탄성 산란을 묘사한다. 산란 방사선의 강도 1은 다음과 같다.

$(\displaystyle I=I_{0}\left({\frac {1+\cos ^{2}\theta }{2R^{2}}}\right)\left({\frac {2\pi }{\lambda }}\right)^{4}\left({\frac {n^{2}-1}{n^{2}+2}}\right)^{2}\left({\frac {d}{2}}\right)^{6},}$

여기서 나는₀ 입자와 상호작용하기 전의 광도, R은 입자와 관찰자 사이의 거리, θ은 산란각, λ은 고려 중인 빛의 파장, n은 입자의 굴절률, d는 입자의 지름이다.

Rayleigh 산란이 입자의 크기와 파장의 크기에 크게 좌우된다는 것은 위의 방정식에서 알 수 있다. Rayleigh 산란 방사선의 강도는 파장에 대한 입자 크기 대 파장의 비율이 증가함에 따라 빠르게 증가한다. 더욱이 레일리 산란 방사선의 강도는 전방과 후방 방향에서 동일하다.

레일리 산란 모델은 입자 크기가 입사 방사선의 파장의 약 10%보다 커지면 분해된다. 이보다 더 큰 치수의 입자의 경우 미에의 산란 모델을 사용하여 산란 방사선의 강도를 찾을 수 있다. 미에 산란 방사선의 강도는 단순한 수학적 표현보다는 무한한 일련의 용어들의 합계에 의해 주어진다. 그러나 이 입자 크기의 범위에서 산란하는 것은 몇 가지 측면에서 Rayleigh 산란과 다르다는 것을 알 수 있다. Rayleigh 산란과는 거의 파장과 무관하며, 반대 방향보다 전방 방향에서 더 크다. 입자 크기가 클수록 빛이 전방으로 흩어진다.

하늘의 푸른색은 대기 중의 가스 입자의 크기가 가시광선의 파장보다 훨씬 작기 때문에 레일리 산란에서 비롯된다. 레일리 산란은 파장이 짧아 블루라이트의 경우 파장이 다른 색상보다 훨씬 크다. 햇빛이 대기를 통과함에 따라, 그것의 파란색 성분은 대기 가스에 의해 강하게 산란된 레일리지만 더 긴 파장(예: 빨강/노랑) 성분은 그렇지 않다. 그러므로 태양으로부터 직접 도달하는 햇빛은 약간 노란색으로 보이는 반면, 나머지 하늘에 흩어져 있는 빛은 파란색으로 보인다. 일몰과 일몰 중에는 광선이 지구 표면 근처의 고밀도 공기를 통해 이동해야 하는 거리가 넓기 때문에 전송되는 빛의 스펙트럼에 대한 레일리 산란 효과는 훨씬 더 크다.

이와는 대조적으로 구름을 구성하는 물방울은 가시광선의 파장과 비교가능한 크기이며, 산란은 레일리보다는 미에의 모델에 의해 설명된다. 여기서, 가시광선의 모든 파장은 대략 비슷하게 흩어지고, 따라서 구름은 흰색이나 회색으로 보인다.

레일리-간스 근사

Rayleigh-Gans 근사치는 입자의 상대적 굴절률이 환경의 굴절률에 가까울 때 빛 산란에 대한 대략적인 해결책이며, 그 크기는 빛의 파장을 n - 1로 나눈 것에 비해 훨씬 작다. 여기서 n은 굴절률이다.^[3]

${\displaystyle n-1 \ll 1}$

${\displaystyle kd n-1 \ll 1}$

여기서 $k$ ${\textstyle k}$은 빛의 파장($$= 2 $\frac{\pi }{}$ $\frac{}{}$λ {\$textstyle$ k$={\frac {2\pi }{\lambda$}}}})$$이며 d ${\displaystyle d}$은 입자의 선형 치수를 가리킨다$$. 전자의 조건은 종종 "optically soft"라고 불리며, 근사치는 임의 형태의 입자를 포함한다.^[3]

판 데 헐스트의 비정상적 회절 근사치

변칙적인 회절 근사치는 큰(파장에 비해)과 광학적으로 부드러운 구에 유효하다. 광학 맥락에서 부드러운 것은 입자의 굴절률(m)이 환경의 굴절률과 약간 다를 뿐이며, 입자는 파장을 작은 위상 변화로만 귀속시킨다는 것을 의미한다. 이 근사치의 소멸 효율은 다음과 같다.

${\displaystyle Q=2-{\frac {4}{p}\p}\sin p+{\frac {4}{p^{2}}(1-\cos p),}$

여기서 Q는 산란 효율 계수로서 산란 단면과 기하학적 단면 πa의² 비율로 정의된다.

p = 4πa(n - 1)/λ이라는 용어는 물리적인 의미로 구의 중심을 통과하는 파동의 위상지연(phase delay)을 가지고 있는데, 여기서 a는 구의 반지름이며, n은 구의 내외부 굴절률이며, λ 빛의 파장은 has이다.

이 방정식의 집합은 (1957년)에 판 데 헐스트에 의해 처음 설명되었다.^[5]

수학

구형 나노입자에 의한 산란은 입자 크기에 관계없이 정확히 해결된다. x축을 따라 편극화된 z축을 따라 전파되는 평면파에 의한 산란을 고려한다. 입자의 유전체 및 자기 투과성은 환경을$$ 위해$$ ${\displaystyle {\epsilon \mathrm{}}_{}}$1 {\$displaystyle \varepsilon _{1}$및 ${\displaystyle {\mu 1\mathrm{}}_{}}$ ${\$$\epsilon {\displaystyle }$ ${\displaystyle \varepsilon }$ 및$$ $\mu {\displaystyle }$ ${\displaystystyleane \mu}$이다.

산란 문제를 해결하기 위해서는 먼저 입자 내외의 장이 이를 만족시켜야 하기 때문에 벡터 헬름홀츠 방정식의 해답을 구면 좌표로 작성한다.^[3] 헬름홀츠 방정식:

${\displaystyle \nabla ^{2}\mathbf {E} +{k}^{2}\mathbf {E} =0,\\\\\ \nabla ^{2}\mathbf {H}+{k}^{2}\mathbf {H} =0}$

in addition to the Helmholtz equation, the fields must satisfy the conditions ${\displaystyle \nabla \cdot \mathbf {E} =\nabla \cdot \mathbf {H} =0}$ and ${\displaystyle \nabla \times \mathbf {E} =i\omega \mu \mathbf {H} }$, ${\displaystyle \nabla \times \mathbf {H} =-$$i\omega \varepsilon \mathbf {E$ 벡터 구형 고조파에는 다음과 같이 소개된 모든 필요한 특성이 있다.

${\displaystyle {\mathbf{M}}_{}}$ $o$ ${\displaystyle {{}_{}^{}}_{}}$ n = ${\displaystyle {}_{}\mathrm{}\times }$ (${\displaystyle {}_{}}$r ${\displaystyle \psi {}_{}}$ ${\displaystyle {{}_{}^{}}_{}}$ ${\displaystyle e_{}}$ n ) ${\$ \$psi \{^{e}_{$o}$mn}\$$rig) —자기 고조파($TE)

${\displaystyle {\mathbf{N}}_{}}$ ${\displaystyle {{}_{}^{}}_{}}$ ${\displaystyle {{}_{}^{}}_{}}$ e ${\displaystyle n_{}}$= ${\displaystyle \times \frac{\mathrm{}}{}}$ ${\displaystyle \frac{\times }{}}$ × ${\displaystyle \frac{{{}_{}^{}}_{}}{}}$ n ${\displaystyle \frac{{}_{}}{}}$ ${\$ —$$ - 전기 고조파화

어디에

${\displaystyle {\psi _{emn}=\cos m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r)}}}}}}}$

${\displaystyle {\psi _{omn}=\sin m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r)}}}}}}}}$

및 ${\displaystyle {Pn}_{}^{}}$ ${\displaystyle {}_{}^{}\cos }$ ${\displaystyle \theta }$ ) ${\displaystyle P_{n}^{m}(\cos \theta$ )$$—$$ 관련 범례 다항식 및 z ${\displaystyle n_{}k}$ r${\displaystyle }$) ${\displaystyle z_{n}({k}r)$—$$ 모든 구형 베셀 함수.

다음으로 벡터 구형 고조파에서 입사 평면 파형을 확장한다.

${\displaystyle \mathbf {E} _{inc}=E_{0}e^{ikr\cos \theta }\mathbf {e} _{x}=E_{0}\sum _{n=1}^{\infty }i^{n}{\frac {2n+1}{n(n+1)}}\left(\mathbf {M} _{o1n}^{(1)}(k,\mathbf {r} )-i\mathbf {N} _{e1n}^{(1)}(k,\mathbf {r} )\right)}$

${\displaystyle \mathbf {H} _{inc}={\frac {-k}{\omega \mu }}E_{0}\sum _{n=1}^{\infty }i^{n}{\frac {2n+1}{n(n+1)}}\left(\mathbf {M} _{e1n}^{(1)}(k,\mathbf {r} )+i\mathbf {N} _{o1n}^{(1)}(k,\mathbf {r} )\right)}$

여기서 위첨자$({\displaystyle 1}$) ${\displaystyle(1)}$는 함수의 반경 부분 $\psi {\displaystyle {}_{}}$ ${\displaystyle {{}_{}^{}}_{}}$ ${\displaystyle {{}_{}^{}}_{}}$ ${\displaystyle m_{}}$ ${\displaystyle {{}_{}^{}}_{}}$ ${\$이(가) 구형$$ Besel 함수임을 의미한다$$. 팽창 계수는 폼의 통합을 통해 얻는다.

${\displaystyle {\frac {\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {E} _{inc}\cdot \mathbf {M} _{^{e}_{o}mn}^{(1)}\sin \theta d\theta d\varphi }{\int _{0}^{2\pi }\int _{0}^{\pi } \mathbf {M} _{^{e}_{o}mn}^{(1)} ^{2}\sin \theta d\theta d\varphi }}}$

이 경우 분자의 각도$$ $over{\displaystyle }$ ${\$$displaystyle m\neq 1}$에 대한 적분은 0이므로 m${\displaystyle }m{\displaystyle }$ ${\displaystyle 1}$ ${\$$displaystyle \varphi }$의 모든 계수는 0이다$$.

그 후 다음과 같은 조건이 부과된다.

1) 구체와 환경의 경계에 대한 접점 조건(사건, 내부, 산란계수의 확장계수를 연관시킬 수 있음)

2) 용액이 원점에 경계되는 조건(따라서 생성함수의 방사형 부분에서는 $\psi {\displaystyle {}_{}}$ ${\displaystyle {{}_{}^{}}_{}}$ ${\displaystyle o_{}}$ e m$$n {\$displaystyle \psi _{^{e}_{o$}mn$\}\}\}\},$ 내부장에서는 Besel 구형 함수가 선택됨)

3) 산란장의 경우 무한대의 점증상학은 이탈하는 구형파에 해당한다(이와 관련하여 발생함수의 반경 부분에 있는 산란장에 대해서는 for ${\displaystyle {{}_{}^{}}_{}}$ ${\displaystyle e_{}}$ m n ${\$제1종 구형$$ 한켈 함수를 선택한다).

산란장은 벡터 고조파 팽창의 관점에서 다음과 같이 기록된다.

${\displaystyle \mathbf {E} _{s}=\sum _{n=1}^{\infty }E_{n}\left(ia_{n}\mathbf {N} _{e1n}^{(3)}(k,\mathbf {r} )-b_{n}\mathbf {M} _{o1n}^{(3)}(k,\mathbf {r} )\right)}$

${\displaystyle \mathbf {H} _{s}={\frac {k}{\omega \mu }}\sum _{n=1}^{\infty }E_{n}\left(a_{n}\mathbf {M} _{e1n}^{(3)}(k,\mathbf {r} )+ib_{n}\mathbf {N} _{o1n}^{(3)}(k,\mathbf {r} )\right)}$

here the superscript ${\displaystyle (3)}$ means that in the radial part of the functions ${\displaystyle \psi _{^{e}_{o}mn}}$ are spherical Hankel functions, and ${\displaystyle E_{n}={\frac {i^{n}E_{0}(2n+1)}{n(n+1)}}}$,

내부 필드:

${\displaystyle \mathbf {E} _{1}=\sum _{n=1}^{\infty }E_{n}\left(-id_{n}\mathbf {N} _{e1n}^{(1)}(k_{1},\mathbf {r} )+c_{n}\mathbf {M} _{o1n}^{(1)}(k_{1},\mathbf {r} )\right)}$

${\displaystyle \mathbf {H} _{1}={\frac {-k_{1}}{\omega \mu _{1}}}\sum _{n=1}^{\infty }E_{n}\left(d_{n}\mathbf {M} _{e1n}^{(1)}(k_{1},\mathbf {r} )+ic_{n}\mathbf {N} _{o1n}^{(1)}(k_{1},\mathbf {r} )\right)}$

${\displaystyle k={\frac {\omega }{c}}n}$ is the wave vector outside the particle ${\displaystyle k_{1}={\frac {\omega }{c}}{n_{1}}}$ is the wave vector in the medium from the particle material, ${\displaystyle n}$ and ${\displaystyle n_{1}}$ are the refractive indices of t그는 중간과 입자,

인터페이스 조건을 적용한 후 계수에 대한 식을 구한다.

${\displaystyle c_{n}(\omega )={\frac {\mu _{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho )-\mu _{1}\left[\rho j_{n}(\rho )\right]'h_{n}(\rho )}{\mu _{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}}}$

${\displaystyle d_{n}(\omega )={\frac {\mu _{1}n_{1}n\left[\rho h_{n}(\rho )\right]'j_{n}(\rho )-\mu _{1}n_{1}n\left[\rho j_{n}(\rho )\right]'h_{n}(\rho )}{\mu n_{1}^{2}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu _{1}n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}},}$

${\displaystyle b_{n}(\omega )={\frac {\mu _{1}\left[\rho j_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'j_{n}(\rho )}{\mu _{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}}}$

${\displaystyle a_{n}(\omega )={\frac {\mu n_{1}^{2}\left[\rho j_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu _{1}n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]'j_{n}(\rho )}{\mu n_{1}^{2}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu _{1}n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}},}$

어디에

$\displaystyle \rho =ka}$

${\displaystyle {\rho }_{}}$ ${\displaystyle {1\mathrm{}}_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \rho _{1}=k_{1}a},$ ${\displaystyle a}$은(는) 구의 반지름이다$$.

${\displaystyle j_{}}$ ${\displaystyle n_{}}$ ${\$와 h$${\$displaystyle h_{n}}$는 각각 제1종 베셀과 한클의 구형 함수를 나타낸다$$.

산란과 소멸 교차점

Mie 이론을 사용하여 일반적으로 계산되는 값에는 ${\displaystyle {소멸}_{}}$ $Q{\displaystyle {}_{}}$ e ${\$ 산란 Q ${\displaystyle s_{}}$ ${\$ 흡수 $Q{\displaystyle {}_{}}$ ${\displaystyle a_{}}$ ${\$에 대한 효율성 계수가 포함된다$.$^[6][7] 이러한 효율 계수는 입자 보호 구역에 대한$$ i {\$displaystyle \sigma _{i$ ${\displaystyle {Qi}_{}}$ =${\displaystyle {}_{}\sigma \frac{{}_{}}{}}$ ${\displaystyle \frac{i_{}}{}}$ ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$ ${\$ a$^{2}}:$ a 입자 반지름이다$.$ 멸종의 정의에 따르면

${\displaystyle {\sigma }_{}}$ ${\displaystyle e_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle s_{}}$+ ${\displaystyle {}_{}}$ ${\displaystyle a_{}}$ ${\$ 및$$ ${\displaystyle Q_{}}$e = ${\displaystyle Q_{}}$ ${\displaystyle s_{}{}_{}}$+ ${\displaystyle {}_{}}$ a ${\$

산란 및 소멸 계수는 무한 계열로 나타낼 수 있다.

${\displaystyle Q_{s}={\frac {2}{k^{2}a^{2}}\sum _{n=1}^{n1}{n1}{n+1)(a_{n}+b_{n} ^{2}}}}}}}}$

${\displaystyle Q_{e}={\frac {2}{k^{2}a^{2}}\sum _{n=1}^{n1}{n1}{n+1)\re(a_{n}+b_{n}}}}}}}}}$

하위 파장 입자에 적용

만약 입자의 크기가 물질의 몇 개의 파장과 같다면, 흩어진 장에는 몇 가지 특징이 있다. 더 나아가 로터를 잡아 자기장을 얻어내기 때문에 전기장의 형태에 대해 이야기하겠다.

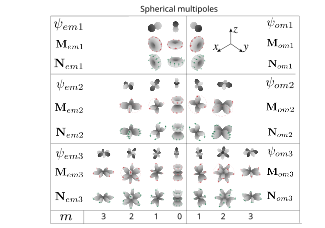
모든 Mie 계수는 주파수에 따라 달라지며 분모가 0에 가까울 때 최대값을 갖는다(복잡한 주파수에 대해 0과 실제 동일성이 달성된다). 이 경우, 특정 고조파 한 개의 기여도가 산란에서 지배하는 것이 가능하다. 그러면 입자에서 먼 거리에서 산란장의 방사선 패턴은 벡터 구형 고조파 각 부분의 해당 방사선 패턴과 유사할 것이다. The harmonics ${\displaystyle \mathbf {N} _{^{e}_{o}m1}}$ correspond to electric dipoles (if the contribution of this harmonic dominates in the expansion of the electric field, then the field is similar to the electric dipole field), ${\displaystyle \mathbf {M} _{^{e}_{o}m1}}$ correspond to the electric field of the magnetic dipole, ${\displaystyle \mathbf {N} _{^{e}_{o}m2}}$ and ${\displaystyle \mathbf {M} _{^{e}_{o}m2}}$ - electric and magnetic quadrupoles, ${\displaystyle \mathbf {N} _{^{e}_{o}m3}}$ and ${\displaystyl$$e \mathbf {M} _{^{e}_{o}m3}}$ $$- 팔진골 등 산란계수의 최대치(위상이 $\pi {\displaystyle }$ ${\displaystyle \pi }$으로 변경될 뿐만 아니라$)$를 멀티폴 공진이라고 한다.

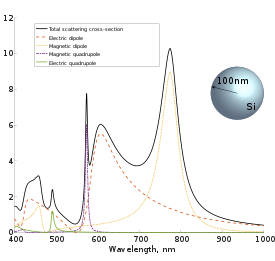
산란 단면이 파장에 대한 의존성과 특정 공명도의 기여도는 입자 물질에 따라 크게 달라진다. 예를 들어 반지름이 100nm인 금 입자의 경우 광학 범위에서 산란하는 전기 쌍극자의 기여도가 우세하며, 실리콘 입자의 경우 자기 쌍극과 4극 공진성이 두드러진다. 금속 입자의 경우 산란 단면에서 볼 수 있는 피크를 국부 플라스몬 공명이라고도 한다.

작은 입자나 긴 파장의 한계에서는 산란 단면에서 전기 쌍극자 기여가 지배적이다.

입사 평면 파동의 다른 방향

x-극화 평면 파형의 경우, z축을 따라 발생한 경우, 모든 필드의 분해는 m=1과의 고조파만 포함했지만, 임의의 입사 파형의 경우는 그렇지 않다.^[8] 회전 평면 파형의 경우, 예를 들어 회전하는 동안 벡터 구형 고조파들이 위그너 D 매트릭스에 의해 서로를 통해 변환된다는 사실을 이용하여 팽창 계수를 얻을 수 있다.

이 경우 산란된 장은 가능한 모든 고조파들에 의해 분해된다.

${\displaystyle \mathbf {E} _{s}=\sum _{n=1}^{n=1}^{n}E_{0}(D_{Memn}\mathbf {M} _{emn}^{(3)}(k,\mathbf {r} )+D_{Momn}\mathbf {M} _{omn}^{(3)}(k,\mathbf {r} )+D_{Nemn}\mathbf {N} _{emn}^{(3)}(k,\mathbf {r} )+D_{Nomn}\mathbf {N} _{omn}^{(3)}(k,\mathbf {r} ))}$

그런 다음 산란 단면은 다음과 같이 계수 단위로 표현된다.^[9]

${\displaystyle C_{sca}={\frac {2\pi }{\pi a^{2}k^{2}}}\sum _{n=1}^{\infty }{\frac {n(n+1)}{(2n+1)}}\times {\Bigl [}\sum \limits _{m=1}^{n}{\frac {(n+m)!}{{(n-m)!}}}}}(D_{Memn} ^{2}+ D_{Momn} ^{2}+ D_{Nemn} ^{Nemn} ^{2}+D_{Me0n} ^{2}+2 D_{Ne0n} ^{2}+2D_{Ne0n}{Bigr ]}.}$

커커 효과

Kerker 효과는 여러 가지 다중홀 반응이 나타나 무시할 수 없을 때 나타나는 방향성을 산란시키는 현상이다.

1983년 케커, 왕, 자일스의^[10] 연구에서는 $\mu {\displaystyle }$ ${\displaystyle \mathrm{\mu }}$1 ${\displaystyle \mu \neq 1}$의 입자에 의한 산란 방향이 조사되었다$$. 특히 $\mu {\displaystyle }$= ${\displaystyle \mu }$ = ${\displaystyle \mu =\varepsilon }$의 가상 입자에 대해서는 역분산을 완전히 억제하는 것으로 나타났다. 이는 반사 및 전달이 입사각과 무관하고 일정한 굴절 지수를 갖는 평면 표면에서 반사되는 자일스와 와일드 결과의 구면 표면으로의 확장으로 볼 수 있다.^[11]

또한 전방 및 후방 방향의 산란 단면은 단순히 Mie 계수 단위로 표현된다.^[12][13]

${\displaystyle C_{sca}^{backward}={\frac {1}{a^{2}k^{2}}:{\bigg }{n=1}^{n=1}{n1}^{n1}{n+1)(-1)^{n}(a_{n}-b_{n}}}}}{bigg}{}}{}}}}}}}}}}}}}}}}{{{{{}}}}}}}}}}:{2}}:}}}}}}}}}}}:{2}}:$

${\displaystyle C_{sca}^{forward}={\frac {1}{a^{2}k^{2}}:{\bigg }}{n=1}^{n1}{n+1}{n1}{n}}}}{n+1}{n}}}{\bigg }:{2}}: {n}$

특정 계수의 조합에 대해서는 위의 식을 최소화할 수 있다.

그래서, 예를 들면 n1{\displaystyle n> 1}으로 용어가 최소로 후방 산란에 해당하고(전기 자기 쌍극 안테나 크기에 단계에 있지만 이것 또한 'first 커커'이라고 하거나 'zero-backward 평등하다(쌍극자 근사),(1− b1))0{\displaystyle(a_{1}-b_{1})=0}무시할 수 있다.intensity condition'^[14]). ${\displaystyle \mathrm{그리고}}{\displaystyle }$( ${\displaystyle {1\mathrm{}}_{}}$+ ${\displaystyle {b\mathrm{}}_{}}$)${\displaystyle }$= 0 ${\displaystyle (a_{1}+b_{1}=0})$은 전방 산란에서 최소값에 해당하며$$, 이를 '제2의 커커 조건'(또는 '0에 가까운 전방 강도 조건')이라고도 한다. 광학 정리에서는 패시브 입자$({\displaystyle {1\mathrm{}}_{}}$=${\displaystyle }$- b ${\displaystyle {1\mathrm{}}_{}}$) ${\displaystyle(a_${1}=-$b_{1}})$이 불가능하다는$$ 것을 보여준다.^[15] 문제의 정확한 해결을 위해서는 모든 멀티폴의 기여도를 고려할 필요가 있다. 전기와 자석 쌍극의 합은 Huygens 소스를 형성한다.

유전체 입자의 경우 자기 이중극 공명의 파장보다 긴 파장에서 최대 전방 산란이 관찰되고, 짧은 파장에서 최대 후방 산란이 관찰된다.^[17]

나중에, 다른 종류의 효과들이 발견되었다. 예를 들어, 전방과 후방 산란장(측면 비산 패턴), 광역학적 커커 효과,^[18][19][20] 음향 산란에서 그리고 식물에서도 발견되는 거의 완전한 동시 억제가 있는 가로 커커 효과.^[21]

유튜브에는 그 효과에 대한 설명이 담긴 짧은 동영상도 있다.

디아디드 그린의 구 기능

그린의 함수는 다음과 같은 방정식에 대한 해법이다.

${\displaystyle \nabla \times \nabla \times {\bf {\hat {G}}}(\omega ,\mathbf {r} ,\mathbf {r} ')=\left({\frac {\omega }{c}}\right)^{2}\varepsilon (\mathbf {r} ,\omega ){\bf {\hat {G}}}(\omega ,\mathbf {r} ,\mathbf {r} ')+{\bf {\hat {1}}}\delta (\mathbf {r} -\mathbf {r} '),}$

r<>은 어디서 1^{\displaystyle{\hat{\bf{1}}}}— 단위 행렬 ε(r, ω))ε 1(ω){\displaystyle \varepsilon(\mathbf{r},\omega)=\varepsilon_{1}(\omega)};{\displaystyle r<.}, r을에 ε(r, ω))ε{\displaystyle \varepsilon(\mathbf{r},\omega)=\varepsilon};a {\display$style$r$a$}. 모든 필드가 벡터적이므로 녹색 함수는 3 X 3 행렬로 다이디치(dyadic)라고 한다. 필드가 다음과 같이 기록될 때 시스템에서 양극화 $P{\displaystyle \mathbf{}}$( ${\displaystyle r\mathbf{}}$) ${\displaystyle \mathbf {P}(\mathbf {r} )$가 유도되는$$ 경우

${\displaystyle \mathbf {E} ^{\omega }({\mathbf {r} })=\omega ^{2}\mu \int \limits _{V}dV'{\hat {\bf {G}}}({\bf {r,r'}},k)\mathbf {P} ^{\omega }(\mathbf {r} ')}$

필드와 같은 방법으로 그린의 기능은 벡터 구면 고조파로 분해될 수 있다.^[22] 디아디드 그린의 자유 공간 기능 issa:^[23]

${\displaystyle {\hat {\bf {G}}}^{0}({\mathbf {r} ,\mathbf {r} ',k})={\frac {\mathbf {e_{r}} \otimes \mathbf {e_{r}} }{k^{2}}}\delta (\mathbf {r} -\mathbf {r} ')+{\frac {ik}{4\pi }}\sum _{n=1}^{\infty }\sum _{m=0}^{n}(2-\delta _{m,0}){\frac {2n+1}{n(n+1)}}{\frac {(n-m)!}{{n+m!}}}\cdot }$

${\displaystyle \left\{{\begin{array}{l}\cdot {\Bigl (}(\mathbf {M} _{emn}^{(1)}[k,\mathbf {r} ]\otimes {\mathbf {M} }_{emn}^{(3)}[k,\mathbf {r} ']+\mathbf {M} _{omn}^{(1)}[k,\mathbf {r} ]\otimes {\mathbf {M} }_{omn}^{(3)}[k,\mathbf {r} '])+({\mathbf {N} }_{emn}^{(1)}[k,\mathbf {r} ]\otimes {\mathbf {N} }_{emn}^{(3)}[k,\mathbf {r} ']+\mathbf {N} _{omn}^{(1)}[k,\mathbf {r} ]\otimes {\mathbf {N} }_{omn}^{(3)}[k,\mathbf {r} ']){\Bigr )},{\text{if }}r<r'\\\cdot {\Bigl (}(\mathbf {M} _{emn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {M} }_{emn}^{(1)}[k,\mathbf {r} ']+\mathbf {M} _{omn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {M} }_{omn}^{(1)}[k,\mathbf {r} '])+({\mathbf {N} }_{emn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {N} }_{emn}^{(1)}[k,\mathbf {r} ']+\mathbf {N} _{omn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {N} }_{omn}^{(1)}[k,\mathbf {r} ']){\Bigr )},{\text{if }}r>r'\end{array}}\right.}$

구체의 존재에서는 그린의 기능도 벡터 구면 고조파로 분해된다. 그 모양은 $r{\displaystyle \mathbf{}}$ ${\$과(와) r$display$ {\displaystyle $\mathbf$ {$r}'}$이(가) 위치한$$ 환경에 따라 달라진다.^[24]

두 지점이 구 > , >) 밖에 있을 (r > a ${\displaystyle r>a,r'>a}:$

${\displaystyle {\hat {\bf {G}}}^{00}({\mathbf {r} ,\mathbf {r} ',k,k_{1}})={\hat {\bf {G}}}^{0}({\mathbf {r} ,\mathbf {r} ',k})+{\frac {ik}{4\pi }}\sum _{n=1}^{\infty }\sum _{m=0}^{n}(2-\delta _{m,0}){\frac {2n+1}{n(n+1)}}{\frac {(n-m)!}{{n+m!}}}\cdot }$

${\displaystyle \cdot {\Bigl (}a_{n}^{(0)}(\omega )(\mathbf {M} _{^{e}_{o}mn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {M} }_{^{e}_{o}mn}^{(3)}[k,\mathbf {r} '])+b_{n}^{(0)}(\omega )({\mathbf {N} }_{^{e}_{o}mn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {N} }_{^{e}_{o}mn}^{(3)}[k,\mathbf {r} ']){\Bigr )}}$

계수가 다음과 같은 경우:

${\displaystyle a_{n}^{(0)}(\omega )={\frac {\mu /\mu _{1}\left[\rho _{1}j_{n}(\rho _{1})\right]'j_{n}(\rho )-\left[\rho j_{n}(\rho )\right]'j_{n}(\rho _{1})}{\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu /\mu _{1}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}},}$

${\displaystyle b_{n}^{(0)}(\omega )={\frac {n^{2}\mu _{1}/\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'j_{n}(\rho )-n_{1}^{2}\left[\rho j_{n}(\rho )\right]'j_{n}(\rho _{1})}{n_{1}^{2}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-n^{2}\mu _{1}/\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}}.}$

두 점이 모두 구 내부에 있을 때(< , < ${\displaystyle r<a,r'>$) :

${\displaystyle {\hat {\bf {G}}}^{11}({\mathbf {r} ,\mathbf {r} ',k,k_{1}})={\hat {\bf {G}}}^{0}({\mathbf {r} ,\mathbf {r} ',k_{1}})+{\frac {ik_{1}}{4\pi }}\sum _{n=1}^{\infty }\sum _{m=0}^{n}(2-\delta _{m,0}){\frac {2n+1}{n(n+1)}}{\frac {(n-m)!}{{n+m!}}}\cdot }$

${\displaystyle \cdot {\Bigl (}c_{n}^{(1)}(\omega )(\mathbf {M} _{^{e}_{o}mn}^{(1)}[k_{1},\mathbf {r} ]\otimes {\mathbf {M} }_{^{e}_{o}mn}^{(1)}[k_{1},\mathbf {r} '])+d_{n}^{(1)}(\omega )({\mathbf {N} }_{^{e}_{o}mn}^{(1)}[k_{1},\mathbf {r} ]\otimes {\mathbf {N} }_{^{e}_{o}mn}^{(1)}[k_{1},\mathbf {r} ']){\Bigr )},}$

계수:

${\displaystyle c_{n}^{(1)}(\omega )={\frac {\mu _{1}/\mu \left[\rho h_{n}(\rho )\right]'h_{n}(\rho _{1})-\left[\rho _{1}h_{n}(\rho _{1})\right]'h_{n}(\rho )}{\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )-\mu _{1}/\mu \left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})}},}$

${\displaystyle d_{n}^{(1)}(\omega )={\frac {n_{1}^{2}\mu /\mu _{1}\left[\rho h_{n}(\rho )\right]'h_{n}(\rho _{1})-n^{2}\left[\rho _{1}h_{n}(\rho _{1})\right]'h_{n}(\rho )}{n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )-n_{1}^{2}\mu /\mu _{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})}}.}$

소스는 구체 내부에 있고, 관측점은 외부(r> ,< ${\displaystyle r>a,r'<a}$ ):

${\displaystyle {\hat {\bf {G}}}^{01}({\mathbf {r} ,\mathbf {r} ',k,k_{1}})={\frac {ik_{1}}{4\pi }}\sum _{n=1}^{\infty }\sum _{m=0}^{n}(2-\delta _{m,0}){\frac {2n+1}{n(n+1)}}{\frac {(n-m)!}{{n+m!}}}\cdot }$

${\displaystyle \cdot {\Bigl (}a_{n}^{(1)}(\omega )(\mathbf {M} _{^{e}_{o}mn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {M} }_{^{e}_{o}mn}^{(1)}[k_{1},\mathbf {r} '])+b_{n}^{(1)}(\omega )({\mathbf {N} }_{^{e}_{o}mn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {N} }_{^{e}_{o}mn}^{(1)}[k_{1},\mathbf {r} ']){\Bigr )}}$

계수:

${\displaystyle a_{n}^{(1)}(\omega )={\frac {\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho _{1})-\left[\rho _{1}h_{n}(\rho _{1})\right]'j_{n}(\rho _{1})}{\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )-\mu _{1}/\mu \left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})}},}$

${\displaystyle b_{n}^{(1)}(\omega )={\frac {nn_{1}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho _{1})-nn_{1}\left[\rho _{1}h_{n}(\rho _{1})\right]'j_{n}(\rho _{1})}{n^{2}\mu _{1}/\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )-n_{1}^{2}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})}}.}$

소스가 구 밖에 있고 관찰 지점이 내부에 있다$($ <$a,r>a$

${\displaystyle {\hat {\bf {G}}}^{10}({\mathbf {r} ,\mathbf {r} ',k,k_{1}})={\frac {ik}{4\pi }}\sum _{n=1}^{\infty }\sum _{m=0}^{n}(2-\delta _{m,0}){\frac {2n+1}{n(n+1)}}{\frac {(n-m)!}{{n+m!}}}\cdot }$

${\displaystyle \cdot {\Bigl (}c_{n}^{(0)}(\omega )(\mathbf {M} _{^{e}_{o}mn}^{(1)}[k,\mathbf {r} ]\otimes {\mathbf {M} }_{^{e}_{o}mn}^{(3)}[k_{1},\mathbf {r} '])+d_{n}^{(0)}(\omega )({\mathbf {N} }_{^{e}_{o}mn}^{(1)}[k,\mathbf {r} ]\otimes {\mathbf {N} }_{^{e}_{o}mn}^{(3)}[k_{1},\mathbf {r} ']){\Bigr )}}$

계수:

${\displaystyle c_{n}^{(0)}(\omega )={\frac {\left[\rho h_{n}(\rho )\right]'j_{n}(\rho )-\left[\rho j_{n}(\rho )\right]'h_{n}(\rho )}{\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu /\mu _{1}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}},}$

${\displaystyle d_{n}^{(0)}(\omega )={\frac {nn_{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho )-nn_{1}\left[\rho j_{n}(\rho )\right]'h_{n}(\rho )}{n_{1}^{2}\mu /\mu _{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]'j_{n}(\rho )}}.}$

계산 코드

Mie 솔루션은 Fortran, MATLAB, Mathematica와 같은 다른 컴퓨터 언어로 작성된 많은 프로그램으로 구현된다. 이 솔루션은 무한 시리즈를 해결하며, 산란 위상 함수, 소멸, 산란 및 흡수 효율과 비대칭 파라미터 또는 방사선 토크와 같은 기타 파라미터의 계산을 출력물로 제공한다. "Mie 솔루션"이라는 용어의 현재 용어는 맥스웰 방정식의 솔루션에 대한 일련의 근사치를 나타낸다. 그러한 해결책을 허용하는 몇 가지 알려진 물체가 있다: 구체, 동심원구, 무한원통, 구들의 군집과 실린더의 군집. 타원성 입자에 의한 산란용액도 알려져 있다. 이러한 전문 솔루션을 구현하는 코드 목록은 다음과 같다.

• 구에 의한 전자기 산란 코드 - 단일 구, 코팅된 구, 다층 구 및 구 군집을 위한 솔루션
• 실린더별 전자기 산란 코드 - 단일 실린더, 다층 실린더 및 실린더 군집용 솔루션.

보다 일반적인 형태의 입자를 처리할 수 있는 일반화는 T-매트릭스 방식으로, 맥스웰 방정식의 용액에 대한 직렬 근사치에 의존하기도 한다.

다른 코드 및 계산기는 외부 링크를 참조하십시오.

적용들

미에 이론은 기상 광학에서 매우 중요하다. 단결 순서와 더 큰 순서의 직경 대 파장 비율이 연무와 구름 산란과 관련된 많은 문제에서 특징적이다. 광학적 산란 측정에 의한 입자의 특성화에 추가 적용이 있다. 미에 용액은 우유, 생물학적 조직, 라텍스 페인트와 같은 일반적인 물질의 외관을 이해하는 데도 중요하다.

대기과학

미에 산란은 대기 먼지 직경이 산란된 빛의 파장과 비슷하거나 클 때 발생한다. 먼지, 꽃가루, 연기, 구름을 형성하는 미세한 물방울은 미에가 산란하는 흔한 원인이다. 미에 산란은 대기의 낮은 부분에서 주로 발생하는데, 더 큰 입자가 더 풍부하고, 흐린 조건에서 지배한다.

암 검진 및 검진

미에 이론은 각도로 분해된 저공진성 간섭계를 사용하여 조직에서 나오는 산란된 빛이 건강한 세포핵에 해당하는지 또는 암세포핵에 해당하는지를 판별하는 데 이용되어 왔다.

임상실험실 분석

미에 이론은 혈장 기반 검사의 응용에 있어서 중심 원리로, 다양한 혈장 단백질을 측정하는 의학에서 널리 사용된다. 혈장 단백질의 광범위한 배열을 감지하고 족벌법으로 계량화할 수 있다.

자분입자

자기구에는 여러 가지 특이한 전자기 산란 효과가 발생한다. 상대적 허용률이 투과도와 같을 때, 백스캐터 이득은 0이다. 또한 산란 방사선은 입사 방사선과 같은 의미로 극성을 띤다. 소입자(또는 장파장) 한계에서 전방 산란 제로, 다른 방향으로 산란 방사선의 완전한 양극화, 후방 산란에 대한 전방 산란 비대칭의 조건이 발생할 수 있다. 소입자 한계의 특별한 경우는 완전한 양극화와 전방-대-후방사선 비대칭의 흥미로운 특별한 경우를 제공한다.^[25]

메타물질

미에 이론은 메타 물질을 설계하는 데 이용되어 왔다. 일반적으로 금속 또는 비금속 혼합물의 3차원 복합 재료로 구성되며 주기적으로 또는 저주파율 매트릭스에 무작위로 내장된다. 그러한 계획에서 음의 구성 매개변수는 포함물의 미에 공진 주위에 나타나도록 설계된다. 음의 유효 허용도는 미에 전기 쌍극자 산란계수의 공진 주위로 설계되는 반면, 음의 유효 투과성은 미에 자성 쌍극자 산란계수의 공진 주위로 설계된다.링 계수 및 이중 부성 물질(DNG)은 미에 전기 및 자기 이중극자 산란 계수의 공명 중첩을 중심으로 설계된다. 입자는 보통 다음과 같은 조합을 갖는다.

1. 상대적 허용성 및 투과성 값이 한 개보다 훨씬 크고 서로 가까운 자기 계통 입자 한 세트
2. 두 개의 서로 다른 유전체 입자(유속성은 동일하지만 크기는 다름)
3. 크기가 동일하지만 순발성이 다른 두 개의 다른 유전체 입자

이론적으로 미에 이론에 의해 분석된 입자들은 일반적으로 구형이지만, 실제로는 입자들은 제작이 용이하도록 정육면체나 실린더로 제작된다. 균질화의 형태에서 격자 상수는 영업 파장보다 작다고 말할 수 있는 기준을 만족시키기 위하여,, 유전 입자들의 상대적인 유전율은 1보다, 예를 들어 ε r>78(38){\displaystyle \varepsilon_{\text{r}}>78(38)}부정적인 효과적인 파마를 달성하기 위해 커야 한다.ittiv이티(가변성)^[26][27][28]

입자 크기 조정

미에 이론은 레이저 회절 분석에서 입자 크기 조정 효과를 검사하기 위해 종종 적용된다.^[29] 1970년대 초기 컴퓨터는 프라운호퍼 근사치를 보다 단순한 것으로만 회절 데이터를 계산할 수 있었던 반면, 미에는 1990년대 이후 널리 사용되고 있으며 가이드라인 ISO 13320:2009에서 50마이크로미터 미만의 입자에 대해 공식적으로 권장하고 있다.^[30]

미에 이론은 오염된 물에서 기름 농도의 검출에 이용되어 왔다.^[31][32]

미에 산란은 물속의^[33][34][35] 공기 방울을 단일 소놀루민으로 크기화하는 일차적인 방법이며, 주변 물질이 본질적으로 비흡수적인 한 물질의 구멍뿐만 아니라 물질의 입자에도 유효하다.

기생충학

그것은 또한 말라리아의 특히 병원성 형태인 플라스모듐 팔시파룸의 구조를 연구하는 데 사용되었다.^[36]

확장

1986년 P. A. Bobert와 J. Vlieger는 Mie 모델을 확장하여 평평한 표면에 배치된 균일한 매질에서 구체에 의한 산란을 계산하였다. 미에 모델처럼 확장형 모델을 입사광의 파장에 가까운 반경을 가진 구에 적용할 수 있다.^[37] 밥버트-블리에거(BV) 모델을 구현하는 C++ 코드가 있다.^[38] 최근의 발전은 타원체 산란과 관련이 있다.^[39][40][41] 현대 연구는 잘 알려진 레일리 연구에 들어간다.^[42]

참고 항목

• 계산 전자석학
• 입자에 의한 빛 산란
• 대기 복사 전송 코드 목록
• 구에 의한 전자기 산란 코드
• 물과 얼음의 광학적 특성

참조

추가 읽기

• Kerker, M. (1969). The scattering of light and other electromagnetic radiation. New York: Academic.
• Barber, P. W.; Hill, S. S. (1990). Light scattering by particles: Computational methods. Singapore: World Scientific. ISBN 978-9971-5-0813-5.
• Mishchenko, M.; Travis, L.; Lacis, A. (2002). Scattering, Absorption, and Emission of Light by Small Particles. New York: Cambridge University Press. ISBN 978-0-521-78252-4.
• Frisvad, J.; Christensen, N.; Jensen, H. (2007). "Computing the Scattering Properties of Participating Media using Lorenz-Mie Theory" (PDF). ACM Transactions on Graphics. 26 (3): 60. doi:10.1145/1276377.1276452.
• Wriedt, Thomas (2008). "Mie theory 1908, on the mobile phone 2008". Journal of Quantitative Spectroscopy & Radiative Transfer. 109 (8): 1543–1548. Bibcode:2008JQSRT.109.1543W. doi:10.1016/j.jqsrt.2008.01.009.
• Lorenz, Ludvig (1890). "Lysbevægelsen i og uden for en af plane Lysbølger belyst Kugle". Det Kongelige Danske Videnskabernes Selskabs Skrifter. 6 (6): 1–62.

외부 링크

• JMIE(2D C++ 코드: 무한 실린더 주위의 분석 필드 계산, Jeffrey M. McMahon에서 개발)
• SPATLIB: 광 산란 코드 모음
• www.T-Matrix.de. FORTRAN, C++, IDL, Pascal, Mathematica 및 Mathcad에서 Mie 솔루션 구현
• 스캣랩. Windows용 산란 소프트웨어.
• Python 래퍼가 포함된 오픈 소스 C++ Mie 솔루션 패키지인 Scattnlay. 다층 구를 위한 원거리 및 근거리 시뮬레이션 결과 제공.
• STRATIFY MatLab 코드는 선원이 점 쌍극자 및 평면 파형인 경우 다층 구에서 산란하는 코드. arXiv:2006.06512의 설명
• 온라인 Mie 산란 계산기는 벌크, 코어 쉘, 다층 구에 대한 시뮬레이션 결과를 제공한다. 재료 매개변수는 refractiveindex.info 웹사이트의 nk-data 파일에 대한 링크를 통해 설정할 수 있다. 소스 코드는 GitHub에서 자유롭게 사용할 수 있는 Scattnlay 프로젝트의 일부다.
• 온라인 Mie 솔루션 계산기는 독일어와 영어로 된 문서와 함께 사용할 수 있다.
• 온라인 Mie 산란 계산기는 다양한 매개변수에 걸쳐 아름다운 그래프를 만든다.
• PHP에 작성된 ppMie 온라인 미에 산란 계산기
• 미에 공명은 빛의 확산과 무작위 레이싱을 매개했다.
• 구면 입자에 대한 미에 용액.
• 파이미스카트, 파이톤으로 작성된 미에 솔루션 패키지.
• Python 래퍼가 포함된 오픈 소스 C++ Mie 솔루션 패키지인 PyMieForAll.