런던 분산군

아르곤디머의 상호작용 에너지.장거리 구간은 런던 분산군 때문이다.

힘의(LDF, 또한 분산 힘, 런던, 순간 dipole–induced 쌍극자 힘으로, 밴 데스 발스 힘으로 유도 쌍극자 bonds[1]거나 느슨하게 변동하는 알려진)는 원자와 정상적으로 전기적으로 대칭 분자 사이에 연기 런던 분산 힘, 즉 이 전자들은 대칭적으로여 배부한다. 실체핵을 ^[2]찌르다그들은 반데르발스 군대의 일부입니다.LDF는 독일 물리학자 프리츠 런던의 이름을 따왔다.

서론

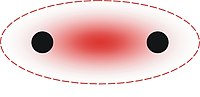
원자나 분자 주위의 전자 분포는 시간의 변동을 겪는다.이러한 변동은 근처의 다른 원자와 분자에 의해 감지되는 순간적인 전기장을 생성하며, 이는 다시 그들 자신의 전자의 공간 분포를 조절합니다.순효과는 한 원자의 전자 위치 변동은 다른 원자의 전자 재분배를 유도하여 전자 운동이 상관관계가 되도록 하는 것입니다.상세한 이론은 양자역학적 설명을 필요로 하지만(분산력에 대한 양자역학 이론 참조), 그 효과는 종종 (진공에 의해 분리될 때) 서로를 끌어당기는 순간 쌍극자의 형성으로 설명된다.런던 분산력의 크기는 흔히 Hamaker 상수(일반적으로 A로 표시됨)라고 불리는 단일 매개변수로 설명된다.빛의 파장보다 더 가까이 위치한 원자의 경우, 상호작용은 본질적으로 순간적이며 "비거치" Hamaker 상수로 설명됩니다.더 멀리 떨어져 있는 실체의 경우, 한 원자의 변동이 두 번째 원자에서 느껴질 때까지의 유한한 시간("retarded")은 "retarded" Hamaker ^[3]^[4]상수를 사용해야 한다.

반면 개별 원자와 분자 사이의 런던 분산력고 빠르게 분리(R)과 1R6{\displaystyle{\frac{1}{R^{6}처럼}을 감소시켜}}가 약해서 응집 물질(액체와 고체)에, 그 영향 materials,[5]의 볼륨이나 안에 유기 분자, 그러한 런던 사이는 끝나는 누적된다. 경멸하다이온 힘은 부피 고체와 액체에서 상당히 강할 수 있으며 거리에 따라 훨씬 더 천천히 붕괴된다.예를 들어, 두 벌크 고체 사이의 단위 면적당 총 힘은 1 ${\frac {1}{R^{3}}}$ ${\frac {1}{R^{3}}}$ 합니다(\ $displaystyle\frac$ {1 $}{R^{$ 3 ${\frac {1}{R^{3}}}$ ^[6]}}}). 여기서 R은 둘 사이의 간격입니다.런던 분산력의 영향은 탄화수소와 브롬(상온에서 브라질 액체)이나_2, 요오드(상온에서_2, 고체)와 같은 대칭성이 높은 분자와 같이 매우 비극적인(예를 들어 이온 결합이 결여된) 시스템에서 가장 뚜렷하다.탄화수소 및 왁스의 경우, 분산력은 기체상에서 액체상 또는 고체상으로 응축을 일으키기에 충분합니다.예를 들어 탄화수소 결정의 승화열은 분산 상호작용을 반영한다.산소와 질소가스를 액상으로 액화하는 것 또한 런던의 매력적인 분산력에 의해 지배된다.

원자/분자가 진공이 아닌 제3의 매질로 분리되면 상황은 더욱 복잡해집니다.수용액에서는 분극성 용제 분자와의 경쟁으로 인해 원자 또는 분자 간의 분산력의 효과가 종종 덜 두드러진다.즉, 한 원자 또는 분자의 순간적인 변동은 용매(물)와 다른 분자에 의해 모두 느껴집니다.

크고 무거운 원자와 분자는 작고 가벼운 ^[7]원자보다 강한 분산력을 보인다.이것은 더 크고 더 분산된 전자 구름을 가진 분자의 분극성이 증가했기 때문입니다.분극성은 전자가 얼마나 쉽게 재배포될 수 있는지를 나타내는 척도이다. 분극성이 크면 전자가 더 쉽게 재배포된다는 것을 의미한다.이러한 경향은 할로겐(가장 작은 것부터 가장 큰 것까지₂: F, Cl₂, Br₂, I₂)으로 대표된다.분산 흡인력의 증가는 RF, RCl, RBr, RI(최소에서 최대) 순서로 유기 분자 내부와 사이에서 발생하거나 분극성이 더 높은 헤테로아톰을 ^[8]사용하여 발생합니다.불소와 염소는 상온의 기체, 브롬은 액체, 요오드는 고체입니다.런던의 힘은 전자의 움직임에서 발생하는 것으로 생각된다.

양자역학 이론

1930년 ^[9]^[10]^[11]프리츠 런던은 귀가스 원자 사이의 흡인력에 대해 처음으로 설명했다.그는 2차 섭동 이론에 기초한 양자역학 이론을 사용했다.섭동은 두 부분(아톰 또는 분자)의 전자와 핵 사이의 쿨롱 상호작용 때문이다.상호작용 에너지의 2차 섭동 표현식은 합계를 포함한다.이 합계에 나타나는 상태는 단량체의 자극된 전자 상태의 단순한 산물이다.따라서 전자상태의 분자간 반대칭은 포함되지 않으며 파울리 배타원리는 부분적으로만 충족된다.

런던은 ${\frac {1}{R}}$ 의 테일러 시리즈 확장을 $1R$ 로 작성했다 ${\frac {1}{R}}$ $R$ 서 $R은$ 핵물질 중심 사이의 거리이다 $.$

이 시리즈의 항은 각 단량체에 하나씩, 상호작용하는 두 다중극의 에너지로 간주될 수 있기 때문에 이 팽창을 다중극 팽창이라고 한다.V의 다극 확장 형식을 2차 에너지로 치환하면 순간 다중극 간의 상호작용을 설명하는 표현과 유사한 표현이 생성된다(위의 정성적 설명 참조).또한 알브레히트 언숄드(Albrecht $\alpha '$ Unsöld)의 이름을 딴 근사치를 도입하여 분극률 $\alpha '$ α ${\$ \ $displaystyle \$ alpha $\alpha '$ ' 및 이온화 $에너지$ I \ $displaystyle$ I $I$ (옛 용어: 이온화 퍼텐셜s)의 관점에서 런던 분산을 설명해야 한다.

이 방법으로 분산 $E_{AB}^{\rm {disp}}$ $E_{AB}^{\rm {disp}}$ $E_{AB}^{\rm {disp}}$ $E_{AB}^{\rm {disp}}$ s $\$ E_ ${$ 에 대한 근사치를 구한다. $AB}^{\rm {disp}$ 은 $E_{AB}^{\rm disp}$ 2개의 $원자$ A(\ $displaystyle$ A $)$ 와 $a$ B(\ $displaystyle$ B $B$ 사이에 있으며, $\alpha '_{A}$ 서 $\alpha '_{A}$ A $′$ \ $displaystyle$ $\alpha$ $'_{A}$ 와 $\alpha '_{A}$ $\alpha '_{B}$ $\alpha '_{B}$ ${\$ \ $displaystyle$ \alpha ' $_{B})$ 는 $\displaystyle \alpha '_{B}$ 각 원자의 분극률 부피이다. $I_{A}$ $($ I_ ${A})$ 와 $I_{A}$ $I_{B}$ B $($ I_ ${B})$ 는 $I_{B}$ 원자의 첫 번째 이온화 현상이며 $,$ $R$ ( $표시 스타일$ R $)$ 은 $r$ 분자간 거리이다.

$E_{AB}^{\rm {disp}}\약 -{3 \over 2){I_{A}I_{B}\over I_{A}+I_{B}}{\alpha '_{A}\alpha '_{B}\over {R^{6}}}}}$

이 최종 런던 방정식은 순간 쌍극자를 포함하지 않는다(분자 쌍극자 참조).그러한 두 쌍극자 사이의 상호작용으로서의 분산력의 "해명"은 런던이 적절한 양자역학 이론에 도달한 후에 발명되었다.이^[12] 권위 있는 작품은 순간 쌍극자^[13] 모델에 대한 비판과 분자간 힘의 이론에 대한 현대적이고 철저한 설명을 포함하고 있다.

런던 이론은 빛의 분산에 대한 양자역학 이론과 매우 유사하며, 이것이 런던이 "분산 효과"라는 문구를 만든 이유입니다.물리학에서 "분산"이라는 용어는 주파수에 따른 양의 변동을 나타내며, 이는 런던 분산의 경우 전자의 변동이다.

상대 진도

분산력은 물과 같이 작고 극성이 강한 분자를 제외하고 원자와 분자 사이의 3개의 반데르발스 힘(방향, 유도, 분산)에 대해 지배적이다.총 분자간 상호작용 에너지에 대한 분산의 기여는 다음과 같다.^[14]

총 분자간 상호작용 에너지에 대한 분산의 기여
분자쌍	상호작용 총 에너지의 %
니네	100
CH₄-CH₄	100
HCl-HCl	86
HBr-HBr	96
하이하이	99
CH₃Cl-CH₃Cl	68
NH₃-NH₃	57
호호₂₂	24
HCL-HI	96
호치₂₄	87

「」를 참조해 주세요.

레퍼런스

^ Callister, William (December 5, 2000). Fundamentals of Materials Science and Engineering: An Interactive e . Text. John Wiley & Sons, Inc. p. 25. ISBN 0-471-39551-X.
^ Callister, William D., Jr.; Callister, William D., Jr. (2001). Fundamentals of materials science and engineering : an interactive etext. New York: Wiley. ISBN 0-471-39551-X. OCLC 45162154.{{cite book}}: CS1 maint: 여러 이름: 작성자 목록(링크)
^ Israelachvili, Jacob N. (2011), "Interactions of Biological Membranes and Structures", Intermolecular and Surface Forces, Elsevier, pp. 577–616, doi:10.1016/b978-0-12-375182-9.10021-1, ISBN 978-0-12-375182-9
^ Gelardi, G.; Flatt, R.J. (2016), "Working mechanisms of water reducers and superplasticizers", Science and Technology of Concrete Admixtures, Elsevier, pp. 257–278, doi:10.1016/b978-0-08-100693-1.00011-4, ISBN 978-0-08-100693-1
^ Wagner, J.P.; Schreiner, P.R. (2015), "London dispersion in molecular chemistry — reconsidering steric effects", Angewandte Chemie International Edition, Wiley, 54 (42): 12274–12296, doi:10.1002/anie.201503476, PMID 26262562
^ Karlström, Gunnar; Jönsson, Bo (6 February 2013). "Intermolecular interactions" (PDF). Theoretical chemistry – Lund University. p. 45. Archived (PDF) from the original on 18 September 2020. Retrieved 18 September 2020.
^ "London Dispersion Forces". Retrieved May 24, 2019.
^ Schneider, Hans-Jörg 분산 상호작용 솔루션 복합체에서의 분산 상호작용 Acc. Chem. Res 2015, 48, 1815–1822. [1]
^ R. Eisenschitz & F. London (1930), "Über das Verhältnis der van der Waalsschen Kräfte zu den homöopolaren Bindungskräften", Zeitschrift für Physik, 60 (7–8): 491–527, Bibcode:1930ZPhy...60..491E, doi:10.1007/BF01341258, S2CID 125644826
^ 런던, F.(1930년),"벳술 Theorie Systematik der Molekularkräfte und", Zeitschrift für Physik, 63(3–4):245Bibcode:1930ZPhy...63..245L, doi:10.1007/BF01421741, S2CID 123122363.H에 영어 번역본Hettema,(2000년), 양자 화학, 클래식 과학 논문, 싱가포르:.세계 과학, 아이 에스비엔 981-02-2771-X, 온라인 컴퓨터 도서관 센터 898989103, OL9194584M는 파, 로버트 G.(2001년),"양자 화학:클래식 과학 논문", 물리학 오늘날, 54(6):63–64, Bibcode:2001PhT....54f.에서 재검토된다.63H, doi:10.1063/1.1387598
^ F. London (1937), "The general theory of molecular forces", Transactions of the Faraday Society, 33: 8–26, doi:10.1039/tf937330008b
^ J. O. Hirschfelder; C. F. Curtiss & R. B. Bird (1954), Molecular Theory of Gases and Liquids, New York: Wiley
^ A. J. Stone (1996), The Theory of Intermolecular Forces, Oxford: Clarendon Press
^ Jacob Israelachvili (1992), Intermolecular and Surface Forces (2nd ed.), Academic Press

[1] Callister, William (December 5, 2000). Fundamentals of Materials Science and Engineering: An Interactive e . Text. John Wiley & Sons, Inc. p. 25. ISBN 0-471-39551-X.

[2] Callister, William D., Jr.; Callister, William D., Jr. (2001). Fundamentals of materials science and engineering : an interactive etext. New York: Wiley. ISBN 0-471-39551-X. OCLC 45162154.{{cite book}}: CS1 maint: 여러 이름: 작성자 목록(링크)

[3] Israelachvili, Jacob N. (2011), "Interactions of Biological Membranes and Structures", Intermolecular and Surface Forces, Elsevier, pp. 577–616, doi:10.1016/b978-0-12-375182-9.10021-1, ISBN 978-0-12-375182-9

[4] Gelardi, G.; Flatt, R.J. (2016), "Working mechanisms of water reducers and superplasticizers", Science and Technology of Concrete Admixtures, Elsevier, pp. 257–278, doi:10.1016/b978-0-08-100693-1.00011-4, ISBN 978-0-08-100693-1

[5] Wagner, J.P.; Schreiner, P.R. (2015), "London dispersion in molecular chemistry — reconsidering steric effects", Angewandte Chemie International Edition, Wiley, 54 (42): 12274–12296, doi:10.1002/anie.201503476, PMID 26262562

[6] Karlström, Gunnar; Jönsson, Bo (6 February 2013). "Intermolecular interactions" (PDF). Theoretical chemistry – Lund University. p. 45. Archived (PDF) from the original on 18 September 2020. Retrieved 18 September 2020.

[7] "London Dispersion Forces". Retrieved May 24, 2019.

[8] Schneider, Hans-Jörg 분산 상호작용 솔루션 복합체에서의 분산 상호작용 Acc. Chem. Res 2015, 48, 1815–1822. [1]

[9] R. Eisenschitz & F. London (1930), "Über das Verhältnis der van der Waalsschen Kräfte zu den homöopolaren Bindungskräften", Zeitschrift für Physik, 60 (7–8): 491–527, Bibcode:1930ZPhy...60..491E, doi:10.1007/BF01341258, S2CID 125644826

[10] 런던, F.(1930년),"벳술 Theorie Systematik der Molekularkräfte und", Zeitschrift für Physik, 63(3–4):245Bibcode:1930ZPhy...63..245L, doi:10.1007/BF01421741, S2CID 123122363.H에 영어 번역본Hettema,(2000년), 양자 화학, 클래식 과학 논문, 싱가포르:.세계 과학, 아이 에스비엔 981-02-2771-X, 온라인 컴퓨터 도서관 센터 898989103, OL9194584M는 파, 로버트 G.(2001년),"양자 화학:클래식 과학 논문", 물리학 오늘날, 54(6):63–64, Bibcode:2001PhT....54f.에서 재검토된다.63H, doi:10.1063/1.1387598

[11] F. London (1937), "The general theory of molecular forces", Transactions of the Faraday Society, 33: 8–26, doi:10.1039/tf937330008b

[12] J. O. Hirschfelder; C. F. Curtiss & R. B. Bird (1954), Molecular Theory of Gases and Liquids, New York: Wiley

[13] A. J. Stone (1996), The Theory of Intermolecular Forces, Oxford: Clarendon Press

[14] Jacob Israelachvili (1992), Intermolecular and Surface Forces (2nd ed.), Academic Press

[2]

[3]

[4]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

Search

런던 분산군

네임스페이스

더

목차

서론

양자역학 이론

상대 진도

「」를 참조해 주세요.

레퍼런스

Search

런던 분산군

서론

양자역학 이론

상대 진도

「 」를 참조해 주세요.

레퍼런스

「」를 참조해 주세요.