렉셀 정리

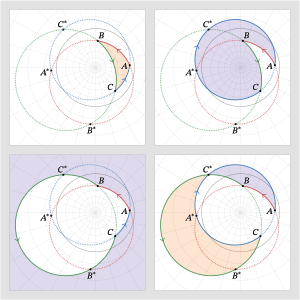
구면 기하학에서, 렉셀의 정리는 고정 밑면에 동일한 표면적을 가진 모든 구면 삼각형이 다른 두 꼭짓점에 반대되는 두 점을 통과하는 렉셀의 원 또는 렉셀의 ^[1]궤적이라고 불리는 작은 원 위에 정점을 가지고 있다고 주장합니다.

이 정리는 1777년에 발표된 논문에서 삼각법 증명과 기하학적 ^[2]증명을 모두 포함한 논문을 발표한 안데르스 요한 렉셀의 이름을 따서 명명되었습니다.렉셀의 동료인 레온하르트 오일러는 1778년에 또 다른 증명을 썼고, 다른 ^[3]사람들 중에서도 Adrien-Marie Legendre (1800년), Jakob Steiner (1827년), Carl Friedrich Gauss (1841년), Paul Serre (1855년), Joseph-Emile Barbier (1864년)에 다양한 증명이 작성되었습니다.

이 정리는 유클리드 원소 제1권의 명제 37과 39의 유사체로, 고정 기저 위에 동일한 면적을 가진 모든 평면 삼각형이 ^[4]기저와 평행한 직선 위에 정점을 가지고 있음을 증명합니다.정점이 하이퍼 사이클 위에 있는 쌍곡선 삼각형에 대해서도 유사한 정리가 증명될 수 있습니다.

진술

고정 기저 AB가 주어졌을 때, 구면에 큰 원의 호가 있고, 큰 원 AB의 같은 쪽에 있는 두 개의 정점 C와 X가 주어졌을 때, 렉셀의 정리는 구형 삼각형의 표면적이 △ B C의 표면적과 같다고 주장한다$A$$$${\displaystyle {\ast }^{}}$ \ $displaystyle$ A$$$^{*}$와 B$$$∗$ {\ $displaystyle$ B^{*}가$$ 각각 A$$$$\ $displaystyle$A$^{*}$와 B {\ $displaystyle$B$^{*}$의 $반대{\displaystyle }$ 지점인 $작은{\displaystyle {}^{}}$ 원 호 B$∗$ $^{*}\!,}$에 X가 $있는$ $경우$에만$$aystyle \ $triangle$ ABC$$$.$

삼각형의 면적에 대한 평면 ${\displaystyle \text{공식}}$ 영역 ${\displaystyle =}$ ${\displaystyle \text{12}}$ base $⋅$ $({$text${area$}}={$tftfrac{1}{2}}\,{\text{base}\cdot{text{height}})$로서,삼각형의 구면 초과 δ는 기저 c{displaystyle c}(호 A B의 각 길이)와 "높이" h c{{c}(평행한 작은 원 A δ B δ C와 B C 사이의 각 거리)로 계산할 수 있다 $$):^[5]

$디스플레이 스타일 \sin{tfrac{1}{2}}\varepsilon =\tan{tfrac{1}{2}}c\,\tan{tfrac{1}{2}h_{c}}$

구면의 반지름보다 훨씬 작은 삼각형의 한계에서 이는 평면 공식으로 감소합니다.

$작은$ $원{\displaystyle {}^{}}$ A ${\displaystyle {\ast }^{}}$ ${\displaystyle {}^{}{}^{}}$$$${\displaystyle {\ast }^{}}$$$ {\$displaystyle$ $A$$^{*}B^{*}$$C{\displaystyle }$$$및$$ ${\displaystyle {}^{}}$ $∗$ {{\$displaystyle$ABC$^{*}}$는 각각 큰 $원{\displaystyle }$를 ${\displaystyle \frac{12}{}˚}$ ${\displaystyle 각도}$로 교차합니다$.$

교정쇄

렉셀의 정리를 증명하는 몇 가지 방법이 있으며, 각각 관련된 관계의 다른 측면을 조명합니다.

이등변 삼각형

렉셀의 1777년 기하학적 증명의 주요 아이디어는 외젠 카탈루냐 (1843년), 로버트 알라디체 (1883년), 자크 아다마르 (1901년), 앙투안 고브 (1922년),그리고 마에하라 히로시 (1999) – 삼각형 △ A ∗ B ∗ C \displaystyle \displaystyle A^{*}B^{*}C를 원주 중심 P에서 공통 정점을 갖는 세 개의 이등변 삼각형으로 분할한다 $$ 그리고 삼각형$ABC$의 구형 초과$\delta {\displaystyle }$({$displaystyle \$$varepsilon$$})$를 찾기 위해 각도를 쫓습니다$.$그림에서$$, A$지점$과$B{\displaystyle }$ $지점$은 구의 반대편에 있습니다. 그래서 우리는 그들의 대척점과 모든 $Lexell$의 $원{\displaystyle }$l을$$명확하게 볼 수 $있습니다.$

이등변 삼각형의 기저각 △ B ∗ CP (그림의 빨간색 부분), △ CA ∗ P (파란색 부분), △ A ∗ P (파란색 부분), {\ A ∗ P (파란색 부분)를 각각 α ^{*}, α \style \alpha \style \tyle β, 및 일부 \style \tyle \tyle \tyle \tyle \tyle \tyle \tyle \tyle \tyle \tyla \tyla \tyle \tyle \es ${displaystyle$P}가${\displaystyle \mathrm{}}$△ ${\displaystyle {}^{}{}^{}}$∗${\displaystyle {}^{}}$$B$ $∗$ ${\displaystyle {}^{}}$ {\$displaystyle$ \$displaystyle$$$A$^{*}$B$^\{*\}$$C$를 벗어나면 ${\displaystyle \alpha ,}$β, γ$$\$displaystyle$ \alpha$,\$displaystyle,\displaystyle$$$$} 중 하나가 음수가 됩니다.우리는 이러한 각도로 △ ABC의 내부 각도를 계산할 수 있다: γ A = β - γ \displaystyle A =\pi -\displaystyle -\displaysyle A π (γ B = \gangle A^{*}의 보충), 마찬가지로 γ B = γ -α - β, γ 및 α \style β \displaystyle C \displaystyle β \displaystyle β \displaystyle\displaystyle β$각도 C=\alpha +\lambda.}$

지라드의 정리에 따르면$,$△ $ABC$의 구면 $초과$는 다음과 같습니다$.$

$표시(\style\varepsilon &=\angle A+\angle B+\angle C-\pi \[3mu]&=(\pi -\alpha -\alpha )+(\alpha +\alpha )-\pi \[3mu]&=\pi -2\alpha.\end{aligned}}}$

만약 기저 AB가 고정되어 있다면, 렉셀 원의 같은 호 위에 있는 어떤 세 번째 꼭짓점 C에 대하여, P{displaystyle P} 점과 따라서 양 δ{displaystyle \displaystyle \displaysilon}은 변하지 않을 것이고, 따라서 △ BC의 초과 δ \displaystyle \varepsilon은 오직 δ에 의존한다$스타일 \timeout,}$도 마찬가지로 상수입니다.그리고 반대로$점{\displaystyle }$ $C$가 변경되었을 때$$$\epsilon {\displaystyle }$$${\$displaystyle$ \$varepsilon}$이 일정하게 유지된다면,$δ$ {\displaystyle$$$\delta}$이(가) 되어야 하며, $따라서{\displaystyle }$P {\$displaystyle$ P$}$이(가) 고정되어야 $하므로{\displaystyle }$C {\$displaystyle$ C$}$는 렉셀의 원에 남아 있어야 합니다.

순환 사각형

Jakob Steiner (1827)는 또한 Girard의 정리를 사용하여 Lexell과 유사한 스타일의 증명을 작성했지만, Lexell 원 안에 순환 사각형을 구성함으로써 삼각형 $△{\displaystyle \mathrm{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$ ${\displaystyle {}^{}}$ ∗ C$$\ $displaystyle$ \ displaystyle $A^{*}B^{*}C}$의 각도 불변량을 증명했습니다.구면 순환 사각형에서 서로 반대되는 각도의 쌍이 같은 ^[8][9]합을 갖는 특성을 사용합니다.

삼각형 △ AB C로 시작하여, △ A ∗ B ∗ C, {\displaystyle D}를 L의 다른 점으로 하고, 큰 원 B ∗ B ∗ B ！{\displaystyle C }에서 분리된 D {\displaystyle D}를 L의 다른 점으로 한다.} α 1 = ∠ CA ∗ B ∗, \displaystyle \alpha _{1}=\angle CA^{*}B^{*}\!,} β 1 = ∠ A ∗ C, \displaystyle \alpha _{1}=\angle A^{*}C, α 2 = ∠ B ∗ A ∗ D, \stystystyle \alpha ={{\angle B } β^{\angle} β^{D} β^{\d

사각형 ◻ A ∗ DB ∗ C \ square A^{*}DB^{*}C}가 주기적이기 때문에, 그 반대각의 각 쌍의 합은 ∠ C + ∠ D = α 1 + α 2 + β 1 + β 2, {\ displaystyle \angle C + \ α _ 1 + α 2 + β 1 + β 2, \ alpha 1 + β 2, 또는 β 1 - 1 β 2, 또는 β 1 - 1, 또는 - 1 - 2이다.${\displaystyle \alpha _{1}+\alpha _{1}-\angle C=\angle D-\alpha _{2}-\alpha _{2}.$$}$

지라드의 정리에 따르면,$△{\displaystyle \mathrm{}}$ $ABC$의 구형 초과 $({displaystyle$ $\varepsilon$$})$는

$표시(\style{aligned}\varepsilon &=\angle A+\angle B+\angle C-\[3mu]&(\pi -\alpha _{1})+(\pi -\alpha _{1})&=\pi -(\alpha _{1}+\angle C)[3mu - (\pi - {2})를 표시합니다.\end{aligned}}}$

수량${\displaystyle \mathrm{}\delta }$ ${\displaystyle {}_{}}$- ${\displaystyle {}_{}{}_{}}$2 - ${\displaystyle {\beta \mathrm{}}_{}}$2 \$displaystyle \angle D-\alpha$ _${2}-\beta$ _${2}$는${\displaystyle }$C의$선택$에 의존하지 않으므로 C$${\$displaystyle$ C$}$가${\displaystyle }$l$.{\displaystyle$ l$.}$의 동일한 호에 있는 다른 지점으로 $이동$할 때 불변하므로$\delta {\displaystyle }${$displaystyle \varepsilon}$도 불변합니다.

반대로, 만약 C{displaystyle C}가 변경되었지만 γ{displaystyle \varepsilon}가 불변이라면, 사각형 ◻ A γ DB^{\displaystyle \square A^{*}DB^{*}C}의 반대 각도는 동일한 합을 가질 것이며, 이는 C{displaystyle C}가 작은 원 A δ DB^{\}에 놓여 있음을 의미한다

구면 평행사변형

오일러는 1778년에 렉셀의 정리를 유클리드의 원소 I.35와 I.37의 증명과 비슷하게 증명했고, 빅토르-아메데 르베그는 1855년에 독립적으로 구면 평행사변형을 사용했습니다.그것들은 인접한 꼭짓점의 반대 쌍을 통과하는 평행한 작은 원을 가지고 있고 많은 면에서 유클리드 평행사변형과 유사합니다.그러나 유클리드의 증명과 비교할 때 한 가지 복잡한 점이 있습니다.구형 평행사변형의 네 변은 평행한 작은 원이 아니라 꼭짓점을 통과하는 대원호입니다.유클리드의 증명은 평면 ^[10]케이스에서 사라지는 큰 원과 작은 원 사이에 끼어 있는 작은 렌즈 모양 영역을 설명할 필요가 없습니다.

요소 I.35와 유사한 부제: 동일한 기준과 동일한 평행선 사이에 있는 두 개의 구면 평행도형은 동일한 면적을 갖습니다.

증명: ABC 1 D 1({displaystyle \square ABC_{1})과 ◻ ABC 2({2}D_{2})가 BC 1({displaystyle BC_{1}})의 중간점을 통과하는 대원 m("중간선")과 D 1({AD1})이 일치하는 구면 평행사변형이라고 하자BC 2D 2. {{displaystyle \square ABC_{2}D_{2}} F를 AD 2와 BC 1 사이의 교차점으로 합니다. {{displaystyle B_{1}} 중간선 M이 공유되기 때문에 두 상단면 C 1D는 동일한 C_1D_{1}와 C2D {{2} 위면 C1}$cell{\displaystyle }${\$displaystyle$ l$}$은$($는) 중심선에 평행하고 A({$displaystyle$ A$})$와 B$({displaystyle$ B$)$를 $통과$하는 작은 원 $l{\displaystyle {}^{}}$∗({\$displaystyle$ l$^{*})$에 대척점입니다.$}$

l{displaystyle l}의 두 호는 합동이고, D1 D2 ≅ C1 C2, \displaystyle D_{1} D_{2}\cong C_{1} C_{2}, 따라서 두 곡선 삼각형 △ BC1 C2 △ BC1 C2, d D1 D2, displaystyle AD{1}는 각각의 상단에 의해 경계를 이룬다.각 평행사변형은 삼각형 $△{\displaystyle \mathrm{}}$ $(표시$ 스타일 \displaystyle ABF$)$에 추가된 이러한 곡선 삼각형 중 하나와 곡선 삼각형 △ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {}_{}}$ F$(표시$ 스타일 \displaystyle $D_{2}C_{1}F)$를 잘라낸 각 상단과 $,$ {\$displaystyle$ l$,}$ 사이의$$ 합동 렌즈 모양 영역 중 하나로 구성됩니다.따라서 평행사변형은 동일한 면적을 갖습니다. (Elements와 마찬가지로 평행사변형이 측면에서 교차하지 않는 경우는 생략되지만 유사한 인수로 증명할 수 있습니다.)

렉셀 정리의 증명: 두 개의 구면 삼각형 △ AC 1({displaystyle \displaystyle ABC_{1})과 △ AC 2({displaystyle \displaystyle ABC_{2}})가 점 A ∗ 및 B ∗를 통해 동일한 작은 원 l({displaystyle l})에 각각 정점을 가지고 있다면, 디스플레이스타일 B^{\}와 C1}의 새로운 세그먼트 C_1}를 생성한다C2D2(표시 스타일 C_{2}D_{2})는 AB에 일치하며, 정점 D1(표시 스타일 D_{1})과 D2(표시 스타일 D_{2})는 L.(표시 스타일 L.)에 있다. 2개의 사변형 ◻ A B1D1(표시 스타일 \square ABC_{1}) 및 ◻ B2(B2)는 평행한 구형이다,각각의 삼각형과 합동 사본을 붙여 만든 것입니다.보조 인자에 의해 두 평행사변형의 면적은 동일하므로 원래 삼각형의 면적도 같아야 합니다.

반대의 증거:만약 두 개의 구면 삼각형이 같은 면적을 가지고 있고 두 번째 삼각형의 정점이 첫 번째 삼각형의 렉셀 원에 있지 않다고 가정한다면, 두 번째 삼각형의 한 쪽을 통과하는 선은 렉셀 원과 교차하여 두 번째 삼각형과 다른 면적을 가지지만 첫 번째 삼각형과 같은 면적을 가진 새로운 삼각형을 형성할 수 있습니다.모순점이 주장은 요소 I.39에서 발견된 것과 동일합니다.

사케리 사각형

중앙점 원을 사용한 또 다른 증거는 카를 프리드리히 가우스(1841)가 삼각형의 측면과 m에 대한 수직 투영 사이에 형성된 사변형(인접한 두 직각과 다른 두 등각을 갖는 사변형)을 만들었다는 것이다,삼각형과$$^{[11] [12]}면적이 같습니다.

$A$$',$ {\$displaystyle$A${\displaystyle \text{'},}${\$displaystyle$ B$',$ {\$displaystyle$ C$'$ C'를 삼각형 꼭짓점의${\displaystyle }$m에 수직으로 투영합니다$.$$$ 결과적으로 생성된 직각 삼각형${\displaystyle \mathrm{}쌍}$ ${\displaystyle {△}^{}}$ ${\displaystyle {}^{}}$ $triangle$ M$$1 \$displaystyle$ AA$'$$M_{1}}$과${\displaystyle \mathrm{}}$$△{\displaystyle \mathrm{}}$ ${\displaystyle {}^{}}$$shaded$ M1$({$ CC$'M_{1}}($빨간색)은 $({$1$}})$에서 동일한 각도와 동일한 빗변을 가지므로 일치합니다. 삼각형 △ ${\displaystyle {}^{}triangle{}_{}}$ $($ BB$')$도 마찬가지입니다.$M_{2}}$ 및$$ $△{\displaystyle \mathrm{}}$ $'$ $(파란색)$입니다.따라서 삼각형의 면적 $△{\displaystyle }$ ${\displaystyle \mathrm{AB}}$ C$(표시$ 스타일 $\square$ ABC$)$는 사케리 사각형의 면적 ◻ ${\displaystyle {}^{}}$ B${\displaystyle {}^{}triangle{}^{}}$ A$',$ {\$표시$ 스타일 $\square$ ABB$'$와 같습니다.$각각$ 하나의 빨간색 삼각형$,$ 하나의 파란색 삼각형 및 녹색 사각형 $◻{\displaystyle }$ ${\displaystyle {}_{}}$ ${\displaystyle {M\mathrm{}}_{}}$ 2 ${\displaystyle {}_{}{}_{}}$ {{\$displaystyle \square$ ABM_${2}M_{1}}$이(가) 함께 붙여졌습니다. ($'{{\$ C$'$가 호 $A{\displaystyle {}^{}}$ '${\displaystyle B\text{'},}${\$displaystyle$ A$'B$$'$ 밖에 있으면 빨간색 또는 파란색 삼각형이 음의 영역에 부호를 갖게 됩니다.왜냐하면 $큰{\displaystyle }$ 원${\displaystyle }$m$,$ 즉 \$displaystyle$ m$$$,$ 즉 사각형 $◻{\displaystyle }$ ${\displaystyle {}^{}}$′ ${\displaystyle A\text{'},}$\$displaystyle \square$ ABB$'$ 때문입니다.A$',}$은(는) 렉셀 $원{\displaystyle }$l에 있는 C${displaystyle$ C$}$의 모든 선택에 대해 동일하며$,$ {{displaystyle l$,}$에$$해당하는 삼각형의$$ ${\displaystyle \mathrm{면적}}△{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{ABC}}${$displaystyle$ \$display$ ABC$}$는 $일정$합니다.

입체 투영법

입체 투영법은 구면을 평면에 매핑합니다.지정된 큰 원은 평면의 원시 원에 매핑되고 극은 각각 원점(원시 원의 중심)과 무한대의 점에 매핑됩니다.구면의 모든 원은 평면에서 원 또는 직선에 매핑되며, 직선은 두 번째 극을 통과하는 원을 나타냅니다.입체 투영은 각도를 보존한다는 의미로 등각도입니다.

일반적인 구면 삼각형에${\displaystyle \mathrm{}\mathrm{대한}\mathrm{관계}}$를 증명하려면$,$ 일반성 $정점{\displaystyle }$ A의$손실$이 없는 \$displaystyle \displaystyle$ $ABC$$,}$를 원점으로 투영하는 점으로 간주할 수 있습니다.그런 다음 구면 삼각형의 변은 두 개의 직선 세그먼트와 원형 호로 투영됩니다.만약 다른 두 꼭짓점의 원형 변에 대한 접선이 E 지점에서 교차한다면, 평면 직선 사면의 사각형 ◻ ABEC가 형성될 수 있으며, E 지점에서의 외각은 구형 초과 θ = θ A + θ B + θ C - θ C - θ \ displaystyle \vpsilon = A +\angle B+\anglegangle B+ C-C-각이다구면 삼각형의 \$pi$$}.$이것은 두 개의 1905년 ^[13]논문에서 대중화한 결정학자 주세페 세자로[de;fr]의 이름을 따서 때때로 구형 삼각법의 세자로 방법이라고 불립니다.

폴 세렛(1855년, 체사로보다 반세기 전)과 알렉산데르 시모니치(2019년)는 렉셀의 정리를 증명하기 위해 체사로의 방법을 사용했습니다.$({$$displaystyle$$$O$$})를$$ $BC가$투영하는 원형 호 평면의 중심으로 합니다$.$그렇다면 ◻ OBE C(\displaystyle \square OBEC)는 직각이므로 중심각 θ BOC(\displaystyle \angle BOC)는 삼각형의 구면 초과 θ({style E,})에서 외부각과 같다그의 내접각 정리는 ${\displaystyle \frac{12}{}\mu }$를 $측정$했습니다$.$ {\$displaystyle${$1}{2}\varepsilon.}$ 이$$ 관계는$C$의 $임의$의 선택에 대해 보존됩니다. 따라서$,$ 삼각형의 구면 초과는 $C$가 $렉셀{\displaystyle }$ 원 l$,$ {\$displaystyle$$$l$,$평면에서$$ B $∗$ {\$displaystyle$ B$^{*}$를 $통과$하는 선으로 투영됩니다.(삼각형의 면적이 반구보다 클 경우 유사한 주장을 할 수 있지만$,$ E{$displaystyle$ E$$$}$ $점$은 더 이상 ${\displaystyle \mathrm{각도}}{\displaystyle \mathrm{}}$∠${\displaystyle \mathrm{BOC}}$의$$내부가 아닙니다$.$ \$displaystyle \angle$ BOC입니다.$}$)^[14]

극삼각형의 둘레

만약 삼각형 △ A triangle B shaded C shaded C triangle (주황색 보라색)가 △ ABC의 극삼각형이라면, 정점 A ′, B c, C ′는 각각의 변 B, C, C, C, C의 극점이다,반대로, $꼭짓점{\displaystyle }$ $A$$$변 B${\displaystyle {}^{}}$′ ${\displaystyle {}^{}}$▁${\displaystyle c{}^{}}$ C$$ A$$${\displaystyle {\prime }^{}}$ ${\displaystyle {}^{}}$ ▁${\displaystyle a{}^{}}$ A ▁b A ′ B${\displaystyle }$▁. B$$$$▁the A$display$ A ▁{\ $B$ity A$a$ B } A $style$ B ' A b B a A ▁dual B ▁and B ' A c B ▁a B , A ▁versa B ▁polar B ▁exchanges A ▁the B ▁triangles A ▁the B ▁of A ▁( B ▁angles B ▁vice B ▁the B di A ) B ▁poles B style B , B ▁vertices B ▁sides A ▁b A ▁angles B display

쌍대삼각형의 각 변은 원래 삼각형의 내각을 보충하기 때문에, △ ABC의 구면 과잉은 쌍대삼각형의 주변 p'{\displaystyle p'}의 함수이다. △ A triangle B ε C triangle {\displaystyle \varepsilon } :

$표시(\style\varepsilon &=\angle A+\angle B+\angle C-\[3mu]&=(\pi-B'C')+(\pi-C')+(\pi-A'B')--\pi \[3mu]&=2\pi-pi').\end{aligned}}}$

1854년 조지프-에밀 바르비에(Joseph-Emile Barbier)와 페예스 토트 라슬로(László Fejes Toth)는 극이중성 하에서 외접하는 렉셀 원 l(\displaystyle l\displaystyle l}△ A displ B^{C})가 외접원이 되는 것을 주목하면서 극삼각형을 증명에 사용했다△${\displaystyle \mathrm{}{}^{}}$ $triangle$B ${\displaystyle {▁}^{}}$c C $′$ {\$displaystyle A'B'C}($$원형$ $삼각형$의 원)의 ystyle l$'}$이$($가) A$′$ ${\displaystyle B{}^{\text{'}}}$에$$외부적으로 접합니다.$}$^[15]

만약 꼭짓점 C가 l,{displaystyle c}를 따라 이동한다면, A'B' 변은 변하지만 항상 같은 원 l'. .{displaystyle l'.} 원의 각 꼭짓점에서 인접한 접점까지의 거리가 같기 때문에 A = A t T C는 A 'style A'를 표시한다$T_{B}=A'$$T_{C}}($파란색 세그먼트) $및{\displaystyle {}^{}}$ B${\displaystyle {\text{'}}^{}}$ ${\displaystyle T{}_{}}$ ${\displaystyle A_{}}$= ${\displaystyle {}^{\text{'}}}$ $({$ B$)$$T_{A}=B'$$T_{C}}($빨간색 세그먼트), $둘레{\displaystyle {}^{}}$ p$'{{$ p$'}$는

$디스플레이({style begin{aligned}p'&=A)B'+B'C'+C'A'\\[3mu]&=(A'T_{C}+B'T_{C}}+C'B'+C'A'\\\[3mu]&=(C'A'+A')T_{B}}+(C'B'+B')T_{A}\\[3mu]&=C'T_{B}+C'T_{A},\end{aligned}}}$

$원{\displaystyle {}^{}}$ l$'{$$displaystyle$ l$}$에만 의존하지만 변화하는 $'B'$에는 의존하지 않습니다.} 반대로 점 C가 l에서 벗어나면 연관된 원 '{displaystyle l'은 크기가 변하며, 점 TA({displaystyle T_{A})와 TB({Displaystyle T_{B})는 C' δ({displaystyle C'^{*})를 향해 또는 양쪽으로 이동하고 경계 P'(\displaystyle P')△ C'의 경계를 변경한다 $displaystyle$\"$B'C'\!"$을(를) 표시하여$ε을($를) 변경합니다. ${\varepsilon}$을(를) 변경합니다${\displaystyle .{}^{}}$

$따라서{\displaystyle }$$θ$가 상수인 점 $({displaystyle$$C})$의 궤적은 l$({displaystyle$ $l$$.})$입니다.

삼각 증명

렉셀 c.(1777)과 오일러 (1778) 모두 그들의 논문에 삼각법 증명을 포함했고, 나중에 몇몇 수학자들은 삼각법 증명을 제시했는데, 여기에는 아드리앙-마리 레전드레 (1800), 루이 푸아상 (1842), 이그네스-루이-알프레드 르 코인 (1858), 그리고 조셉-알프레드 세렛 (1862)이 포함됩니다.이러한 증명은 코사인의 구면 법칙 또는 구면 초과에 대한 공식과 같은 알려진 삼각 관계에서 시작하여 삼각형 ^[16]동일성의 대수적 조작으로 진행됩니다.

렉셀 원의 반대쪽 호

구면은 큰 $원{\displaystyle }$ $,$ {\$displaystyle$ AB$}$에 의해 두 개의 반구로 분리되며, A ${\displaystyle {\ast }^{}}$ {\$displaystyle$ A$^{*}$ 및 B $∗$ {{\$displaystyle$ B$^{*}}$를 $통해{\displaystyle {}^{}}$ 모든 렉셀 원은 각 반구에 하나씩 두 개의 호로 분리됩니다.$점{\displaystyle }$X({$displaystyle$X})가$$$$ C$({displaystyle$ C$})$와 반대 호에 있는 경우${\displaystyle \mathrm{}}$$△{\displaystyle \mathrm{}}$$({displaystyle$ \$displaystyle$ABC$$})와 $△$ $({displaystyle$ \$displaystyle$ABX$$})의 영역은 일반적으로 다릅니다.그러나 구면 표면적이 경계 방향에 의해 결정된 부호로 부호화된 것으로 해석되면 삼각형${\displaystyle \mathrm{}}$$△{\displaystyle \mathrm{}}$ $디스플레이$스타일 \$displaystyle ABC$와 △ ${\displaystyle \mathrm{ABX}}$ $\displaystyle ABX는$$$반대 부호를 가지며 반구의 면적에 따라 다릅니다.

렉셀은 좀 더 일반적인 틀을 제안했습니다.두 개의 뚜렷한 반원형이 아닌 $점{\displaystyle }$ A$({displaystyle$ A$}$ $및$ B$({displaystyle$ B$)$가 주어지면 두 개의 대원형이 결합됩니다. 하나는 반원형보다 짧고 다른 하나는 더 긴 것입니다.점의 $삼중{\displaystyle }$ A$,$ $, C$가 주어지면, 일반적으로$△{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{ABC}}$ $디스플레이$$스타일$ \$timeout$ ABC$}$은 각 쌍을 연결하는 세 개의 짧은 호로 둘러싸인 영역을 의미하는 것으로 해석됩니다.그러나 각 쌍에 대해 호를 선택할 수 있도록 허용하면 8개의 구별되는 일반화된 구형 삼각형을 만들 수 있으며, 일부는 자체 교차점을 가지며, 이 중 4개는 기본$AB$가 동일한 $것$으로 간주될 수 있습니다$.$

이 여덟 개의 삼각형이 모두 동일한 표면적을 가지고 있는 것은 아니지만, 경계 방향에 의해 결정된 기호로 영역이 서명된 것으로 해석된다면, ^[17]반구의 면적에 따라 다른 것들이 다릅니다.

이와 관련하여, 구 위의 4개의 뚜렷한 비구형 점 A, B, C, C, C, X가 주어졌을 때, 렉셀의 정리는 일반화된 삼각형 △ ABC의 부호 있는 표면적이 일반화된 삼각형 △ B X의 부호 있는 표면적과 다르다는 것을 주장한다$e$A${\displaystyle {}^{}}$${\displaystyle {\ast ,}^{}}$ {\$displaystyle$ A$^{*}\!,}$ $B$$∗,$ {\$displaystyle$ B$^{*}\!,}$ $C$$,$ {\$displaystyle$ C$,}$ $및$ X {\$displaystyle$ X$}$가 순환하는 $경우$에만 전체 반구 수에 의한 \$triangle ABX}.$

특수한 경우

달의 퇴화

정점 C({displaystyle C})가 기저 꼭짓점에 대척점(예: B ∗ {\displaystyle B^{*})에 접근하면, 한계에서 삼각형은 B ∗에서 l({displaystyle l})에 접하는 선과 대척점 작은 원 l({\displaystyle l})에 접하는 선으로 퇴화된다 B, \displaystyle B,}에서, 그리고 l. \displaystyle l.의 같은 호에 정점을 갖는 삼각형들과 같은 초과 δ \varepsilon을 갖는다. 축퇴 삼각형으로서, A \displaystyle A}(즉, δ A = \pi, 반회전)에서 직선각을 가지며, B = B δ δ = 2 δ이다.표시({style B=B^{*})$=tftfrac {1}{2}}\varepsilon.}$

C{displaystyle C}가 반대 방향(렉셀 원의 다른 호를 따라)에서 B∗{\displaystyle B^{*}에 접근할 때, 한계에서 삼각형은 반대 방향과 각도 θ B = θ B = - 1 θ - 2 θ \displaystyle B = \ang에서 렉셀 원에 접하는 동일한 구면으로 퇴화된다$le B^{\star}=\pi -{\tfrac{1}{2}}\varepsilon.}$

반구형 영역

구면 삼각형의 면적은 렉셀 원 A ∗ B ∗ B ^{*}B^{*}C가 대원 B, 즉 A ∗ B ∗ B ∗ B ∗ B excess B π B ε B of B a B style B a B ^ B * B { B style B { B ab B the B { B circle B ogonal B is B c B ∗ B to B arc B that B ∗ B and B the B π B a B ∗ B is C the C great B a B ell${*}C$$}$ 및 호 $({displaystyle$ AB$})$는 ABC${\displaystyle {}^{}}$∗의 직경입니다$.$ {{$displaystyle$ ABC$^{*}\!$$}$

이 경우, D({displaystyle D})를 렉셀 원 A ∗ B ∗ C({\displaystyle A^{*}B^{*}C)에서 C({displaystyle C})와 정반대의 점으로 하고, 4개의 삼각형 △ ABC({\displaystyle A^{*}, {\displaystyle ABC}), △ B(\displaystyle C), 그리고 DC(Displaystyle C)와 정반대의 점이 된다일치하며, 함께 구형 디스패노이드 $(displaystyle ABCD$)$$를 형성합니다.${\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$ ${\displaystyle {}^{}}$ $∗$ {{\$displaystyle$ AA$^{*}BB^{*}CC^{*}DD^{*}$는 직사각형 정육면체의 ^[19]정점입니다.

관련 개념 및 결과

구면 평행사변형

구면 평행사변형(球面∠形, )은 정반대의 변과 정반대의 각이 일치하는 구면의 사각형 ◻ ABCD(\displaystyle \square ABCD,\displaystyle AB\cong CD,} BC ∠ DA, {\displaystyle BC\cong DA,} ∠ A = ∠ C, \displaystyle D\displaystyle D\displaystyledisplaystyle\displaystyle\d.여러 면에서 평면 평행사변형과 유사합니다.두 대각선 AC와 BD는 서로 양분하고 도형은 교차점에 대한 2배 회전 대칭을 갖는다. (따라서 대각선은 평행사변형을 두 개의 합동 구면 삼각형, △ ABC triangle △ CD A \ displaystyle ABC \ con \ display CDA 및 △ B D △ C c DST)$yle \triangle$ ABD$\cong \triangle CDB$);$$ 만약 어느 한 쌍의 반대쪽의 $중간점$이 큰$$원 m${displaystyle$ m$\}$에 의해 연결된다면, 네 개의 꼭짓점은 그것으로부터 등거리에 있는 두 개의 평행한 작은 원 위에 놓입니다.좀 더 구체적으로, 구형 평행사변형의 모든 $(예$: D{$displaystyle$ D})은 인접한 꼭짓점 중 하나를 통과하는 두 개의 렉셀 원($}$과 ${$의 교차점에 있고 다른 두 꼭짓점과 반대되는 점에 있습니다.

구면 삼각형과 마찬가지로, 동일한 Lexell 원에 있는 꼭짓점과 밑면이 같은 구면 평행사변형은 동일한 면적을 갖습니다. 위의 § 구면 평행사변형을 참조하십시오.구면 삼각형에서 시작하여, 두 번째 합동 삼각형은 임의의 변의 중간점을 가로지르는 (구면) 점 반사를 통해 형성될 수 있습니다.이 두 삼각형을 조합하면 원래 ^[20]삼각형의 면적이 두 배인 구형 평행사변형이 됩니다.

솔린의 정리 (극쌍성)

렉셀 정리의 극쌍대칭은 1825년에 삼각법으로 증명한 A. N. J. 솔린의 이름을 따서 소린의 정리라고 불리기도 하는데, 이는 고정된 큰 원에 변들이 있는 구형의 3각형 △ bc \displaystyle a, b\displaystyle a, b\displaystyle abc)와 고정된 둘레 p = a ⌢ + ⌢ + b + thus + triangle이다 c ⌢, \"displaystyle p=displaystyle abc\"의 외피는 a, b, displaystyle a, b에 내부적으로 접하며, c, displaystyle c에 외부적으로 접하는 작은 원이다. △ b, displaystyle abc.조지프 에밀 바르비에는 나중에 기하학적 증명(1864)을 작성하여 렉셀의 정리를 이중성으로 증명했습니다.^[21]

이 결과는 유클리드 기하학과 쌍곡선 기하학에도 적용됩니다. 바비에의 기하학적 주장은 유클리드 또는 쌍곡선 평면에 직접 이식될 수 있습니다.

구면의 엽면

$임의$의 $기저{\displaystyle }$에 대한 Lexell의 위치는 구면(1차원 잎으로 분해)을 형성합니다$.$이 로키는 A ${\displaystyle {\ast }^{}}$ {\$displaystyle$ A$^{*}$ 및 B$$ {{\$displaystyle$$$B$^{*}\!}$에 끝점이 있는 작은 원의 호이며, 여기서 중간점$$ $C$는$$고정 부호 영역의 삼각형 $ABC의$정점입니다$$.이 면적은 Lexell 원과 큰 $원{\displaystyle }$ A ${\displaystyle {}^{}}$$$${\displaystyle {\ast }^{}}$ {\$displaystyle$ A$^{*}$ $또는$ B $∗$ {\$displaystyle$ B$^\{*\}$ 지점 중$$ 하나에서 Lexell 원과 B ∗ ${\displaystyle {}^{}{}^{}}$ § B $^{*}$ 사이의 부호 있는 각도의 두 배입니다. 위의 ∗ 음력 퇴화를 참조하십시오.그림에서 Lexell 원은 녹색입니다. 단, 삼각형의 면적이 검은색 반구의 배수이고 면적이 표시된 반구형의 경우는 제외합니다. 위의 ^[22]§ 반구형 영역을 참조하십시오.

구속조건에 따른 구형 삼각형 면적 최대화

1784년 니콜라 푸스는 주어진 원 위에 정점 C가 있는 주어진 기저 AB의 최대 면적의 삼각형을 찾는 문제를 제기했고 해결책은 C의 극소변형인 C를 포함하는 주장을 사용했다또한 렉셀 정리의 직접적인 결과: 정점을 통과하는 렉셀 원 $A{\displaystyle {}^{}{\ast }^{}}$ ${\displaystyle {}^{}{}^{}}$ $∗$ ${\displaystyle {}^{}}$ {\$displaystyle$$$A$^{*}B^{*}$C는$C$에서 g$${\$displaystyle$ g$}$에 접해야 합니다$.$$}$

만약 ${displaystyle$ g$}$가 점 P${displaystyle$ P$\}$에서 ${displaystyle$ AB$}$를 통과하면, 탄젠트-세컨트 정리의 구면 유사체에 의해 원하는 탄젠트 지점까지의 $각거리{\displaystyle }$ ${displaystyle$ PC$}$는 다음을 만족합니다.

${\displaystyle \tan^{2}{\tfrac {1}{2}} 표시PC=\tan{tfrac{1}{2}}PA^{*}\,\tan{tfrac{1}{2}}PB^{*},}$

여기서 우리는$$$△{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{ABC}}$ {\$displaystyle \displaystyle$ ABC$}$가 최대 ^[23]면적을 갖도록 점$C{\displaystyle }$ {\$displaystyle$ C$}$를 n \$displaystyle$ g$}$에 명시적으로 구성할 수 있습니다.

1786년에 테오도르 폰 슈베르트는 주어진 기저와 고도의 최대와 최소 면적의 구면 삼각형(기저를 포함하는 대원점에서 수직으로 떨어지는 구면 길이)을 찾는 문제를 제기했고 해결했다.ude circle")는 베이스를 포함하는 큰 원과 평행합니다.슈베르트는 최소 면적의 삼각형이 고도 원과 기저의 수직 이등분선의 가장 가까운 교차점에 정점을 두고 최대 면적의 삼각형이 가장 먼 교차점에 정점을 두고 있다는 것을 보여주기 위해 미적분 기반 삼각형 접근법으로 이 문제를 해결했습니다.하지만, 이 정리는 또한 렉셀 정리의 직접적인 결과입니다: 렉셀 원은 가장 작고 가장 큰 삼각형 영역을 나타내는 기저 꼭짓점과 반대되는 점을 통해 고도 원에 접하는 점입니다.2019년 빈센트 알베르게와 엘레나 프렌켈은 쌍곡선 ^[24]평면에서 유사한 문제를 해결했습니다.

면적 이등분선에 대한 슈타이너 정리

유클리드 평면에서 삼각형의 중위수는 꼭짓점과 반대쪽의 중간점을 연결하는 선분입니다.삼각형의 세 중위수는 모두 그 중심에서 교차합니다.각 중위수는 삼각형의 면적을 이등분합니다.

구면에서 삼각형의 중위수는 꼭짓점과 반대쪽의 중간점을 연결하는 대원호로 정의될 수도 있습니다.세 개의 중위수는 모두 한 점에서 교차하며, 삼각형의 외심 중심에 대한 중심 투영, 즉 구가 3차원 유클리드 공간에 포함된 경우 세 개의 점을 포함하는 평면 삼각형의 중심입니다.그러나 구체에서 삼각형의 면적을 이등분하는 하나의 꼭짓점과 반대쪽의 점을 통과하는 대원호는 일반적으로 해당 중위수와 구별됩니다.

Jakob Steiner는 Lexell의 정리를 사용하여 이 세 개의 면적 이등분 호 (그가 "등각자"라고 부르는)가 모두 한 점에서 교차한다는 것을 증명했습니다. (중심의 다른 구면 유사체는 원래의 변의 기저가 되는 동일한 면적의 세 개의 삼각형의 정점입니다.)삼각형, (${\displaystyle \frac{13}{},}$ ${\displaystyle \frac{13}{},}$ $){$^[25]tfrac{1}{3}},{\tfrac{1}{3}},{\tfrac{1}{3}}}}을 구면적 좌표로 갖는${\displaystyle }$점.)

구면 영역 좌표

아핀 공간에서 주어진 삼각형에 상대적인 점에 대한 무게중심 좌표계는 구면 기하학에서 완벽한 유사성을 가지지 않습니다. 모든 특성을 공유하는 단일 구면 좌표계는 없습니다.하나의 부분적 유사성은 주어진 구면 삼각형 $△{\displaystyle \mathrm{}}$ $,$ \$displaystyle \displaystyle$ $ABC$$,}$에 상대적인 점$P$에 대한 구면 영역 좌표입니다.

$디스플레이 스타일 \left({\frac \\varepsilon _{PBC}}{\varepsilon _{ABC}},{\frac \varepsilon _{ABC}},{\frac \varepsilon _{ABC}},{\frac \varepsilon _{ABC}}),$

여기서 각 양 ${\displaystyle {\epsilon }_{}}$ ${\displaystyle {\mathrm{QRS}}_{}}$는$\$를 $표시$합니다.$RS}$은 해당 구형 삼각형$$△ ${\displaystyle \mathrm{QRS}}$ . {\$displaystyle$\displaystyle QRS$}$의 부호 $있는$ 구형 초과입니다. 이 좌표는 1$,{displaystyle$ 1$,}$에 달하며 평면에서 동일한 정의를 사용하면 무게 중심 좌표가 생성됩니다.

렉셀의 정리에 따르면, 하나의 좌표 상수를 갖는 점들의 궤적은 해당 렉셀 원입니다.따라서 두 개의 작은 원을 교차하여 주어진 세 개의 구형 영역 좌표에 해당하는 점을 찾는 것이 가능합니다.

각 구면 영역 좌표를 사용하여 평면의 해당 무게중심 좌표를 사용하여 구면 삼각형을 다른 삼각형 또는 평면 삼각형에 매핑할 수 있습니다.이것은 다면체 지도 투영법, 이산 전역 그리드의 정의 또는 구 또는 ^[26]구와 위상적으로 동일한 삼각망을 매핑하는 구 또는 텍스처의 매개변수화에 사용될 수 있습니다.

유클리드 평면

유클리드 평면에서의 렉셀 정리의 유사성은 고대에서 왔으며, 명제 35에 기초한 명제 37과 39의 유클리드 원소 1권에서 찾을 수 있습니다.평면에서, Lexell의 원은 ^[4]기저부에 평행한 직선(Lexell의 선이라고 할 수 있음)으로 퇴화합니다.

요소 I.35는 상단 면이 선형인 동일한 기저를 가진 평행사변형이 동일한 면적을 갖는다는 것을 유지합니다.증명:두 평행사변형을 ◻ ABC 1 D1(디스플레이 스타일 \square ABC_{1}D_{1}) 및 ◻ ABC 2 D2({2}), 공통 기저 AB와 C1(디스플레이 스타일 C_{1}), C1(디스플레이 스타일 C_1), C2(D1), C2(D2), C2(D2)로 하고 C2(D2)를 C2(D2), C2(D2), CstylearallearallearallearallearallearallearallearallearallearallearalBC 1({displaystyle BC_{1}})과 AD 2({displaystyle AD_{2}) 사이의 교차점입니다. 그러면 두 상단 면은 합동 C1 D1 ≅ C2 D2 D2 \cong C_{1}\cog C_{2}이므로 각 C2 D2 {1}에 중간 세그먼트를 추가합니다.따라서$$ 두 삼각형 $△{\displaystyle \mathrm{}}$ ${\displaystyle {BC\mathrm{}}_{}}$ 1 ${\displaystyle {C\mathrm{}}_{}}$2{{$displaystyle$ \displaystyle$$$BC_{1}C_$${$${\displaystyle 2}$$}}$ ${\displaystyle {및\mathrm{}}_{}}$ △ ${\displaystyle {AD\mathrm{}}_{}}$1 D 2{$displaystyle$ \displaystyle $AD_{1}D_{2}}$의 변은 일치하므로 일치합니다.이제 각 평행사변형은 삼각형에 ${\displaystyle {}_{}}$된$$ 중 하나로 형성됩니다. 삼각형 $△{\displaystyle \mathrm{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {}_{}}$ F${displaystyle D_{2}C_{1}F$를 잘라낸 다음,따라서 두 평행사변형 $◻{\displaystyle }$ ${\displaystyle {AC\mathrm{}}_{}}$ 1 $({$ ABC_${1}D_{1})$과 ◻ ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ $({$ ABC_${2}D_{2}})$는 동일한 면적을 갖습니다.

요소 I.37은 기저와 평행한 동일한 선의 정점과 기저를 가진 삼각형이 동일한 면적을 갖는다고 가정합니다.증명:삼각형${\displaystyle \mathrm{}}$$△{\displaystyle \mathrm{}}$ ${\displaystyle {}_{}}$ $({$ ABC_${1$$})$ 및 △ ${\displaystyle {AC\mathrm{}}_{}}$ 2$({$$displaystyle$\$displaystyle ABC_$${$$2})$가 각각 $AB$와 평행한 $동일$한$$선에 정점을 두도록 합니다$.$} 정점 D1({displaystyle D_{1})과 D2({style D_{2})를 L.displaystyle L.D.}에 일치시키는 새로운 세그먼트 C1 D1({1})과 C2({displaystyle C_{2})를 구성합니다. 4중 모눈 ◻ B1({displaystyle D_{2})와 ABC({style D1})$_{2}D_{2}}$은(는) 각각의 삼각형과 합동 사본을 붙여 만든 평행사변형입니다.I.35에서는 두 평행사변형이 동일한 면적을 가지므로 원래 삼각형도 동일한 면적을 가져야 합니다.

요소 I.39는 반대로, 동일한 기저의 동일한 측면에 있는 동일한 면적의 두 삼각형은 기저와 평행한 선에 정점을 갖습니다.증명:만약 두 개의 삼각형이 같은 밑면과 같은 면적을 가지고 있고 두 번째 삼각형의 정점이 첫 번째 삼각형을 통과하는 밑면과 평행한 선("렉셀 선")에 있지 않다고 가정한다면, 두 번째 삼각형의 한 쪽을 통과하는 선은 두 번째 삼각형과 다른 면적을 가지는 새로운 삼각형을 형성하기 위해 렉셀 선과 교차될 수 있습니다.첫 번째 삼각형과 같은 면적, 모순.

유클리드 평면에서 삼각형$△{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{AB}}$C의 면적$$$ε$${{$$displaystyle$ \$varepsilon$$}$은 임의의 변 길이(밑면)와 베이스를 통과하는 선과 정점을 통과하는 평행선 사이의 거리(해당 높이)를 사용하여 계산할 수 있습니다.$점{\displaystyle }$ C$({displaystyle$ C$})$를 정점으로 사용하고, 구형의 경우에 대한 유사성을 보다 명확하게 하기 위해 전통적인 동일성의 ${\displaystyle \frac{\mathrm{양쪽}}{}}$에$12({tdisplaystyle$ {1$$$}{2}}$를 곱하면 다음과 같습니다.

$표시({style\tfrac {1}{2}}\varepsilon =tftfrac {1}{2}}c\,{\tfrac {1}{2}}h_{c})}$

유클리드 정리는 구에 대한 렉셀 정리의 결과로 볼 수 있습니다.구면의 곡률이 0에 가까워질수록 제한적인 경우입니다. 즉, 구면의 반지름에 비례하여 무한대로 작은 구형 삼각형의 경우입니다.

쌍곡면

쌍곡선 평면에서 삼각형 △ AC가 주어지면, 삼각형 △ ABX와 같은 변수 점 X의 궤적은 △ ABC와 같은 면적을 가진다$eB,}$ 렉셀의 하이퍼사이클이라고 할 수 있습니다.구에서 나온 여러 증명들은 쌍곡선 평면에서 직접적인 유사점을 가지고 있는데, 바르빈(1902)의 사케리 사변형을 통한 가우스식 증명과 파파도풀로스 & 수(2017)의 쌍곡선 평행사변형을 통한 오일러식 증명을 포함한다,그리고 Shvartsman(2007)의 입체 투영을 통한 Paul Serret 스타일의 증명.[27]

구면 기하학에서 대척점 변환은 각 점을 대척점(직경적으로 반대)으로 가져갑니다.유클리드 공간에 포함된 구의 경우, 이것은 구의 중심을 통한 점 반사이고, 평면에 입체적으로 투영된 구의 경우, 원점을 가로지르는 점 반사로 구성된 원시 원을 가로지르는 반전입니다.원시 원의 반지름과 동일한 크기의 가상 반지름 원의 반전).

평면 쌍곡선 기하학에서, 유사한 대척점 변환이 있지만, 임의의 두 대척점은 이중 쌍곡선 평면의 서로 반대되는 가지에 있습니다.민코프스키의 기호 공간(-, + , + ), {\displaystyle (-, +), (-, +), (-, +)에 내장된 두 장의 쌍곡선 모형에 대해, 대척점 변환은 쌍곡선 모형의 중심을 통과하는 점 반사이다각 점을 반대쪽 반평면으로 가져가는 이상적인 점의 원선; 등각 디스크 모델에서 그것은 경계 원을 가로지르는 반전으로, 디스크의 각 점을 보완의 점으로 가져갑니다.구와 마찬가지로, 쌍곡선 기하학에서 한 쌍의 대척점을 통과하는 일반화된 원은 ^[28]측지선입니다.

평면 및 구면 삼각형 영역 공식과 유사하게,삼각형의 쌍곡선 영역 ε{\displaystyle \varepsilon}은 기본 c{displaystyle c}(호 A B의 쌍곡선 길이)와 "높이" h c{{c}(평행 하이퍼사이클 A ∗ B ∗ B ^{*} C와 B C 사이의 쌍곡선 거리)로 계산할 수 있다$$):

$디스플레이 스타일 \sin{tfrac{1}{2}}\varepsilon =\tanh{1}{2}c\,\tanh{tfrac{1}{2}h_{c}}$

구형의 경우와 마찬가지로, 작은 삼각형 한계에서 이것은 평면 공식으로 감소합니다.

메모들

레퍼런스