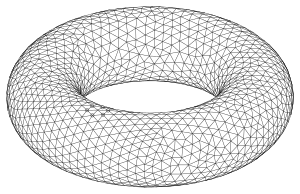
표면 삼각측량

트라이앵글 메쉬를 이 기사로 통합하자는 의견이 제기되었다. (토론) 2021년 5월부터 제안.

지표면 평균의 삼각 측량

• 주어진 표면을 부분적으로 또는 전체적으로 덮는 삼각형의 그물 또는
• 그러한 삼각망 그물의 점과 삼각망을 생성하는 절차

접근

이 글은 삼각망 그물의 생성을 기술하고 있다. 문헌에는 주어진 순의 최적화를 다루는 기여가 있다.

표면 삼각측량은 다음에 대해 중요하다.

• 표면 시각화 및
• 유한 요소 방법의 적용

파라메트릭으로 정의된 표면의 삼각측정은 정의 영역을 삼각측량함으로써 간단히 달성된다(Monkey Saddle을 묘사하는 두 번째 그림 참조). 그러나 삼각형은 모양과 물체 공간의 확장에 따라 다를 수 있어 잠재적인 결점이 있다. 매개변수 영역을 삼각측량하면서 단계 폭을 고려하는 적응적 방법을 통해 이를 최소화할 수 있다.

암묵적 표면(하나 이상의 방정식으로 정의됨)을 삼각측량하는 것은 더 어렵다. 본질적으로 두 가지 방법이 존재한다.

• 한 가지 방법은 3D 고려 영역을 정사각형으로 나누고 표면에 폴리곤을 얻기 위해 정육면체의 가장자리와 표면의 교차점을 결정하는데, 그 이후에는 삼각측량(커팅 큐브 방식)을 해야 한다.^[1][2] 데이터 관리를 위한 지출이 크다.
• 두 번째이자 간단한 개념은 행진법이다.^[3][4][5] 삼각형은 시작점에서 삼각형의 육각형으로 시작한다. 그리고 나서 이 육각형은 주어진 규칙에 따라 고려의 표면이 삼각형을 이룰 때까지 새로운 삼각형으로 둘러 싸여진다. 표면이 여러 구성 요소로 구성된 경우 적절한 시작점을 사용하여 알고리즘을 여러 번 시작해야 한다.

커팅 큐브 알고리즘은 동시에 규정된 한계 매개변수에 따라 주변 시작 큐브 내 표면의 모든 구성요소를 결정한다. 행군 방식의 장점은 경계를 정할 수 있다는 것이다(그림 참조).

폴리곤 메쉬 생성을 위한 표면 폴리곤화 평균.

표면의 삼각측량은 이산 지정 평면 점 집합의 삼각측정과 혼동해서는 안 된다. Delaunay 삼각 측량을 참조하십시오.

• 

  삼각측량: 실린더, ${\displaystyle {표면\mathrm{}}^{}}$ x $4{\displaystyle {}^{}}$+ ${\displaystyle {y\mathrm{}}^{}}$ 4${\displaystyle {}^{}}$+ ${\displaystyle {z\mathrm{}}^{}}$ ${\displaystyle {}^{}}$= ${\displaystyle 1}$ ${\displaystyle x^{4}+y^{4}+z^{4}=1$}

• 

  삼각측량: 실린더, ${\displaystyle {}^{}}$ $x{\displaystyle {}^{}}$ ${\displaystyle {4\mathrm{}}^{}}$+ z ${\displaystyle {4\mathrm{}}^{}}$= ${\displaystyle 1}$ ${\displaystyle x^{4}+y^{$4}+y^{$4}+z^{4}=1$ POV-Ray 영상

• 

  토러스: 행군 방법에 의해 삼각측량

• 

  Torus: 절단 큐브 방법에 의한 폴리곤화

참고 항목

• 컴퓨터 지원 설계
• 메쉬 생성
• 다듬기(컴퓨터 그래픽)
• 행진 큐브
• 점 집합 삼각 측량

참조

외부 링크

• Tasso Karkanis & A. James Stewart: 암묵적 표면의 곡률 종속 삼각측량 [1]

소프트웨어

• 점 구름 라이브러리의 지표면 재구성 자습서 및 지표면 삼각망 알고리즘 목록