누셀트 수

유체역학에서 누셀트 수(Nu)는 유체 내 경계에서의 대류 대 전도성 열전달의 비율이다.대류는 이류(유체 운동)와 확산(전류)을 모두 포함한다.전도성 성분은 대류와 동일한 조건에서 측정되지만, 가정적으로 움직임이 없는 유체에 대해 측정됩니다.이것은 무차원 수치이며 유체의 ^[1]^{: 466}레일리 수치와 밀접하게 관련되어 있습니다.

Nusselt 값 1(0)은 순수 ^[1]^{: 336}전도에 의한 열 전달을 나타냅니다.1(0)~10의 값은 슬러그 플로우 또는 층류 ^[2]특성입니다.Nusselt 수치가 클수록 일반적으로 100-1000 범위의 ^[2]난류를 가진 보다 활발한 대류에 해당합니다.누셀트 수는 대류 열전달 ^[1]^{: 336}과학에 큰 기여를 한 빌헬름 누셀트의 이름을 딴 것이다.

유사한 비차원 특성은 Biot 번호이며, 이는 유체가 아닌 고체 물체에 대한 열 전도율과 관련이 있습니다.누셀트 수의 질량 전달 유사체는 셔우드 수이다.

정의.

Nusselt 숫자는 경계를 통과하는 전도성 열전달에 대한 대류 비율이다.대류 및 전도 열 흐름은 서로 평행하고 경계 표면의 표면과 수직이며, 단순한 경우에는 모두 평균 유체 흐름과 수직입니다.

\mathrm {Nu} _{L}=blac {mbox {Converative 열전달}} =blac {h} {k/L} =blac {hL} {k}}

여기서 h는 흐름의 대류 열전달 계수, L은 특성 길이, k는 유체의 열전도율입니다.

특성길이의 선택은 경계층의 성장방향(또는 두께)이어야 한다. 특성길이의 예로는 (원통축에 수직인) 교차흐름의 실린더 외경, 자연대류를 하는 수직판의 길이 또는 구체의 지름 등이 있다.복잡한 형상의 경우 길이는 유체체의 부피를 표면적으로 나눈 것으로 정의할 수 있다.
유체의 열 전도율은 일반적으로(항상 그렇지는 않지만) 필름 온도에서 평가되며, 엔지니어링 목적으로는 벌크 유체 온도 및 벽 표면 온도의 평균으로 계산될 수 있습니다.

평균 Nusselt 번호로 알려진 위의 정의와는 대조적으로 국소 Nusselt 번호는 표면^[1]^{[page needed]} 경계에서 국소 관심 지점까지의 거리가 되는 길이를 취함으로써 정의된다.

\mathrm {Nu} _{x} = flac {h_{x} {k}

평균 또는 평균 숫자는 다음과 같은 ^[3]관심 범위에 걸쳐 식을 통합하여 구합니다.

{\mathrm {Nu}}=black {\frac {1}{L}}\int _{0}^{L}h_{x}\dx\L}{k}=black{\overline {h}}L}{k}}

맥락

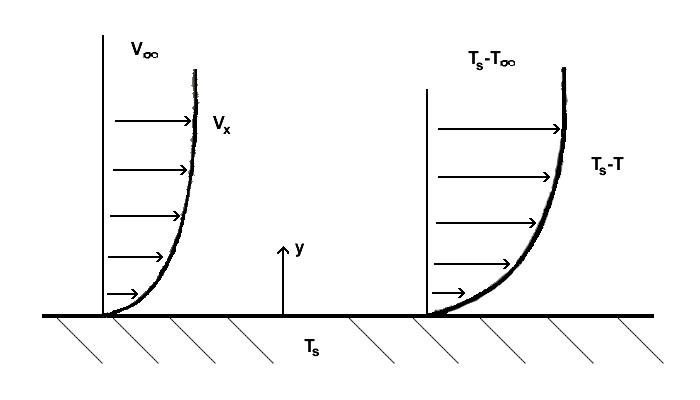
표면과 표면을 통과하는 유체 사이의 대류 열 전달을 이해하려면 대류 경계층에 대한 이해가 필요합니다.열경계층은 유체의 자유유동온도와 표면온도가 다를 경우 발생한다.온도 프로파일은 이 온도차에 기인하는 에너지 교환에 의해 존재합니다.

열경계층

열 전달 속도는 다음과 같이 뉴턴의 냉각 법칙을 사용하여 기록될 수 있습니다.

Q_{y}=hA\left(T_{s}-T_{\infty }\right)

y

Q_{y}=hA\left(T_{s}-T_{\infty }\right)

Q_{y}=hA\left(T_{s}-T_{\infty }\right)

A (

Q_{y}=hA\left(T_{s}-T_{\infty }\right)

-

Q_{y}=hA\left(T_{s}-T_{\infty }\right)

Q_{y}=hA\left(T_{s}-T_{\infty }\right)

)

Q_{y}=hA\left(T_{s}-T_{\infty }\right)

{

displaystyle

Q _ { y } =

hA \

left (

T

_ {

s

} - T _ { \

infty

} \

right )

,

여기서 h는 열전달계수이고 A는 열전달 표면적입니다.표면에서의 열 전달은 전도에 의해 이루어지기 때문에 열전도율 k:

=

\left(T-T_{s}\right)\right

_

{y=0

이 두 항은 같습니다.따라서

。{

\left(T-T_{s}\right)\right

_

{y=0

}=

hA\left(T_{s}-T_{\infty}\right

재배치,

。{

{\frac \left

(

T

_ { s

}

- T \ right } { \

partial

y } } \

right _

{ y =

0

} { \

left

( T _ {

s

} - T _ { \

inft }

} }

{\frac {h}{k}}={\frac {\left.{\frac {\partial \left(T_{s}-T\right)}{\partial y}}\right|_{y=0}}{\left(T_{s}-T_{\infty }\right)}}

} 。

대표 길이 L을 곱하면 차원이 없는 식입니다.

{\frac {hL}{k}}={\frac {\left.{\frac {\partial \left(T_{s}-T\right)}{\partial y}}\right|_{y=0}}{\frac {\left(T_{s}-T_{\infty }\right)}{L}}}

{\frac \left ( T _ { s } - T \ right } { \ partial y } \ right _ { y = 0 } { \ frac \ left ( T _ { s } - T _ { \ infty } }

L

이제 오른쪽은 기준 온도 구배에 대한 표면의 온도 구배 비율이고 왼쪽은 비오트 계수(Biot modulus)와 유사합니다.이는 누셀트 수 Nu라고도 하는 유체의 대류 열 저항 대비 전도성 열 저항의 비율이 됩니다.

\mathrm {Nu} ={\frac {h}{k/L}}={\frac {hL}{k}}

\mathrm {Nu} ={\frac {h}{k/L}}={\frac {hL}{k}}

\mathrm {Nu} ={\frac {h}{k/L}}={\frac {hL}{k}}

\mathrm {Nu} ={\frac {h}{k/L}}={\frac {hL}{k}}

k /

\mathrm {Nu} ={\frac {h}{k/L}}={\frac {hL}{k}}

\mathrm {Nu} ={\frac {h}{k/L}}={\frac {hL}{k}}

\mathrm {Nu} ={\frac {h}{k/L}}={\frac {hL}{k}}

\mathrm {Nu} ={\frac {h}{k/L}}={\frac {hL}{k}}

k

\mathrm {Nu} ={\frac {h}{k/L}}={\frac {hL}{k}}

\

displaystyle

\

mathrm { Nu

} =

scsfrac

{h

} {

k

/

L}

= scsfrac {hL}

{k

\mathrm {Nu} ={\frac {h}{k/L}}={\frac {hL}{k}}

파생

Nusselt 수는 푸리에의 법칙을 비차원적으로 해석하여 얻을 수 있습니다. 이는 표면의 무차원 온도 구배와 같기 때문입니다.

q=-kA\nabla T

q

=

-

q=-kA\nabla T

q=-kA\nabla T

T {\

displaystyle

q=-

kA\nabla

T

q=-kA\nabla T

여기서 q는 열 전달 속도, k는 일정한 열 전도율, T는 유체

q=-kA\nabla T

입니다.

실제로 다음과 같은 경우: $\nabla '=L\nabla$ $\nabla '=L\nabla$ $∇$ = L \ $displaystyle$ ' $= L$ \ $nabla$ } 및 $\nabla '=L\nabla$ $T'={\frac {T-T_{h}}{T_{h}-T_{c}}}$ $=$ - $T'={\frac {T-T_{h}}{T_{h}-T_{c}}}$ $T'={\frac {T-T_{h}}{T_{h}-T_{c}}}$ $T'={\frac {T-T_{h}}{T_{h}-T_{c}}}$ h - $T'={\frac {T-T_{h}}{T_{h}-T_{c}}}$ \ $displaystyle$ { T - T _ { $h$ } { $displaystyle$ T } { T-T_ { h} { $T_{h}-T_{c}}}}$

도착하다

\displaystyle -\displayla 'T'=displayfrac {L}{kA(T_{h}-T_{c}}}}q=displayfrac {hL}{k}}}

그 후, 정의한다.

\mathrm {Nu} _{L}=black {hL} {k}

그래서 방정식은

\mathrm {Nu} _{L}=-\nabla 'T'

차체 표면에 통합됨:

${\overline {\mathrm {Nu} }}=-{{1} \over {S'}}\int _{S'}^{}\mathrm {Nu} \,\mathrm {d} S'\!$ u ${\overline {\mathrm {Nu} }}=-{{1} \over {S'}}\int _{S'}^{}\mathrm {Nu} \,\mathrm {d} S'\!$ - ${\overline {\mathrm {Nu} }}=-{{1} \over {S'}}\int _{S'}^{}\mathrm {Nu} \,\mathrm {d} S'\!$ S ${\overline {\mathrm {Nu} }}=-{{1} \over {S'}}\int _{S'}^{}\mathrm {Nu} \,\mathrm {d} S'\!$ S ${\overline {\mathrm {Nu} }}=-{{1} \over {S'}}\int _{S'}^{}\mathrm {Nu} \,\mathrm {d} S'\!$ S ${\overline {\mathrm {Nu} }}=-{{1} \over {S'}}\int _{S'}^{}\mathrm {Nu} \,\mathrm {d} S'\!$ Nu d S ${\overline {\mathrm {Nu} }}=-{{1} \over {S'}}\int _{S'}^{}\mathrm {Nu} \,\mathrm {d} S'\!$ { $style$ \ $display$ { ${\overline {\mathrm {Nu} }}=-{{1} \over {S'}}\int _{S'}^{}\mathrm {Nu} \,\mathrm {d} S'\!$ \ $mathrm { Nu$ } } = - { { } \ $over$ { S ' $}$ $}$ } ^{ \ $mathrm { D$ } S \ ${\overline {\mathrm {Nu} }}=-{{1} \over {S'}}\int _{S'}^{}\mathrm {Nu} \,\mathrm {d} S'\!$ 、

$S'={\frac {S}{L^{2}}}$ 서 S $S'={\frac {S}{L^{2}}}$ = $S'={\frac {S}{L^{2}}}$ L $S'={\frac {S}{L^{2}}}$ ({ $displaystyle$ S' $= flac {S}$ { $L^{2$ 입니다.

경험적 상관 관계

일반적으로 자유 대류의 경우, 평균 누셀트 수는 레일리 수와 프란틀 수의 함수로 표현되며, 다음과 같이 표기된다.

\displaystyle \mathrm {Nu} = f(\mathrm {Ra} ,\mathrm {Pr} )

그렇지 않으면 강제 대류의 경우, 누셀트 수는 일반적으로 레이놀즈 수와 프란틀 수의 함수이다.

\displaystyle \mathrm {Nu} = f(\mathrm {Re} ,\mathrm {Pr} )

Nusselt 수를 앞에서 언급한 형태로 표현하는 다양한 기하학에 대한 경험적 상관관계를 사용할 수 있다.

자유 대류

수직벽에서의 자유대류

처칠과^[4]^{: 493} 추에서 인용된 내용:

{\displaystyle {\mathrm {Nu}}_{L}=0.68+{\frac {0.663,\mathrm {Ra}_{L}{\left[1+(0.492/\mathrm {Pr}}{9/16},\right]{4/9}\mathrm}\rmathrm {\rm}\rm}\rm}\rm}\rm {\rm}\rm}\rm}\rm}\rm}\rm {0}\rm

수평판으로부터의 자유 대류

특성 길이가 정의된 경우

L\} = flac {A_{s}} {P}

$\mathrm {A} _{s}$ 서 s $(\displaystyle \mathrm {A} _{$ s $\mathrm {A} _{s}$ })는 플레이트의 $P$ 이고 P $(\displaystyle$ P $)$ 는 $P$ 플레이트의 둘레입니다.

그리고 차가운 환경의 뜨거운 물체의 윗면 또는 뜨거운 환경의^[4]^{: 493} 차가운 물체의 아랫면

{\mathrm {Nu}}_{L}\=0.54,\mathrm {Ra}_{L}{1/4},\quad 10^{4}\leq \mathrm {Ra}_{L}\leq 10^{7

{\mathrm {Nu}}_{L}\=0.15,\mathrm {Ra}_{L}^1/3},\quad 10^{7}\leq \mathrm {Ra}_{L}\leq 10^{11

또한 더 추운 환경의 뜨거운 물체의 바닥 표면 또는 더^[4]^{: 493} 뜨거운 환경의 차가운 물체의 윗 표면도 마찬가지입니다.

{\mathrm {Nu}}_{L}\=0.52,\mathrm {Ra}_{L}^{1/5},\quad 10^{5}\leq \mathrm {Ra}_{L}\leq 10^{10}

평판의 강제 대류

층류 평판

플레이트 가장자리에서 하류 $x$ x $(\displaystyle$ x) $x$ 에 있는 평판 위의 층류용 로컬 Nusselt 번호는 다음과^[4]^{: 490} 같습니다.

\mathrm {Nu} _{x} \mathrm {Re} _{x}^1/2} ,\mathrm {Pr} ^{1/3},(\mathrm {Pr} > 0.6)

플레이트 가장자리에서 다운스트림 $거리$ x $(\displaystyle$ x $x$ 까지의 평판 위의 층류 흐름의 평균 Nusselt 수는 다음과^[4]^{: 490} 같습니다.

{\mathrm {Nu}}_{x}\cdot 0.332,\mathrm {Re}_{x}^1/2},\mathrm {Pr}^{1/3}\0.664,\mathrm {Re}^{{x}^1/2,\mathrm} {pr

대류 중인 구

공기 중의 구형 액체 방울의 증발과 같은 일부 용도에서는 다음과 같은 상관관계가 사용됩니다.^[5]

\mathrm {Nu} _{D} \ = {2} + 0.4 , \mathrm {Re} _{D}^{1/2} , \mathrm { Pr

난류 파이프 흐름의 강제 대류

그닐린스키 상관

튜브의 ^[4]^{: 490, 515}^[6]난류 흐름에 대한 그닐린스키의 상관관계:

\displaystyle \mathrm {Nu} _{D} = phrac {left(f/8\right)\left(\mathrm {Re} _{D}-1000\right)\mathrm {Pr} {1+12.7(f/8)^1/2}\left(\mathrm {Pr} ^2/3/}\right)}}}

여기서 f는 Moody 관리도에서 또는 Petukhov가 ^[4]^{: 490}개발한 상관 관계에서 매끄러운 튜브에 대해 구할 수 있는 Darcy 마찰 계수입니다.

f=\left(0.79\ln \left(\mathrm {Re} _{D}\right)-1.64\right)^{-2

Gnielinski 상관관계는 다음 ^[4]^{: 490}경우에 유효합니다.

0.5\leq\mathrm {Pr}\leq 2000

3000\leq {Re}_{D}\leq 5\times 10^{6}

디투스-볼터 방정식

W.H. McAdams가^[7] 도입한 디투스-보엘터 방정식(난류 흐름용)은 누셀트 수를 계산하기 위한 명시적 함수이다.해결은 쉽지만 유체 전체에서 온도 차이가 큰 경우에는 정확도가 떨어집니다.매끄러운 튜브에 맞게 제작되었으므로 거친 튜브(대부분의 상업적 용도)에 사용할 경우 주의가 필요합니다.디투스-볼터 방정식은 다음과 같다.

\displaystyle \mathrm {Nu} _{D}=0.023,\mathrm {Re} _{D}^4/5},\mathrm {Pr} ^{n}

여기서:

(\displaystyle

D

)

는

D

원형 덕트의 내경입니다.

\mathrm {Pr}

\

displaystyle \mathrm {Pr}

은

\mathrm {Pr}

(

는) Prandtl 번호입니다.

n=0.4

중인

n=0.4

n

n=0.4

0.4

(디스플레이 스타일

n

= 0.4)

이고

n=0.4

, n

n=0.3

0

(디스플레이 스타일

n=

0).

냉각

되는 ^[4]^{: 493}유체에 대하여 3

n=0.3

}.

디투스-볼터 방정식은 다음과 같이 유효하다^[4]^{: 514}.

0.6\leq\mathrm {Pr}\leq 160

\displaystyle \mathrm {Re}_{D}\gtrsim 10,000}

{\displaystyle\frac {L}{D}}\gtrsim 10}

Dittus-Boelter 방정식은 벌크 유체와 열 전달 표면 사이의 온도 차이가 최소인 근사치이며 방정식의 복잡성과 반복 해법을 회피합니다.벌크 유체 평균 온도 20°C(68°F), 점도 10.07×10⁻⁴ Pa.s, 열전달 표면 온도 40°C(104°F)( $점도$ 6. $({\mu }/{\mu _{s}})$ ×10⁻⁴ Pa.s $,$ $mu }/{\mu})$ 의 점도 보정 계수를 1로 얻을 $({\mu }/{\mu _{s}})$ 수 있다.이 값은 100°C(212°F)(점도 2.82⁻⁴×10Pa.)의 열 전달 표면 온도에서 3.57로 증가하며, 누셀트 수와 열 전달 계수에 유의한 차이를 보인다.

Sieder-Tate 상관 관계

더 시더-난류에 대한 테이트 상관관계는 시스템을 비선형 경계값 문제로 분석하기 때문에 암묵적인 함수입니다.더 시더-Tate 결과는 벌크유체 평균온도와 열전달 표면온도의 온도변화에 따른 점도의 변화( $\displaystyle \mu })$ 와 $\mu$ $(\$ _ ${s$ 를 각각 고려하여 보다 정확한 결과를 얻을 수 있다.더 시더-점성 인자는 Nusselt 수가 변화함에 따라 ^[8]변하기 때문에 Tate 상관관계는 일반적으로 반복 프로세스에 의해 해결됩니다.

\displaystyle \mathrm {Nu} _{D}=0.027,\mathrm {Re} _{D}^{4/5},\mathrm {Pr}^{1/3}\leftfrac\frac {{mu}}{\right}^0.14}}}

^[4]^{: 493}

여기서:

\mu

μ

(\displaystyle \mu)

는

\mu

벌크 유체 온도에서의 유체 점도입니다.

\mu _{s}

s \

displaystyle

\

mu

_ {

s}

는

\mu _{s}

열전달 경계 표면 온도에서의 유체 점도입니다.

더 시더-Tate 상관관계가 유효한^[4]^{: 493} 기간:

\displaystyle 0.7\leq \mathrm {Pr} \leq 16,700

\displaystyle \mathrm {Re}_{D}\geq 10,000}

{\displaystyle\frac {L}{D}}\gtrsim 10}

완전히 발달된 층상 파이프 흐름에서 강제 대류

완전히 발달된 내부 층류의 경우 Nusselt 숫자는 긴 파이프에 대해 일정한 값을 갖는 경향이 있습니다.

내부 흐름의 경우:

\mathrm {Nu} = flac {hD_{h}} {k_{f}}

여기서:

D_h = 유압 직경

k_f = 유체의 열전도율

h = 대류 열전달 계수

원형관에서의 균일한 온도에서의 대류

Incropera &^[4]^{: 486–487} DeWitt에서

\displaystyle \mathrm {Nu} _{D} = 3.66}

OEIS 시퀀스 A282581은 이 값을 $\mathrm {Nu} _{D}=3.6567934577632923619...$ $\mathrm {Nu} _{D}=3.6567934577632923619...$ D $\mathrm {Nu} _{D}=3.6567934577632923619...$ 3 $\mathrm {Nu} _{D}=3.6567934577632923619...$ 합니다... ${\displaystyle \mathrm {Nu} _{D}=3.6567934577632923619...$ $\mathrm {Nu} _{D}=3.6567934577632923619...$

원형관용 균일한 열유속 대류

표면 ^[4]^{: 486–487}열 플럭스가 일정할 경우,

\displaystyle \mathrm {Nu} _{D} = 4.36

「」를 참조해 주세요.

레퍼런스

^ ^a ^b ^c ^d Çengel, Yunus A. (2002). Heat and Mass Transfer (2nd ed.). McGraw-Hill.
^ ^a ^b "The Nusselt Number". Whiting School of Engineering. Retrieved 3 April 2019.
^ E. Sanvicente; et al. (2012). "Transitional natural convection flow and heat transfer in an open channel". International Journal of Thermal Sciences. 63: 87–104. doi:10.1016/j.ijthermalsci.2012.07.004.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ Incropera, Frank P.; DeWitt, David P. (2007). Fundamentals of Heat and Mass Transfer (6th ed.). Hoboken: Wiley. ISBN 978-0-471-45728-2.
^ McAllister, Sara; Chen, Jyh-Yuan; Fernández Pello, Carlos (2011). "Droplet Vaporization in Convective Flow". Fundamentals of combustion processes. Mechanical Engineering. New York: Springer. p. 159. doi:10.1007/978-1-4419-7943-8. ISBN 978-1-4419-7942-1. LCCN 2011925371.
^ Gnielinski, Volker (1975). "Neue Gleichungen für den Wärme- und den Stoffübergang in turbulent durchströmten Rohren und Kanälen". Forsch. Ing.-Wes. 41 (1): 8–16. doi:10.1007/BF02559682. S2CID 124105274.
^ Winterton, R.H.S. (February 1998). "Where did the Dittus and Boelter equation come from?" (PDF). International Journal of Heat and Mass Transfer. Elsevier. 41 (4–5): 809–810. doi:10.1016/S0017-9310(97)00177-4.
^ "Temperature Profile in Steam Generator Tube Metal" (PDF). Archived from the original (PDF) on 3 March 2016. Retrieved 23 September 2009.

외부 링크

뉴턴의 냉각 법칙에서 누셀트 수의 단순한 파생(2009년 9월 23일 접근)

[çengel-1] Çengel, Yunus A. (2002). Heat and Mass Transfer (2nd ed.). McGraw-Hill.

[whiting-2] "The Nusselt Number". Whiting School of Engineering. Retrieved 3 April 2019.

[3] E. Sanvicente; et al. (2012). "Transitional natural convection flow and heat transfer in an open channel". International Journal of Thermal Sciences. 63: 87–104. doi:10.1016/j.ijthermalsci.2012.07.004.

[incropera-4] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ Incropera, Frank P.; DeWitt, David P. (2007). Fundamentals of Heat and Mass Transfer (6th ed.). Hoboken: Wiley. ISBN 978-0-471-45728-2.

[5] McAllister, Sara; Chen, Jyh-Yuan; Fernández Pello, Carlos (2011). "Droplet Vaporization in Convective Flow". Fundamentals of combustion processes. Mechanical Engineering. New York: Springer. p. 159. doi:10.1007/978-1-4419-7943-8. ISBN 978-1-4419-7942-1. LCCN 2011925371.

[Gnielinski1975-6] Gnielinski, Volker (1975). "Neue Gleichungen für den Wärme- und den Stoffübergang in turbulent durchströmten Rohren und Kanälen". Forsch. Ing.-Wes. 41 (1): 8–16. doi:10.1007/BF02559682. S2CID 124105274.

[7] Winterton, R.H.S. (February 1998). "Where did the Dittus and Boelter equation come from?" (PDF). International Journal of Heat and Mass Transfer. Elsevier. 41 (4–5): 809–810. doi:10.1016/S0017-9310(97)00177-4.

[8] "Temperature Profile in Steam Generator Tube Metal" (PDF). Archived from the original (PDF) on 3 March 2016. Retrieved 23 September 2009.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Search

누셀트 수

네임스페이스

더

목차

정의.

맥락

파생