들어올리기(힘)

물체의 표면을 흐르는 액체는 물체에 힘을 가한다. 리프트는 다가오는 흐름 방향에 수직인 이 힘의 구성요소다.^[1] 흐름 방향에 평행한 힘의 구성요소인 드래그 힘과 대비된다. 리프트는 전통적으로 중력에 대항하기 위해 위쪽으로 작용하지만 흐름과 직각으로 어떤 방향으로도 작용할 수 있다.

주변 액체가 공기일 경우 그 힘을 공기역학적 힘이라고 한다. 물이나 다른 액체에서는 유체역동력이라고 불린다.

동적 리프트는 액체의 다른 종류의 리프트와 구별된다. 내부 액체가 주변 액체에 비해 가벼워 이동이 필요 없고 풍선, 블림프, 비행선, 보트, 잠수함 등이 사용한다. 차체의 아랫부분만 액체 흐름에 담그는 평면 리프트는 모터보트, 서프보드, 윈드서퍼, 돛단배, 수상스키 등이 사용한다.

개요

고체 물체의 표면 둘레를 흐르는 액체는 그 물체에 힘을 가한다. 물체가 고정된 유체(예: 공중을 비행하는 항공기)를 통해 움직이는지, 물체가 정지해 있고 유체가 움직이는지(예: 풍동 안의 날개) 또는 둘 다 움직이는지(예: 바람을 이용하여 앞으로 나아가는 범선)는 중요하지 않다. 리프트는 다가오는 흐름 방향에 수직인 이 힘의 구성요소다.^[1] 리프트는 항상 흐름 방향에 평행한 표면 힘의 구성요소인 드래그 하중을 동반한다.

리프트는 프로펠러, 연, 헬리콥터 로터, 경주용 자동차 날개, 해상 돛, 풍력 터빈과 같은 많은 다른 유선형 몸체들과 범선 켈, 배의 방향타, 물속의 수력 포에 의해 더 널리 생성되지만 대부분 고정익 항공기의 날개와 연관되어 있다. 리프트는 또한 날고 미끄러지는 동물, 특히 새, 박쥐, 곤충에 의해서도 사용되며, 심지어 식물 세계에서도 특정 나무의 씨앗에 의해서도 사용된다.^[2] '리프트'라는 말의 공통적인 의미는 리프트가 무게에 반대한다고 가정하는 반면, 리프트는 무게의 방향이 아닌 흐름의 방향에 대해 정의되기 때문에 중력에 관해서라면 어떤 방향에도 있을 수 있다. 항공기가 직진 및 수평 비행을 할 때 대부분의 리프트는 중력에 반대한다.^[3] 그러나 항공기가 상승, 하강 또는 뱅킹할 때 리프트는 수직에 대해 기울어진다.^[4] 리프트는 또한 일부 곡예비행 또는 경주용 자동차의 날개에서 다운포스 역할을 할 수 있다. 리프트는 예를 들어 범선 위에서는 대체로 수평이 될 수 있다.

이 글에서 논하는 리프트는 밀도, 압축성, 점도와 같은 공기와 물의 차이에도 불구하고 해양 수력포와 프로펠러는 동일한 물리적 원리를 공유하고 동일한 방식으로 작동하지만 주로 에어포일과 관련된다.

리프팅 에어포일 주위의 흐름은 기본적으로 두 가지 수준에서 이해할 수 있는 유체역학 현상이다. 수학 이론이 있는데, 수학 이론은 확립된 물리 법칙에 기초하여 흐름을 정확하게 나타내지만, 부분 미분 방정식을 풀어야 한다. 그리고 수학이 없는 물리적인 설명도 있는데, 그것은 덜 엄격하다.^[5] 관련된 인과관계가 미묘하기 때문에 이러한 질적 측면에서 리프트를 올바르게 설명하는 것은 어렵다.^[6] 본질적인 측면을 모두 포착한 종합적인 설명은 반드시 복잡하다. 또한 간단한 설명도 많지만, 모두 현상의 중요한 부분을 설명하지 못한 채 방치하고 있는 반면, 일부 또한 단순히 부정확한 요소를 지니고 있다.^{[7][8][9][10][11][12]}

에어포일 리프트에 대한 간단한 물리적 설명

에어포일은 드래그보다 훨씬 더 많은 양력을 발생시킬 수 있는 유선형이다.^[13] 평평한 판은 양력을 발생시킬 수 있지만, 능률화된 에어포일만큼 많지는 않으며, 드래그도 다소 높다. 가장 간단한 설명은 뉴턴의 운동 법칙이나 베르누이의 원리에 기초하여 두 가지 기본적인 접근법 중 하나를 따른다.^{[14][15][16][17]}

흐름 편향 및 뉴턴의 법칙에 근거한 설명

에어포일은 공기 중에 아래로 흐르는 힘을 작용하여 양력을 발생시킨다. 뉴턴의 제3법칙에 따르면 공기는 에어포일(양력)에 동일하고 반대(상향)의 힘을 발휘해야 한다.^{[18][19][20][21]}

기류는 에어포일을 지나 아래로 굽은 길을 따라 방향을 바꾼다. 뉴턴의 제2법칙에 따르면, 이러한 흐름 방향의 변화는 공기포에 의해 공기에 가해지는 하방력을 필요로 한다. 그 후 뉴턴의 제3법칙은 공기가 공기포일에 상승력을 발휘하도록 요구한다. 따라서 방향 변화에 반대되는 반작용력인 양력이 발생한다. 비행기 날개의 경우 날개는 공중에서 아래쪽으로 힘을 발휘하고 공기는 날개에 위쪽으로 힘을 발휘한다.^{[22][23][24][25][26][27]}

흐름의 하향 전환은 에어포일의 하부 표면만으로 이루어지는 것이 아니며, 에어포일 위의 공기 흐름은 하강 턴 작용의 상당 부분을 차지한다.^{[28][29][30][31]}

이 설명은 정확하지만 불완전하다. 그것은 어떻게 에어포일이 실제 접촉하는 것보다 훨씬 더 깊은 흐름의 흐름으로 아래쪽으로 방향을 바꿀 수 있는지 설명하지 못한다. 게다가, 그것은 리프트 힘이 압력 차이에 의해 발휘된다는 것을 언급하지 않으며, 그러한 압력 차이가 어떻게 지속되는지를 설명하지 않는다.^[17]

코안데르 효과 논란

리프트의 흐름 편향 설명의 일부 버전은 흐름이 에어포일의 볼록한 상부 표면을 따를 수 있는 이유로 Coandand 효과를 인용한다. 공기역학 분야에서 일반적인 정의는 Coandă 효과란 유체 제트가 흐름으로부터 멀리 구부러지는 인접 표면에 부착되어 있고, 그 결과 주변 공기가 흐름으로 유입되는 경향을 가리킨다.^[32][33][34]

보다 광범위하게, 일부 사람들은 유체 분사물에 수반되는 경계층만이 아니라 곡선 표면에 부착되는 유체 경계층의 경향을 포함하는 효과를 고려한다. 이러한 넓은 의미에서 Coandand 효과는 왜 공기 흐름이 에어포일 상면에 부착되어 있는지 설명하기 위해 몇몇 인기 있는 언급에 의해 이용된다.^[35][36] 이것은 "Coandă effect"라는 용어의 논란의 여지가 있는 용어로, 상부 표면을 따르는 흐름은 단순히 경계층 분리의 부재를 반영하기 때문에 Coand effect 효과의 예가 아니다.^{[37][38][39][40]}

유속 증가와 베르누이의 원리에 근거한 설명

이 설명에는 두 가지 공통 버전이 있는데, 하나는 "동일한 운송 시간"에 근거한 것이고, 하나는 공기 흐름의 "방해"에 근거한 것이다.

동일한 운송 시간에 근거한 거짓 설명

"동일한 운송 시간" 설명은 상면 위의 경로 길이가 더 길기 때문에 상면 위의 흐름이 하면 위의 흐름보다 더 빠르며, 동일한 운송 시간에 통과해야 한다는 주장에서 시작된다.^[41][42][43] 베르누이의 원칙은 특정 조건에서 증가된 유속은 압력 감소와 관련이 있다고 말한다. 상부 표면에 대한 압력이 감소하면 상향 양력이 발생한다는 결론이 내려진다.^[44]

동등한 운송 시간 설명의 심각한 결함은 흐름의 속도를 높이는 원인이 무엇인지 정확하게 설명하지 못한다는 것이다.^[17] 길쭉한 설명은 그야말로 잘못된 것이다. 경로 길이의 차이는 필요하지 않으며, 차이가 있을 때에도 일반적으로 관측된 속도 차이를 설명하기에는 너무 작다.^[45] 동일 환승시간이라는 가정이 잘못됐기 때문이다. 동일한 운송 시간을 요구하는 물리적 원리는 없으며 실험 결과는 이 가정이 거짓임을 보여준다.^{[46][47][48][49][50][51]} 사실, 리프트를 발생시키는 에어포일 꼭대기로 이동하는 공기는 동일한 운송 이론이 예측하는 것보다 훨씬 더 빠르게 움직인다.^[52] 상부 표면에 비해 훨씬 높은 유속은 에어포일 주위의 더 넓은 흐름과 인접한 애니메이션 흐름 시각화에서 명확하게 볼 수 있다.

공기 흐름 방해

동등한 운송시간 설명과 마찬가지로 '오브러시'나 '스트림튜브 꼬집기' 설명은 상면 위의 흐름이 하면 위의 흐름보다 빠르다고 주장하지만, 속도 차이가 나는 이유는 다르다. 굽은 상부 표면이 흐름에 더 큰 장애물로 작용해 스트림선이 서로 더 가까이 붙을 수밖에 없어 하천관이 좁아진다는 것이다. 하천관이 좁아지면 질량을 보전하려면 유속이 빨라져야 한다.^[53] 상층부 압력 감소와 상향 리프트는 동일한 운송 시간 설명에서와 마찬가지로 베르누이의 원리에 의해 더 높은 속도에서 따라온다. 간혹 벤투리 노즐에 비유하여 날개 윗면이 베누리 노즐처럼 작용하여 흐름을 수축시킨다고 주장하기도 한다.^[54]

장애물 설명의 한 가지 심각한 결함은 스트림튜브 핀칭이 어떻게 발생하는지, 또는 왜 아래쪽 표면보다 위쪽 표면에 더 큰지 설명하지 않는다는 것이다. 하단에 평평하고 위에서 구부러진 재래식 날개의 경우 이것은 직관적인 의미를 갖지만, 평평한 판, 대칭형 에어포일, 범선 돛 또는 거꾸로 날아가는 재래식 에어포일이 어떻게 양력을 발생시킬 수 있는지 설명하지 않으며, 수축이나 방해물의 양에 기초하여 양력을 계산하려는 시도는 실험적으로 예측하지 않는다.결실을 ^{[55][56][57][58]}거두다 또 다른 결점은 질량을 보존하는 것이 흐름이 빨라지는 만족스러운 물리적 이유가 아니라는 것이다. 어떤 것이 속도를 내는 이유를 정말로 설명하려면 그것을 가속시키는 힘을 식별해야 한다.^[59]

버누이 기반 설명의 두 버전 모두에 공통적인 문제

베르누이에 근거한 모든 설명에 공통적으로 나타나는 심각한 결함은 속도 차이가 압력차 이외의 원인에 의해 발생할 수 있음을 암시하고, 그 후 속도차가 압력차이로 이어진다는 것을 버누이의 원리에 의해 암시한다는 것이다. 이 암묵적인 일방향 인과관계는 잘못된 생각이다. 압력과 유속 사이의 진정한 관계는 상호 상호작용이다.^[17] 보다 포괄적인 물리적 설명에 따라 아래에 설명했듯이, 리프트 힘을 생성하려면 수직 방향과 수평 방향 모두에서 압력 차이를 유지해야 한다. 베르누이만의 설명은 수직 방향의 압력 차이가 어떻게 지속되는지 설명하지 않는다. 즉, 상호작용의 흐름-편향 부분을 배제한다.^[17]

위의 두 가지 간단한 베르누이에 근거한 설명은 틀리지만, 베르누이의 원리나 날개 위에서 공기가 더 빨리 간다는 사실에는 틀린 것이 없으며, 베르누이의 원리는 리프트에 대한 좀 더 복잡한 설명의 일환으로 정확하게 사용될 수 있다.^[60]

리프트의 기본 속성

리프트는 압력 차이의 결과물이며 공격 각도, 에어포일 형태, 공기 밀도, 비행 속도에 따라 달라진다.

압력차이

압력은 공기에 의해 그 자체와 그것이 닿는 표면에 가해지는 단위 면적당 일반적인 힘이다. 리프트 힘은 압력을 통해 전달되며, 이 압력은 에어포일 표면에 수직으로 작용한다. 따라서 순력은 압력 차이로 나타난다. 순력의 방향은 에어포일 상부 표면의 평균 압력이 아래쪽의 평균 압력보다 낮다는 것을 의미한다.^[61]

이러한 압력 차이는 곡선 기류와 함께 발생한다. 유체가 곡선 경로를 따라갈 때, 곡선 외부는 높은 압력으로, 내부는 낮은 압력으로 흐름 방향에 수직인 압력 구배가 있다.^[62] 능률적인 곡률 정리라고도 불리는 곡선 흐름과 압력 차이 사이의 직접적인 관계는 1754년 레온하르트 오일러에 의해 뉴턴의 제2법칙에서 유래되었다.

${\displaystyle {\frac {\d}p}{\operatorname {d}R}=\rho {\frac {v^{2}}{R}}}}$

이 방정식의 왼쪽은 유체 흐름에 수직인 압력 차이를 나타낸다. 오른쪽 ρ은 밀도, v는 속도, R은 곡률 반경이다. 이 공식은 더 높은 속도와 더 촘촘한 곡선들이 압력 차이를 더 크게 만들고 직류(R → ∞)의 압력 차이가 0이라는 것을 보여준다.^[63]

공격 각도

공격 각도는 에어포일의 현선과 다가오는 기류 사이의 각도다. 대칭적인 에어포일은 공격 각도에서 제로 리프트를 생성한다. 그러나 공격 각도가 높아질수록 공기는 더 큰 각도로 꺾이고 기류 속도의 수직 성분이 증가하여 더 많은 양력을 얻는다. 작은 각도에서 대칭 공포는 공격 각도에 대략 비례하는 상승력을 생성한다.^[64][65]

공격 각도가 증가함에 따라 리프트는 어느 각도에서 최대치에 도달한다; 공격의 임계 각도를 넘어 공격 각도를 증가시키면 상부 표면 흐름이 날개에서 분리된다; 아래로 처짐이 적어 에어포일이 리프트를 덜 발생시킨다. 에어포일이 멈춰 있다고 한다.^[66]

에어포일 모양

주어진 비행속도에서 에어포일에 의해 발생할 수 있는 최대 상승력은 에어포일의 형태, 특히 캠버의 양(오른쪽 그림처럼 상부 표면이 하부 표면보다 볼록하게 되는 곡선)에 따라 달라진다. 캠버를 증가시키면 일반적으로 주어진 비행 속도에서 최대 리프트가 증가한다.^[67][68]

캠베어링된 에어포일은 공격 각도가 0일 때 리프트를 발생시킨다. 현선이 수평일 때, 후행 가장자리는 하향 방향을 가지며, 공기가 후행 가장자리를 따르므로 후행 가장자리는 아래로 꺾인다.^[69] 캠베어링된 에어포일이 뒤집혀 있을 때 공격 각도를 조절해 상승력이 위로 올라오게 할 수 있다. 이것은 비행기가 어떻게 거꾸로 날 수 있는지를 설명해준다.^[70][71]

흐름 조건

리프트에 영향을 미치는 주변 유량 조건에는 유체 밀도, 점도 및 유속 등이 포함된다. 밀도는 온도와 매체의 음향 속도(즉, 압축성 효과)에 의해 영향을 받는다.

공기 속도 및 밀도

리프트는 공기의 밀도에 비례하고 흐름 속도의 제곱에 대략 비례한다. 리프트는 또한 날개 크기에 따라 달라지는데, 일반적으로 리프트 방향으로 투영된 날개 면적에 비례한다. 계산에서 이러한 요인에 기초한 리프트 계수의 관점에서 리프트를 정량화하는 것이 편리하다.

경계 도면층 및 종단 드래그

아무리 에어포일 표면이 매끈해 보여도 공기 분자 규모로 보면 어떤 표면도 거칠다. 표면으로 날아드는 공기 분자는 원래 속도에 비례하여 거친 표면에서 무작위로 튕겨 나간다. 그 결과 공기를 연속 물질로 볼 때 표면을 따라 미끄러질 수 없는 것으로 보이며, 에어포일에 상대적인 공기의 속도는 표면에서 거의 0(즉, 공기 분자가 미끄러지지 않고 표면에 "붙는" 것), 즉 미끄러지지 않는 상태로 알려져 있다.^[72] 표면의 공기는 속도가 거의 0에 가깝지만 표면에서 멀리 떨어진 공기는 움직이고 있기 때문에, 표면에 가까운 공기가 피복 운동을 하는 얇은 경계층이 있다.^[73][74] 공기의 점도는 칼집을 억제하여 피부 마찰 드래그라고 불리는 에어포일 표면에 전단 응력을 일으킨다. 대부분의 에어포일 표면에서 경계층은 자연적으로 난류하여 피부 마찰 항력을 증가시킨다.^[74][75]

통상적인 비행 조건에서 경계층은 후행 가장자리까지 위쪽과 아래쪽 표면 모두에 부착되어 있으며, 그 영향이 나머지 유동에 미치는 영향은 미미하다. 경계층이 없는 비점성 유동 이론의 예측에 비해 부착된 경계층은 리프트를 다소 줄이고 압력 분포를 다소 수정하여 피부 마찰 드래그 위와 위쪽으로 점도와 관련된 압력 드래그를 유발한다. 피부 마찰 드래그와 점성 관련 압력 드래그의 합계를 보통 프로필 드래그라고 한다.^[75][76]

Stating

주어진 비행 속도에서 비행포일의 최대 양력은 경계층 분리에 의해 제한된다. 공격 각도가 높아짐에 따라 경계층이 더 이상 상부 표면에 붙어 있을 수 없는 지점에 도달하게 된다. 경계층이 분리되면 오른쪽의 흐름 시각화 사진에서와 같이 상부 표면 위로 재순환되는 흐름의 영역을 남긴다. 이것을 노점, 즉 정지라고 한다. 스톨 위에서의 공격 각도에서 리프트는 0으로 떨어지지는 않지만 현저하게 감소한다. 정지 전에 달성할 수 있는 최대 리프트는 리프트 계수에 있어 단일 요소 에어포일의 경우 일반적으로 1.5 미만이며, 높은 리프트 슬롯형 플랩과 최첨단 장치가 배치된 에어포일의 경우 3.0 이상일 수 있다.^[77]

허풍쟁이 몸

허세를 부리는 몸체 주위의 흐름(즉, 유선형 형태가 없거나 에어포일을 정지시키는 것)은 강한 드래그 힘 외에 양력을 발생시킬 수도 있다. 이 리프트는 안정적이거나 소용돌이 드리핑으로 인해 진동할 수 있다. 물체의 유연성과 볼텍스 드리핑의 상호작용으로 인해 들썩이는 리프트의 효과가 향상되고 볼텍스 유도 진동이 발생할 수 있다.^[78] 예를 들어, 원형 실린더 주위의 흐름은 카르만 소용돌이의 거리를 생성하는데, 그것은 실린더의 측면에서 교대로 흘리는 것이다. 흐름의 진동 특성은 순(평균)의 힘이 무시할 수 있음에도 불구하고 실린더에 변동하는 상승력을 생성한다. 리프트 힘 주파수는 흐름의 레이놀즈 수에 따라 달라지는 무차원 스트라우할 숫자로 특징지어진다.^[79][80]

유연한 구조물의 경우, 이 진동 상승력은 소용돌이에 의한 진동을 유발할 수 있다. 예를 들어, 리프트 하중의 공진 또는 강한 스팬와이드 상관관계와 같은 특정 조건에서는 리프트 변동에 의한 구조물의 움직임이 강하게 증가할 수 있다. 그러한 진동은 산업용 굴뚝과 같은 높은 인공 구조물에 문제를 일으킬 수 있고 붕괴를 위협할 수 있다.^[78]

마그누스 효과에서, 리프트 힘은 프리스트림에서 회전하는 실린더에 의해 발생한다. 여기서 기계적 회전이 경계층에 작용하여 실린더의 양쪽에 있는 서로 다른 위치에서 분리되게 한다. 비대칭 분리는 유량에 관한 한 원통의 유효 형태를 변화시켜 원통이 외부 유동에 순환이 있는 리프팅 에어포일처럼 작용한다.^[81]

보다 포괄적인 물리적 설명

위에서 설명한 "공기포 리프트의 간단한 물리적 설명"에 따르면, 두 가지 주요 인기 설명이 있는데, 하나는 흐름의 하향 편향에 근거한 것(뉴턴의 법칙), 하나는 흐름 속도의 변화에 수반하는 압력 차이에 근거한 것(베르누엘리의 원리)이다. 이들 중 어느 하나라도 그 자체로 리프팅 흐름의 일부 측면을 정확하게 식별하지만 현상의 다른 중요한 측면은 설명되지 않는다. 보다 포괄적인 설명은 하향 편향과 압력 차이(압력 차이와 관련된 흐름 속도의 변화 포함)를 모두 포함하며, 흐름을 보다 자세히 살펴볼 필요가 있다.^[82]

에어포일 표면에서 들어올리기

에어포일 형태와 공격 각도가 함께 작용하여 에어포일이 흘러갈 때 공기에 하강력을 발휘한다. 뉴턴의 제3법칙에 따르면, 공기는 이때 리프트인 에어포일에 동등하고 반대(위쪽)의 힘을 발휘해야 한다.^[20]

공기에 의해 발휘되는 순 힘은 에어포일 표면에 대한 압력 차이로 발생한다.^[83] 유체의 압력은 절대적 의미에서는 항상 양성이므로,^[84] 압력은 항상 밀고 당기는 것으로 생각되어야 하며, 결코 당기는 것으로 생각되어서는 안 된다. 따라서 압력은 상면과 하단의 모든 곳에 있는 에어포일을 안쪽으로 밀어 넣는다. 흐르는 공기는 날개 윗면의 압력을 줄이고 아랫면의 압력을 증가시킴으로써 날개의 존재에 반응한다. 낮은 표면의 압력은 낮은 표면의 압력이 낮아지는 것보다 더 강하게 위로 밀어올리고, 그 순 결과는 위로 상승하는 것이다.^[83]

리프트가 발생하는 압력 차이는 에어포일 표면에 직접 작용하지만, 압력 차이가 어떻게 생성되는지 이해하려면 더 넓은 영역에 걸쳐 흐름이 무엇을 하는지 이해해야 한다.

에어포일 주위의 넓은 흐름

에어포일은 넓은 지역에 걸쳐 흐름의 속도와 방향에 영향을 주어 속도장이라고 불리는 패턴을 생성한다. 에어포일이 리프트를 생성하면 에어포일 앞의 흐름이 위쪽으로 꺾이고 에어포일 위아래로 꺾이며 에어포일 뒤의 흐름이 다시 위쪽으로 꺾이면서 훨씬 앞쪽으로 다가오는 흐름과 같은 상태로 공기가 에어포일 뒤쪽으로 꺾인다. 상부 표면 위의 흐름은 속도를 높이는 반면, 에어포일 아래의 흐름은 느려진다. 이것은 앞쪽의 공기의 상향 편향과 바로 뒤의 하향 편향과 함께 흐름의 순 순환 구성요소를 설정한다. 오른쪽의 흐름 애니메이션에서 볼 수 있듯이 하향 편향과 흐름 속도의 변화가 뚜렷하고 넓은 영역에 걸쳐 확장된다. 흐름의 방향과 속도의 이러한 차이는 에어포일에 가장 가깝고 위아래로 점차 감소한다. 속도장의 이러한 모든 특성은 리프팅 흐름을 위한 이론적 모델에도 나타난다.^[85][86]

압력은 또한 넓은 지역에 걸쳐서 압력장이라고 불리는 불균일한 압력의 패턴으로 영향을 받는다. 에어포일이 리프트를 생성할 때, 에어포일 위쪽에 저압의 확산 영역이 있고, 일반적으로 도면의 이소바(일정압의 곡선)에서 예시한 바와 같이 아래 고기압의 확산 영역이 있다. 표면에 작용하는 압력차는 단지 이 압력장의 일부일 뿐이다.^[87]

압력 차이 및 유속 변화의 상호 작용

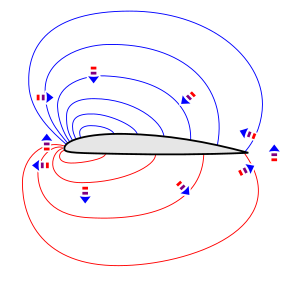
균일하지 않은 압력은 높은 압력에서 낮은 압력으로 가는 방향으로 공기에 힘을 발휘한다. 힘의 방향은 에어포일 그림 주위의 압력장에 있는 블록 화살표로 나타내듯이 에어포일 주위의 다른 위치에서 다르다. 에어포일 위쪽의 공기는 저기압 지역 중앙을 향해 밀리고, 에어포일 아래쪽의 공기는 고기압 지역 중앙에서 바깥쪽으로 밀린다.

뉴턴의 두 번째 법칙에 따르면, 힘은 공기의 방향에서 가속을 일으킨다. 따라서 수반되는 압력장 다이어그램의 수직 화살표는 에어포일 위와 아래의 공기가 가속되거나 아래로 회전한다는 것을 나타내며, 따라서 균일하지 않은 압력이 흐름 애니메이션에서 보이는 흐름의 하향 편향의 원인임을 나타낸다. 이러한 하향 회전을 생성하기 위해, 에어포일은 양의 공격 각도를 가지거나 충분한 양의 캠버를 가져야 한다. 상부 표면 위로 유량이 아래로 회전하는 것은 공기가 그 아래보다 높은 압력에 의해 아래로 밀려 내려가는 결과라는 점에 유의한다. '코앤드루션 효과'를 언급하는 일부 설명은 점성이 하향 전환에 핵심적인 역할을 한다는 점을 시사하지만 이는 거짓이다. (아래 "Coanduff 효과에 대한 논쟁" 참조).

에어포일 앞의 화살표는 에어포일 앞의 흐름이 위쪽으로 꺾여 있음을 나타내며, 에어포일 뒤의 화살표는 에어포일 위로 아래로 꺾인 후 다시 위쪽으로 꺾여 있음을 나타낸다. 이러한 편향은 플로우 애니메이션에서도 볼 수 있다.

또한 에어포일 앞과 뒤쪽의 화살표는 에어포일 위 저기압 지역을 통과하는 공기가 들어갈 때 속도를 높이고, 에어포일이 떠날 때 속도를 늦춘다는 것을 나타낸다. 에어포일 아래 고기압 지역을 통과하는 공기는 공기 유입이 느려졌다가 출발하면서 다시 속도를 낸다. 따라서 균일하지 않은 압력도 흐름 애니메이션에서 볼 수 있는 흐름 속도 변화의 원인이다. 유속 변화는 점성이 없는 꾸준한 흐름에서 압력이 낮으면 속도가 더 빨라지고, 압력이 높을수록 속도가 더 낮아진다는 베르누이의 원칙과 일치한다.

따라서 흐름 방향과 속도의 변화는 균일하지 않은 압력에 의해 직접적으로 발생한다. 그러나 이 인과관계는 일방통행이 아니라 양방향으로 동시에 작용한다. 공기의 움직임은 압력 차이에 의해 영향을 받지만, 압력 차이의 존재는 공기의 움직임에 따라 달라진다. 따라서 이 관계는 상호 또는 상호 작용이다. 공기 흐름은 압력 차이에 대응하여 속도나 방향을 변경하며, 압력 차이는 속도나 방향 변화에 대한 공기의 저항에 의해 지속된다.^[88] 압력차이는 그것이 밀어낼 무언가가 있어야만 존재할 수 있다. 공기역학적 흐름에서 압력차는 공기의 관성을 밀어낸다. 압력차에 의해 공기가 가속되기 때문이다.^[89] 공기의 질량이 계산의 일부인 이유, 그리고 왜 양력이 공기 밀도에 따라 달라지는가 하는 이유가 바로 여기에 있다.

에어포일 표면에서 리프트 힘을 발휘하는 압력 차이를 유지하려면 에어포일 주위의 넓은 영역에서 균일하지 않은 압력 패턴을 유지해야 한다. 이를 위해서는 수직 방향과 수평 방향 모두에서 압력 차이를 유지해야 하므로 베르누이의 원칙에 따라 유량의 하향 회전과 유속 변화를 모두 필요로 한다. 압력 차이와 흐름 방향과 속도의 변화는 상호 상호작용에서 서로를 지탱한다. 압력 차이는 뉴턴의 두 번째 법칙과 표면을 따라 흐르는 흐름이 주로 아래쪽으로 기울어진 에어포일의 등고선을 따른다는 사실에서 자연스럽게 나타난다. 그리고 공기에 질량이 있다는 사실이 상호작용에 결정적이다.^[90]

얼마나 간단한 설명이 부족한가.

리프트 힘을 생산하려면 유량의 하향 회전과 베르누이의 원리에 부합하는 유속의 변화가 모두 필요하다. 에어포일 리프트에 대한 단순화된 물리적 설명에서 위에 제시된 각각의 단순화된 설명은 리프트를 한 가지 또는 다른 한 가지 측면에서만 설명하려고 하면 부족하기 때문에 현상의 일부만 설명하고 다른 부분은 설명되지 않는다.^[91]

양적 리프트

압력집적

에어포일 표면의 압력 분포를 알 수 있는 경우, 전체 리프트를 결정하려면 각각 고유한 압력 값을 갖는 표면의 국소 요소로부터 압력력에 대한 기여를 추가해야 한다. 따라서 총 리프트는 공기포일 표면 위의 원야 유량에 수직인 방향에서 압력의 일체형이다.^[92]

${\displaystyle L=\point p\mathbf {n} \cdot \mathbf {k} \;\mathrm {d}S,}$

여기서:

• S는 에어포일의 투사(planform) 영역이며, 평균 기류에서 정상으로 측정된다.
• n은 날개를 가리키는 정상 단위 벡터;
• k는 수직 단위 벡터로서, 프리스트림 방향에서 정상이다.

위의 리프트 방정식은 압력력에 비해 작은 피부 마찰력을 무시한다.

적분에서 k 대신 freestream에 평행한 스트림와이즈 벡터 i를 사용함으로써 압력 드래그 D_p(프로파일 드래그의 압력 부분과 날개가 3차원인 경우 유도 드래그)에 대한 식을 얻는다. 스팬와이즈 벡터 j를 사용하면 측면력 Y를 얻는다.

${\displaystyle {\reasoned}D_{p}&=\cd p\mathbf {n} \cdot \mathbf {i} \;\mathbf {d}S,\Y&=\point p\mathbf {n} \cdot \mathbf {j} \d}S.\{igned}}}}}}}}}$

이 통합의 유효성은 일반적으로 에어포일 모양이 조각처럼 매끄러운 닫힌 곡선이어야 한다.

리프트 계수

리프트는 날개 크기에 따라 달라지며, 날개 면적에 거의 비례한다. 특정 에어포일의 양력을 날개 단위 면적 관점에서 전체적인 양력을 정의하는 리프트 계수 ${\displaystyle C_{}}$ L${\$에 의해 정량화하는 것이 편리하다$.$

특정 공격 각도에서의 날개에 대한$$ $C{\displaystyle {}_{}}$ ${\displaystyle L_{}}$ ${\$의 값이 주어진 경우 특정 흐름 조건에 대해 생성된 리프트를 결정할 수 있다.^[93]

${\displaystyle L={\tfrac {1}{1}{2}}\rho v^{2}SC_{L}}$

어디에

• ${\displaystyle L}$ ${\displaystyle L}$은(는) 리프트 힘이다.
• ${\displaystyle \rho }$ ${\displaystyle \rho}$은(는) 공기 밀도
• ${\displaystyle v}$ ${\displaystyle v}$은(는) 속도 또는 실제 비행 속도임
• ${\displaystyle S}$ ${\displaystyle S}$은 평면형(투사된) 날개 영역이다.
• ${\displaystyle C_{}}$ ${\displaystyle L_{}}$ ${\$는 원하는 공격 각도, 마하 수, 레이놀즈 수에서의^[94] 리프트 계수다$$.

리프트의 수학 이론

수학적 리프트 이론은 공기가 연속 유체로 흐른다고 가정할 때 연속 유체 역학에 기초한다.^[95][96][97] 리프트는 물리학의 기본 원리에 따라 생성되며, 가장 관련성이 높은 세 가지 원리는 다음과 같다.^[98]

• 운동량의 보존, 이것은 뉴턴의 운동 법칙, 특히 공기의 원소에 대한 순 힘과 운동량의 변화 속도를 연관시킨 뉴턴의 두 번째 법칙의 결과물이다.
• 공기의 표면이 공기의 흐름을 방해할 수 없다는 가정을 포함한 질량의 보존
• 에너지가 생성되거나 파괴되지 않는다고 말하는 에너지의 보존.

에어포일은 주변의 넓은 영역의 흐름에 영향을 미치기 때문에, 역학의 보존 법칙은 흐름이 에어포일 표면에서 멀리 떨어진 곳에서 충족시켜야 하는 일련의 경계 조건 요건과 결합된 부분 미분 방정식의 형태로 구체화된다.^[99]

양력을 예측하려면 특정 에어포일 형태와 흐름 조건에 대한 방정식을 풀어야 하는데, 일반적으로 계산 유체 역학(CFD)의 방법을 통해 컴퓨터에서만 실용적일 정도로 부피가 큰 계산이 필요하다. CFD 용액에서 순 공기역학적 힘을 결정하려면 "압력 통합"에 따라 설명한 대로 에어포일의 모든 표면 요소에 대해 CFD에 의해 결정된 압력과 전단 때문에 힘을 "추가"(통합)해야 한다.

더 나비에–스톡스 방정식(NS)은 잠재적으로 가장 정확한 리프트 이론을 제공하지만, 실제로는 경계층의 난류 효과를 에어포일 표면에 포착하려면 어느 정도 정확성을 희생해야 하며, 레이놀즈-평균 나비에를 사용해야 한다.–스토크 방정식(RANS). 단순하지만 정확도가 떨어지는 이론도 개발됐다.

Navier-Stokes(NS) 방정식

이 방정식은 질량 보존, 뉴턴의 제2법칙(운동량 보존), 에너지 보존, 점도의 작용을 위한 뉴턴법, 푸리에 열전도율법, 밀도, 온도 및 압력과 관련된 상태 방정식, 유체의 점도와 열전도율에 대한 공식 등을 나타낸다.^[100][101]

원칙적으로 NS 방정식은 공기포일 표면에서 관통 유량이 없고 미끄러짐이 없는 경계 조건과 결합하여 일반 대기 비행의 어떤 상황에서도 높은 정확도로 양력을 예측할 수 있다. 그러나 실제 상황에서의 기류는 항상 적어도 에어포일의 후면에서 에어포일 표면 옆에 있는 경계층의 난류를 수반한다. 원시 형태로 NS 방정식을 풀어서 양력을 예측하는 것은 난류의 세부사항을 해결하기 위한 계산이 필요할 것이다. 이것은 현재 가장 강력한 컴퓨터에서도 아직 가능하지 않다.^[102] 따라서 원칙적으로 NS 방정식은 완전하고 매우 정확한 리프트 이론을 제공하지만, 리프트의 실제적인 예측은 난류의 영향을 직접 계산하는 것이 아니라 RANS 방정식에 모델링할 것을 요구한다.

레이놀즈-평균 나비에르–스톡스(RANS) 방정식

이는 시간 경과에 따른 난류 운동을 평균화한 NS 방정식과 난류 모델링으로 대표되는 시간 평균 흐름에 대한 난류의 영향(시간 평균적 의미에서의 난류가 경계 층에 미치는 영향에 대한 치수 분석과 경험적 정보의 조합에 기초한 추가 방정식 집합)이다.RANS 용액은 에어포일을 둘러싼 점의 밀집 격자에서 정의된 시간 평균 속도 벡터, 압력, 밀도 및 온도로 구성된다.^[103][104]

필요한 계산량은 원시 NS 계산에서 모든 난류 운동을 해결하는 데 필요한 양의 극히 일부(억분의 1)^[102]이며, 대형 컴퓨터를 사용할 수 있게 되어 이제 3차원의 완전한 비행기에 대해 RANS 계산을 수행하는 것이 실용적이다. 난류 모델이 완벽하지 않기 때문에 RANS 계산의 정확도는 불완전하지만 실제 항공기 설계에 적합하다. RANS가 예측한 리프트는 대개 실제 리프트의 몇 퍼센트 이내다.

비시크-흐름 방정식(Euler 또는 전위)

오일러 방정식은 점성, 열 전도 및 난류 효과가 없는 NS 방정식이다.^[105] 오일러 용액은 RANS 용액과 마찬가지로 에어포일을 둘러싼 점의 밀집 격자에서 정의된 속도 벡터, 압력, 밀도 및 온도로 구성된다. 오일러 방정식은 NS 방정식보다 간단하지만, 정확한 분석 용액에는 도움이 되지 않는다.

잠재적 흐름 이론을 통해 추가적인 단순화를 이용할 수 있는데, 이는 결정될 미지의 수를 줄이고, 일부 경우에는 아래에 기술한 바와 같이 분석적 해결이 가능하게 한다.

오일러 또는 전위 흐름 계산에서는 총 리프트를 최대 10–20% 놓칠 수 있는 스톨 아래의 공격 각도에 대해 에어포일 표면의 압력 분포를 대략 정확하게 예측한다. 스톨 위에서의 공격 각도에서 비실수적 계산은 스톨이 발생했다고 예측하지 못하며, 그 결과 리프트를 엄청나게 과대평가한다.

전위 흐름 이론에서 흐름은 비회전적인 것으로 가정한다. 즉, 작은 유체 소포는 순 회전율이 없다. 수학적으로 이것은 속도 벡터장의 컬이 0과 같은 모든 곳에 있다는 문장으로 표현된다. 비회전 흐름은 속도를 전위라고 하는 스칼라 함수의 구배로서 표현할 수 있는 편리한 특성을 가지고 있다. 이런 식으로 표현된 흐름을 전위 흐름이라고 한다.^{[106][107][108][109]}

전위 흐름 이론에서 흐름은 압축할 수 없는 것으로 가정한다. 비압축성 전위 흐름 이론은 잠재력에 대해 해결할 방정식(Laplace의 방정식)이 선형이라는 장점이 있어 다른 알려진 용액의 중첩에 의해 용액이 구성될 수 있다. 불압력-잠재-흐름 방정식은 복합 변수의 함수 이론에 기초한 방법인 정합성 매핑을 통해서도 풀 수 있다. 컴퓨터가 이용되기 전인 20세기 초, 순응 매핑을 사용하여 이상화된 공기포일 형태의 종류에 대한 압축 불가능한 전위-흐름 방정식에 대한 솔루션을 생성하여 리프팅 공기포일의 압력 분포에 대한 최초의 실제 이론적 예측을 제공하였다.

전위 방정식의 용액이 속도장만을 직접 결정한다. 압력장은 베르누이의 방정식을 통해 속도장으로부터 추론된다.

리프팅 흐름에 전위 흐름 이론을 적용하려면 특별한 처리와 추가적인 가정이 필요하다. 문제는 비실비실 흐름에서 에어포일 리프트는 에어포일 주위의 흐름의 순환을 요구하기 때문에 발생한다(아래 "순환 및 쿠타-주코스키 정리" 참조). 그러나 에어포일 주위의 영역 전체에 걸쳐 연속되는 단일 전위 함수는 제로 순환을 가진 흐름을 나타낼 수 없기 때문이다. 이 문제에 대한 해결책은 에어포일 표면의 어느 지점에서 무한 거리까지 분기 컷, 곡선 또는 라인을 도입하고 컷을 가로질러 전위값의 점프를 허용하는 것이다. 잠재적 점프는 잠재적 점프와 동일한 흐름의 순환을 유발하므로 0이 아닌 순환을 나타낼 수 있다. 그러나 전위점프는 전위 방정식이나 다른 경계조건에 의해 결정되지 않는 자유 매개변수로, 따라서 해법은 불확실하다. 순환의 모든 값과 리프트의 모든 값에 대해 잠재적 흐름 솔루션이 존재한다. 이러한 난연함을 해결하는 한 가지 방법은 쿠타 조건을 부과하는 것인데,^[110][111] 가능한 모든 해결책 중에서 물리적으로 타당한 해결책은 흐름이 후행 가장자리를 부드럽게 떠나는 것이다. 능률화 스케치는 유량이 후행 가장자리를 돌고 후행 가장자리의 앞쪽으로 상면을 떠나는 제로 리프트의 흐름 패턴을, 쿠타 조건에 따라 후행 가장자리에서 유량이 부드럽게 떠나는 플러스 리프트의 흐름 패턴을 각각 보여준다.

선형화된 전위 흐름

이것은 에어포일이 매우 얇고 공격 각도가 작다는 추가적인 가정을 가진 전위 흐름 이론이다.^[112] 선형화된 이론은 에어포일 압력 분포의 일반적인 특징과 그것이 에어포일 형태와 공격 각도에 의해 어떻게 영향을 받는지 예측하지만, 설계 작업에 충분히 정확하지는 않다. 2D 에어포일의 경우, 그러한 계산은 PC의 스프레드시트에서 1초 이내에 수행될 수 있다.

Circulation과 Kutta-Joukowski 정리

에어포일이 리프트를 생성할 때, 전체 속도장의 몇 가지 구성 요소는 에어포일 앞의 상향 흐름, 위의 가속 흐름, 아래의 감속 흐름, 뒤의 하향 흐름 등 공기 순환에 기여한다.

순환은 공기포일 주위의 비실비실 액체의 "회전" (또는 vorticity)의 총량으로 이해할 수 있다.

Kutta-Joukowski 정리는 2차원 에어포일의 단위 폭당 리프트를 흐름의 이 순환 요소에 관련시킨다.^{[85][113][114]} 에어포일이 정지 상태에서 움직임을 시작하고 출발 소용돌이가 형성되어 남으면서 에어포일 주위의 흐름이 발달함에 따라 에어포일 주위의 순환이 형성되는 것에 따르는 리프트 설명의 핵심 요소다.^{[115][116][117]} 그런 다음 리프트는 쿠타-주코프스키 정리로부터 유추된다. 이 설명은 대체로 수학적이며, 그 일반적인 진행은 물리적 인과관계가 아닌 논리적 추론에 근거한다.^[118]

쿠타-주코프스키 모델은 2차원 에어포일이 얼마나 많은 순환이나 리프트를 생산할지는 예측하지 못한다. Kutta-Joukowski를 사용하여 단위경간당 리프트를 계산하려면 순환에 대해 알려진 값이 필요하다. 특히 후미 정체점이 에어포일 후행 가장자리로 이동하여 비행 기간 동안 부착하는 쿠타 조건이 충족되면 정합 지도법을 통해 이론적으로 리프트를 계산할 수 있다.

기존 에어포일에 의해 발생하는 리프트는 설계와 전방 속도, 공격 각도 및 공기 밀도와 같은 비행 조건에 의해 결정된다. 리프트는 예를 들어 경계층 송풍 또는 송풍 플랩의 사용과 같이 인위적으로 순환을 증가시킴으로써 증가할 수 있다. Flettner 로터에서는 전체 에어포일이 원형이며, 순환을 만들기 위해 스판 축을 중심으로 회전한다.

3차원 흐름

3차원 날개 주위의 흐름은 특히 날개 끝과 관련된 상당한 추가적인 문제를 포함한다. 전형적인 델타 날개와 같이 가로 세로 비율이 낮은 날개의 경우, 2차원 이론은 좋지 않은 모델을 제공할 수 있고 3차원 흐름 효과가 지배적일 수 있다.^[119] 가로 세로 비율이 높은 날개의 경우에도 한정된 스팬과 관련된 3차원 효과는 끝에만 가까운 것이 아니라 전체 스팬에 영향을 미칠 수 있다.

날개 팁 및 스팬웨이즈 분포

날개 끝의 수직 압력 구배는 공기가 측면으로 흐르게 하고 날개 아래에서 밖으로 나온 다음 상부 표면 위로 위와 뒤로 흐르게 한다. 이렇게 하면 날개 끝의 압력 구배가 감소하므로 리프트도 감소한다. 리프트는 루트부터 팁까지 스팬웨이 방향으로 감소하는 경향이 있으며, 에어포일 섹션 주변의 압력 분포는 스팬웨이 방향으로 변화한다. 비행 방향에 수직인 평면의 압력 분포는 오른쪽 그림처럼 보이는 경향이 있다.^[120] 이 수평방향 변압 분포는 속도장과의 상호 작용에 의해 유지된다. 날개 아래의 흐름은 바깥쪽으로 가속되고, 팁의 흐름 바깥쪽은 위로 가속되며, 날개 위의 흐름은 안쪽 방향으로 가속되어 오른쪽에 표시된 흐름 패턴이 나타난다.^[121]

동일한 에어포일 형태와 단면 리프트를 가진 2차원 흐름에서보다 아래쪽으로 흐름이 전환되며, 2차원 흐름에 비해 동일한 리프트를 달성하려면 더 높은 단면 공격 각도가 필요하다.^[122] 날개는 2차원에 비해 전체 공기역학력 벡터가 약간 뒤로 기울어진 결과 프리스트림 흐름이 아래로 기울어진 것처럼 자체 제작의 다운드래프트로 효과적으로 비행하고 있다. 힘 벡터의 추가적인 후방 요소를 리프트 유도 드래그라고 한다.

날개 위와 아래 속도의 스팬와이드 성분 차이(아래 선외기 방향과 선외기 방향 사이)는 후행 에지에서 그리고 웨이크 다운스트림까지 지속된다. 흐름이 후행 가장자리를 떠난 후, 이 속도 차이는 보텍스 시트라고 불리는 상대적으로 얇은 전단 층에 걸쳐 발생한다.

말발굽 보텍스 시스템

날개를 떠나는 날개끝의 흐름이 끝 소용돌이를 만들어낸다. 주 소용돌이 시트가 후행 가장자리에서 하류로 통과할 때 바깥쪽 가장자리에서 롤업하여 팁 보티스와 합쳐진다. 날개끝 보트와 보텍스 시트가 결합하여 먹이를 주는 것을 보텍스 웨이크라고 한다.

후행 소용돌이 웨이크에 있는 vorticity 외에도 날개의 경계층에는 'bound vorticity'라고 불리는 vorticity가 있는데, 이것은 날개의 양쪽에서 오는 후행 시트를 말굽의 일반적인 형태로 소용돌이 시스템으로 연결한다. 소용돌이 체계의 편자 형태는 1907년 영국의 항공학의 선구자 란체스터에 의해 인정되었다.^[123]

결합성(bound vorticity)과 후행성(vorticity)의 분포를 고려할 때, Biot-Savart 법칙(벡터-미적분학 관계)을 사용하여 날개의 리프트에 의해 야기되는 필드 내 어느 곳에서든 속도 동요를 계산할 수 있다. 3차원 날개의 리프트 분포와 리프트 유도 항력에 대한 대략적인 이론은 날개의 말발굽 소용돌이 시스템에 적용된 그러한 분석에 기초한다.^[124][125] 이러한 이론에서, 결합 vorticity는 일반적으로 이상화되어 날개 내부의 캠버 표면에 상주하는 것으로 가정된다.

그러한 이론에서 속도는 vorticity에서 추론되기 때문에, 일부 저자들은 " 소용돌이에 의해 유도되는 속도"와 같은 용어를 사용하여 vorticity가 속도 동요의 원인임을 암시하는 상황을 설명한다.^[126] 그러나 이러한 방식으로 vorticity와 속도 사이의 기계적 인과관계를 탓하는 것은 물리학과 일치하지 않는다.^{[127][128][129]} 날개 주위의 흐름의 속도 동요는 사실 압력장에 의해 생성된다.^[130]

원야에서의 양력 표시

리프팅 흐름에서 통합된 힘/모멘텀

리프팅 에어포일 주위의 흐름은 흐름 영역의 모든 지점에서 그리고 흐름의 확장된 영역에 걸쳐 통합된 의미에서 운동량 보전에 관한 뉴턴의 두 번째 법칙을 충족시켜야 한다. 확장된 영역의 경우, 뉴턴의 두 번째 법칙은 제어 볼륨에 대한 모멘텀 정리 형태를 취하는데, 여기서 제어 볼륨은 분석을 위해 선택된 흐름의 어떤 영역이 될 수 있다. 모멘텀 정리에서는 제어 부피(표면 적분)의 경계에서 발휘되는 통합력이 제어 부피 내부를 통과하는 유체 구획의 모멘텀의 통합 시간 변화율(물질 파생율)과 동일하다고 기술하고 있다. 일정한 흐름의 경우, 이것은 경계를 통과하는 운동량의 흐름의 순 표면 적분 형태로 표현할 수 있다.^[131]

2D 에어포일 주위의 리프팅 흐름은 일반적으로 에어포일을 완전히 둘러싸는 제어 부피로 분석되므로 제어 부피의 내부 경계는 에어포일 표면으로, 유닛 스팬당 하방력${\displaystyle }$- ${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\$디스플레이 $스타일 -L'}$이 에어포일에 의해 액체에 가해진다. 바깥 경계는 보통 큰 원이나 큰 직사각형이다. 에어포일로부터 멀리 떨어진 이 외부 경계에서 속도와 압력은 균일한 흐름과 연관된 속도와 압력에 의해 잘 표현되며, 점성 응력은 무시할 수 있으므로 외부 경계 위로 통합되어야 하는 유일한 힘은 압력이다.^{[132][133][134]} 자유 흐름 속도는 수직 상승으로 수평으로 가정하여 수직 모멘텀이 관심의 구성요소가 되도록 한다.

자유공기 케이스(지상면 없음)의 경우, 유체에 대한 에어포일이$$ 가하는${\displaystyle }$힘 - $\$ {\$displaystyle$-L'은 오른쪽 다이어그램에서와 같이 외부 경계의 모양에 따라 비례하는 비율로 부분적으로 모멘텀 플럭스 및 외부 경계에서의 압력 차이로 나타난다. 높이보다 훨씬 긴 평평한 수평 직사각형의 경우 앞뒤를 통과하는 수직 운동량의 유속이 무시할 수 있으며, 리프트는 전적으로 상하의 통합 압력 차이에 의해 설명된다.^[132] 사각형이나 원의 경우, 모멘텀 플럭스와 압력 차이가 리프트 각각 절반을 차지한다.^{[132][133][134]} 넓이보다 훨씬 높은 수직 직사각형의 경우 위와 아래쪽의 불균형한 압력력은 무시할 수 있으며, 리프트는 전적으로 모멘텀 플럭스에 의해 설명되며, 전방으로 제어 볼륨에 진입하는 상향 모멘텀 플럭스는 리프트의 반을 설명하며, 제어에서 빠져나가는 하향 모멘텀 플럭스는 전적으로 모멘텀 플럭스에 의해 설명된다.나는 나머지 절반의 뒷부분을 볼륨으로 처리한다.^[132]

위에서 설명한 모든 제어 체적 분석 결과는 위에서 설명한 쿠타-주코프스키의 정리와 일치한다. 장신 사각형과 원 컨트롤 볼륨은 모두 정리의 파생에 사용되어 왔다.^[133][134]

비행기 아래 지면에서 과도한 압력에 의해 리프트가 반응함

위의 "에어포일 주위의 더 넓은 흐름"에서 설명한 바와 같이 에어포일은 주변 공기에 압력장을 생성한다. 이 장과 관련된 압력 차이는 점차 소멸되어, 먼 거리에서는 매우 작아지지만, 완전히 사라지지는 않는다. 비행기 아래에서는 압력장이 지면에 도달하는 양압 교란으로 지속되어 오른쪽과 같이 지면에 약간 높은 압력보다 높은 압력 패턴을 형성하고 있다.^[135] 비록 기압차가 비행기보다 훨씬 아래에 매우 작지만, 그것들은 넓은 지역에 퍼져 있고 상당한 힘을 더한다. 안정적이고 평탄한 비행의 경우, 압력 차이로 인한 통합력은 비행기의 총 공기역학적 양력과 비행기의 무게와 동일하다. 뉴턴의 제3법칙에 따르면, 공기에 의해 지면에 가해지는 이 압력력은 지면에 의해 공기에 가해지는 등반대의 상승력과 일치하며, 이는 비행기에 의해 공기에 가해지는 모든 하방력을 상쇄한다. 따라서 전체적인 대기에 작용하는 리프트에 의한 순력은 0이며, 따라서 현대 공기역학 개발 초기에 란체스터가 지적한 바와 같이 대기에 수직 운동량이 통합적으로 축적되지 않는다.^[136]

참고 항목

• 드래그 계수
• 흐름 분리
• 유체 역학
• 포일(유체 역학)
• 쿠스너 효과
• 리프트-드래그 비율
• 리프팅 라인 이론
• 스포일러(자동차)

각주

참조

추가 읽기

외부 링크

• 리프트에 대한 다양한 설명 사이의 명백한 "충돌"에 대한 논의
• 항공우주국(NASA) 튜토리얼, 애니메이션 포함, 리프트 설명
• NASA FileSim II 1.5 베타. 리프트 시뮬레이터
• 에어포일 주위의 유체 흐름 애니메이션을 이용한 리프트 설명
• 압력에 초점을 맞춘 날개가 양력을 생성하는 이유와 방법에 대한 치료
• 비행물리학 – 검토. 교수별 온라인 논문 클라우스 웰트너 박사
• 날개는 어떻게 작동하는가? 홀거 바빈스키
• 베르누이 또는 뉴턴: 리프트에 대해 누가 옳은가? 플레인 앤 파일럿 매거진
• 1분 물리학 날개는 실제로 어떻게 작동하는가? (유튜브 비디오)
• 날개가 실제로 어떻게 작동하는가, 케임브리지 대학교 홀거 바빈스키("일분 물리학 어떻게 날개가 실제로 작동하는가?") 유튜브 동영상)
• 정상에서 해저까지 – 롤프 스티네거가 고도와 깊이의 함수로써 들어올린 중량
• Joukowski Transformation WebApp
• 미시간대 항공우주공학과 부교수인 크리즈토프 피드코프스키의 '플레인스 플라이 유투브(Flaces flying YouTube