에어포일

에어포일(미국식 영어) 또는 에어로포일(영국식 영어)은 날개, 돛 또는 프로펠러, 회전자 또는 터빈의 날개와 같은 기체를 통한 움직임이 상당한 양력을 발생시킬 수 있는 물체의 단면 형상입니다.

유체 속을 이동하는 고체체는 공기역학적 힘을 생성합니다.상대 자유류 속도에 수직인 이 힘의 성분을 리프트라고 합니다.상대적인 자유류 속도에 평행한 성분을 드래그라고 합니다.에어포일은 ^[1]드래그보다 훨씬 더 많은 양력을 발생시킬 수 있는 유선형 형태입니다.아음속 비행용 에어포일은 일반적으로 둥근 선단을 가지고 있는 반면 초음속 비행용 에어포일은 날카로운 선단을 가지고 더 얇아지는 경향이 있습니다.모두 날카로운 뒷부분을 가지고 있다.작동 유체와 물로 설계된 유사한 기능을 가진 박을 수중익이라고 합니다.

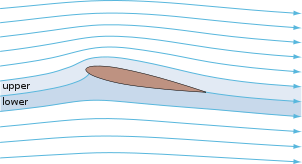
에어포일의 양력은 주로 공격 각도의 결과입니다.적절한 각도로 방향을 잡을 때, 에어포일은 마주 오는 공기를 편향시켜(고정익 항공기의 경우, 하향력), 결과적으로 에어포일에 반대 방향으로 힘을 가한다.이 힘은 공기역학적 힘이라고 하며 양력과 드래그라는 두 가지 요소로 분해할 수 있습니다.대부분의 호일 모양은 양력을 발생시키기 위해 양의 공격 각도가 필요하지만, 캠버형 에어포일은 0의 공격 각도로 양력을 발생시킬 수 있습니다.에어포일 근처에서 공기가 "회전"하면 곡선 유선형 구조가 형성되어 한쪽은 압력이 낮아지고 다른 한쪽은 압력이 높아집니다.이 압력 차이는 베르누이의 원리에 따라 속도 차이를 동반하기 때문에 에어포일 주위의 흐름장은 하부 표면보다 상부 표면에서 더 높은 평균 속도를 가집니다.일부 상황(예: 비점상 전위 흐름)에서 리프트 힘은 순환의 개념과 쿠타-주코프스키 ^[a][2][3][b]정리를 사용하여 압력을 계산하지 않고 평균 상단/하단 속도 차이에 직접 관련될 수 있다.

개요

헬리콥터 로터 블레이드뿐만 아니라 고정익 항공기의 날개와 안정기는 날개 모양의 단면으로 제작된다.에어포일은 또한 프로펠러, 팬, 압축기, 터빈에서도 발견된다.돛은 또한 날개 모양이고, 센터보드, 방향타, 용골과 같은 돛단배의 수중 표면은 단면이 비슷하고 날개 모양과 같은 원리로 작동한다.수영과 날으는 생물들, 그리고 심지어 많은 식물과 세실 유기체들도 날개와 수중 날개들을 사용합니다: 흔한 예로는 새의 날개, 물고기의 몸, 모래 달러 모양입니다.날개 모양의 날개는 자동차나 다른 자동차에 다운포스를 만들어 트랙션을 향상시킬 수 있습니다.

바람이 평판, 건물 또는 다리의 갑판과 같은 물체에 의해 방해되면 물체는 드래그와 바람에 수직인 공기역학적 힘을 경험하게 됩니다.이는 객체가 에어포일로 적합하다는 것을 의미하지 않습니다.에어포일은 매우 효율적인 리프팅 형태이며, 같은 면적의 비슷한 크기의 평판보다 더 많은 양력을 발생시킬 수 있으며, 훨씬 적은 항력으로 양력을 발생시킬 수 있습니다.에어포일은 항공기, 프로펠러, 로터 블레이드, 풍력 터빈 및 기타 항공 공학의 용도에 사용됩니다.

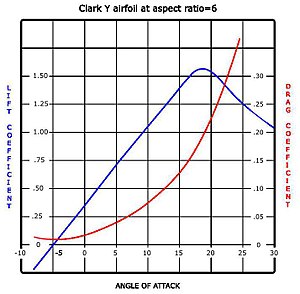
풍동 테스트에서 얻은 리프트 및 드래그 곡선은 오른쪽에 표시되어 있습니다.곡선은 양의 캠버를 가진 에어포일을 나타내므로 일부 리프트는 0의 공격 각도로 생성됩니다.공격 각도가 증가하면 리프트 곡선의 기울기라고 하는 대략적인 선형 관계에서 리프트가 증가합니다.약 18도에서 이 날개가 멈춘다. 그리고 그 너머로 양력이 빠르게 떨어진다.리프트의 하락은 상부 표면 경계층의 작용으로 설명할 수 있으며, 상부 표면 경계층은 스톨 각도와 스톨 각도에서 상부 표면 위로 분리되고 크게 두꺼워집니다.두꺼워진 경계층의 변위 두께는 에어포일의 유효 형상을 변화시키며, 특히 에어포일의 유효 캠버를 감소시켜 순환과 양력을 감소시키도록 전체 흐름장을 변경합니다.또한 경계층이 두꺼우면 압력 항력이 크게 증가하여 전체 항력이 정지점 근처와 스톨점을 지나 급격히 증가합니다.

에어포일 디자인은 공기역학의 주요 측면입니다.다양한 에어포일은 다양한 비행 방식을 제공한다.비대칭 에어포일은 공격 각도가 0인 상태에서 양력을 발생시킬 수 있는 반면, 대칭 에어포일은 곡예 비행기에서처럼 빈번한 역비행에 더 적합할 수 있습니다.날개 끝과 날개 끝 부근에서 대칭 날개 모양을 사용하여 공격 각도의 범위를 늘려 스핀-스톨을 방지할 수 있습니다.따라서 경계층을 분리하지 않고 넓은 범위의 각도를 사용할 수 있습니다.아음속 에어포일은 끝이 둥글고 공격 각도에 민감하지 않습니다.단, 단면이 엄밀하게 원형인 것은 아닙니다. 단, 테두리 층이 분리될 가능성을 최소화하기 위해 날개가 최대 두께에 도달하기 전에 곡률 반경을 증가시킵니다.이렇게 하면 날개가 길어지고 최대 두께의 점이 앞쪽 가장자리에서 뒤로 이동합니다.

초음속 에어포일은 훨씬 더 각진 모양을 하고 있고 공격 각도에 매우 민감한 날카로운 앞부분을 가질 수 있습니다.초임계 에어포일은 초음속의 흐름을 아음속으로 천천히 충격시킬 수 있는 많은 길이를 가지기 위해 가장 앞 가장자리에 가까운 최대 두께를 가지고 있습니다.일반적으로 이러한 트랜조닉 에어포일과 초음속 에어포일은 항력 차이를 줄이기 위해 캠버가 낮습니다.최신 항공기 날개는 날개 스팬을 따라 서로 다른 날개 날개 부분을 가질 수 있으며, 각 날개 부분의 조건에 최적화되어 있다.

거의 모든 항공기의 에어포일에 이동식 하이 리프트 장치, 플랩 및 때때로 슬랫이 장착됩니다.테일링 에지 플랩은 에일러론과 유사하게 작동하지만, 에일러론과 달리 사용하지 않을 경우 부분적으로 날개로 후퇴할 수 있습니다.

층류 윙은 중앙 캠버 라인의 최대 두께를 가집니다.Navier 분석–선형 시스템의 스토크스 방정식은 흐름을 따라 부압 구배가 속도를 감소시키는 것과 같은 효과가 있음을 보여줍니다.따라서 최대 캠버가 중앙에 있을 때 더 높은 순항 속도에서 더 많은 비율의 윙에 걸쳐 층류 유량을 유지할 수 있습니다.그러나 일부 표면 오염은 층류 흐름을 방해하여 난류를 일으킨다.예를 들어, 날개에 비가 내리면 흐름이 거칠어집니다.특정 조건에서는 날개의 곤충 파편이 층류 중 작은 영역의 손실을 야기할 수 있습니다.^[4]1970년대와 1980년대 NASA의 연구 이전에 항공기 설계 커뮤니티는 제2차 세계대전 당시의 응용 시도로부터 층류 날개 설계가 일반적인 제조 공차와 표면 결함을 사용하여 실용적이지 않다는 것을 이해했다.이러한 믿음은 복합 재료(예: Franz Wortmann 교수가 섬유 강화 플라스틱으로 만든 날개에 사용하기 위해 개발한 층류 에어포일)를 사용하여 새로운 제조 방법이 개발된 후 바뀌었다.가공된 금속 방식도 도입되었다.NASA의 1980년대 연구는 층류 날개 설계의 실용성과 유용성을 밝혀냈고 아음속 일반 항공기에서부터 트랜스오닉 대형 수송기에 이르기까지 현대의 실용적인 항공기 표면에 층류 설계를 적용할 수 있는 길을 열었다.^[5]

에어포일을 정의하는 방식이 고안되었습니다.예를 들어 NACA 시스템이 있습니다.다양한 에어포일 생성 시스템도 사용됩니다.범용 에어포일의 예로서 광범위한 응용 프로그램을 찾아 NACA 시스템을 사전 연월일화하는 것이 Clark-Y입니다.오늘날, 에어포일은 컴퓨터 프로그램을 사용하여 특정 기능을 위해 설계될 수 있다.

에어포일 용어

에어포일과 관련된 다양한 용어가 아래에 정의되어 있습니다.^[6]

• 흡입 표면(상부 표면)은 일반적으로 더 높은 속도와 더 낮은 정적 압력과 관련이 있습니다.
• 압력 표면(하부 표면)은 흡입 표면보다 정적 압력이 상대적으로 높습니다.이 두 표면 사이의 압력 구배는 주어진 에어포일에 대해 발생하는 리프트력에 기여한다.

에어포일의 형상은 다양한 용어로 설명됩니다.

• 선행 에지는 최대 곡률(최소 반지름)^[7]을 가진 에어포일 전면의 지점입니다.
• 후행 가장자리는 에어포일 후면의 최대 곡률 지점과 유사하게 정의됩니다.
• 코드 라인은 선행 에지와 후행 에지를 연결하는 직선입니다.코드 길이 또는 간단히 말하면 코드 $c\backslash$$displaystyle$c는 코드 라인의 길이입니다.그것은 날개 부분의 기준 치수입니다.

에어포일의 모양은 다음 기하학적 매개변수를 사용하여 정의됩니다.

• 평균 캠버 라인 또는 평균 라인은 상부 표면과 하부 표면 사이의 중간 지점 궤적입니다.모양은 화음을 따라 두께 분포에 따라 달라집니다.
• 날개의 두께는 화음에 따라 다르다.다음 두 가지 방법 중 하나로 측정할 수 있습니다.
  • 캠버 ^[8][9]라인에 수직으로 측정된 두께입니다.이를 '미국 협약'^[8]이라고 부르기도 한다.
  • 코드 ^[10]라인에 수직으로 측정된 두께입니다.이것은 때때로 "영국 협약"으로 묘사된다.

에어포일의 형태를 설명하는 몇 가지 중요한 매개변수는 캠버와 두께입니다.예를 들어 NACA 2415와 같은 NACA 4자리 시리즈의 에어포일(2~4~15로 읽음)은 캠버가 0.02 코드인 에어포일을 0.40 코드, 최대 두께 0.15 코드인 에어포일을 나타냅니다.

마지막으로, 유체 속을 이동할 때 에어포일의 동작을 설명하는 데 사용되는 중요한 개념은 다음과 같습니다.

• 공기역학적 중심, 즉 피칭 모멘트가 리프트 계수 및 공격 각도와 무관한 현측 위치입니다.
• 피칭 모멘트가 순간적으로 0이 되는 현상의 위치인 압력의 중심.캠버 날개에서 압력의 중심은 공격각도와 양력계수의 변화에 따라 움직이기 때문에 고정된 위치가 아니다.

얇은 날개 이론

얇은 날개 이론은 압축할 수 없는, 비점상적인 흐름을 위해 들어올릴 수 있는 공격 각도를 관련짓는 단순한 날개 이론입니다.그것은 독일 수학자 막스 멍크에 의해 고안되었고 1920년대에 영국의 공기역학자인 헤르만 글라우트와 다른^[11] 사람들에 의해 더욱 정교해졌다.이 이론은 날개 주변의 흐름을 얇은 날개 주변의 2차원 흐름으로 이상화한다.두께가 0이고 날개 폭이 무한인 에어포일을 다루는 것으로 상상할 수 있습니다.

얇은 날개 이론은 2차원 불시체 ^[12][13]흐름에서 날개 모양의 다음과 같은 중요한 특성에 대한 건전한 이론적 근거를 제공했기 때문에 그 당시에 특히 두드러졌습니다.

1. 대칭 날개에서, 압력의 중심과 공기역학적 중심은 일치하며, 앞 가장자리 뒤에 정확히 현의 1/4이 놓여있다.
2. 캠버형 날개에서 공기역학적 중심은 정확히 전방 가장자리 뒤에 현의 1/4이 있지만, 압력 중심 위치는 공격 각도가 변화할 때 이동한다.
3. 공격 라인 각도에 대한 리프트 계수의 기울기는 라디안당 $(\displaystyle$ 2\$pi \!)$ $단위$입니다.

(3)의 결과로, 무한 날개 폭의 대칭 날개의 단면 리프트 계수는 다음과 같다.

$\displaystyle \c_{l}=2\pi \alpha }$

${\displaystyle c_{}}$ l${\displaystyle {}_{}}${ $displaystyle c$_ { $l$} \ ! }는$$ 섹션 리프트 계수입니다.

${\displaystyle }$α$(\$는 라디안 단위의 공격각으로 코드 라인에 대해 측정됩니다.

(상기 표현은 캠버형 에어포일에도 적용할 수 $있습니다{\displaystyle }$.여기서$$α$(\displaystyle$ \alpha $\!)$는 코드 라인이 아닌 제로 리프트 라인에 대해 측정된 공격 각도입니다.)

또한 (3)의 결과로 무한 날개폭의 캠버 에어포일의 단면 리프트 계수는 다음과 같다.

${\displaystyle \c_{l}=c_{l_{0}}+2\pi \alpha }$

${\displaystyle {여기}_{}}$서 c l $(\$은 공격각이 0일 때의 단면 리프트 계수입니다.

얇은 에어포일이론은 에어포일의 스톨을 설명하지 않습니다.일반 에어포일의 ^[14]경우 보통 10°에서 15° 사이의 공격 각도에서 발생합니다.그러나 2000년대 중반 월러스 모리스 2세가 박사학위 ^[15]논문에서 첨단 노점의 시작을 예측하는 이론을 제시했다.Morris의 후속 개선사항에는 최첨단 스톨 ^[16][17]현상에 대한 이론적 지식의 현재 상태에 대한 세부사항이 포함되어 있습니다.Morris 이론은 내부 흐름에 ^[18]대한 용액에서 전역 분리대가 예측되는 조건으로 첨단 스톨 발생에 대한 임계 공격 각도를 예측한다.모리스의 이론은 얇은 날개 주변의 아음속 흐름이 날개 현의 대부분 주변 외부 영역과 점근적으로 서로 일치하는 코 주변의 내부 영역으로 설명될 수 있다는 것을 보여줍니다.외부 영역의 흐름이 고전적인 얇은 날개 이론에 의해 지배되기 때문에, 모리스의 방정식은 얇은 날개 이론의 많은 구성 요소를 보여줍니다.

얇은 날개 이론의 도출

이 섹션은 어떠한 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션의 개선에 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.(2018년 11월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

에어포일은 얇은 리프팅 평균선(캠버 라인)으로 모델링됩니다.평균선 y(x)는 선 s를 따라 소용돌이${\displaystyle }\theta {\displaystyle }$ ( ${\displaystyle s}$ $)\style \gamma(s)$의 분포를 생성하는 것으로 간주됩니다.Kutta 조건에 따라 후연에서 소용돌이는 0이 됩니다.에어포일이 얇기 때문에 s 대신 x(차드 위치)를 사용할 수 있으며 모든 각도를 작게 근사할 수 있습니다.

Biot-Savart의 법칙에 따라 이 소용돌이는 ($)$ {$displaystyle w($x${\displaystyle )\}}$의 $흐름장$을 생성합니다.

${\displaystyle w(x)=syslogfrac {1}{(2\pi)}}\int _{0}^{c}{\frac {\frac (x')}}}},{(x-x')}},frac'}$

$({displaystyle$x})는 유도속도가 발생하는 위치, x$({$ x$')$는 속도를 생성하는 소용돌이 요소의 위치, $({displaystyle$c})는$$ 에어포일의 코드 길이입니다.

에어포일의 곡면에 수직인 흐름이 $없으므로{\displaystyle }$ w${\displaystyle }$(${\displaystyle }$x$$) {$디스플레이 스타일$$$w$(x)}$는 플레이트에 국소적으로 정상적인 메인 $플로우{\displaystyle }$ V ${\displaystyle$ V$\}$의 구성 요소로부터 균형을 잡습니다. 메인 플로우는 국소적으로 플레이트에 대해${\displaystyle }$α - ${\displaystyle dy}$ / ${\displaystyle d}$x {\$display style \alpha$ - dx$\}$ $각도$만큼 기울어집니다.즉, 다음과 같습니다.

$(\displaystyle V\;(\alpha - dy / pi )=w(x)=snot frac {1}{0}^{c}{\frac {\frac (x')}}}}}}},frac ',frac'입니다.}$

$이{\displaystyle }$ 적분방정식은 x를 다음과 같이 치환한 후 ${\displaystyle (}$ (${\displaystyle x}$) \ $displaystyle$\$gamma$($$x )에 대해 풀 수 있습니다.

${\displaystyle x=c\cdot {1-\cos(\theta)}{2}}$

A ${\displaystyle n}$ sin ${\displaystyle (}$ ( $n$($$) {${\displaystyle \mathrm{displaystyle}}$ $A$${\displaystyle {\_\mathrm{}}_{}}${ $n$$$} \$sin$ ($n$ \ $theta$) } 에서의 푸리에 급수로서, A $0{\displaystyle {}_{}}$($1$+ cos${\displaystyle (}$ ) / ${\displaystyle \sin (}$ ( ${\displaystyle )}$) {$displaystyle$ A_{0} ( 1 + cos ( \ theta ) / sin ( \ ta$)$ } } ) / $sin$ ( \ sin ) } ) } ) 。

그것은

$(\displaystyle\frac(\theta){(2V)}}=A_{0}{\frac {(1+\cos(\theta)}}, {\sin(\theta)}}, +\sum A_{n}\sin(n\theta)},$

(이러한 항을 Glauert 적분이라고 합니다).

계수는 다음과 같이 지정됩니다.

${\displaystyle A_{0}=\alpha -{\frac {1}{\pi }}\int _{0}^{\pi }\leftflac {dy}}\right)d\theta }$

그리고.

${\displaystyle A_{n}=flac {2}{\pi }}\int _{0}^{\pi }\leftflac {dy}}\right)\cos(n\theta)\;d\theta.}$

Kutta-Joukowski 정리에 따르면, 총 리프트력 F는 다음과 비례한다.

$\displaystyle \rho V\int _{0}^{c}\gamma(x),dx}$

그리고 그것은 M의 최첨단에 대한 순간이다.

$\displaystyle \rho V\int _{0}^{c}x\;\gamma (x),dx.}$

계산된 리프트 계수는 다음과 같이 푸리에 급수의 처음 두 항에만 의존합니다.

${\displaystyle C_{L}=2\pi (A_{0}+A_{1}/2).}$

선두에 관한 M의 모멘트는 ${\displaystyle {A\mathrm{}}_{}}$ 0${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ $({$ $및$ ${\displaystyle {A\mathrm{}}_{}}$ 2$({$에만 의존합니다.

${\displaystyle C_{M}=-0.5\pi(A_{0}+A_{1}-A_{2}/2).}$

따라서 1/4 화음점에 대한 모멘트는 다음과 같습니다.

$({displaystyle C_{M}(1/4c)=-\pi/4(A_{1}-A_{2}).}$

이로부터 압력의 중심이 '쿼터-코드' 지점 0.25 c의 후방에 오도록 한다.

$(\displaystyle \Delta x/c=\pi /4((A_{1}-A_{2})/C_{L}).}$

공기역학적 중심인 AC는 1/4 좌표 지점에 있습니다.AC는 상승 계수의 변화에 따라 피칭 모멘트 M†가 변화하지 않는 곳이다.

$(\displaystyle {\frac (C_{M')} {\partial (C_{L})} = 0 . }$

「 」를 참조해 주세요.

• 순환 제어 날개
• 수중익
• 클라인-포글먼 날개
• 퀴스너 효과
• 파라포일

레퍼런스

메모들

인용문

원천

추가 정보

• 알리 캄란페이, 알리레자 메흐라바디다양한 공격각도에서 NACA 에어포일 0012의 수치해석 및 공기역학 계수 취득메카트로닉스 및 자동화 저널.2019; 6(3): 8~16p.

외부 링크

• UIUC 에어포일 좌표 데이터베이스
• 에어포일 및 하이드로포일 레퍼런스 어플리케이션
• 미 항공우주국(NASA)의 날개 모양 시뮬레이터
• 에어포일 플레이그라운드 - 인터랙티브 웹앱
• 데스크탑에로
• 시드니 대학교, 학생들을 위한 공기역학^{[영구 데드링크]}

• 날개 전체의 공기 흐름(캠브리지 대학)

• https://engineeringjournals.stmjournals.in/index.php/JoMA/article/view/3639