내부반영합계

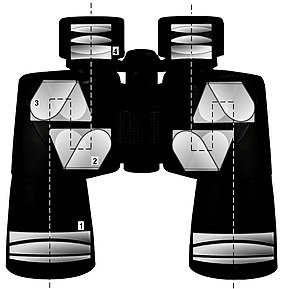
TIR(Total Internal Reflection, TIR)은 한 매체에서 다른 매체(예: 물에서 공기로)로 인터페이스(경계)에 도달하는 파동이 두 번째("외부") 매체로 굴절되지 않고 첫 번째("내부") 매체로 완전히 반사되는 광학적 현상이다.두 번째 매체가 첫 번째 매체에 비해 파속(굴절률 낮음)이 높고, 파동이 인터페이스에서 충분히 비스듬히 발생했을 때 발생한다.예를 들어, 일반적인 어항의 물대공 표면은 아래에서 비스듬히 볼 때, 밝기를 잃지 않는 거울처럼 수중 장면을 반영한다(그림 1).

TIR은 빛과 전자파와 같은 전자파뿐만 아니라 음파와 수파를 포함한 다른 종류의 파동에서도 발생한다.파동이 좁은 빔을 형성할 수 있는 경우(그림 2), 반사는 파동이 아닌 "선"의 관점에서 설명되는 경향이 있다. 공기, 물 또는 유리와 같이 방향과 독립적인 성질을 가진 매체에서 "선"은 관련 파형에 수직이다.

굴절은 일반적으로 부분반사를 동반한다.파동이 낮은 전파속도의 매체(높은 굴절률)에서 높은 속도의 매체(예: 물에서 공기로)로 굴절될 때 굴절각(출발 광선과 표면 정상 사이)은 입사각(입선 광선과 정상 사이)보다 크다.발생 각도가 임계 각도라고 불리는 특정 임계값에 가까워질 때 굴절 각도는 90°에 접근하며, 굴절된 광선이 경계 표면과 평행하게 된다.입사각이 임계각 이상으로 증가함에 따라 굴절조건은 더 이상 충족될 수 없으므로 굴절선이 없고 부분반사가 총체적으로 된다.가시광선의 경우 임계각은 물에서 공기로의 발생에 대해 약 49°이고, 일반 유리에서 공기로의 발생에 대해서는 약 42°이다.

TIR의 메커니즘에 대한 세부사항은 더욱 미묘한 현상을 야기한다.총반사는, 정의상, 두 매체 사이의 인터페이스에 걸친 전력의 지속적인 흐름을 수반하지 않지만, 외부 매체는 인터페이스로부터 거리에 따라 기하급수적으로 떨어져 나가는 진폭으로 인터페이스를 따라 이동하는 소위 전파파를 전달한다.외부 매체가 무손실(완벽하게 투명), 연속성 및 무한 범위인 경우 "총" 반영은 실제로 총합이지만, 방출파가 손실성 외부 매체("감쇠된 총 반사율")에 의해 흡수되거나 외부 매체의 외부 경계 또는 임베드 오브젝트에 의해 전용되는 경우 총보다 현저하게 적을 수 있다.이 매체의 에드("파쇄" TIR)투명 매체 사이의 부분반사와는 달리, 전체 내부반사에는 비종속적인 위상변동(0도 또는 180°만이 아님)이 수반된다.각 양극화 요소(발생 평면에 평행 또는 평행)에 대해, 그리고 변화는 발생 각도에 따라 달라진다.1823년 아우구스틴-장 프레스넬의 이러한 효과에 대한 설명은 빛의 파동 이론에 찬성하는 증거에 추가되었다.

위상변동은 프레넬의 발명품인 프레스넬 롬이 양극화를 수정하기 위해 활용한다.전체 내부 반사 효율은 광섬유(통신 케이블 및 영상 형성 섬유스코프에서 사용)와 단안경 및 쌍안경에 대한 이미지 보정 포로/지붕 프리즘과 같은 반사 프리즘에 의해 활용된다.

광학 설명

(예를 들어)초단파^[1], 음파 등 사선이 발생한다고 할 수 있는 어떤 종류의 파동에서도 총체적 내부반사가 일어날 수 있지만,^[2] 광파의 경우 가장 친숙하다.

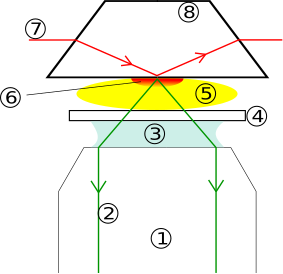
빛의 총체적 내부반사는 일반 유리나 아크릴 유리의 반원자-실린드 블록을 사용하여 시연할 수 있다.그림 3에서, "레이 박스"는 방사상으로 안쪽으로 좁은 광선("레이")을 투사한다.유리의 반원형 단면은 유입되는 광선이 공기/유리 표면의 곡선 부분에 수직으로 유지되도록 하며, 따라서 평탄한 부분과의 각도는 다르지만 평탄한 부분을 향해 직선으로 계속된다.

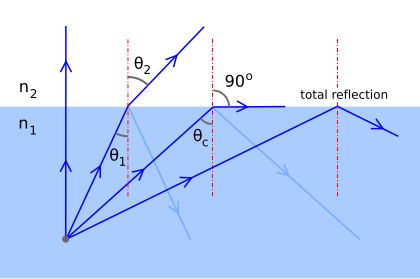
광선이 평면 유리 대 공기 인터페이스를 만나는 경우, 광선과 인터페이스에 대한 정상(수직) 사이의 각도를 발생 각도라고 한다.^[3]이 각도가 충분히 작을 경우, 광선은 부분적으로 반사되지만 대부분 전송되며, 전송된 부분은 정상으로부터 굴절되어 굴절각(굴절된 광선과 정상 사이의 간격)이 발생각보다 커진다.잠시, 발생각 θ과_i 굴절각 θ_t(t가 전송되는 경우, r을 반사되도록 예약)이라고 부르자.θ_ic(또는 때때로 sometimes_cr)로 나타내는 특정 "임계각"에 θ이 증가하여 접근함에 따라 굴절각은 90°(즉, 굴절된 광선은 접점에 접하는 접선에 접근함)에 접근하며, 굴절된 광선은 반사된 광선이 더 밝아지는 동안 더욱 희미해진다.^[4]θ이_i θ_c 이상으로 증가함에 따라 굴절된 광선은 사라지고 반사된 광선만 남게 되어 입사 광선의 모든 에너지가 반사된다. 이것이 총내반사(TIR)이다.요약하면:

• θ_i < θ_c, 입사 광선이 분할되어 부분적으로 반사되고 부분적으로 굴절되는 경우
• θ_i > θ이면_c 입사광은 총체적 내부반사(TIR)를 겪으며, 어느 것도 전송되지 않는다.

임계각

임계 각도는 전체 반사를 산출하는 가장 작은 발생 각도 또는 동등하게 굴절된 광선이 존재하는 가장 큰 각이다.^[5]단일 굴절률 n을₁ 가진 "내부" 매체에서 단일 굴절률 n을₂ 가진 "외부" 매체까지 발생하는 광파의 경우 임계 각도는 $\theta {\displaystyle {}_{}}$ ${\displaystyle c_{}}$= ${\displaystyle \arcsin }$ ${\displaystyle }$ ${\displaystyle ({}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$/ ${\displaystyle n{}_{}}$ ${\displaystyle {1\mathrm{}}_{}),}$ ${\displaystyle \theta _{\text{\c}\!$$}}=\arcsin(n_{2}/n_{1}\}).$ n₂ ≤ n이면₁ 정의된다$$. 다른 파형의 경우 굴절률보다는 전파속도 측면에서 생각하는 것이 편리하다.속도 측면에서 임계 각도에 대한 설명은 보다 일반적이며 따라서 먼저 논의될 것이다.

파전선이 한 매체에서 다른 매체로 굴절될 때 파전선의 입사(인입)과 굴절(아웃바운드) 부분은 굴절 표면(인터페이스)의 공통 선에서 만난다.L로 표시된 이 선은 표면에서 u 속도에서 움직이게 하고,^[6][7] u는 L에서 정상으로 측정한다(그림 4).입사 및 굴절파프론트는 정상 속도 $v{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ v${\$} 및$$ $v{\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}${\$displaystyle v_{2}}($존중하게)로 전파되도록 하고, 인터페이스로 이음각 θ₁ 및 θ₂(존중하게)을 만들도록 한다.기하학에서 $v{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$}는 입사파에 정상적인 방향으로 u의 구성 요소로서$$, $v{\displaystyle {}_{}}$ ${\displaystyle 1_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle \sin }$sin ${\displaystyle {1\mathrm{}}_{}}$.${\displaystyle v_{1\!$$}}=u\sin \theta _{1}\,.}$ 이와$$ ${\displaystyle {비슷하게\mathrm{}}_{}}$ v${\displaystyle {}_{}}$2 = ${\displaystyle u}$ ${\displaystyle \sin }$ θ${\displaystyle {}_{}{\theta \mathrm{}}_{}}$ 2.$${\$displaystyle v_{2}=u\sin \theta _{2}\,}$ 1/u에 대한 각 방정식을 풀고$$ 결과를 동일시하면서 파동에 대한 굴절의 일반 법칙을 얻는다.

${\displaystyle {\frac {\sin \theta _{1}{1}}={\frac {\sin _{2}}:{v_{2}}:}\,}$

(1)

그러나 두 평면의 이음각은 또한 평면 사이의 각이다.따라서 θ은₁ 입사파전선에 대한 정상과 인터페이스에 대한 정상 사이의 각도인 반면, θ은₂ 굴절파전선에 대한 정상과 인터페이스에 대한 정상 사이의 각도인 반면, Eq. (1)은 이러한 각도의 사인(sine)이 각각의 속도와 동일한 비율에 있음을 알려준다.^[8]

이 결과는 「스넬의 법칙」의 형태를 띠고 있는데, 아직 속도 비율이 일정하다고 말하지 않았거나, 발생 각도와 굴절각(위 θ_i, θ_t)을 확인했다고는 하지₁ 않았다(위₂ θ, θ라고 한다).만약 이제 우리는 미디어의 속성이 등방성(방향의 독립)것 같아 하지만, 두가지의 더욱 심오한 결론:첫째, 두 속도, 이 때문에 그들의 비율, 방향을을 광선으로 둘째,wave-normal 방향 일치하다는 독립적인 그래서를 따르는 것이 입사의 각도와θ2θ1 일치한다. a위에서 정의한 바와 같이 굴절.^{[Note 1]}

분명히 굴절 각도는 90°를 초과할 수 없다.제한 사례의 경우, Eq. (1)에₂ = = 90° 및₁ = = θ를_c 넣고 임계 각도에 대해 해결한다.

${\displaystyle \theta _{\text{c}=\arcsin(v_{1}/v_{2})\,}$

(2)

이 결과를 도출할 때, 발생각과 굴절각으로 with과₁ θ을₂ 식별하기 위해 등방성 매체의 가정을 유지한다.^{[Note 3]}

전자파의 경우, 특히 빛의 경우, 위의 결과를 굴절률의 관점에서 표현하는 것이 관례다.정상 속도 $v{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$}를 가진 매체의 굴절 ${\displaystyle {지수는}_{}}$n ${\displaystyle 1}$= c / ${\displaystyle v{}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle n_{1\!$로 정의된다$$.$}}=c/v_{1}\}$ 여기서$$ c는 진공에서 빛의 속도다.^[9] 따라서 $v{\displaystyle {}_{}}$ ${\displaystyle 1_{}}$= ${\displaystyle c}$/ ${\displaystyle {n\mathrm{}}_{}}$ ${\displaystyle 1{}_{}}$. ${\displaystyle v_{1\!$$}}=c/n_{1}\,.}$ 마찬가지로$$ v ${\displaystyle {2\mathrm{}}_{}}$= c${\displaystyle }$/ ${\displaystyle {n\mathrm{}}_{}}$ ${\displaystyle 2{}_{}}$. ${\displaystyle v_{2}=c/n_{2}\.}$ 이러한 대체품을 Eqs. (1)과$$ (2)에서 구한다.

${\displaystyle n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}}:$

(3)

그리고

${\displaystyle \theta _{\text{c}}=\arcsin(n_{2}/n_{1})\,}$

(4)

Eq. (3)은 굴절률 측면에서 일반 매체에 대한 굴절률의 법칙으로, 만일₁ and과 θ이₂ 이음각으로 취해진다면, n과₁₂ n은 방향에서 독립되는 반면, θ과₁ θ은₂ 광선의 발생과 굴절 각도로 취해질 수 있고, Eq. (4)는 다음과 같다.따라서 등방성 매체의 경우 Eqs. (3)과 (4)가 함께 그림 5의 동작을 설명한다.

Eq. (4)에 따르면 물(n₁ ≈ 1.333)에서 공기(n₂ ≈ 1)까지의 발병률은 θ_c 48.6°인 반면, 일반 유리나 아크릴(n₁ ≈ 1.50)에서 공기(n₂ ≈ 1)까지의 발병률은 θ_c 41.8°인 것으로 나타났다.

θ을_c 산출하는 아크신 함수는 n₂ ≤n₁ (${\displaystyle {v\mathrm{}}_{}}$ 2 ${\displaystyle {}_{}}$ ${\displaystyle {v\mathrm{}}_{}}$ ${\displaystyle {}_{}}$)${\displaystyle }$. ${\displaystyle (v_{2}\geq v_{1}}\,}$만 정의되므로 등방성 매체의 경우 두 번째 매체가 첫 번째 매체보다 굴절률(정상 속도 낮음)이 높은 경우 전체 내부반사가 발생할 수 없다.예를 들어, 공기에서 물까지의 발생에 대한 TIR은 있을 수 없다. 오히려 물에서 공기까지의 발생에 대한 임계 각도는 공기에서 물까지의 방목 발생 시 굴절각이다(그림 6).^[10]

굴절률이 높은 매체는 일반적으로 광학적으로 밀도가 높고 굴절률이 낮은 매체는 광학적으로 희귀하다고 기술된다.^[11]따라서 "감지 투 레이어" 발생에는 전체 내부 반영이 가능하지만 "감지 투 레이어" 발생에는 가능하지 않다고 한다.

일상적인 예

수족관 옆에 눈을 수위 이하로 두고 서 있을 때, 물고기나 물에 잠긴 물체가 수면에 비치는 것을 볼 수 있다(그림 1).반사된 이미지의 밝기(직접 보기처럼 밝음)는 놀라울 수 있다.

수면 바로 밑에서 수영하다가 눈을 뜨면 비슷한 효과를 볼 수 있다.물이 잔잔하면 임계각(수직에서 측정) 밖의 표면은 거울처럼 나타나 아래 물체를 반사한다.물 위의 영역은 위쪽을 제외하고는 볼 수 없는데, 반구형 시야는 각 직경이 임계각(cf)의 2배인 스넬의 창으로 알려진 원뿔형 장으로 압축된다.그림 6).^[12]그 물의 위에 있는 경치는 분야는 이론적으로 180도지만 우리가 가까운 지평선까지 보이지 않기 때문에, 수직 치수 더 강하게 굴절로 압축된 것 같은 방정식(3)에 의해 90도,가 80도, 70°의 air-to-water 사건에 대한, 굴절의 해당 각도 48.6°(그럼 4.1에 나타나 θcr. 6), 47.6°, 44.8°에 사용되고 있다.수평선 위 20° 지점의 이미지는 스넬의 창 가장자리에서 3.8°인 반면 수평선 위 10° 지점의 이미지는 가장자리에서 1°밖에 떨어져 있지 않음을 나타낸다.^[13]

예를 들어 그림 7은 수영장의 얕은 끝의 바닥 근처에서 찍은 사진이다.오른쪽 벽의 넓은 수평 줄무늬처럼 보이는 것은 주황색 타일 줄의 아래쪽 가장자리와 그 반사로 이루어져 있다. 이것은 물의 높이를 표시하며, 다른 벽을 가로질러 추적될 수 있다.수영선수는 그녀의 반사의 아랫부분을 뒤틀며 사다리(오른쪽)의 반사를 왜곡했다.그러나 대부분의 표면은 여전히 고요하여, 타일이 깔린 수영장 바닥이 선명하게 비치고 있다.물 위의 공간은 프레임의 윗부분을 제외하고는 보이지 않는데, 그 안에서는 사다리의 손잡이가 스넬의 창문 가장자리 위에서만 분간할 수 있다. 그 안에서는 수영장 바닥의 반사가 부분적일 뿐, 사진에서는 여전히 눈에 띈다.굴절률의 변화로 인해 스넬 창 가장자리의 색상 주름도 파장으로 식별할 수 있다(분산 참조).

임계 각도는 원석이 깎이는 각도에 영향을 미친다.예를 들어 라운드 '브릴리언트' 컷은 앞 면에 발생한 빛 사건을 굴절시켜 TIR로 뒷면 면으로부터 반사시켜 다시 앞면을 통해 밖으로 내보내 돌이 밝게 보이도록 설계됐다.다이아몬드(그림 8)는 굴절률(약 2.42)이 높고 결과적으로 임계각(약 24.5°)이 작기 때문에 특히 이 치료에 적합하다.시야각의 넓은 범위에서 바람직한 행동을 ^[14]하다이와 비슷하게 처리될 수 있는 값싼 재료로는 입방 지르코니아(지수 ≈ 2.15)와 모이사나이트(비등방성, 따라서 이중 굴절성, 방향과 양극화에 따라 ^{[Note 4]}약 2.65~2.69의 지수를 갖는 것)가 있다. 따라서 이 두 가지 모두 다이아몬드 시뮬러로 인기가 있다.

관련 현상

반사파(질적 설명)

수학적으로 파장은 시간이 걸리는 분야로 설명되며, "필드"는 우주에서 위치의 함수가 된다.전파파에는 "이퍼트"장과 "흐름"장이 필요하며, 후자는 벡터(우리가 2차원에서 또는 3차원으로 작업하는 경우)가 된다.노력과 흐름의 산물은 힘과 관련이 있다(시스템 동등성 참조).예를 들어, 비시성 유체의 음파의 경우, 힘 필드를 압력(스칼라)으로, 흐름 장을 유체 속도(벡터)로 취할 수 있다.이 두 개의 산물은 강도(단위 면적당 전력)이다.^{[15][Note 5]}전자파의 경우, 우리는 노력장을 전기장 E 로 하고 흐름장을 자화장 H로 삼아야 한다. 이 두 가지 모두 벡터로서, 벡터 생산물은 다시 강도다(Poynting vector 참조).^[16]

(say) 매체 1의 파동이 매체 1과 매체 2의 인터페이스에서 반사되었을 때, 매체 1의 흐름 장은 사건 및 반사 파동으로 인한 흐름장의 벡터 합이다.^{[Note 6]} 반사가 비스듬한 경우 입사 및 반사 필드는 반대 방향에 있지 않으므로 인터페이스에서 취소할 수 없다. 반사가 총체적이더라도 (위치 및 시간의 함수로서) 결합 필드의 일반 구성요소 또는 접선 구성요소 중 하나가 인터페이스에 인접하여 0이 아니어야 한다.더욱이, 필드를 지배하는 물리적 법칙은 일반적으로 두 요소 중 하나가 인터페이스를 가로질러 연속된다는 것을 의미할 것이다(즉, 우리가 인터페이스를 통과할 때 갑자기 변하지 않는다). 예를 들어 전자파의 경우, 접점 조건 중 하나는 서파가 없으면 H의 접선성분이 연속적이라는 것이다.ce ^[17]전류따라서 반사가 총체적이더라도 중간 2로 된 흐름장이 어느 정도 침투해야 하며, 이는 노력 및 흐름 영역에 관한 법률과 결합하여 노력 영역의 침투도 어느 정도 있을 것임을 암시한다.동일한 연속성 조건은 중간 2에서 필드의 변동("warvity")이 사건 및 중간 1에서 반사파와 동기화됨을 의미한다.

그러나 반사가 전체일 경우, 중간 2에 대한 필드의 공간 침투는 어떻게든 제한되어야 하며, 그렇지 않으면 전체 범위와 해당 필드의 총 에너지가 계속 증가하여 중간 1에서 동력을 빼내야 한다.연속파열차의 총반사는 일부 에너지를 중간 2에 저장할 수 있도록 허용하지만 중간 1에서 중간 2로의 지속적인 동력 전달은 허용하지 않는다.

따라서,대부분의질적 추론을 이용하여, 우리는 전체 내부 반사가"외부"매체에 와블리크 필드와 함께 수반되어야 하며, 사건 및 반사 파동과 동시에 인터페이스를 따라 이동해야 하지만,"외부"매체에 대한 공간 침투가 제한되어 있다. 그러한 필드는"외부"매체에 대한 일종의 제한적 공간 침투로, 그러한 필드를"에바"라고 부를 수 있다.백열 파동

그림 9는 기본적인 생각을 보여준다.입사파는 평면과 사인파로 가정한다.단순함을 위해 반사된 파동은 보이지 않는다.반사파는 사건 및 반사파와 함께 우측으로 이동하지만 인터페이스와의 거리가 늘어나면서 진폭이 떨어진다.

(그림 9의 반사파의 두 가지 특징은 나중에 설명해야 한다: 첫째, 반사파 볏이 인터페이스에 수직이라는 것, 둘째, 반사파가 입사파보다 약간 앞서 있다는 것).

FTIR(파쇄된 총 내부 반사)

내부 반사가 총체적이어야 할 경우, 반사파가 전환되지 않아야 한다.예를 들어 특정 발생각에서 유리( 굴절률이 높은 경우)에서 공기(굴절률이 낮은 경우)에 이르는 전자파가 TIR의 대상이 된다고 가정해 보자.그리고 만약 세 번째 매개체가 두 번째 매개체를 대체한다면, 동일한 발생 각도에 대해 표준 전송 파동트레인을 얻을 수 있을 정도로 굴절률이 충분히 높은 세 번째 매개체(흔히 첫 번째 매개체와 동일)가 있다고 가정해 보십시오.그 다음, 세 번째 매체를 첫 번째 매체의 표면에서 몇 파장의 거리 내에 가져오면, 두 번째 매체에 유의한 진폭을 갖는 반사파가 세 번째 매체로 효과적으로 굴절되어 세 번째 매체로 0이 아닌 전달을 하게 되고, 따라서 총 리플렉보다 작다.제1중간으로 ^[18]되돌아가다전파의 진폭이 공극에 걸쳐 감소함에 따라, 전송된 파동은 감쇠되어 전송이 적으며 따라서 갭이 없는 것보다 더 많은 반사가 발생한다. 그러나 어느 정도의 전송이 있는 한, 반사는 전체보다 적다.이러한 현상을 좌절된 총체적 내부반사(여기서 "분해"는 "총체"를 부정하며, 약칭 "분해 TIR" 또는 "FTIR"라고 부른다.

좌절된 TIR은 손에 들고 있는 물컵의 윗부분을 들여다보면 알 수 있다(그림 10).유리를 느슨하게 고정하는 경우 접촉이 눈에 띄는 효과를 내기 위해 충분히 가깝지 않고 광범위하게 접촉할 수 있다.그러나 그것이 좀더 단단하게 잡히면, 지문의 굴곡은 반사되는 유리공기 표면을 통해 그 굴곡들을 볼 수 있도록 하면서, 반사되는 파도와 강하게 상호작용한다.^[19]

파라핀 왁스를 "내부" 매질(사건과 반사파가 존재하는 곳)으로 사용하여 전자레인지로도 동일한 효과를 증명할 수 있다.이 경우 허용되는 간격 폭은 (예:) 1 cm 또는 몇 cm일 수 있으며, 쉽게 관측할 수 있고 조정할 수 있다.^[1][20]

좌절된 TIR이라는 용어는 반사 인터페이스에 충분히 가까운 물체에 의해 반사파가 산란되는 경우에도 적용된다.이 효과는 인터페이스로부터의 거리에 산란 빛의 양이 강하게 의존하는 것과 함께, 총체적인 내부 반사 현미경에서 이용된다.^[21]

FTIR의 메커니즘은 반사파 커플링이라고 불리며, 양자 터널링의 직접 가시적인 예다.물질의 파동 특성 때문에, 고전 역학에서 에너지가 불충분하다고 말할지라도, 전자는 장벽을 통해 "터널링"할 확률은 0이 아니다.^[18][19]마찬가지로 광자는 빛의 파동 특성 때문에 광자가 접근하는 방식이 너무 비스듬하다고 말할 수 있더라도 간격을 통과할 확률은 0이 아니다.

내부 반사가 임계 각도를 넘어서도 전체보다 적을 수 있는 또 다른 이유는 외부 매체가 "손실"(완전히 투명하지 않은)일 수 있기 때문인데, 이 경우 외부 매체는 반사파로부터 에너지를 흡수하여, 반사파의 유지로 인해 입사파로부터 동력을 끌어모을 것이다.결과적으로 총 반사율보다 적게 반사되는 것을 ATR(감쇠된 총 반사율)이라고 한다.이 효과, 특히 흡수의 주파수 의존성은 알 수 없는 외부 매체의 구성을 연구하는 데 사용될 수 있다.^[22]

발진파 유도

균일한 평면 사인파 전자파에서 전기장 E는 형태를 가진다.

${\displaystyle \mathbf{E_{k} e^{i(\mathbf {k\cdot r} -\omega t)},}$

(5)

여기서 E는_k (정수) 복합 진폭 벡터, i는 상상 단위, k는 파동 벡터(hose requency k는 각도 와바넘버, r는 위치 벡터, Ω은 각도 주파수, t는 시간이며, 표현식의 실제 부분은 물리장이라고 이해된다.^{[Note 7]}자화장 H는 k와 Ω이 동일한 형태를 가지고 있다.위치 r이 k와 정상적인 방향으로 변화할 경우 식 값은 변경되지 않으며, 따라서 k는 파형에서 정상이다.

If ℓ is the component of r in the direction of k, the field (5) can be written ${\displaystyle \mathbf {E_{k}} e^{i(k\ell -\omega t)}\,.}$ If the argument of ${\displaystyle e^{i(\cdots )}}$ is to be constant, ℓ must increase at the velocity ${\displaystyle \omega /k\,,$위상 속도라고 알려진$$ $\,}.$^[23]이 값은${\displaystyle }c{\displaystyle }$ /${\displaystyle n}$ ,$${\$displaystyle c/n\\}$과 동일하며 여기서 c는 참조 매체의 위상 속도(진공기로 간주됨)이고 n은 기준 매체의 국부 굴절률이다.k에 대한 해결은 $k{\displaystyle }$= ${\displaystyle n}$ ${\displaystyle \Omega }$/ ${\displaystyle c,}$ ${\$=n$\omega /c\\,}$을(를) 준다.

${\displaystyle k=filename_{0}\...}$

(6)

여기서 ${\displaystyle k{}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$= ${\displaystyle \Omega }$/ ${\displaystyle c}$ ${\$은(는) 진공 상태의 wavenumber이다$$.^{[24][Note 8]}

(5)부터 "외부" 매체의 전기장에는 형태가 있다.

${\displaystyle \mathbf {E} _{\text{t}} _{\mathbf {k}{\text{t}}}e^{i(\mathbf {k_{t}\cdot r} -\omega t)}\}\}$

(7)

여기서 k는_t 전달 파형에 대한 파동 벡터(우리는 등방성 매체를 가정하지만, 전송된 파동은 아직 전파를 방출한다고 가정하지 않는다.

데카르트 좌표(x, y,z)에서 영역 y < 0을 굴절률 n으로₁ 하고 영역 y > 0을 굴절률 n으로₂ 한다.그러면 xz 평면이 인터페이스고, y축이 인터페이스에 대해 정상이다(그림 11).i와 j(볼드 로마식)를 각각 x와 y 방향의 단위 벡터가 되게 한다.발생 평면(사건 파동 정규 및 인터페이스에 대한 정규 포함)을 xy 평면(페이지의 평면)으로 하고 발생 각도 θ을_i j에서 i로 측정한다.같은 의미로 측정된 굴절각은 θ_t(전송된 경우 t, 반사된 경우 r을 보존함)이 되도록 한다.

(6)로부터 송신파 벡터 k는_t 진도 nk를₂₀ 가진다.그래서 기하학에서 보면

마지막 단계가 스넬의 법칙을 사용하는 곳이지위치 벡터로 도트 제품을 가져가면Eq. (7)가 될 수 있도록

${\displaystyle \mathbf {E} _{\text{t}}=\mathbf {E} _{\mathbf {k} {\text{t}}\,}e^{i(n_{1}k_{0}x\sin \theta _{\text{i}}+n_{2}k_{0}y\cos \theta _{\text{t}}-\omega t)}.}$

(8)

TIR의 경우 angle_t 각도는 통상적인 의미에서는 존재하지 않는다.그러나 우리는 cos θ을_t 복잡하게 허용함으로써 전송된 (발진) 파동에 대해 (8)을 여전히 해석할 수 있다.이것은 우리가 죄악의_t 면으로 cos write을_t 쓰고, 그 다음에 스넬의 법칙을 사용하여 죄악의_i 면으로 말할 때 필요하게 된다.

임계 각도보다 큰 θ의_i 경우 제곱근 기호 아래의 값이 음수이므로 다음과 같다^[25].

${\displaystyle \cos \text{t}=\pm i\,{\sqrt {(n_{1}/n_{2})^{2}\sin ^{2}\theta _{\text{i}-1}, .}$

(9)

어떤 부호가 적용되는지 판단하기 위해 (9)를 (8)로 대체하여 (9)를 (8)로 대체하고 (8)을 얻는다.

${\displaystyle \mathbf {E} _{\text{t}}=\mathbf {E} _{\mathbf {k} {\text{t}}\,}e^{\mp {\sqrt {n_{1}^{2}\sin ^{2}\theta _{\text{i}}\,-\,n_{2}^{2}}}\;k_{0}y}\;e^{i{\big (}(n_{1}k_{0}\sin \theta _{\text{i}})x-\omega t{\big )}}\,,}$

(10)

(9)에서 결정되지 않은 기호가 그것과 반대인 경우.전파 전달 파형의 경우, 즉 진폭이 y 증가함에 따라 소멸되는 파형의 경우, (10)의 미결정 부호는 마이너스여야 하므로 (9)의 미결정 부호는 플러스 값이어야 한다.^{[Note 9]}

올바른 기호로 결과(10)를 약칭할 수 있다.

${\displaystyle \mathbf {E} _{\text{t}\propto \,e^{-\cappa y\,}e^{x}x-\omega t)}\}$

(11)

, where

${\displaystyle {\regated}\kappa &=k_{0}\,{\sqrt {n_{1}^{1}^{2}\chin ^{2}\\\\text{i}\,-\,n_{2}^{2}}}}\}\k_{x\!}}&=n_{1}k_{0}\sin \theta _{\text{i}}~,\end{arged}}}$

(12)

그리고 k는₀ 진공상태의 wavenumber이다. ${\displaystyle 즉}$,${\displaystyle \Omega }$ ${\displaystyle /}$ c$$. {\$displaystyle \,\omega$ /c$\,}$

그래서 반사파는 x 방향으로 이동하는 평면 사인파인데, 진폭은 y 방향으로 기하급수적으로 소멸된다(cf).그림 9).이 파동에 저장된 에너지도 마찬가지로 x 방향으로 이동하며 인터페이스를 교차하지 않는다는 것은 명백하다.따라서 Poynting 벡터는 일반적으로 x 방향의 구성요소를 가지고 있지만, 그것의 y 구성요소는 평균 0이다(비일비일비일비일비일비일비일비일비일비일비일비일비일비일비일비일비일비일비일비재).^[26][27]

Eq. (11)는 좌표 y(인터페이스에서 측정)가 d${\displaystyle }$= 1 /${\displaystyle \kappa }$, ${\$ $거리$만큼 증가함에 따라 인자가$$ e만큼 반사파의 진폭이 떨어진다는 것을 나타낸다.^[28](12)의 첫 번째 방정식의 왕복으로, 침투 깊이가^[27]

여기서 λ은₀ 진공에서의 파장이다. 즉, ${\displaystyle 2\mathrm{}}$ ${\displaystyle \pi }$/ ${\displaystyle {k\mathrm{}}_{}}$ ${\displaystyle 0{}_{}}$. ${\displaystyle \,2\pi /k_{0}\,}$분자와 분모를 n 산출량₂ 단위로 나눈다$$^[29]. 여기서 ${\displaystyle \lambda {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$/ ${\displaystyle n{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ $displaystyle \,\displaystyle \,\{2}=\{0}/n_{2}\,}$는 두 번째 (외부) 매체의 파장이다.$따라서{\displaystyle {}_{}}$ ${\displaystyle d_{}}$를 발생각 함수로서 n 1${\displaystyle {}_{}}$/ ${\displaystyle n{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ {\$displaystyle n_{1}/n_{2\,}}$의 다양한 값에 대해 λ₂ 단위로 표시할 수 있다($$그림 12). θ이_ii 임계 각도를 향해 감소하면 분모가 0에 가까워져 예상대로 d가 제한 없이 증가하게 되는데, 이는 critical이 임계보다 작으면 외부 매체에 균일한 평면파가 허용되기 때문이다.θ이_i 90°(그라스팅 발생)에 가까워지면 d는 최소에 접근한다. 물에서 공기로, 또는 일반 유리에서 공기로의 발생의 경우 d는_min 크게 다르지 않다.λ₂/2π. 그러나 d는 발생 각도가 작은 경우(그림 12), 진폭은 여전히 몇 배 d의 거리에서 유의할 수 있다. 예를 들어 e가^−4.6 0.01보다 조금 크기 때문에 인터페이스의 4.6d 거리 내의 발생파 진폭은 인터페이스에서 값의 최소 1%이다.따라서 느슨하게 말하면, 우리는 반사파 진폭이 인터페이스의 "몇 개의 파장" 내에서 유의하다고 말하는 경향이 있다.

위상교대

1817년과 1823년 사이에 아우구스틴-장 프레스넬은 프레스넬 반사 계수가 0이 아닌 가상의 부분을 획득하기 때문에 전체 내부 반사가 비경쟁 위상 변화(0° 또는 180°로 제한되지 않는 위상 변화)를 동반한다는 것을 발견했다.^[30]이제 선형, 균질, 등방성, 비자기성 매체의 경우 전자파에 대한 이러한 영향을 설명하겠다.위상변동은 발생 각도가 임계 각도를 넘어 증가함에 따라 증가하지만, 입사파의 양극화에 따라 달라지는 진전으로 판명된다.

방정식 (5), (7), (8), (10) 및 (11)에서 Ωt를 Ωt+ϕ(즉, -Ωt를 -Ωt-ϕ로 바꾸면 -Ωt를 -Ωt-ϕ로 바꾸면) ϕ 각도로 위상이 진전되며, 그 결과는 (복잡한) 필드에 e를^−iϕ 곱한 것이다.따라서 위상 진전은 음의 논거가 있는 복잡한 상수에 의한 곱셈과 같다.이는$$ (예) 필드(5)가 시간 ${\displaystyle {}_{}}$을 ${\displaystyle {포함}^{}}$하는 $Ek{\displaystyle {\mathbf{}}_{}}$ e k ${\displaystyle {\cdot }^{}}$ ${\displaystyle r^{}{}^{}}$ e${\displaystyle {}^{}}$- ${\displaystyle i^{}}$ ${\displaystyle {\Omega }^{}}$ t${\displaystyle {}^{}}$, ${\$로 인수될 때 더 명백해진다.^{[Note 10]}

입사, 반사 또는 전달 파형의 양극화를 나타내기 위해, 인터페이스에 인접한 전기장은 각각 표면과 입사 평면에 평행인 s와 p 성분으로 알려진 두 개의 수직 구성 요소로 분해될 수 있다. 즉, s와 p 구성 요소는 각각 정사각형이고,발생 ^{[Note 11]}평면에 평행하게

양극화의 각 요소에 대해 입사, 반사 또는 전송되는 전기장(Eq. (5)의 E)은 일정한 방향을 가지며, 그 방향의 (복잡한) 스칼라 성분으로 나타낼 수 있다.그런 다음 반사 또는 전송 계수는 동일한 지점 또는 인터페이스의 반대편에 있는 무한히 분리된 지점에서 복잡한 구성 요소의 비율로 정의될 수 있다.그러나 계수의 기호를 고정하기 위해서는 "방향"에 대한 긍정적인 감각을 선택해야 한다.구성 요소의 경우 분명한 선택은 사건, 반사 및 전송 분야의 긍정적인 방향(예: 그림 11의 z 방향)이 모두 동일하다고 말하는 것이다.p 구성요소의 경우, 본 문서는 사건, 반사 및 전송 분야의 긍정적인 방향이 동일한 매체(예: 그림 11의 빨간색 화살표와 같은 인터페이스의 같은 측면)로 기울어진다는 관례를 채택하고 있다.^{[Note 12]} 그러나 어떤 책들은 p 성분들에 대해 다른 관례를 사용함으로써 반사 계수에 대한 결과 공식에 다른 기호를 발생시킨다는 것을 독자들에게 경고해야 한다.^[31]

s 양극화의 경우 반사 계수와 투과 계수를 각각_s r과 t로_s 한다.p 양극화의 경우 해당 계수를 r과_p t로_p 한다. 그런 다음 선형, 균질, 등방성, 비자기성 매체의 경우 계수는 다음과 같이 주어진다.^[32]

${\displaystyle r_{s}={\frac {n_{1}\cos \theta _{\text{i}-n_{2}\cos \ta _{n_{1}}}cos \teta _{\text{i}+n_{2}}cos \cos \ta _{2}}\cos \teta _{\text{t}}}}$

(13)

${\displaystyle t_{s}={\frac {2n_{1}\cos \theta _{\text{i}}}{n_{1}}cos \theta _{\text{i}+n_{2}}}\cos \teta _{\text{t}}}}$

(14)

${\displaystyle r_{p}={\frac {n_{2}\cos \teta _{\text{i}-n_{1}cos \teta _{n_{n}}}cos \teta _{\text{i}+n_{1}cos \cos \cos _{1}}\cos \teta _{\text{t}}}}$

(15)

${\displaystyle t_{p}={\frac {2n_{1}\cos \theta _{\text{i}}}{n_{2}}cos \cos \theta _{\text{i}+n_{1}}}\cos \teta _{\text{t}}}\,}$

(16)

(위의 파생은 프레스넬 방정식 § 이론을 참조한다.)

이제 우리는 전송된 파동이 재발한다고 가정한다.올바른 기호(+)를 사용하여 (9)를 (13)로 대체하면

, where즉, n은 "외부" 매체에 상대적인 "내부" 매체의 지수, 또는 외부 매체가 진공인 경우 내부 매체의 지수다.^{[Note 13]} 그래서 r의_s 크기는 1이고, r의_s 주장은의^[33] 단계적 진보를 제공하는

${\displaystyle \s}=\,2\arctan {\fract {n^{2}\sin ^{2}\{2}\chin ^{\text{i}-1}{n\cos \theta _{\text{i}}}}, \cos \cos.}$

(17)

(14)에서 동일한 대체를 할 때 t는_s (복잡한 결합분자 대신) 양의 실제 분자로 r과_s 동일한 분모를 가지며, 따라서_s r의 절반의 인수를 가지므로 반사파의 위상 진전은 반사파의 절반이다.

동일한 기호를 선택하면 (9)을 (15)로 대체하면 다음과 같은 효과를 얻을 수 있다.^{[Note 14]}

그 크기는 1이고, 그 논거는의^[33] 단계적 진보를 제공하는

${\displaystyle \p}=\,2\arctan {\frac {\,n\nqrt{n2}\sin ^{2}\text{i}-1}{\cos \theta \\text _{\i}}}}{\cos \texta _{\i}}}}}\c.}$

(18)

(16)에서 동일한 대체를 이루면서, 우리는 다시 한번 반사파의 위상 진보가 반사파의 절반임을 알게 된다.

방정식 (17)과 (18)은 θ_c θ_i < 90°일 때 적용한다. 여기서 θ은_i 발생 각도, θ은_c 임계 각도 아크신 (1/n)이다. 이 방정식들은 다음과 같은 것을 보여준다.

• 각 위상 진각은 임계 각도에서 0이다(숫자가 0인 경우).
• 각 단계 진전은 180_i°에 근접하며, → →90°
• Δ_pi > Δ의 중간 값 (인자_s n이 (18)의 분자와 (17)^[34]의 분모 안에 있기 때문이다.

θ_i θ의_c 경우, 반사 계수는 방정식 (13)과 (15)에 의해 주어지며, 실재하므로 위상 편이 0°(계수가 양수인 경우) 또는 180°(계수가 음수인 경우)이다.

(13)에서 n ${\displaystyle {2\mathrm{}}_{}}$= n ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle \sin }$ ${\displaystyle }$ ${\displaystyle i_{}}$/ ${\displaystyle \sin {}_{}}$ ${\displaystyle t_{}}$ ${\$스넬의 법칙)를 넣고 분자와 분모를 1/n₁ sin θ을_t 곱하면 얻는다.

${\displaystyle r_{s}=-{\frac {\sin(\theta _{\text{i}-\text{t})}{\sin(\theta _{\text{i}+\text{t}}}}}}}}}}}}$

(19)

이_ti 값은 전송된 광선에 의한 모든 발생 각도에 대해 양성이며 위상 편이 Δ가_s 0이 된다.

(15)와 마찬가지로 하면, 결과는 쉽게 다음과 같은 것으로 나타난다.

${\displaystyle r_{p}={\frac(\theta _{\text{i}-\theta_{\text{t})}{\tan(\tata _\text{i}+\text}}}}}}}}}}$

(20)

이는 작은 각도(즉, 정상 발생에 가까운 경우)에 음수지만, 브루스터 각도에서 변화 기호가 나타나며, 여기서 θ과_i θ은_t 보완적이다.따라서 위상 편이 Δ는_p 작은 θ의_i 경우 180°이지만 Brewster의 각도에서 0°로 전환된다.스넬의 법칙과 상호보완성을 결합하면 밀도 대 레이어 발생에 대한 브루스터의 각도로 angle = 아크탄_i (1/n)이 산출된다.^{[Note 15]}

(등가(19)와 (20)는 프레스넬의 사인 법칙과 프레스넬의 탄젠트 법칙으로 알려져 있다.^[39]둘 다 정상 발생 시 0/0으로 감소하지만, θ_i → 0으로 한계에 정확한 결과를 산출한다.우리가 정상 발병률에 가까워질 때 그들이 반대 신호를 가지고 있다는 것은 이 글에서 사용된 수화 규칙의 명백한 단점이다. 그에 상응하는 장점은 그들이 방목 발생 시 동일한 징후를 가지고 있다는 것이다.)

이로써 모든 발생 각도에 대해 Δ와_s Δ를_p 표시하는 데 필요한 정보가 완성된다.이 작업은 그림 ^[33]13에서 3개의 굴절률에 대해 빨간색 Δ_p, 파란색 Δ로_s 수행된다.입사각도(수평축)에서 브루스터의 각도는 Δ_p(적색)가 180°에서 0°로 떨어지는 지점이며 임계각은 Δ와_p Δ_s(적색 및 청색)가 모두 다시 상승하기 시작하는 지점이다.임계 각도의 왼쪽에는 부분반사 영역이 있으며, 두 반사 계수는 모두 실제(0° 또는 180° 위상)이다.1보다 작은 규모로임계 각도의 오른쪽에는 전체 반사 영역이 있으며, 두 반사 계수는 모두 1과 같은 크기로 복잡하다.해당 영역에서 검은색 곡선은 s 성분에 상대적인 p 성분의 위상 전진을 보여준다.^[40]

굴절률 1.45는 45° 위상 차이를 주기에는 충분하지 않은 반면 1.5의 굴절률로는 약 50.2°와 53.3°의 두 발생각에서 45° 위상 차이를 주기에는 충분하다는 것을 알 수 있다.

이 45° 상대적 이동은 현재 프레스넬 롬브라고 알려진 프레넬의 발명에 사용되며, 두 개의 내부 반사가 입사파의 두 편극화 사이에 90°의 총 상대적 위상 이동을 일으키도록 발생 각도가 선택된다.이 기기는 이뇌동 쿼터파 플레이트와 같은 기능을 수행하지만 무채색(즉, 롬브의 위상변동은 파장에 덜 민감하다)이 더 많다.예를 들어, 두 장치 중 하나를 사용하여 선형 양극화를 원형 양극화(Freshnel도 발견했다)로 변환하거나 그 반대로 변환할 수 있다.

그림 13에서 Δ는 최종 뺄셈으로 계산된다. 그러나 그것을 표현하는 다른 방법이 있다.프레넬 자신은 1823년에 cos Δ에 대한 공식을 주었다.^[41] Born and Wolf(1970, 페이지 50)는 황갈색(Δ/2)에 대한 표현을 도출하고, 분석적으로 최대치를 찾는다.

폭이 유한한 보의 TIR의 경우 발생 각도에 따른 위상 편이변동의 변화는 Gus–를 발생시킨다.Henchen 효과(Henchen effect)는 발생 평면 내에서 반사된 빔의 횡방향 이동이다.^[27][42]이 효과는 s 또는 p 방향의 선형 분극에 적용된다.임베르트-페도로프 효과는 원형 또는 타원형 양극화에 대한 유사한 효과로 발생 평면에 수직으로 이동한다.^[43]

적용들

광섬유는 전체 내부 반사를 이용하여 감쇠가 거의 없는 장거리 신호를 전달한다.^[44]그것들은 통신 케이블과 대장경과 같은 이미지 형성 섬유스코프에 사용된다.^[45]

등대에 사용하기 위해 어거스틴-지안 프레스넬에 의해 발명된 카타디옵티브 프레스넬 렌즈에서, 외부 프리즘은 TIR을 사용하여 순수한 굴절 프리즘으로 가능한 것보다 더 큰 각도를 통해 램프로부터의 빛을 비껴가지만, 기존 미러보다 빛의 흡수(그리고 타르니싱 위험도 적다)^[46]를 덜 가지고 있다.

TIR을 사용하는 다른 반영 프리즘은 다음과 같다(범주 간에 일부 중복된다).^[47]

• 쌍안경 및 점착 스코프의 이미지 보정 프리즘은 쌍체 45°-90°-45° 포로 프리즘(그림 14), 포로-아베 프리즘(Porro-Abbe 프리즘), 인라인 코에니그^[48] 및 압베-코에니그 프리즘, 콤팩트 인라인 슈미트-페찬 프리즘 등이 있다.(마지막은 두 개의 구성요소로 구성되며, 그 중 하나는 바우른프라인드 프리즘의 일종으로, 입사각도가 미미하기 때문에 반사면 두 개 중 하나에 반사 코팅이 필요하다.)이러한 프리즘은 목표 렌즈에서 주요 초점까지 광학 경로를 접어서 주어진 1차 초점 길이의 전체 길이를 줄이는 추가적인 기능을 가지고 있다.
• 천문 망원경을 위해 대각선 모양의 프리즘 별은 단일 포로 프리즘(단일 반사를 위해 구성, 거울 반전 이미지를 제공) 또는 아미치 지붕 프리즘(반전되지 않은 이미지를 제공하는)으로 구성될 수 있다.
• 지붕 프리즘은 날카로운 90° 각도에서 만나는 두 얼굴에서 TIR을 사용한다.이 범주에는 Koenig, Abbe-Koenig, Schmidt-Pechan 및 Amici 유형(이미 언급된 바와 같이)과 SLR 카메라에 사용되는 지붕 펜타프리즘이 포함되며, 이 중 마지막 범주에는 TIR가 아닌 하나의 표면에 반사 코팅이 필요하다.
• 프리즘 코너 반사경은 들어오는 빛의 방향을 반대로 하기 위해 세 개의 총 내부 반사를 사용한다.
• 도브 프리즘은 거울 역행으로 인라인 뷰를 제공한다.

편광 프리즘:선형과 타원형 양극화 사이에서 전환되는 프레스넬 롬은 바이레프링턴트(더블 굴절)는 아니지만, 적어도 직교 양극화의 빛이 부분적으로 전달되는 동안 특정 양극화의 빛이 완전히 반사되는 방식으로 TIR과 바이프링을 결합하는 다른 종류의 프리즘도 있다.예로는 니콜 프리즘, ^[49]글란-이 있다.톰슨 프리즘, 글란-푸코 프리즘(또는 "푸코 프리즘")^[50][51] 및 글란-테일러 프리즘.^[52]

굴절 지수를 측정하는 굴절계는 임계 각도를 사용하는 경우가 많다.^[53][54]

자동 윈드실드/윈드실드 와이퍼용 레인 센서는 윈드실드 외부 표면이 건조할 경우 전체 내부 반사가 적외선 빔을 소스에서 검출기로 유도한다는 원칙을 사용해 구현했지만 표면에 물방울이 떨어지면 빛이 일부 우회한다.^[55]

LCD 컴퓨터 모니터의 백라이팅에 사용되는 엣지 라이트 LED 패널은 TIR을 이용하여 아크릴 유리창에 LED 조명을 고정시킨다. 단, 창 한쪽의 에칭에 의해 일부 조명이 산란되어 거의 균일한 발광성을 낸다.^[56]

총 내부 반사 현미경(THREN)은 반사 인터페이스에 가까운 작은 물체를 조명하기 위해 반사파를 사용한다.그 결과로 발생하는 반사파(TIR 좌절의 한 형태)의 산란은 물체를 "외부" 쪽에서 보면 밝게 보이게 한다.^[21]총내반사 형광현미경(TIRFM)에서는 단순 산란에 의존하는 대신 형광을 유발할 수 있을 정도로 짧은 발산 파장을 선택한다(그림 15).^[57]인터페이스로부터의 거리에 대한 조명의 높은 민감도는 매우 작은 변위 및 힘을 측정할 수 있다.^[58]

빔 분할 큐브는 수신 빔의 힘을 송신 빔과 반사 빔 사이에 나누기 위해 좌절된 TIR을 사용한다.^[18]두 프리즘 사이의 공극(또는 저환산지수 간격)의 폭은 조절이 가능하여 좁은 갭을 위해 더 높은 전송과 낮은 반사율을 주거나 더 넓은 갭을 위해 더 높은 반사율과 더 낮은 전송률을 줄 수 있다.^[59]

광학적 변조는 빠르게 가변적인 갭으로 좌절된 TIR을 통해 이루어질 수 있다.^[60]전송계수는 갭 폭(간격이 거의 닫힐 때까지 함수가 대략 기하급수적이므로, 이 기법은 큰 동적 범위를 달성할 수 있다.

광학 지문인식 장치는 좌절된 TIR을 사용해 잉크(cf)를 사용하지 않고 사람의 지문 이미지를 기록해왔다.그림 11).^[61]

보행 분석은 좌절된 TIR을 고속 카메라와 함께 사용하여 발자국을 포착하고 분석하면 된다.^[62]

녹내장 진단을 위해 안과와 안과에 사용되는 고니오스코프는 홍채와 각막 사이의 각도를 조사하기 위해 TIR을 억제한다.이 보기는 보통 각막-공기 인터페이스에서 TIR에 의해 차단된다.Gonioscope는 공기를 더 높은 지수 매질로 대체하여 비스듬한 발생 시 전송을 허용하며, 일반적으로 TIR을 사용하여 그 자체가 구현될 수 있는 "미러"에 반사된다.^[63][64]

역사

디스커버리

의심스러운 유용성이 있는 무지개의 Theodoric 프레이 버그 시(1304년과 1310년 사이에 쓰여진)[65]과 Kamāl에 의해 놀랍게, 주로 정확한 포괄적인 설명 al-Dīn al-Fārisī(1309년까지 완성되)[66]가끔은 전반사(전술 신문)과 관련에서 언급된 때문에 햇볕을 sph의 내부 반사.rerical인드롭은 전부가 아니다.^{[Note 16]}그러나 칼 벤자민 보이어에 따르면, 무지개에 대한 테오도리어의 논문에서도 다섯 가지 원인에 따라 광학 현상을 분류했는데, 그 중 마지막은 "두 가지 투명한 매체의 경계에 대한 총반사"^[67]라고 했다.테오도리어의 작품은 1814년 조반니 바티스타 벤투리에 의해 재발견되기 전까지 잊혀졌다.^[68]

테오도리어가 무명으로 전락한 것은 일반적으로 TIR의 발견이 요하네스 케플러의 소행으로 1611년 자신의 디옵트리체(Dioptrice)에 자신의 연구 결과를 발표했기 때문이다.케플러는 비록 진정한 굴절의 법칙을 찾지는 못했지만 실험을 통해 공기와 유리 사이의 발생에 대해 입사각과 굴절선이 발생점에 대해 같은 의미로 회전하고, 발생각도가 ±90°까지 변화함에 따라 (지금 우리가 부르는 대로) 굴절각은 ±42°까지 변화한다는 것을 보여주었다.그는 또한 그 사건과 굴절된 광선이 서로 교환할 수 있다는 것을 알고 있었다.그러나 이러한 관측은 42° 이상의 각도에서 유리에서 공기로 광선이 발생하는 경우를 다루지 않았고, 케플러는 즉각적으로 그러한 광선은 반사될 수 있을 뿐이라고 결론지었다.^[69]

르네 데카르트는 굴절의 법칙을 재발견하여 1637년 그의 디옵트리크에 발표하였다.같은 작품에서 그는 사건과 굴절된 광선의 회전 감각과 TIR의 상태를 언급했다.그러나 그는 제한 사건에 대한 논의를 게을리했고, 결과적으로 비판적인 각도에 대한 표현을 하지 못했다.^[70]

Huygens와 Newton: 라이벌 설명

Christiaan Huygens는 그의 빛에 관한 논문 (1690)에서 입사 광선이 "다른 투명한 물질로 침투할 수 없는" 문턱에 많은 주의를 기울였다.^[71]그는 임계각에 대해서는 이름도 대수표현도 하지 않았지만, 유리 대 공기와 수 대 공기의 발생에 대해서는 수치적인 예를 들었고, 임계 각도에 가까운 발생각도의 작은 변화에 굴절각의 큰 변화를 주목했으며, 이를 재의 밝기가 급격히 증가하는 원인으로 꼽았다.굴절된 광선이 접점에 닿는 접선에 접근할 때 굴절된 광선.^[72]Huygens의 통찰력은 현대 이론에 의해 확인된다: 위의 Eqs. (13)와 (15)에서는 θ이_t 90°에 가까워질수록 반사계수가 예외적으로 가파르게 증가한다고 말할 것이 없다. 단, Snell의 법칙에 따르면 θ_t 그 자체가 점점 가팔라지는 θ의_i 함수라는 것을 제외한다.

Huygens는 직선 전파, 반사, 통상적인 굴절의 법칙에 대한 그의 설명과 같은 틀 안에서 TIR에 대한 설명을 제공했고, 심지어 "아이슬랜드 결정"(계산)의 비상한 굴절까지도 제시했다.이 프레임워크는 두 가지 전제에 놓여 있다. 첫째, 전파 전선에 의해 교차되는 모든 지점은 2차 파장의 원천이 된다("Huygens's pronics"). 둘째, 초기 파장을 고려할 때, 파형의 후속 위치는 초기 위치에서 방출되는 모든 2차 파장의 봉투(일반적인 탄젠트 표면)이다.표면의 반사 또는 굴절의 모든 사례는 그 표면에서 방출되는 이차파를 고려하여 간단히 설명된다.더 느린 전파의 매개체에서 더 빠른 전파의 매개체로 굴절되는 경우, 2차 파동프롱트가 두 번째 매개체에서 공통 접선을 형성하는 것이 불가능한 특정 발생 빈도가 있다;^[73] 이것이 지금 우리가 임계 각도라고 부르는 것이다.입사 파형 전선이 이 임계 직각도에 근접하면 굴절된 파형은 굴절 표면에 대해 집중되어 첫 번째 매체로 반사되는 2차 파형을 증가시킨다.^[74]

Huygens의 시스템은 심지어 크기가 다른 입자들 사이의 충돌 법칙과 유사하게, 막연하게나마 다른 매체들 사이의 인터페이스에서의 부분 반사를 수용했다.^[75]그러나, 파동 이론이 종파를 계속 가정하는 한, 양극화를 수용할 가능성이 없었으므로, 비범한 굴절의 양극화 의존성이나 ^[76]부분반사계수, TIR의 위상변동을 설명할 기회가 없었다.

아이작 뉴턴은 직선의 전파에 대한 파동 설명을 거부하면서 빛이 파동으로 구성되면 "모든 방향으로 구부려 퍼져나갈 것"이라고 믿었다.^[77]그의 광구체 이론은 직선적 전파를 보다 단순하게 설명하였으며, 그것은 광구체가 인터페이스에 수직으로 작용하는 힘에 종속된다는 가설에서 TIR을 포함한 일반적인 굴절과 반사의 법칙을 설명하였다.^[78]이 모델에서, 밀도 대 레이어 발생의 경우, 힘은 밀도 매체를 향한 유인력이었고, 임계 각도는 접근하는 말뭉치의 정상 속도가 힘 영역의 저쪽에 도달하기에 충분한 발생 각도였다; 더 비스듬한 발생에서는 말뭉치가 뒤로 돌아간다.^[79]뉴턴은 비록 단어로 "사인족들이 굴절을 측정하는 것이기 때문에, 총반사가 시작되는 입사 사인 역시 원의 반지름에 해당된다"^[80]고 했지만, 임계 각도에 대한 공식에 해당하는 것을 주었다.

뉴턴은 두 가지 면에서 후이겐스를 뛰어넘었다.첫째로, 놀랄 것도 없이 뉴턴은 TIR과 분산 사이의 관계를 지적했는데, 백색 광선이 부피성을 증가시키는 유리 대 공기 인터페이스에 접근할 때 가장 강하게 환원되는 광선(광선)이 "전체 반사광"에 의해 가장 먼저 "제거"되고, 그 다음이 덜 환원되는 광선이다.^[81]둘째, 그는 두 개의 프리즘, 즉 한 개의 평면과 다른 한 개의 약간 볼록한 볼록한 면을 함께 배치함으로써 (지금 우리가 말하는 것처럼) 총반사가 좌절될 수 있다는 것을 관찰했다; 그는 말뭉치가 첫 번째 프리즘뿐만 아니라 두 번째 프리즘에도 끌릴 것이라는 것을 주목함으로써 간단히 설명하였다.^[82]

그러나 다른 두 가지 면에서 뉴턴의 체계는 덜 일관적이었다.첫째로, 부분 반사에 대한 그의 설명은 말뭉치와 매체 사이의 예상된 끌림의 힘뿐만 아니라, "쉬운 반사작용의 적합성"과 "쉬운 전달의 적합성"이라는 보다 모호한 가설에도 달려 있었다.^[83]둘째, 비록 그의 말뭉치가 "사이드"나 "폴드"를 가질 수 있을 것으로 짐작되지만, 그 오리엔테이션이 "섬-크리스탈"^[84]에서 말뭉치가 평범하게 굴절을 겪었는지 아니면 비정상적인 굴절을^[85] 겪었는지에 대한 그의 기하학적 설명은 이론적으로 뒷받침되지^[86] 않았고 경험적으로 부정확했다.^[87]

라플라스, 말러스 및 감쇠된 총 반사율(ATR)

윌리엄 하이드 울라스턴은 1802년 런던 왕립 협회에 읽혀진 한 쌍의 논문 중 첫 번째 논문에서 알려진 내부 매체인 "환원력"(환원지수)에서 지수를 측정해야 하는 외부 매체에 대한 발생 임계 각도에 근거한 굴절계 발명을 보고했다.^[54][88]이 장치로 월라스턴은 수많은 재료의 "환원력"을 측정했는데, 그 중 일부는 굴절 각도의 직접 측정이 허용되기에는 너무 불투명했다.그의 논문의 번역은 1803년 프랑스에서 출판되었고, 피에르 시몬 라플레이스의 주목을 받은 것으로 보인다.^[89]

라플레이스가 뉴턴의 굴절 이론을 정교하게 기술한 것에 따르면, 두 동등방성 매체 사이의 평면 인터페이스에서 말뭉치 사건이 인터페이스에 대칭인 힘장(force field)의 영향을 받았다.두 미디어가 모두 투명하다면, 두 번째 미디어에서 필드를 빠져나오기 전에 말뭉치를 뒤로 돌리면 전체 반사가 일어날 것이다.그러나 두 번째 매체가 불투명하다면, 첫 번째 매체를 떠나기 전에 말뭉치를 되돌리지 않는 한 반성은 총체적이지 않을 것이다; 이것은 스넬의 법칙에 의해 주어진 것보다 더 큰 임계 각도를 요구했고, 결과적으로 불투명한 매체에 대한 월라스턴 방법의 유효성을 저해했다.^[90]라플레이스는 임계 각도(TIR에 대한 최소 발생 각도) 측면에서 상대 굴절률에 대한 두 사례를 하나의 공식으로 결합했다.이 공식에는 투명한 외부 매체에 대해 하나의 값과 불투명한 외부 매체에 대해 다른 값을 취하는 파라미터가 포함되어 있었다.라플레이스의 이론은 또한 주어진 물질에 대한 굴절률과 밀도 사이의 관계를 예측했다.^[91]

1807년 라플레이스의 이론은 그의 프로테제인 에티엔-루이 말루스에 의해 실험적으로 시험되었다.주어진 대로 굴절률에 대한 라플레이스의 공식을 취하여 다양한 온도(다양한 밀도)에서 액체(투명) 상태와 고체(불투명) 상태의 굴절률을 측정하는 데 사용함으로써 말루스는 라플레이스의 굴절률과 밀도 사이의 관계를 검증했다.^[92][93]

그러나 라플레이스의 이론은 발생 각도가 그의 변형된 임계 각도를 초과하면 외부 매체가 흡수성이 있더라도 그 반사는 총체적일 것이라는 것을 암시했다.분명히 이것은 잘못되었다: 위의 Eqs. (12)에서는 κ이 무한하게 되는 각도_i threshold의 임계값이 없으므로, 발산파(1/³)의 침투 깊이는 항상 0이 아니며, 외부 매체는 조금이라도 손실되면 반사를 약화시킨다.말러스가 분명 불투명한 왁스에 대해 그러한 각도를 관찰한 이유에 대해서는, 우리는 ATR이 시각적으로 TIR과 구별할 수 없을 정도로 반사 감쇠가 작은 특정 각도가 있었다는 것을 유추해야 한다.^[94]

프레스넬 및 위상 편이

프레스넬은 양극화에 대한 연구를 통해 내면의 총체적 반성을 연구하게 되었다.1811년 프랑수아 아라고는 양극화된 빛이 이중-환산 결정의 한 조각을 통과할 때 방향 의존적이고 색에 의존하는 방식으로 "분극화"된 것이 분명하다는 것을 발견했다. 즉, 떠오르는 빛은 분석기(두 번째 편극기)를 통해 볼 때 색깔을 나타냈다.이러한 현상이 불리게 되면서 1812년 장바티스트 비오트에 의해 색채 양극화가 더욱 철저히 조사되었다.1813년, 비오트는 아라고에 의해 연구된 한 가지 사례, 즉 광축에 수직으로 절단된 석영(石z)^[95]은 실제로 거리와 함께 양극화 평면의 점진적인 회전임을 규명했다.

1816년 프레스넬은 파동에 기초한 색소 양극화 이론에 대한 첫 시도를 제안했다.(yet) 명시적으로 횡파를 호출하지 않는 한, 그의 이론은 빛을 수직으로 편극된 두 요소로 구성된 것으로 취급했다.^[96]1817년에 그는 만약 초기에 발생 평면에 대한 급성 각도로 극화되었다면 평면 극화 광선이 전체 내부 반사에 의해 부분적으로 극화되는 것처럼 보인다는 것을 알아챘다.^[97]그는 색-극화 실험에 총체적 내부 반사를 포함시킴으로써 겉으로 보기에 탈극화된 빛이 입사 평면에 평행하고 수직인 편극화된 성분의 혼합물이며, 총반사가 이들 사이의 위상 차이를 도입한다는 것을 알아냈다.^[98]적절한 발생각(아직 정확히 지정되지 않음)을 선택하면 주기의 위상 차이가 1/8로 나타났다."두 개의 결합된 프리즘"의 "병렬 면"에서 나온 두 개의 그러한 반사는 주기의 1/4의 위상 차이를 보였다.그 경우, 초기에 발생과 반사의 평면에 45°로 편광된 경우, 두 개의 반사가 끝난 후 완전히 탈분극화된 것으로 보였다.이러한 발견은 1817년 11월 프랑스 과학 아카데미에 제출되어 낭독된 회고록에서 보고되었다.^[99]

1821년 프레스넬은 자신의 사인 및 탄젠트 법칙(Eqs. (19)와 (20), 위의 20)에 해당하는 공식을 이전에 양극화 평면이라고 불리던 것과 수직인 진동을 가진 횡단 탄성 파형으로 모델링하여 도출하였다.^{[100][Note 17]}그는 오래된 실험 데이터를 사용하여 입사 빔이 발생 평면에 대해 45°로 편광되었을 때 공기로부터 유리나 물까지의 빛 사건에 대해 방정식이 반사 빔의 양극화 방향을 정확하게 예측했음을 즉시 확인했다.^[101]이번 실험확인은 프레스넬이 자신의 성숙한 색채 양극화 이론을 대파적으로 소개한 작품에 대한 '후기'로 보도됐다.^[102]1823년 1월 아카데미에 읽혀진 회고록에서 유래에 대한 자세한 내용이 나중에 제공되었다.^[103]파생은 에너지의 보존과 인터페이스에서의 접선 진동의 연속성을 결합했지만, 진동의 정상적인 구성 요소에서는 어떠한 조건도 허용하지 않았다.^[104]

한편 1822년 12월 제출한 회고록에서 프레넬은 선형 양극화, 원형 양극화, 타원형 양극화라는 용어를 만들었다.^[105][106]원형 양극화의 경우, 두 개의 수직 구성 요소는 1/4 사이클(±90°)이었다.위상이 맞지 않는

새로운 용어는 1823년 1월의 회고록에서 유용했는데,^[103] 사인 및 탄젠트 법칙의 상세한 유래를 포함하고 있었다. 같은 회고록에서 프레스넬은 임계 각도보다 큰 입사각의 경우, 결과 반사 계수가 단위 크기에 따라 복잡하다는 것을 발견했다.그는 평소와 같이 크기가 진폭비를 나타낸다는 점에 주목하면서, 그 주장이 위상변동을 나타낸다고 추측하고, 실험을 통해 가설을 검증했다.^[107]관련된 검증

• 해당 각도에서 다양한 내부 반사의 숫자에 대해 s와 p 성분 사이에 90°의 총 위상 차이를 도입하는 발생 각도 계산(대개 두 개의 해결책이 있었다)
• 입사 평면에 대해 45°의 초기 선형 분극 상태에서 입사 각도에서 총 내부 반사의 개수에 따라 빛을 받는 경우
• 최종 양극화가 순환적이었는지 확인하는 ^[108]것

이 절차는 당시의 기술로는 s와 p의 위상 변동을 직접 측정할 수 없고, 위상 변동의 차이로 야기될 수 있는 등 임의의 양극화 타원성 정도를 측정할 수 없기 때문에 필요했다.그러나 빛의 밝기가 분석기의 방향에 무감각했기 때문에 양극화가 원형인지 확인할 수 있었다.

굴절률이 1.51인 유리의 경우, 프레스넬은 두 반사 계수 사이의 45° 위상 차이(2회 반사 후 90° 차이를 나타냄)가 48°37' 또는 54°37'의 발생 각도를 필요로 한다고 계산했다.그는 롬브를 후각으로 자른 후 그것이 예상대로 작동한다는 것을 알았다.^[109]이리하여 프레스넬 롬의 사양은 완성되었다.마찬가지로 프레스넬은 동일한 각도에서 3회 반사와 4회 반사를 동일한 각도로 한 후 90° 위상 차이를 주는 입사각을 계산하고 검증했다.각각의 경우에는 두 가지 해결책이 있었고, 각각의 경우에서 그는 발생 각도가 클수록 정확한 원형 양극화(반사 평면에 45°의 초기 선형 양극화)가 발생했다고 보고했다.세 가지 반사의 경우 그는 또한 더 작은 각도를 시험했지만, 임계 각도가 가깝고 파장에 약간 의존하기 때문에 약간의 착색 효과를 주었다는 것을 발견했다. (위의 그림 13 비교에서는 위상차 Δ가 더 작은 입사각의 굴절률에 더 민감하다는 것을 보여준다.)

프레넬은 자신감을 더하기 위해 68°27'에서 4개의 총 내부 반사가 2개의 반사가 외부 매체로 물이 있는 반면 나머지 2개는 공기가 있는 경우 반사 표면이 모두 젖었거나 모두 건조하지 않은 경우 정확한 원형 양극화를 줄 것으로 예측하고 검증했다.^[110]

프레스넬의 TIR의 위상변환에 대한 추론은 복합수의 주장에 물리적 의미가 첨부된 첫 번째 사례로 생각된다.이러한 추론은 광파가 전자기라는 것을 알 수 있는 이점이 없이 적용되었지만, 실험의 시험에 통과했고, 제임스 점원 맥스웰이 파동의 추정 성질을 바꾼 후 현저하게 온전하게 살아남았다.^[111]한편 프레스넬의 성공은 1836년부터 시작된 제임스 맥컬라그와 아우구스틴루이 카우치에게 영감을 주어 복잡한 굴절률의 프레스넬 방정식을 이용하여 금속으로부터의 반사를 분석하게 하였다.^[112]복합지수의 가상 부분은 흡수를 나타낸다.^[113]

위의 서술에서 편의상 사용되는 비판각이라는 용어는 시대착오적이다. 그것은 분명히 1873년부터 시작되었다.^[114]

20세기에 양자 전자역학은 광자를 찾을 확률의 관점에서 전자파의 진폭을 재해석했다.^[115]이 프레임워크에서 부분 전송과 좌절된 TIR은 광자가 경계를 통과할 확률을 우려하며, 감쇠된 총 반사율은 광자가 반대쪽에서 흡수될 확률을 우려한다.

Gus-s를 포함한 TIR의 단계적 전환의 보다 미묘한 측면에 대한 연구헨첸과 임베르트-페도로프 효과와 그들의 양자 해석은 21세기까지 계속되었다.^[43]

갤러리

• 

  인도 방아치 한 마리와 물 표면의 총 반사.

• 

  유리잔에 수공기 표면이 붓을 완전히 반사한다.

• 

  와인 잔의 줄기에 녹색 레이저가 완전히 내부로 반사됨.

참고 항목

메모들

참조

참고 문헌 목록

• S. Bochner (1963년 6월), "물리학을 위한 몇몇 기본적인 수학 개념의 중요성," Isis, 54 (2) 179–205; JSTOR 228537.
• M. Born과 E.Wolf, 1970, 광학 원리, 제4대 Ed, 옥스포드: Pergamon Press.
• C.B.보일러, 1959, 레인보우: 신화에서 수학으로, 뉴욕:토마스 요슬로프
• J.Z. Buchwald (1980년 12월), "Huygens에서 Malus까지의 이중 굴절 실험 조사", 정확한 과학의 역사 기록 보관소, 21 (4) : 311–373.
• J.Z. Buchwald, 1989, The Rise of the Wave Theory of the Light, 19세기 초 광학 이론과 실험, 시카고 대학 출판사, ISBN 0-226-07886-8.
• O. Darrigol, 2012, 광학의 역사: 그리스 고대부터 19세기 옥스포드까지 ISBN 978-0-19-964437-7.
• R. 피츠패트릭, 2013, 진동과 파도: 소개, 보카 라톤, FL: CRC 프레스, ISBN 978-1-4665-6608-8.
• R. Fitzpatrick, 2013a, "Total Internal Reflection", 텍사스 대학교 오스틴이 2018년 3월 14일에 접속했다.
• A. 프레스넬, 1866년(에드). H. de Senarmont, E. Verdet, L.프레스넬), 파리 오귀스틴 프레넬:임프레미어 임페리알레 (3권, 1866–70), 제1권 (1866)
• E. 헤흐트, 2017년, 광학, 5차, 피어슨 교육, ISBN 978-1-292-09693-3.
• C. Huygens, 1690년, S.P.에서 번역한 특성 드 라 루미에르 (Leiden: Van der Aa)톰슨 애즈 트리시즈 온 라이트; 프로젝트 구텐베르크, 2005. (cited page number가 1912년 판과 구텐베르크 HTML 판과 일치한다.)
• F.A. 젠킨스와 H.E.White, 1976, Funderstance of Optics, 4th Ed, New York: McGraw-Hill, ISBN 0-07-032330-5.
• T.H. 레빗, 2013, A Short Bright Flash: 어거스틴 프레스넬과 현대 등대의 탄생, 뉴욕: W.W. Norton, ISBN 978-0-393-35089-0.
• 1834년 H. 로이드, 1834년 "물리적 광학의 경과와 현상에 관한 보고", 영국 과학 선진화 협회 제4차 회의 보고서(1834년 에든버러에서 개최), 런던: J. 머레이, 1835년 페이지 295–413.
• I. Newton, 1730, Opticks: 또는, Reflections of the Reflections, Refraction, Inflections 및 Colors of the Light, 4번째 Ed. (런던:William Innys, 1730; Project Gutenberg, 2010); A에 의해 서문으로 재출판되었다.아인슈타인과 E.T.의 소개휘태커(런던:조지 벨 & 선즈, 1931년); I.B.의 추가 서문으로 재인쇄되었다.D.H.D.별 코헨 및 분석 목차롤러, 마이놀라, 뉴욕: 도버, 1952년, 1979년(서문 개정), 2012년. (케이티드 페이지 번호는 구텐베르크 HTML 판과 도버 판과 일치한다.)
• H.G.J. 러튼과 M.A.M 판 벤루이, 1988년 (5회 인쇄, 2002년), 망원경 광학: 아마추어 천문학자들을 위한 종합 매뉴얼, 리치몬드, VA: 윌만벨, ISBN 978-0-943396-18-7.
• J.A. Stratton, 1941년, 전자기 이론, 뉴욕: 맥그로우 힐.
• W. Whewell, 1857년, 귀납 과학의 역사: 초창기부터 현시점까지, 런던: J.W. 파커 & 손, 제2권.
• E. T. Whittaker, 1910, [https://archive.org/details/historyoftheorie00whitrich 에테르와 전기 이론의 역사: 데카르트 시대부터 19세기 클로즈드까지 런던: 롱맨스, 그린 앤 코.

외부 링크

위키미디어 커먼즈에는 Total 내부 반영과 관련된 미디어가 있다.

• Mr. Mangiacapre, "Fluorescence in a Liquid"(비디오, 1m28s)는 2012년 3월 13일에 업로드했다. (퀴닌 물 속 보라색 레이저 빔의 Fluorscence와 TIR)
• 물리학UVM, "Frustrated Total Internal Reflection"(비디오, 37s)은 2011년 11월 21일에 업로드되었다. ("레이저 빔은 안개 낀 플렉시글라스 조각에 전체 내부 반사를 겪는다...")
• SMUPhysics, "Internal Reflection"(비디오, 12s)은 2010년 5월 20일에 업로드했다. ( 45°-90°-45° 프리즘에서 굴절에서 TIR로 변환)