분극면

양극화라는 용어는 선형극화 광선이나 다른 전자기 방사선의 양극화 방향을 가리킨다. 불행히도 이 용어는 두 가지 상반된 의미를 가지고 사용된다. 1811년 에티엔-루이 말루스(Etienne-Louis Malus)가 원래 정의한 바와 같이,^[2] 양극화의 평면은 전파 방향과 자기 벡터를 포함하는 평면과 일치(당시에는 알려지지 않았지만)했다.^[3] 현대문학에서 양극화라는 용어 평면은, 조금이라도 사용된다면, 전기장이 물질과 상호작용하는 경향이 더 크기 때문에 전파 방향과 전기 벡터를 포함하는 평면을 의미할 가능성이 높다.^[4][5]

양방향(더블 리프랙티브) 결정의 파동의 경우, 종래의 정의에 따르면 전파 방향이 일반적으로 다르고 둘 다 자기 벡터에 수직이기 때문에 전파 방향이 광선 방향을 의미하는지 아니면 파동-정상 방향을 의미하는지 또한 명시해야 한다(그림 1). 말루스는 광체의 분자 이론의 부설자로서 오직 광선 방향만을 선택할 수 있었다. 그러나 아우구스틴-지안 프레스넬은 파동 이론(1822년 이후)에 따라 이중 굴절을 설명하려는 그의 성공적인 노력에서, 매체의 예상된 진동이 그 때 일관되게 양극화 평면에 수직이라는 결과와 함께 파동-정상 방향을 선택하는 것이 더 유용하다는 것을 알게 되었다.^[6] 공기와 같은 등방성 매체에서는 광선과 파동-정상 방향이 같으며 프레스넬의 수정은 아무런 차이가 없다.

프레스넬은 또한 수신된 용어에 제약을 받지 않았다면 양극화 평면을 진동과 전파 방향을 포함하는 평면으로 정의하는 것이 더 자연스러웠을 것이라고 인정했다.^[7] 진동의 평면으로 알려지게 된 저 평면은 프레스넬의 "양극화의 평면"과 직각이지만 현대 작가들이 그 이름으로 부르는 평면과 동일하다!

역사적으로 모호하기 때문에 양극화라는 용어는 원저술에서 피해야 한다는 주장이 제기되어 왔다. 특정 필드 벡터의 방향을 쉽게 지정할 수 있으며, 진동이라는 용어조차 양극화 평면보다 혼동의 위험이 적다.^[8]

용어의 물리학

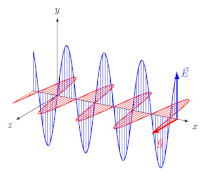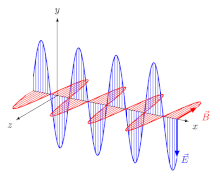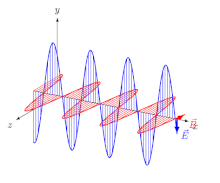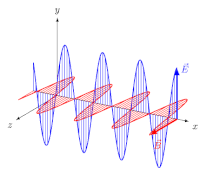
등방성 매체(즉, 방향과 독립적인 성질을 가진 매체)의 전자기파(EM)의 경우, 전기장 벡터(E와 D)는 한 방향으로, 자기장 벡터(B와 H)는 다른 방향으로, 첫 번째 방향과 수직으로, 전파 방향은 전기와 두 방향 모두 수직이다. 자기 벡터 이 경우 전파 방향은 레이 방향과 파동-정상 방향(파형에 직각인 방향)이다. 선형 극성파(평면 극성파라고도 함)의 경우 필드 벡터의 방향이 고정된다(그림 2).

셀 수 없이 많은 재료가 유전체 또는 도체인 반면 상대적으로 극소수만이 페로마그네틱이기 때문에 전자파(빛 포함)의 반사 또는 굴절은 자기성질의 차이보다는 매체의 전기적 특성 차이로 인한 경우가 더 많다. 그러한 상황은 전기 벡터에 주의를 끌기 때문에 우리는 양극화의 방향을 전기 벡터의 방향으로, 그리고 "극화의 평면"을 전기 벡터와 전파의 방향을 포함하는 평면으로 생각하는 경향이 있다.

실제로, 그것은 온라인 브리태니커 백과사전이나 파인만의 양극화에 관한 강연에서 사용되는 관습이다.^[4][9] 후자의 경우 다음과 같은 맥락에서 관례를 추론해야 한다. 파인만은 전기(E) 벡터의 방향을 계속 강조하면서 독자로 하여금 "양극화의 평면"이 그 벡터를 포함하고 있다고 가정하게 하고, 이 해석은 실제로 그가 제시하는 예에 들어맞는다. 무선 신호와 안테나의 양극화를 설명하기 위해 동일한 벡터를 사용한다(그림 3).^[10]

매질이 자성적으로 등방성이지만 전기적으로 비이소성(두 번 감쇄 결정과 같은)인 경우, 자성 벡터 B와 H는 여전히 평행하며 전기 벡터 E와 D는 여전히 양쪽에 수직이며, 광 방향은 여전히 E와 자기 벡터에 수직이며, 파동 정상 방향은 여전히 수직이다. D와 자기 벡터에 연결한다. 그러나 일반적으로 전기 벡터 E와 D 사이에는 작은 각도가 있으므로, 광 방향과 파동-정상 방향 사이에 동일한 각도가 있다(그림 1).^[1][11] 따라서 D, E, 파동-정상 방향, 광선 방향은 모두 같은 평면에 있으며, 그 평면을 "양극의 평면"으로 정의하는 것은 더욱 자연스럽다.

그러나 이러한 "자연적"의 정의는 1860년대에 제임스 서기 맥스웰에 의해 개발된 전자파 이론에 따라 달라진다. 단, 양극화라는 단어는 약 50년 전에 생겨났으며, 이와 관련된 미스터리는 훨씬 더 오래 전으로 거슬러 올라간다.

용어의 역사

후보자 3명

우연히든 설계상이든 양극화 평면은 항상 자기장 벡터와 전파 방향을 포함하는 평면으로 정의되어 왔다. 그림 1에는 참조가 용이하도록 숫자를 지정할 수 있는 세 개의 평면이 있다.

(1) 전기 벡터와 양쪽 전파 방향(즉, 자기 벡터에 대한 평면)을 모두 포함하는 평면,

(2a) 자기 벡터와 파동 정규(즉, D에 정규적인 평면)을 포함하는 평면,

(2b) 자기 벡터와 레이(즉, E에 정상인 평면)를 포함하는 평면.

등방성 매체에서 E와 D는 방향이 같으므로 ^{[Note 1]}광선과 파동 정규 방향이 병합되고 평면(2a)과 (2)b가 다음과 같이 하나가 된다.

(2) 자기 벡터와 양쪽 전파 방향을 모두 포함하는 평면(즉, 전기 벡터에 대해 정규적인 평면)

말루스의 선택

Christiaan Huygens가 "아이슬란드 결정(Iceland crystal)"의 이중 굴절(Icland crystal, 현재 아이슬란드 스파라 불리는 투명 석회석)을 조사하면서 양극화가 발견되었지만, 이름이나 이해되지는 않았다. 그의 <빛에 관한 논문>(1690년)에 실린 그의 발견의 본질은 다음과 같았다. 정상 발생 시 한 개의 광선(좁은 빛의 광선을 의미함)이 유사한 방향의 석회석 결정체 두 개를 통과할 때, 첫 번째 결정에서 나온 일반 광선은 두 번째 결정에서 일반적인 굴절만 겪는 반면, 첫 번째 결정에서 나온 특별한 광선은 두 번째 결정에서 비정상적인 굴절만 겪는다. 그러나 두 번째 결정체가 입사 광선에 대해 90° 회전할 때 역할이 상호 교환되므로, 첫 번째 결정에서 나오는 보통의 광선은 두 번째 결정에서 특별한 굴절만을 겪게 되고, 그 반대도 마찬가지다. 두 번째 결정의 중간 위치에서 첫 번째 결정에서 나오는 각 광선은 두 번째에 의해 이중으로 굴절되어 총 네 개의 광선을 준다; 결정체가 초기 방향에서 수직 방향으로 회전함에 따라 광선의 밝기가 달라져 두 개의 피나만 있는 극단적인 경우 사이에 매끄러운 전환을 제공한다.광선광선광선광선광선을 ^[12]쪼이다

Huygens는 석회석 결정의 주요 부분을 자연 표면과 정규적이고 둔탁한 고체 각도의 축에 평행한 평면이라고 정의했다.^[13] 이 축은 그가 (정확하게) 비상 굴절의 방향을 설명함으로써 스피로이드 이차파의 축과 평행했다.

양극화라는 용어는 1811년 에티엔-루이 말루스에 의해 만들어졌다.^[2] 1808년, 후이겐스의 이중 굴절 기하학적 묘사를 확인하는 와중(그의 물리적 설명을 반박하는 동안) 말러스는 한 줄기 빛이 적절한 각도로 비금속 표면에서 반사될 때, 석회석 결정에서 나오는 두 개의 광선 중 하나처럼 작용한다는 것을 발견했다.^{[14][Note 2]} 이러한 행동은 이전에는 이중 굴절과 관련된 것에서만 알려져 왔기 때문에, 말러스는 그 맥락에서 그것을 기술했다. 특히 그는 편광 광선의 양극화 평면을 일반적인 굴절만 일으키기 위해 석회석 결정의 주요 부분이 놓여 있어야 하는 광선을 함유한 평면이라고 정의했다.^[15] 이 정의는 광선이 반사(동위원소 배지에서 떨어져)에 의해 양극화되었을 때, 양극화의 평면은 발생과 반사의 평면, 즉 입사 광선을 포함하는 평면, 반사 표면에 대한 정상, 편광 반사 광선이라는 것을 의미했기 때문에 더욱 합리적이었다. 하지만, 우리가 지금 알고 있는 것처럼, 이 비행기는 전기 벡터가 아닌 편광 광선의 자기 벡터를 포함하고 있다.^[16]

광선과 자기 벡터의 평면은 위에 번호가 (2b)인 것이다. 양극화 평면에 자기 벡터가 포함되어 있다는 의미는 온라인 메리암 웹스터 사전에 주어진 정의에서 여전히 발견된다.^[17] 줄리어스 애덤스 스트랫튼조차 "E의 관점에서 양극화를 정의하는 것이 관례"라고 말한 뒤 "그러나 광학에서 벡터의 방향은 전통적으로 H와 전파의 축을 모두 포함하는 E에 대한 평면을 의미하는 '극화의 평면'에 의해 지정된다"고 즉각 덧붙인다.^[10] 그 정의는 말루스의 정의와 동일하다.

프레스넬의 선택

1821년 아우구스틴-지안 프레스넬은 광파가 배타적으로 횡방향이기 때문에 특정한 횡방향성을 갖는다는 의미에서 항상 극성을 띠며, 우리가 말하는 비극광은 사실 방향이 빠르고 임의로 변하는 빛이라는 가설을 발표했다.^[18] 광파가 탄성 고형분에서 전단파와 유사하고 굴절률이 더 높은 유황성 에테르 밀도가 더 높은 것에 해당한다고 가정했을 때, 그는 진동이 있다면 두 개의 투명한 등방성 매체 사이의 인터페이스에서 부분반사(반사에 의한 양극화 포함)를 설명할 수 있다는 것을 알았다.에테르들의 이온들은 양극화의 평면에 수직이었다.^[19] 따라서, 수신된 정의에 따르면, 진동이 그 평면에 수직인 경우, 양극화는 특정 평면에 "들어" 있었다.

프레넬 자신도 이 암시가 불편하다는 것을 알았다. 그 해 말 그는 이렇게 썼다.

이 가설을 채택하면서, 진동이 일어나게 되어 있는 편극의 평면을 부르는 것이 더 자연스러웠을 것이다: 그러나 나는 수신된 호칭에 어떠한 변화도 피하고 싶었다.^{[7][Note 3]}

그러나 그는 곧 덜 급진적인 변화를 해야 한다는 의무감을 느꼈다. 그의 성공적인 이중 굴절 모델에서, 매체의 변위는 파동전선과 접선될 수 밖에 없는 반면, 힘은 파동전선에서 이탈할 수 있도록 허용되었다.^[20] 따라서, 만약 진동이 양극화 평면에 수직이라면, 양극화 평면은 파동 보통이지만 반드시 광선은 아니다.^[21] 이중 굴절에 관한 그의 "제2의 회고록"에서 프레넬은 이 새로운 정의를 공식적으로 채택했는데, 이는 공기 같은 등방성 매체의 낡은 정의에 동의한 것이지, 바이어프링겐트 결정에서는 동의한 것이 아니었다는 것을 인정하였다.^[6]

말루스의 양극화 평면에 정상인 진동은 전기적 진동이며, 파전선에 접하는 전기적 진동은 D(그림 1)이다. 따라서 위의 번호 매기기 측면에서 프레스넬은 "양극화 평면"을 (2b)에서 (2a)로 변경했다. 프레넬의 정의는 전파 방향을 지정하지 못하는 메리암-웹스터 정의와 호환된다.^[17] 그리고 그것은 평면(2a)과 (2)b가 (2)로 합쳐지는 등방성 매체의 맥락에서 주어지기 때문에 스트랫튼의 정의와 계속 호환된다.[10]

프레스넬이 '더 자연스러운' 선택이라고 한 것은 D가 들어 있는 평면과 전파 방향이었다. 그림 1에서 그러한 규격을 충족하는 유일한 평면은 "진동의 평면"이라고 라벨을 붙이고 나중에 번호가 매겨진 평면, 즉 현대 저자들이 "양극화의 평면"과 동일시하는 경향이 있는 평면이다. 그러므로 우리는 프레스넬이 그의 전임자들에게 덜 정중하게 굴었기를 바랄지도 모른다. 그러나 그러한 시나리오는 프레넬의 횡파 이론이 일반적으로 받아들여진 후에도 진동의 방향은 계속적인 논쟁의 대상이었기 때문에 보이는 것보다 현실성이 떨어진다.

"진동면"

프레넬의 에테르 드래그 가설에는 굴절률이 에테르 밀도에 따라 좌우된다는 원칙이 필수적이었다.^[22] 그러나 밀도가 방향성이 아니기 때문에 적어도 하나의 굴절률이 방향에 따라 달라지는 2차 굴절률로 확장할 수 없었다. 따라서 굴절에 대한 그의 설명은 양수 매체 내 에테르 강성의 방향적 변화와 더불어 매체 간 밀도의 변화를 필요로 했다.^[23]

제임스 맥컬라흐와 프란츠 에른스트 노이만은 굴절률이 높을수록 항상 밀도는 같지만 탄성 준수(강성이 낮을 경우)가 높다고 가정함으로써 이러한 복잡성을 피했다. 부분반사에 대한 관찰에 동의한 결과를 얻기 위해서는 프레스넬과 달리 진동이 양극화의 평면 내에 있다고 가정해야 했다.^[24]

그 질문은 진동의 방향에 대한 실험적인 결정을 요구했고, 그 도전은 조지 가브리엘 스톡스가 대답했다. 그는 진동면을 "레이를 통과하는 평면과 진동 방향"(^[25]그림 1과 일치)이라고 정의했다. 이제 미세한 회절 그릴이 정상 발생 시 점등된다고 가정해 보십시오. 회절의 큰 각도에서 그링의 방향이 그링의 평면에 평행한 방향으로 붐빌 수 있도록 어느 정도 에지온으로 나타날 것이다. (맥컬라흐와 노이만이 말한 대로) 양극화 평면이 진동 평면과 일치하면 (맥컬라흐와 노이만이 말한 대로) 같은 방향으로 붐빌 것이고, (프레넬이 말한 대로) 양극화 평면이 진동 평면에 정상이라면 양극화 평면은 정상 방향으로 붐빌 것이다. 혼잡의 방향을 찾기 위해서는 입사광의 양극화를 동등한 단계로 변화시킬 수 있고, 분산된 빛의 양극화 평면을 통상적인 방식으로 결정할 수 있다. 스톡스는 1849년에 그러한 실험을 수행했고, 그것은 프레스넬에게 유리하다는 것을 발견했다.^[25][26]

1852년 스톡스는 같은 결론으로 이어지는 훨씬 간단한 실험에 주목했다. 태양으로부터 90° 떨어진 푸른 하늘 조각에서 흩어진 햇빛은, 말루스의 방법에 의해, 시선과 태양을 포함하는 평면에서 양극화되는 것을 발견한다. 그러나 그 빛의 진동이 오직 그 평면과 수직일 수 있다는 것은 기하학에서 명백하다.^[27]

그러나 맥컬라흐와 노이만이 옳다는 감각은 있었다. 비등방성 탄성 고체의 전단파와 자석 등방성이지만 전기적으로 비등방성이 아닌 결정의 전자파 간 유추를 시도한다면 밀도는 자기투과성(둘 다 비방향성이며, 준수성은 전기적 순열성과 일치해야 한다(둘 다 방향성이 된다). 그 결과 고체의 속도는 H장에 해당하므로 전단파의 기계적 진동이 전자파의 자기진동 방향에 있게 된다.^[28] 그러나 스톡스의 실험은 전기적 진동을 감지할 수 밖에 없었다. 왜냐하면 전기적 진동은 물질과 상호작용하는 경향이 더 크기 때문이다. 한마디로 기계적인 아날로그를 가진 것은 맥컬러-뉴만 진동이었지만, 실험에서 검출될 가능성이 높은 것은 프레스넬의 진동이었습니다.^{[Note 4]}

현대적 관행

빛의 전자기 이론은 물질과의 상호작용 때문에 전기적 진동을 더욱 강조했던 반면,^[5] 오래된 "양극화의 평면"은 자기 벡터를 포함하고 있었다. 따라서 전자파 이론은 진동이 양극화 평면에 대해 정상이라는 관습을 강화했을 것이다. 단, 양극화 평면의 역사적 정의에 익숙한 경우였다. 그러나 한 사람이 육체적 고려에만 영향을 받았다면 파인만과^[9] 브리태니카가^[4] 설명하듯이 전기 벡터에 관심을 두고 양극화의 '평면'이 (그런 개념이 필요하다면) 그러한 벡터를 포함하고 있다고 가정할 것이다.

그러나 "양극의 평면"이 필요한 것은 전혀 분명하지 않다: 어떤 필드 벡터가 관여하는지 알고, 특정 벡터의 방향을 지정하여 양극화를 지정할 수 있다. 또는 Born과 Wolf가 제안하는 대로, 그 벡터의 "진동의 평면"을 지정하여 양극화를 지정할 수 있다.^[5] Hecht는 또한 위의 그림 1과 일치하여 E의 평면과 파동-정규로 정의한 진동면(또는 더 일반적으로 진동면)을 선호한다.^[29]

잔여사용

광학적으로 치랄 매체(즉, 파동이 전파되면서 양극화 방향이 점차 회전하는 매체)에서, "양극화 평면"의 정의의 선택은 회전의 존재나 방향("손잡이")에 영향을 미치지 않는다. 이는 양극화라는 용어 평면의 애매함이 더 이상 혼란을 일으키지 않는 하나의 맥락이다.^[30]

원래의 정의가 여전히 그 자체를 암시할 수 있는 정황도 있다. (일반적인 굴절은 없지만 두 굴절 모두 스넬의 법칙을 위반하는) 바이아시알 등급의 비자기성 비-치랄 결정에서, 전기 벡터가 평면에 정상인 경우에 한해 평면 내에서 빛의 속도가 등방성인 3개의 상호 수직면이 있다.^[31] 이러한 상황은 자연스럽게 프레넬이 예상한 진동에 정상적인 평면으로 관심을 끌며, 그 평면은 실제로 프레넬이나 말루스가 정의한 양극화의 평면이다.

그러나 대부분의 맥락에서 전기적 "바이버젼"을 포함하는 평면과 구별되는 "양극화의 평면"의 개념은 논란의 여지가 있을 정도로 중복되어, 확실히 혼란의 원인이 되었다. Born & Wolf의 말에 따르면, "이 용어는 사용하지 않는 것이 좋다."^[32]

메모들

참조

참고 문헌 목록

• W.S. 알디스, 1879년, 프레넬의 이중 굴절 이론에 관한 제2장, 캠브리지: 디튼, 벨 & 코퍼레이션 / 런던: 조지 벨 & 선즈.
• M. Born과 E. Wolf, 1970, 광학 원리, 제4대 Ed, 옥스포드: Pergamon Press.
• J.Z. Buchwald, 1989, The Rise of the Wave Theory of the Light, 19세기 초 광학 이론과 실험, 시카고 대학 출판사, ISBN 0-226-07886-8.
• O. Darrigol, 2012, 광학의 역사: 그리스 고대부터 19세기 옥스포드까지 ISBN 978-0-19-964437-7.
• A. 프레넬, 1822년, 디라 루미에르 (온 라이트), J. 리폴 (에드), Supplément ab la traduation francaise de la cinquieme édition du "Sistéme de Chimie" par Th. 톰슨, 파리: 체즈 메퀴뇽-마르비스, 1822, 페이지 1–137, 535–9; 프레스넬, 1866–70, 제2, 페이지 3–146; T에 의해 번역되었다. Young as "Elementary view of the undulatory theory of light", Quarterly Journal of Science, Literature, and Art, vol. 22 (Jan.– Jun. 1827), pp. 127–41, 441–54; vol. 23 (Jul.– Dec. 1827), pp. 113–35, 431–48; vol. 24 (Jan.– Jun. 1828), pp. 198–215; vol. 25 (Jul.– Dec. 1828), pp. 168–91, 389–407; vol. 26 (Jan.– Jun. 1829), pp. 159–65.
• 1827년 A. 프레넬, "Mémoire sur la double réfraction", Mémoires de l'Academie Royale des Science de l'Institut de France, vol. VII (1824년, 인쇄 1827년), 페이지 45–176; 프레스넬, 1866–70, vol. 2, 페이지 479–596; A.W.에서 번역된 "제2의 메무어…"로 재인쇄되었다. 홉슨은 R에서 "복수 굴절의 추억"으로 묘사되었다. 테일러(ed.), 과학 회고록 V권(London: Taylor & Francis, 1852년), 페이지 238–333. (케이티드 페이지 번호는 번역본에서 가져온 것이다.)
• A. 프레스넬(편집) H. de Senarmont, E. Verdet, L. 프레스넬), 1866–70, 오거스틴 프레스넬(3권), 파리: 임페리얼 임페리얼; 제1권(1866), 제2권(1868), 제3권(1870)
• E. 헤흐트, 2017년, 광학, 5차, 피어슨 교육, ISBN 978-1-292-09693-3.
• C. Huygens, 1690년, S.P.에서 번역한 특성 드 라 루미에르 (Leiden: Van der Aa) 톰슨 애즈 트리시즈 온 라이트; 프로젝트 구텐베르크, 2005. (cited page number가 1912년 판과 구텐베르크 HTML 판과 일치한다.)
• B. 파월(1856년 7월), "반사 및 굴절된 빛에 대한 프레스넬의 공식과 그 적용에 대하여," 철학적 잡지와 과학 저널, 시리즈 4, 12권, 76호, 페이지 1-20.
• J.A. Stratton, 1941년, 전자기 이론, 뉴욕: 맥그로우 힐.
• E. T. Whittaker, 1910, 에테르와 전기 이론의 역사: 데카르트 시대부터 19세기 클로즈드까지 런던: 롱맨스, 그린 앤 코.