시간 논리

논리학에서, 시간 논리학은 시간의 관점에서 자격이 있는 명제들을 표현하고 추론하기 위한 규칙과 상징성의 체계이다.그것은 때때로 한스 캄프의 중요한 공헌과 함께 Arthur Prior가 1950년대 말에 도입한 시간 논리의 모달 논리 체계인 긴장 논리를 언급하는 데 사용되기도 한다.이것은 컴퓨터 과학자, 특히 Amir Pnueli와 논리학자들에 의해 더욱 발전되었습니다.

시간적 논리는 하드웨어 또는 소프트웨어 시스템의 요구사항을 기술하는 데 사용되는 공식 검증에서 중요한 응용 프로그램을 발견했습니다.예를 들어, 요청이 있을 때마다 리소스에 대한 액세스는 최종적으로 허용되지만 두 개의 요청자에게 동시에 부여되지는 않는다고 말할 수 있습니다.이러한 진술은 시간 논리로 쉽게 표현될 수 있다.

동기

"나는 배고프다"는 말을 생각해 보세요.시간의 의미는 일정하지만 문장의 진실 값은 시간에 따라 달라질 수 있습니다.때로는 진실이고 때로는 거짓이지만, 결코 진실과 거짓은 아니다.시간 논리학에서, 진술은 시간에 따라 변화하는 진실 값을 가질 수 있다. 즉, 시간 논리와는 대조적으로, 진실 값이 일정한 진술에만 적용된다.시간 경과에 따른 진실-값의 이러한 처리는 시간적 논리와 계산적 동사 논리를 구별한다.

시간 논리는 항상 연대표에 대해 추론할 수 있는 능력을 가지고 있다.이른바 선형 "시간 논리"는 이러한 유형의 추론에 한정됩니다.다만, 브랜치 로직에서는, 복수의 타임 라인이 원인일 가능성이 있습니다.이것은 예측할 수 없는 동작을 하는 환경을 전제로 하고 있습니다.예를 들어 분기 논리에서 "내가 영원히 배고픔을 유지할 가능성이 있다"와 "결국 나는 더 이상 배가 고프지 않을 가능성이 있다"고 말할 수 있다.만약 우리가 내가 먹여살릴지 안 먹을지 모른다면, 이 진술들은 모두 사실일 수 있다.

역사

비록 아리스토텔레스의 논리가 거의 전적으로 범주형 삼단 논리의 이론과 관련이 있지만, 그의 작품에는 현재 시간 논리의 예상으로 보여지는 구절들이 있고, 1차 시간적 모달 이원 논리의 초기, 부분적으로 발전된 형태를 암시할 수 있다.아리스토텔레스는 특히 미래의 사건에 대한 진술, 즉 ^[1]"내일 해전이 있을 것"과 같은 미래의 사건에 대한 진술이 진실인지 거짓인지를 결정할 수 있는 쌍가성의 원칙이 적용되는 것을 받아들일 수 없었던 미래의 우발상황에 대해 우려했다.

Charles Sanders ^[2]Peirce는 19세기에 다음과 같이 말했습니다.

시간은 논리학자들에 의해 보통 '초논리적인' 물질로 여겨져 왔다.나는 이 의견을 공유한 적이 없다.그러나 나는 논리가 그 형태의 시간적 수정의 도입이 큰 혼란을 초래하지 않는 발전 상태에 이르지 못했다고 생각해왔다; 그리고 나는 아직 그러한 사고방식의 많은 부분을 가지고 있다.

놀랍게도, 우리가 아는 한, 최초의 시간 논리 체계는 20세기 전반에 구축되었다.Arthur Prior는 시간논리의 창시자로 널리 알려져 있지만, 이러한 논리의 첫 공식화는 1947년 폴란드의 논리학자 Jerzy ^[3]oś에 의해 제공되었습니다.Podstawy Analizy Metodologicalznej Kanonow Milla(밀의 방법론 분석 기반)에서 그는 밀의 규범을 공식화했다.Wo'의 접근법에서는 시간 요인에 중점을 두었다.그러므로, 그의 목표에 도달하기 위해, 그는 시간 함수의 공식화를 위한 수단을 제공할 수 있는 논리를 만들어야 했다.이 논리는 인식론적 논리에서 후에 우의 발명에 사용된 최초의 위치 논리였지만 우의 주요 ^[4]목적의 부산물로 볼 수 있었다.논리 자체는 모달 연산자를 사용하는 Prior의 시제 논리와는 매우 다른 구문을 가지고 있습니다.Wo'의 논리언어는 오히려 위치논리에 특유한 실현연산자를 사용하며, 그 표현은 그것의 진실-값이 고려되는 특정 문맥과 결합된다.Wo'의 연구에서 이 고려된 문맥은 시간적인 것에 불과했고, 따라서 표현은 특정한 순간이나 시간 간격과 결합되었다.

그 후 몇 년 동안 아서 프라이어의 시간 논리 연구가 시작되었다.^[4]그는 자유의지와 운명의 철학적 함의를 염려했다.그의 아내에 따르면, 그는 1953년에 시간 논리를 공식화하는 것을 처음 고려했다고 한다.그의 연구 결과는 1954년 ^[4]웰링턴에서 열린 학회에서 처음 발표되었습니다.Prior가 제시한 시스템은 1955년이 되어서야 Prior의 ^[4]형식 논리 부록 1의 마지막 섹션에서 Wo'의 연구를 명시적으로 언급했지만 구문학적으로 Wo'의 논리와 유사했다.

프리어는 1955-6년에 옥스퍼드 대학에서 이 주제에 대해 강의를 했고 1957년에 시간과 모달리티라는 책을 출판했는데, 그는 F와 P라는 두 개의 시간적 연결사(모달 연산자)를 가진 명제적 모달 논리를 소개했는데, 이 책에서 그는 "미래의 어느 때"와 "과거의 어느 때"에 대응했다.이 초기 작업에서 Prior는 시간을 선형으로 간주했습니다.그러나 1958년, 그는 Saul Kripke로부터 편지를 받았는데, 그는 이 가정이 아마도 타당하지 않다고 지적했다.컴퓨터 과학에서 비슷한 발전의 전조가 된 Prior는 이것을 숙고하여 Ockhamist와 ^[2]^{[clarification needed]}Peircean이라고 부르는 두 가지 분기 시간 이론을 개발했다.1958년과 1965년 사이에 프리어는 찰스 레너드 햄블린과도 일치했고, 이 분야의 많은 초기 개발은 예를 들어 햄블린의 의미에 따라 추적될 수 있다.프리어는 1967년에 이 주제에 관한 그의 가장 성숙한 작품인 "과거, 현재, 그리고 미래"를 출판했다.그는 2년 ^[5]후에 죽었다.

긴장된 논리와 함께 Prior는 ^[6]몇 가지 위치논리 체계를 구축했고, 이는 Woś로부터 그들의 주요 사상을 물려받았다.위치 시간 논리학의 연구는 60년대와 70년대에 니콜라스 레셔에 의해 계속되었다.연대논리에 관한 메모(1966), 연대기 명제의 논리에 대하여(1968), 위상논리(1968), 시간논리(1971) 등의 저서에서 그는 우에와 선행의 시스템 사이의 연관성을 연구하였다.게다가 그는 특정 위치 ^[6]논리학에서 실현 연산자를 사용하여 Prior의 시제 연산자를 정의할 수 있다는 것을 증명했다.그의 연구에서 Rescher는 또한 보다 일반적인 위치 논리 시스템을 만들었다.첫 번째 것은 순전히 시간적 사용을 위해 구성되었지만, 그는 실현 연산자를 포함하도록 의도되었지만 시계 공리와 같은 특정한 시간적 공리가 없는 위상 논리 용어를 제안했다.

이항 시간 연산자 Since and Will은 1968년 한스 캄프가 박사 ^[7]논문에서 소개한 것으로, 시간 논리와 1차 논리에 관련된 중요한 결과, 즉 현재 캄프의 ^[8]^[2]^[9]정리로 알려진 결과를 포함하고 있다.

공식 검증의 두 가지 초기 경쟁자는 선형 시간 논리, Amir Pnueli의 선형 시간 논리, Mordechai Ben-Ari, Zohar Manna 및 Amir Pnueli의 분기 시간 논리인 계산 트리 논리였다.CTL과 거의 동등한 형식주의가 E. M . 클라크와 E. A. 에머슨에 의해 비슷한 시기에 제안되었다.두 번째 논리가 첫 번째 논리보다 더 효율적으로 결정될 수 있다는 사실은 때때로 주장되어 온 것처럼 일반적으로 분기 논리 및 선형 논리에는 반영되지 않습니다.오히려, 에머슨과 레이는 어떤 선형 논리도 같은 복잡성으로 결정될 수 있는 분기 논리로 확장될 수 있다는 것을 보여준다.

우에의 위치 논리

1947년 석사논문이 폴란드어로 ^[10]발표되면서 그의 논리가 발표됐다.그의 철학적이고 형식적인 개념은 그의 감독관이 얀 우카시에비치의 제자인 예지 스우페키였기 때문에 리비브 바르샤프 논리학교의 연속이라고 볼 수 있다.비록 Henryk Hi presented가 1951년 Journal of Symbolic Logic에 짧지만 유익한 리뷰를 발표했지만, 이 논문은 1977년까지 영어로 번역되지 않았다.그의 리뷰는 그의 작업에 대한 핵심 개념을 포함했고 논리적인 커뮤니티 사이에서 Wo'의 결과를 널리 알리기에 충분했다.이 작업의 주된 목적은 형식 논리학의 틀에서 밀의 규범을 제시하는 것이었다.이 목표를 달성하기 위해 저자는 밀의 개념 구조에서 시간 함수의 중요성을 연구했다.그것을 가지고 그는 시간적인 측면과 함께 밀의 규범에 맞는 그의 공리적인 논리 체계를 제공했다.

구문

Podstawy Analizy Metodologicalznej Kanonov Milla(밀의 방법의 방법론적 분석 기초)에 처음 발표된 논리의 언어는 다음과 같이 ^[3]구성되었다.

1차 로직 연산자 'syslog', 'syslog', 'syslog', '→', 'syslog', 'syslog' 및 'syslog'
실현 연산자 U
기능 기호 δ
명제 변수₁ p,p₂,p₃,...
시간₁ 모멘트를₂ 나타내는₃ 변수 t, t, t, ...
시간 간격₁ n,n₂,n₃,...을 나타내는 변수

용어 집합(S로 표시)은 다음과 같이 구성됩니다.

시간 모멘트 또는 간격을 나타내는 변수는 용어입니다.
$\tau \in S$ S $\tau \in S$ \ $displaystyle$ \ $tau$ \ $in$ S $\tau \in S$ $\epsilon$ 、 $\delta (\tau ,\epsilon )\in S$ \ $displaystyle$ \ $epsilon ）$ $\delta (\tau ,\epsilon )\in S$ S \ $displaystyle$ \ $delta$ ( \ $tau$ , \ $epsilon )\$ in S 。

공식 세트(For로 표시)는 ^[10]다음과 같이 구성됩니다.

모든 1차 논리식이 유효합니다.
$\tau \in S$ S $\tau \in S$ \ $displaystyle$ \ $tau$ \ $in$ S $\tau \in S$ and $\tau \in S$ $\phi$ $U_{\tau }(\phi )\in For$ $\phi$ $U_{\tau }(\phi )\in For$ \ displaystyle \ $phi }$ $U_{\tau }(\phi )\in For$ $U_{\tau }(\phi )\in For$ $U_{\tau }(\phi )\in For$ r \ $displaystyle U_{$ \ $tau$ } （ \ $phi$ ）\ $in$ For $U_{\tau }(\phi )\in For$
[ $\phi \in For$ r \ $display style$ \ $phi$ \ $\phi \in For$ $For$ ]의 경우 $\neg \phi \in For$ [ F $o$ r \ $displaystyle$ \ $neg$ \ $phi$ \ in For $\neg \phi \in For$ ]의 경우 [ F $\neg \phi \in For$ r \ displaystyle \ neg \ phi \ $in$ For ]
[ $\phi ,\psi \in For$ ], [ $\phi ,\psi \in For$ $r$ \ $displaystyle \phi ],$ [\ $psi \$ For $\circ \in \{\wedge ,\vee ,\rightarrow ,\equiv \}$ 및 $\circ \in \{\wedge ,\vee ,\rightarrow ,\equiv \}$ displaystyle \in \ $vee,\equiv$ \} $\circ \in \{\wedge ,\vee ,\rightarrow ,\equiv \}$ (\ $displaystyle \in \{\vee,\$ equiv $\circ \in \{\wedge ,\vee ,\rightarrow ,\equiv \}$ 의 경우 $[\$ displaystyle $\Phi]$ 는 \ $Displaystyle$ \Phi $\phi \circ \psi \in For$ 에 사용됩니다.
$\phi \in For$ R $\phi \in For$ \ $display \phi \in$ For $\phi \in For$ $Q\in \{\forall ,\exists \}$ qQ $、$ { $display style$ Q \ $in$ \ { \ $forall$ , \ $exists$ \ } and $Q\in \{\forall ,\exists \}$ a,가 명제, 모멘트 또는 인터벌 변수인 $Q_{\upsilon }\phi \in For$ $Q_{\upsilon }\phi \in For$ $o$ F $Q_{\upsilon }\phi \in For$ F 、 \ $displaystyle$ Q _ \ $ilon$ \ ilon \ $ilon$ \ ilon \ $Q_{\upsilon }\phi \in For$ ilon \ $phi 。$

오리지널 액시오토믹 시스템

$U_{t_{1}}\neg p_{1}\equiv \neg U_{t_{1}p_{1}$
${displaystyle U_{1}(p_{1}\rightarrow p_{2})\rightarrow(U_{t_{1}\rightarrow U_{1}\rightarrow U_{t_{1}}p_{2})$
$({displaystyle U_{1}\rightarrow p_{2}\rightarrow (p_{2}\rightarrow p_{3})\rightarrow (p_{1}\rightarrow p_{3})})$
$(\displaystyle U_{1}}(p_{1}\rightarrow(\neg p_{1}\rightarrow p_{2}) )$
$U_{1}}(\neg p_{1}\rightarrow p_{1}\rightarrow p_{1})$
$\displaystyle \forall _{t_{1}U_{t_{1}}p_{1}\rightarrow p_{1}}$
$\displaystyle \forall _{t_{1}}\exists _{t_{2}\forall _{p_{1}(U_{\delta (t_{1}_{1})}p_{1}\equiv U_{t_{2}}p_1})$
$\displaystyle \forall _{t_{1}\forall _{t_{2}\forall _{p_{1}(U_{\delta (t_{2},n_{1})}p_{1}\equiv U_{t_{1})$
$({displaystyle _{t_{1}}\exists _{p_{1}}\forall _{t_{2}){equiv \forall _{p_{1}\equiv \forall _{p_{2})(U_{t_{1}}p_{2}\equiv U_{2}})$

선행시제논리(TL)

시간 및 모달리티에 도입된 센텐셜 시제 로직은 (일차 명제 ^[11]로직의 모든 일반적인 진실 함수 연산자 외에) 4개의 (비진실 함수) 모달 연산자를 가지고 있다.

P: "그건..." (P는 "과거"의 약자)
F : "그럴 경우" (F는 "미래"의 약자)
G: "항상...."
H: "항상 그랬는데..."

θ를 무한 ^[12]패스로 하면, 이것들을 조합할 수 있습니다.

$\pi \vDash FG\phi$ F $\pi \vDash FG\phi$ ${\display$ （ { $displaystyle \pi$ \vDash $FG \phi$ ） : "어느 $시점$ 에서는 경로의 모든 미래 상태에서 $"\displaystyle$ \phi $"$ 가 $\phi$ 입니다 $\phi$ ."
$π$ $\pi \vDash GF\phi$ ${\$ { $displaystyle$ \ $pi$ \ vDash $GF$ \ phi $\pi \vDash GF\phi$ } : $\phi$ " $경로상의$ 무한히 많은 상태에서는 { $displaystyle$ \ phi $\phi$ }가 $\phi$ 참입니다."

P와 F에서 G와 H를 정의할 수 있으며, 그 반대도 마찬가지입니다.

$디스플레이 스타일F&\equiv \lnot G\lnot \P&\equiv \lnot H\lnot \end {aligned}}$

구문 및 의미론

TL 의 최소 구문은, 다음의 BNF 문법으로 지정합니다.

$\displaystyle \phi, \psi ::=a\; \;\bot \;\lnot \phi \;\;\phi \;\phi \;\;\phi \;\;G\phi \;H\phi }$

여기서 a는 원자식입니다.^[13]

크립케 모형은 TL에서 문장의 진실성을 평가하는 데 사용됩니다.한 쌍(T, <) 세트의T및 이진 관계 < onT('인스턴스'라고 불립니다)는 프레임이라고 불립니다.모델은 3배로 부여된다.T, <,V프레임 및 함수의)V각 쌍에 할당하는 밸류에이션(valuation)이라고 한다.a,u)와 시간 값의 true 값을 지정합니다.이 개념은ϕ모델에서 참입니다.U=(T, <,V)이(가 됩니다.u"는 생략형입니다.U⊨ϕ[u] 이 ^[14]표기법에서는


진술	...은 딱 맞는 말이다.
`U`⊨`a`[`u`]	`V`(`a`,`u`= 참
`U`⊨¬`ϕ`[`u`]	것은 아니다.`U`⊨`ϕ`[`u`]
`U`⊨(`ϕ`∧`ψ`)[`u`]	`U`⊨`ϕ`[`u`] 및`U`⊨`ψ`[`u`]
`U`⊨(`ϕ`∨`ψ`)[`u`]	`U`⊨`ϕ`[`u`] 또는`U`⊨`ψ`[`u`]
`U`⊨(`ϕ`→`ψ`)[`u`]	`U`⊨`ψ`[`u`] 만약`U`⊨`ϕ`[`u`]
`U`§ G`ϕ`[`u`]	`U`⊨`ϕ`[`v`] 모두를 위해`v`와 함께`u`< >`v`
`U`hH`ϕ`[`u`]	`U`⊨`ϕ`[`v`] 모두를 위해`v`와 함께`v`< >`u`

소정의 클래스F액자에 있어서 문장ϕ의 TL은

에 관해서 유효한F모든 모델에 대해서U=(T,<,V)와 함께 ( )를 사용합니다.T,<)인F그리고 모든 사람을 위해u에T,U⊨ϕ[u]
에 관해서 만족스러운.F모형이 있으면U=(T,<,V)와 함께 ( )를 사용합니다.T,<)인F어떤 사람에게는 그렇게u에T,U⊨ϕ[u]
문장의 결과ψ에 관하여F모든 모델에 대해서U=(T,<,V)와 함께 ( )를 사용합니다.T,<)인F그리고 모든 사람을 위해u에T,한다면U⊨ψ[u>, 그럼U⊨ϕ[u]

많은 문장은 제한된 프레임 클래스에 대해서만 유효합니다.프레임의 클래스는 일반적으로 전이성, 반대칭성, 반사성, 트리코토믹, 비반사성, 합계, 조밀성 또는 이들의 조합이 있는 것으로 한정됩니다.

최소한의 자명한 논리

Burgess는 <의 관계에 대해 어떠한 가정도 하지 않지만 다음 공리 ^[15]스키마에 기초하여 의미 있는 추론을 가능하게 하는 논리를 개략적으로 설명합니다.

A어디에A1차 논리의 반복이다.
G(A→B→(G)A→GB)
H(A→B→(H)A→HB)
A→GPA
A→ 고주파A

다음과 같은 공제 규칙이 있다.

정해진A→B그리고.A, 추론B(모더스 포넨)
동음이의가 주어지다. A, 유추 GA
동음이의가 주어지다. A, 유추 HA

다음 규칙을 도출할 수 있습니다.

Becker의 규칙: 지정A→B, T를 추론합니다.A→TB여기서 T는 G, H, F, P로 이루어진 시제이다.
미러링: 주어진 정리A, 미러 스테이트먼트를 추론합니다. A이는 G를 H로 치환하고(따라서 F를 P로 치환), 그 반대도 마찬가지입니다^§.
이중성: 주어진 정리A, 이중 스테이트먼트를 추론합니다. A*는 with과 ,, G와 F, H와 P를 교환하여 얻을 수 있습니다.

술어 로직으로의 변환

Burgess는 Meredith에게 TL의 스테이트먼트에서 1차 논리 스테이트먼트로의 번역을 제공한다.x₀ (현재의 순간을 나타냄)이 번역문M는 다음과 ^[16]같이 재귀적으로 정의됩니다.

${\displaystyle{\begin{정렬}&, M(를)&,&=a^{*}x_{0}\\&, M(\lnot \phi)&, &, =\lnot M(\phi)\\&amp을 말한다.M(\phi \land \psi)&,&=M(\phi)\land M(\psi)\\&amp을 말한다.M({\mathsf{G}}\phi)&,&=\forall x_ᆪ(x_{0}일 경우<>x_{1}\rightarrow M(A^{+}))\.\&, M({\mathsf{H}}\phi)&,&=\forall x_ᆪ(x_{1}<>x_{0}일 경우 \rightarrow M(A^{+}))\end{정렬}}}.$

$A^{+}$ 서 $A^{+}$ A $A^{+}$ + {\ $displaystyle$ A $^{+}$ 는 $A^{+}$ 모든 변수 인덱스가 1씩 증가하는 $문장$ A(\ $displaystyle$ A $^{*})$ 이고 $A$ $,$ A(\ $displaystyle$ a^{*})는 $a^{*}$ x $x\mapsto V(a,x)$ V $(a,x$ 로 정의된1 자리수의 술어입니다.

시간 연산자

시간 논리에는 논리 연산자와 모달 ^[17]연산자의 두 가지 연산자가 있습니다.논리연산자는 통상의 진실함수 연산자( 「 $\neg ,\lor ,\land ,\rightarrow$ , 「 $\neg ,\lor ,\land ,\rightarrow$ , $→$ { $displaystyle \neg$ , \ $lor$ , \ $land$ , \ $rightarrow }$ )입니다.선형 시간 논리 및 계산 트리 로직에서 사용되는 모달 연산자는 다음과 같이 정의됩니다.

텍스트	심볼릭	정의.	설명.
이진 연산자
$φ$ U $ψ$	$\displaystyle \phi ~{\mathcal {U}}~\psi }$	$\displaystyle (B,{\mathcal {U}},C) (\phi)=\ (\cisco i:C(\phi _{i})\land (\forall j <i:B(\phi _{j})}$	holds까지 : $holds$ 는 현재 또는 미래 위치에 유지되고 $has$ 는 그 위치까지 유지되어야 합니다.그 위치에서는 더 이상 $does$ 을 유지할 필요가 없다.
$φ$ R $ψ$	$\displaystyle \phi ~{\mathcal {R}}~\psi }$	$\displaystyle(B,{\mathcal {R}},C)\(\phi)=\(\forall i:C(\phi _{i})\lor(\lor j<i:B(\phi _{j})}$	Release: " $가$ true인 경우 " 가 true인 첫 번째 위치(또는 그러한 위치가 존재하지 않는 경우 영속적)까지를 $해방$ 합니다.
단항 연산자
N $φ$	$\displaystyle \bigcirc \phi }$	${N}B(\phi _{i})=B(\phi _{i+1})$	다음: $①은$ 다음 상태로 유지되어야 합니다.(X는 동의어로 사용됩니다.)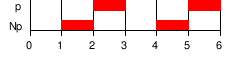
F $φ$	$\displaystyle \Diamond \phi }$	${F}B(\phi)=(참, {\mathcal {U}},B)(\phi)$	Future:는 최종적으로 보류해야 합니다(후행 경로상의 어딘가에서).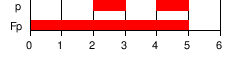
G $φ$	$\displaystyle \Box \phi }$	${G}B(\phi)=\neg {\mathcal {F}\neg B(\phi)$	글로벌하게:는 후속 경로 전체를 유지해야 합니다.
A $φ$	$\displaystyle \forall \phi }$	$(\displaystyle({\mathcal {A}}B})=\ (\forall \phi :\phi _{0}=\psi \to B(\phi))) ) )$	All: 는 현재 상태에서 $시작$ 하는 모든 경로에서 보류해야 합니다.
E $φ$	$\displaystyle \phi }$	$(\displaystyle({\mathcal {E}}B})=\(\phi :\phi _{0}=\psi \land B(\phi ))) ),$	존재: " 가 $유지$ 되는 현재 상태에서 시작하는 경로가 하나 이상 존재합니다.

대체 기호:

연산자 R은 때때로 V로 표시된다.
연산자 W는 연산자가 될 때까지 약합니다. $f\mathbf {W} g$ $f\mathbf {W} g$ g {\ $displaystyle$ $f$ \ $mathbf {W} g$ }은 $f\mathbf {W} g$ $f\mathbf {U} g\lor \mathbf {G} f$ $f\mathbf {U} g\lor \mathbf {G} f$ † $f\mathbf {U} g\lor \mathbf {G} f$ f {\ $display$ f\ $mathbf {U}$ g\ $lor \mathbf {G}$ f}에 해당합니다.

단항 연산자는 B $() φ$ 의 형식이 적절할 $때$ 마다 올바른 공식입니다.바이너리 $연산자$ 는 B $() φ$ 와 C $() φ$ 의 형식이 적절할 $때$ 마다 올바른 공식입니다.

일부 논리에서는 일부 연산자를 표현할 수 없습니다.예를 들어, N 연산자는 동작의 시간 논리에서는 표현할 수 없습니다.

시간 논리

시간 논리에는 다음이 포함됩니다.

일부 위치 논리 시스템
Interval Temporal Logic(ITL)
LTL(Linear Temporal Logic)
계산 트리 로직(CTL)
신호 시간 논리(STL)^[18]
타임스탬프 시간 논리(TTL)^[19]
속성 사양 언어(PSL)
LTL 및 CTL을 일반화하는 CTL*
헤네시-밀너 논리(HML)
HML 및 CTL* 서브셋으로 포함하는 모달μ-calculus
MTL(^[20]Metric Temporal Logic)
Metric Interval Temporal Logic(MITL;^[18] 메트릭 간격 시간 논리)
Time Proposition Temporal Logic(TPTL; 시간 명제 시간 논리)
TLTL(^[21]Truncated Linear Temporal Logic)
하이퍼 시간 논리(Hyper)LTL) ^[22]

시간, 연대, 시제 로직과 밀접하게 관련된 변이는 "위상", "장소" 또는 "공간 위치"^[23]^[24]에 기반한 모달 로직입니다.

「」를 참조해 주세요.

메모들

^ Vardi 2008, 페이지 153
^ ^a ^b ^c Vardi 2008, 페이지 154
^ ^a ^b Łoś, Jerzy (1920-1998); Łoś, Jerzy (1920-1998) (1947). Podstawy analizy metodologicznej kanonów Milla. nakł. Uniwersytetu Marii Curie-Skłodowskiej.
^ ^a ^b ^c ^d Øhrstrøm, Peter (2019). "The Significance of the Contributions of A.N.Prior and Jerzy Łoś in the Early History of Modern Temporal Logic". Logic and Philosophy of Time: Further Themes from Prior, Volume 2.
^ Peter Øhrstrøm; Per F. V. Hasle (1995). Temporal logic: from ancient ideas to artificial intelligence. Springer. ISBN 978-0-7923-3586-3. 페이지 176–196, 210
^ ^a ^b Rescher, Nicholas; Garson, James (January 1969). "Topological Logic". The Journal of Symbolic Logic. 33 (4): 537–548. doi:10.2307/2271360. ISSN 0022-4812.
^ "Temporal Logic (Stanford Encyclopedia of Philosophy)". Plato.stanford.edu. Retrieved 2014-07-30.
^ Walter Carnielli; Claudio Pizzi (2008). Modalities and Multimodalities. Springer. p. 181. ISBN 978-1-4020-8589-5.
^ Sergio Tessaris; Enrico Franconi; Thomas Eiter (2009). Reasoning Web. Semantic Technologies for Information Systems: 5th International Summer School 2009, Brixen-Bressanone, Italy, August 30 – September 4, 2009, Tutorial Lectures. Springer. p. 112. ISBN 978-3-642-03753-5.
^ ^a ^b Tkaczyk, Marcin; Jarmużek, Tomasz (2019). "Jerzy Łoś Positional Calculus and the Origin of Temporal Logic". Logic and Logical Philosophy. 28 (2): 259–276. doi:10.12775/LLP.2018.013. ISSN 2300-9802.
^ Prior, Arthur Norman (2003). Time and modality: the John Locke lectures for 1955–6, delivered at the University of Oxford. Oxford: The Clarendon Press. ISBN 9780198241584. OCLC 905630146.
^ Lawford, M. (2004). "An Introduction to Temporal Logics" (PDF). Department of Computer Science McMaster University.
^ Goranko, Valentin; Galton, Antony (2015). Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (Winter 2015 ed.). Metaphysics Research Lab, Stanford University.
^ Müller, Thomas (2011). "Tense or temporal logic" (PDF). In Horsten, Leon (ed.). The continuum companion to philosophical logic. A&C Black. p. 329.
^ Burgess, John P. (2009). Philosophical logic. Princeton, New Jersey: Princeton University Press. p. 21. ISBN 9781400830497. OCLC 777375659.
^ Burgess, John P. (2009). Philosophical logic. Princeton, New Jersey: Princeton University Press. p. 17. ISBN 9781400830497. OCLC 777375659.
^ "Temporal Logic". Stanford Encyclopedia of Philosophy. February 7, 2020. Retrieved April 19, 2022.
^ ^a ^b 말러, O.; 니코비치, D. (2004)"연속 신호의 시간적 특성 모니터링". doi:10.1007/978-3-540-30206-3_12.
^ Mehrabian, Mohammadreza; Khayatian, Mohammad; Shrivastava, Aviral; Eidson, John C.; Derler, Patricia; Andrade, Hugo A.; Li-Baboud, Ya-Shian; Griffor, Edward; Weiss, Marc; Stanton, Kevin (2017). "Timestamp Temporal Logic (TTL) for Testing the Timing of Cyber-Physical Systems". ACM Transactions on Embedded Computing Systems. 16 (5s): 1–20. doi:10.1145/3126510. S2CID 3570088.
^ 코이만스, R. (1990년)"메트릭 시간 로직으로 실시간 속성 지정", 실시간 시스템 2(4): 255–299. doi: 10.1007/BF01995674.
^ 리, 샤오, 크리스티안-이오안 바실레, 칼린 벨타."시간적 논리 보상을 통한 강화 학습." doi :10.1109/IROS.2017.8206234
^ Clarkson, Michael R.; Finkbeiner, Bernd; Koleini, Masoud; Micinski, Kristopher K.; Rabe, Markus N.; Sánchez, César (2014). "Temporal Logics for Hyperproperties". Principles of Security and Trust. Lecture Notes in Computer Science. Vol. 8414. pp. 265–284. doi:10.1007/978-3-642-54792-8_15. ISBN 978-3-642-54791-1. S2CID 8938993.
^ Rescher, Nicholas (1968). "Topological Logic". Topics in Philosophical Logic. pp. 229–249. doi:10.1007/978-94-017-3546-9_13. ISBN 978-90-481-8331-9.
^ von Wright, Georg Henrik (1979). "A Modal Logic of Place". The Philosophy of Nicholas Rescher. pp. 65–73. doi:10.1007/978-94-009-9407-2_9. ISBN 978-94-009-9409-6.

레퍼런스

모르드카이 벤아리, 조하르 마나, 아미르 피뉴엘리:분기시간의 시간논리 POPL 1981: 164~176
Amir Pnueli:프로그램의 시간 논리 FOCS 1977: 46~57
Venema, Yde, 2001, "Temporal Logic", 루, 고블, ed., The Blackwell Guide to Philosical Logic.블랙웰이요
E. A. Emerson과 C.레이, "모델 확인을 위한 양식: 분기 시간 로직 역습", 컴퓨터 프로그래밍 과학 8, 페이지 275–306, 1987.
E. A. Emerson, "시간적 및 모달 논리", 이론 컴퓨터 과학 핸드북, 16장, MIT Press, 1990
PSL 실무 입문, Cindy Eisner, Dana Fisman
Vardi, Moshe Y. (2008). "From Church and Prior to PSL". In Orna Grumberg; Helmut Veith (eds.). 25 years of model checking: history, achievements, perspectives. Springer. ISBN 978-3-540-69849-4. 프리프린트 합니다.컴퓨터 공학과 공학에서 이질적으로 보이는 아이디어가 어떻게 모였는지에 대한 역사적 관점. (이 논문 제목에서 처치에 대한 언급은 처치가 하드웨어 검증을 수행하는 방법을 제안한 1957년의 거의 알려지지 않은 논문을 참조한 것입니다.)

추가 정보

Peter Øhrstrøm; Per F. V. Hasle (1995). Temporal logic: from ancient ideas to artificial intelligence. Springer. ISBN 978-0-7923-3586-3.

외부 링크

스탠포드 철학 백과사전: Anthony Galton의 "Temporal Logic".
Yde Venema의 Temporal Logic, 구문과 의미론의 형식적 설명, 공리화 질문.또한 Camp의 2차 시간 연산자 처리(이후,까지)
Ian Hodkinson의 시간 논리 게임에 대한 메모(일차 시간 논리 공식 설명 포함)
CADP – 다양한 시간 로직을 위한 범용 모델 체커를 제공합니다.
PAT는 CSP 및 그 확장(공유 변수, 어레이, 광범위한 공정성을 갖춘)을 위한 강력한 무료 모델 검사기, LTL 검사기, 시뮬레이터 및 미세 검사기입니다.

[1] Vardi 2008, 페이지 153

[v154-2] Vardi 2008, 페이지 154

[:0-3] Łoś, Jerzy (1920-1998); Łoś, Jerzy (1920-1998) (1947). Podstawy analizy metodologicznej kanonów Milla. nakł. Uniwersytetu Marii Curie-Skłodowskiej.

[:1-4] Øhrstrøm, Peter (2019). "The Significance of the Contributions of A.N.Prior and Jerzy Łoś in the Early History of Modern Temporal Logic". Logic and Philosophy of Time: Further Themes from Prior, Volume 2.

[5] Peter Øhrstrøm; Per F. V. Hasle (1995). Temporal logic: from ancient ideas to artificial intelligence. Springer. ISBN 978-0-7923-3586-3. 페이지 176–196, 210

[:2-6] Rescher, Nicholas; Garson, James (January 1969). "Topological Logic". The Journal of Symbolic Logic. 33 (4): 537–548. doi:10.2307/2271360. ISSN 0022-4812.

[7] "Temporal Logic (Stanford Encyclopedia of Philosophy)". Plato.stanford.edu. Retrieved 2014-07-30.

[CarnielliPizzi2008-8] Walter Carnielli; Claudio Pizzi (2008). Modalities and Multimodalities. Springer. p. 181. ISBN 978-1-4020-8589-5.

[TessarisFranconi2009-9] Sergio Tessaris; Enrico Franconi; Thomas Eiter (2009). Reasoning Web. Semantic Technologies for Information Systems: 5th International Summer School 2009, Brixen-Bressanone, Italy, August 30 – September 4, 2009, Tutorial Lectures. Springer. p. 112. ISBN 978-3-642-03753-5.

[Tkaczyk_2019_259–276-10] Tkaczyk, Marcin; Jarmużek, Tomasz (2019). "Jerzy Łoś Positional Calculus and the Origin of Temporal Logic". Logic and Logical Philosophy. 28 (2): 259–276. doi:10.12775/LLP.2018.013. ISSN 2300-9802.

[11] Prior, Arthur Norman (2003). Time and modality: the John Locke lectures for 1955–6, delivered at the University of Oxford. Oxford: The Clarendon Press. ISBN 9780198241584. OCLC 905630146.

[12] Lawford, M. (2004). "An Introduction to Temporal Logics" (PDF). Department of Computer Science McMaster University.

[13] Goranko, Valentin; Galton, Antony (2015). Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (Winter 2015 ed.). Metaphysics Research Lab, Stanford University.

[14] Müller, Thomas (2011). "Tense or temporal logic" (PDF). In Horsten, Leon (ed.). The continuum companion to philosophical logic. A&C Black. p. 329.

[15] Burgess, John P. (2009). Philosophical logic. Princeton, New Jersey: Princeton University Press. p. 21. ISBN 9781400830497. OCLC 777375659.

[16] Burgess, John P. (2009). Philosophical logic. Princeton, New Jersey: Princeton University Press. p. 17. ISBN 9781400830497. OCLC 777375659.

[17] "Temporal Logic". Stanford Encyclopedia of Philosophy. February 7, 2020. Retrieved April 19, 2022.

[autogenerated2004-18] 말러, O.; 니코비치, D. (2004)"연속 신호의 시간적 특성 모니터링". doi:10.1007/978-3-540-30206-3_12.

[19] Mehrabian, Mohammadreza; Khayatian, Mohammad; Shrivastava, Aviral; Eidson, John C.; Derler, Patricia; Andrade, Hugo A.; Li-Baboud, Ya-Shian; Griffor, Edward; Weiss, Marc; Stanton, Kevin (2017). "Timestamp Temporal Logic (TTL) for Testing the Timing of Cyber-Physical Systems". ACM Transactions on Embedded Computing Systems. 16 (5s): 1–20. doi:10.1145/3126510. S2CID 3570088.

[20] 코이만스, R. (1990년)"메트릭 시간 로직으로 실시간 속성 지정", 실시간 시스템 2(4): 255–299. doi: 10.1007/BF01995674.

[21] 리, 샤오, 크리스티안-이오안 바실레, 칼린 벨타."시간적 논리 보상을 통한 강화 학습." doi :10.1109/IROS.2017.8206234

[22] Clarkson, Michael R.; Finkbeiner, Bernd; Koleini, Masoud; Micinski, Kristopher K.; Rabe, Markus N.; Sánchez, César (2014). "Temporal Logics for Hyperproperties". Principles of Security and Trust. Lecture Notes in Computer Science. Vol. 8414. pp. 265–284. doi:10.1007/978-3-642-54792-8_15. ISBN 978-3-642-54791-1. S2CID 8938993.

[23] Rescher, Nicholas (1968). "Topological Logic". Topics in Philosophical Logic. pp. 229–249. doi:10.1007/978-94-017-3546-9_13. ISBN 978-90-481-8331-9.

[24] von Wright, Georg Henrik (1979). "A Modal Logic of Place". The Philosophy of Nicholas Rescher. pp. 65–73. doi:10.1007/978-94-009-9407-2_9. ISBN 978-94-009-9409-6.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

v t 비고전적 논리
직관주의	직관적 논리 건설적 분석 헤이팅 산수 직관적 유형 이론 구성 집합론
흐릿하다	진실의 정도 퍼지 규칙 퍼지 집합 퍼지 유한 요소 퍼지 집합 작업
하부 구조	구조 규칙 관련성 논리 선형 논리
파라콘존재	디알테히즘
묘사	온톨로지 온톨로지 언어
다치	3치 4값 우카시에비치
디지털 로직	삼국논리 트라이스테이트 버퍼 4값 베릴로그 IEEE 1164 VHDL
다른이들	동적 의미론 호기심 논리 중간 논리 비단조 논리

Search

시간 논리

네임스페이스

더

목차

동기

역사

우에의 위치 논리