유동소성 이론

얇은 금속 시트의 소성 변형.

유동소성(flow pasticity)은 고체역학 이론으로 물질의 플라스틱 행동을 기술하는 데 사용된다.^[1]유동 가소성 이론은 물질의 소성 변형량을 결정하는 데 사용할 수 있는 흐름 규칙이 존재한다고 가정하는 것이 특징이다.

유동 가소성 이론에서, 신체의 총 변종은 탄성 부분과 플라스틱 부분으로 추가적으로 분해될 수 있다고 가정한다.스트레인의 탄성 부분은 선형 탄성 또는 과대 재생성 구성 모델에서 계산할 수 있다.그러나 변형률의 플라스틱 부분을 결정하려면 흐름 규칙과 강화 모델이 필요하다.

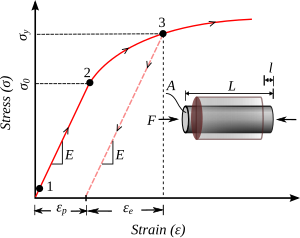
소변형 이론

단일 축압에서 재료의 대표적인 플라스틱 동작을 보여주는 응력 변형 곡선.변종은 회수가능탄성변형(

\varepsilon _{e}

e

\varepsilon _{e}

{\

displaystyle \varepsilon _{e

과 비탄성변형변형(

\varepsilon _{p}

\varepsilon _{p}

{\

으로 분해할 수 있다.

\varepsilon _{p}

초기 항복시 응력은

\sigma _{0}

{\

변형경화재의 경우(그림과 같이)

\sigma _{y}

y

{\

값으로 변형이 증가함에 따라 항복응력이 증가한다

\sigma _{y}

단방향 하중을 위한 대표적인 유동 가소성 이론(소형변형 완벽한 가소성 또는 강화 가소성)은 다음 요건에 기초하여 개발된다.

그 물질은 선형 탄성 범위를 가지고 있다.
소재는 플라스틱 변형이 처음 발생하는 응력으로 정의되는 탄성 한계, 즉 $\sigma =\sigma _{0}$ = $\sigma =\sigma _{0}$ $\sigma =\sigma _{0}$ ${\$
탄성 한계를 벗어나면 응력 상태는 항상 항복 표면에 남아 있다. 즉, $\sigma =\sigma _{y}$ = $\sigma =\sigma _{y}$ $\sigma =\sigma _{y}$ ${\$
하중은 응력 증가가 0보다 큰 상황, 즉 $d\sigma >0$ $d\sigma >0$ > $d\sigma >0$ ${\displaystyle d\sigma >0$ 하중이 응력 상태를 플라스틱 영역으로 가져가는 경우 플라스틱 변형률 증가는 항상 0, $d\varepsilon _{p}>0$ d $d\varepsilon _{p}>0$ p > $d\varepsilon _{p}>0$ ${\displaystyle d\varepsilon _{p}0$ 보다 커진다.
언로딩은 스트레스의 증분이 0보다 작은 상황으로 정의된다. $d\sigma <0$ , d $d\sigma <0$ < $d\sigma <0$ [\ $displaystyle d$ \sigma $<0$ 하역 시 소재는 탄성이 좋아 플라스틱 변형량이 추가로 쌓이지 않는다.
총 변형률(total strain $d\varepsilon =d\varepsilon _{e}+d\varepsilon _{p}$ 은 탄성 부분과 플라스틱 부분의 선형 결합이다. 즉, $d\varepsilon =d\varepsilon _{e}+d\varepsilon _{p}$ $d\varepsilon =d\varepsilon _{e}+d\varepsilon _{p}$ = $d\varepsilon =d\varepsilon _{e}+d\varepsilon _{p}$ $d\varepsilon =d\varepsilon _{e}+d\varepsilon _{p}$ e + $d\varepsilon =d\varepsilon _{e}+d\varepsilon _{p}$ $d\varepsilon =d\varepsilon _{e}+d\varepsilon _{p}$ p ${\$ d $\varepsilon$ = $d\varepsilon _{e}+d\varepsilon _{p$ 플라스틱 부품은 탄성 부품이 완전히 복구될 수 있는 동안에는 회수할 수 없다.
하중-언로드 사이클의 작업은 양수 또는 0, $d\sigma \,d\varepsilon =d\sigma \,(d\varepsilon _{e}+d\varepsilon _{p})\geq 0$ $d\sigma \,d\varepsilon =d\sigma \,(d\varepsilon _{e}+d\varepsilon _{p})\geq 0$ $d\sigma \,d\varepsilon =d\sigma \,(d\varepsilon _{e}+d\varepsilon _{p})\geq 0$ $d\sigma \,d\varepsilon =d\sigma \,(d\varepsilon _{e}+d\varepsilon _{p})\geq 0$ $d\sigma \,d\varepsilon =d\sigma \,(d\varepsilon _{e}+d\varepsilon _{p})\geq 0$ = $d\sigma \,d\varepsilon =d\sigma \,(d\varepsilon _{e}+d\varepsilon _{p})\geq 0$ $d\sigma \,d\varepsilon =d\sigma \,(d\varepsilon _{e}+d\varepsilon _{p})\geq 0$ ( $d\sigma \,d\varepsilon =d\sigma \,(d\varepsilon _{e}+d\varepsilon _{p})\geq 0$ $d\sigma \,d\varepsilon =d\sigma \,(d\varepsilon _{e}+d\varepsilon _{p})\geq 0$ e + $d\sigma \,d\varepsilon =d\sigma \,(d\varepsilon _{e}+d\varepsilon _{p})\geq 0$ $d\sigma \,d\varepsilon =d\sigma \,(d\varepsilon _{e}+d\varepsilon _{p})\geq 0$ p ) $d\sigma \,d\varepsilon =d\sigma \,(d\varepsilon _{e}+d\varepsilon _{p})\geq 0$ 0 ${\d\paystyle d\sigma$ \,d\barepsilon $\d\sigma \,$ ( $d\varepsilon _{e}+\p}\beq 0$ 이것을 Drucker 안정이라고 부르기도 하며 변형 연화 작용의 가능성을 제거한다.

위의 요건은 다음과 같이 응력과 다방향 하중의 3차원 상태로 표현할 수 있다.

탄력성(후크의 법칙).선형 탄성체에서 재료의 응력과 균주는 다음과 같다.

{\boldsymbol {\sigma}={\mathsf{D}}\\boldsymbol {\barepsilon}}}

여기서 강성

{\mathsf {D}}

D

{\

{\

mathsf{D}}

은

{\mathsf {D}}

(는) 일정하다.

탄성 한계(수율 표면).탄성 한계는 플라스틱 변형에 의존하지 않고 형태를 갖는 항복 표면으로 정의된다.

f({\boldsymbol {\\sigma }=0\,.

탄성 한계를 넘어서.변형 경화 재료의 경우, 항복 표면은 플라스틱 변형률 증가와 함께 진화하며 탄성 한계가 변화한다.진화하는 항복 표면은 형태를 가지고 있다.

f({\boldsymbol {\\sigma }},{\\boldsymbol {\varepsilon }}}}=0\,.

로드 중.일반적인 응력 상태의 경우, 응력 상태가 항복 표면에 있고 응력 증가가 항복 표면의 바깥쪽을 향하면 플라스틱 하중이 표시된다. 이는 응력 증가의 내부 산물 및 항복 표면의 바깥쪽 정규가 양성이면 발생한다.

d{\\jeq 0\,}}Mas\\frac {\based f}{\\based symbol {\basedma }}

위의 방정식은 0과 같을 때 응력 상태가 항복 표면을 따라 이동하는 중립 하중의 상태를 나타낸다.

언로딩: $f<0$ 한 논거가 f $f<0$ < $f<0$ ${\displaystyle f<0$ 소재가 탄성 영역에 있는 경우에 대해 언로딩에 대해 이루어진다.

d{\boardsymbol{\boardf}{\boardsymbol{\boardf}{\boardsymbol{\boardsma}}}}}}<0\,

변형률 분해:균주의 탄성 및 플라스틱 부품으로의 첨가된 분해는 다음과 같이 쓰여질 수 있다.

d{\\symbol {\barepsilon }}=d{\\\\symbol{e}}}+d{\barembol {\varepsilon }\,

안정성 추정:안정성은 다음과 같이 표현된다.

d{\\bmbol {\bma}:d{\bmbol {\barepsilon}}}\geq 0\,.

흐름 규칙

금속 가소성에서는 플라스틱 변형률 증가와 일차 응력 텐서가 동일한 주요 방향을 가지고 있다는 가정은 흐름 규칙이라는 관계에서 캡슐화된다.암석 가소성 이론도 수율 표면의 압력에 의존하는 요건이 위의 가정을 완화시킬 필요가 있다는 점을 제외하고는 유사한 개념을 사용한다.대신, 일반적으로 플라스틱 변형률 증가와 압력에 의존하는 항복 표면에 대한 정규 분포가 같은 방향을 갖는다고 가정한다.

d{\basymbol {\barepsilon }}}{p}=d\ba \da \,{\frac {\basymbol {\basma }}}}

여기서 $d\lambda >0$ $d\lambda >0$ > $d\lambda >0$ $d\putda >0$ 은 $d\lambda > 0$ 강화 매개 변수다.이러한 흐름 규칙의 형식을 관련 흐름 규칙이라고 하며, 공동 방향성에 대한 가정을 정규성 조건이라고 한다. $f$ $f$ 기능을 플라스틱 전위라고도 한다 $f$ .

위의 흐름 규칙은 d $d{\boldsymbol {\sigma }}=0$ = 0 ${\displaystyle$ d ${\boldsymbol {\sigma }}d$ $d{\boldsymbol {\varepsilon }}_{p}>0$ $d{\boldsymbol {\varepsilon }}_{p}>0$ > 0 ${\displaystyle$ d ${\boldsymbol {\$ baldsymbol ${\valdsymbol$ 즉 $증가$ 하는 플라스틱 변형 하에서 항복 표면이 일정하게 유지되는 완전 변형에 대해 쉽게 정당화된다.이는 탄성 스트레인의 증가도 후크의 법칙 때문에 0, $d{\boldsymbol {\varepsilon }}_{e}=0$ $d{\boldsymbol {\varepsilon }}_{e}=0$ e $d{\boldsymbol {\varepsilon }}_{e}=0$ = $d{\boldsymbol {\varepsilon }}_{e}=0$ $d{\boldsymbol {\valdsymbol{}_{e}=0$ 임을 의미한다 $d{\boldsymbol {\varepsilon }}_{e}=0$ 그러므로

d{\basymbol{\p}}}\frac {\basedf}{\basymbol {\text{and}}}}}}}}}}=0\\basymbol {\basymbol{\varembol{\p},0\}}}}}

따라서 항복 표면의 정상과 플라스틱 변형률 텐서 모두 응력 텐서와 직각이며 방향이 같아야 한다.

작업 경화 재료의 경우, 수율 표면은 응력이 증가함에 따라 확장될 수 있다.우리는 Drucker의 두 번째 안정성이 극소수의 스트레스 주기에 대해 이 플라스틱 작업이 양성이라는 것을 나타내는 것으로 가정한다.

d{\bmbol {\bma }:d{\bmbol {\varepsilon }}}{p}\geq 0\,

위의 수량은 순전히 탄성 사이클의 경우 0과 같다.플라스틱 적재 해제 사이클에 걸쳐 수행된 작업의 검사를 사용하여 관련 흐름 규칙의 유효성을 정당화할 수 있다.^[2]

일관성 조건

Prager 일관성 조건은 구성 방정식 집합을 닫고 등식 시스템에서 알려지지 $d\lambda$ 않은 매개변수 d $d\lambda$ $d\lambda$ 을(를) 제거하기 위해 필요하다. $df=0$ 조건은 $f({\boldsymbol {\sigma }},{\boldsymbol {\varepsilon }}_{p})=0$ $f({\boldsymbol {\sigma }},{\boldsymbol {\varepsilon }}_{p})=0$ , $f({\boldsymbol {\sigma }},{\boldsymbol {\varepsilon }}_{p})=0$ p $f({\boldsymbol {\sigma }},{\boldsymbol {\varepsilon }}_{p})=0$ ) $f({\boldsymbol {\sigma }},{\boldsymbol {\varepsilon }}_{p})=0$ = $f({\boldsymbol {\sigma }},{\boldsymbol {\varepsilon }}_{p})=0$ ${\displaystyle f({\boldsymbol {\sigma }},{\boldsymbol$ {\baldsymbol ${\varipsilon}}}=0$ 이기 때문에 d $df=0$ = $df=0$ ${\displaystyled=0}$ 이라고 $df = 0$ 명시한다.

df={\frac {\partial f}{\partial {\boldsymbol {\sigma }}}}:d{\boldsymbol {\sigma }}+{\frac {\partial f}{\partial {\boldsymbol {\varepsilon }}_{p}}}:d{\boldsymbol {\varepsilon }}_{p}=0\,.

대변형 이론

가소성의 큰 변형 흐름 이론은 일반적으로 다음 가정 중 하나로 시작한다.

변형 텐서 속도는 탄성 부분과 플라스틱 부분으로 추가적으로 분해될 수 있다.
변형 구배 텐서는 탄성 부분과 플라스틱 부분에서 승법적으로 분해될 수 있다.

첫 번째 가정은 금속의 수치 시뮬레이션에 널리 사용되었으나 점차 승법 이론으로 대체되었다.

승소성소성 운동학

변형 구배를 탄성 및 플라스틱 부품으로 승화 분해하는 개념은 B에 의해 먼저 독립적으로 제안되었다. A. 빌비,^[3] E. 크뢰너,^[4] 수정 가소성의 맥락에서 에라스무스 리에 의해 연속 가소성으로 확장되었다.^[5]분해는 총 변형 구배(F)가 다음과 같이 분해될 수 있다고 가정한다.

{\boldsymbol{F}={\boldsymbol{F}^{F}}\cdot {\boldsymbol{F}^{p}}}}}

여기서 F는^e 탄성(복구 가능) 부분이고 F는^p 변형의 플라스틱(복구 불가능) 부분이다.공간 속도 구배는 다음과 같다.

{\begin{aligned}{\boldsymbol {l}}&={\dot {\boldsymbol {F}}}\cdot {\boldsymbol {F}}^{-1}=\left({\dot {\boldsymbol {F}}}^{e}\cdot {\boldsymbol {F}}^{p}+{\boldsymbol {F}}^{e}\cdot {\dot {\boldsymbol {F}}}^{p}\right)\cdot \left[({\boldsymbol {F}}^{p})^{-1}\cdot ({\boldsymbol {F}}^{e})^{-1}\right]\\&={\dot {\boldsymbol {F}}}^{e}\cdot ({\boldsymbol {F}}^{e})^{-1}+{\boldsymbol {F}}^{e}\cdot [{\dot {\boldsymbol {F}}}^{p}\cdot ({\boldsymbol {F}}^{p})^{-1}]\cdot ({\boldsymbol {F}}^{e})^{-1}\,.\end{정렬}}

여기서 초점(superposed dot)은 시간 분산을 나타낸다.위와 같이 쓸 수 있다.

{\displaystyle{\boldsymbol{l}}={\boldsymbol{{l}^{f}+{\boldsymbol {F}}}\cdot({\boldsymbol{p}}}}}{e}}},{-1},},.}

수량

{\displaystyle {\boldsymbol {L}^{p}:={\dot{\boldsymbol{F}}^{p}}^{p}\cdot ({\boldsymbol{F}^{p}^{1}^{-1})

플라스틱 속도 구배라고 불리며 중간(강력) 무응력 구성으로 정의된다.L의^p 대칭 부분(D^p)은 변형의 소성률이라고 하고, 스큐 대칭 부분(W^p)은 소성 스핀이라고 한다.

{\boldsymbol {D}^{p}={\tfrac {1}{1}{{\boldsymbol{L}}+({\boldsymbol {L}^{p})^{T}]~,~{\boldsymbol{W}^{p}={\tfrac {1}{1}{1}:{2}}[{\boldsymbol{L}-({\boldsymbol {L}^{p})^{\boldsymbol {L}^{p}^{p}}^}^{T}]\,.

일반적으로 플라스틱 스핀은 유한 플라스틱성에 대한 대부분의 설명에서 무시된다.

탄성계통

유한 변형률 체계의 탄성 거동은 일반적으로 과대성 물질 모델에 의해 설명된다.탄성 스트레인은 다음과 같이 정의된 탄성 우측 Cauchy-Green 변형 텐서를 사용하여 측정할 수 있다.

{\boldsymbol {C}^{e}=({\boldsymbol {F}^{e})^{T}\cdot {\boldsymbol {F}^{e}\,

로그 또는 Hency 변형률 텐서는 다음과 같이 정의될 수 있다.

{\boldsymbol {E}^{e:={\tfrac{1}{2}}\ln {\boldsymbol{C}^{e}\,

대칭 만델 응력 텐서는 유한 가소성에 대한 편리한 응력 측정치로 다음과 같이 정의된다.

{\boldsymbol {M}:={\tfrac {1}{1}:{e}\cdot {\boldsymbol {S}+{\boldsymbol {S}+{\boldsymbol {S}\boldsymbol {C}^{e}}}}

여기서 S는 두 번째 Piola-Kirchhoff 스트레스다.로그 변종 측면에서 가능한 과대역학 모델은 다음과 같다.

{\boldsymbol {M}={\frac {\partial W}{\partial {\boldsymbol{E}}}^{E}}}}}=J\,{\frac {dU}}+2\mu \\\\\\cext{\voldsymbol{E}}}}}}}}}}}}}

여기서 W는 변형 에너지 밀도 함수, J = det(F), μ는 계량형이며, "dev"는 텐서의 편차형 부분을 나타낸다.

흐름 규칙

Closius-Duhem 불평등 적용은 플라스틱 스핀이 없는 경우 유한한 변형률 흐름 규칙으로 유도한다.

{\boldsymbol{D}^{p}={\dot {\lambda }\,{\frac {\partial f}{\partial {\boldsymbol{M}}}\,

로드 언로드 조건

하중 언로드 조건은 Karush-Kuhn-Tucker 조건과 동등한 것으로 보일 수 있다.

{\dottyle {\dot}\\geq 0~~f\leq 0~~{\dot{\\\}\,f=0\,}

일관성 조건

일관성 조건은 작은 변형률 케이스의 그것과 동일하다.

{\dottyle {\dot {\potda }\,{\dot {f}=0\,.}

참조

^ Lubliner, Jacob (2008), Plasticity Theory, Courier Dover Publications.
^ 아난다라자(2010년).
^ Bilby, B. A.; Bullough, R.; Smith, E. (1955), "Continuous distributions of dislocations: a new application of the methods of non-Riemannian geometry", Proceedings of the Royal Society A, 231 (1185): 263–273, Bibcode:1955RSPSA.231..263B, doi:10.1098/rspa.1955.0171
^ Kröner, E. (1958), "Kontinuumstheorie der Versetzungen und Eigenspannungen", Erg. Angew. Math., 5: 1–179
^ Lee, E. H. (1969), "Elastic-Plastic Deformation at Finite Strains" (PDF), Journal of Applied Mechanics, 36 (1): 1–6, Bibcode:1969JAM....36....1L, doi:10.1115/1.3564580^{[영구적 데드링크]}
^ Anand, L. (1979), "On H. Hencky's approximate strain-energy function for moderate deformations", Journal of Applied Mechanics, 46 (1): 78–82, Bibcode:1979JAM....46...78A, doi:10.1115/1.3424532

참고 항목.

가소성(물리학)

[lub-1] Lubliner, Jacob (2008), Plasticity Theory, Courier Dover Publications.

[2] 아난다라자(2010년).

[3] Bilby, B. A.; Bullough, R.; Smith, E. (1955), "Continuous distributions of dislocations: a new application of the methods of non-Riemannian geometry", Proceedings of the Royal Society A, 231 (1185): 263–273, Bibcode:1955RSPSA.231..263B, doi:10.1098/rspa.1955.0171

[4] Kröner, E. (1958), "Kontinuumstheorie der Versetzungen und Eigenspannungen", Erg. Angew. Math., 5: 1–179

[5] Lee, E. H. (1969), "Elastic-Plastic Deformation at Finite Strains" (PDF), Journal of Applied Mechanics, 36 (1): 1–6, Bibcode:1969JAM....36....1L, doi:10.1115/1.3564580^{[영구적 데드링크]}

[6] Anand, L. (1979), "On H. Hencky's approximate strain-energy function for moderate deformations", Journal of Applied Mechanics, 46 (1): 78–82, Bibcode:1979JAM....46...78A, doi:10.1115/1.3424532

[1]

[2]

[3]

[4]

[5]

Search

유동소성 이론

네임스페이스

더

목차

소변형 이론

흐름 규칙

일관성 조건

대변형 이론

승소성소성 운동학

탄성계통

흐름 규칙

로드 언로드 조건

일관성 조건

참조

참고 항목.