모어 서클

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "Mohr's circle" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2014년 12월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

Mohr의 원은 Cauchy 스트레스 테스터에 대한 변환 법칙을 2차원 그래픽으로 표현한 것이다.

Mohr의 원은 재료의 강도에 대한 기계공학, 토양의 강도에 대한 지질공학, 건축구조물의 강도에 대한 구조공학 등과 관련된 계산에 종종 사용된다. 또한 수직 및 수평 구성 요소로 감소시켜 많은 평면에서 응력을 계산하는 데도 사용된다. 이것들은 주응력이 계산되는 주응력이라고 불린다. 모어의 원은 또한 그래픽 표현에서 주응력과 주응력을 찾는 데 사용될 수 있으며, 그렇게 하는 가장 쉬운 방법 중 하나이다.^[1]

연속체로 가정된 물질 본체에 대한 응력 분석을 수행한 후, 특정 물질 지점에서 Cauchy 응력 텐서의 구성 요소는 좌표계와 관련하여 알려져 있다. 그런 다음 Mohr 원을 사용하여 회전 좌표계에 작용하는 응력 성분, 즉 그 지점을 통과하는 다른 방향의 평면에 작용하는 응력 성분을 그래픽으로 결정한다.

원 위의 각 점의 압시사와 세로좌표(${\displaystyle {\sigma n\mathrm{}}_{}}$ ${\$${\displaystyle {\tau n\mathrm{}}_{}}$ ${\$는 회전 좌표계에 작용하는 정상 응력 및 전단 응력 성분의 크기이다. 즉, 원은 모든 방향에서 개별 평면의 스트레스 상태를 나타내는 점의 중심점이며, 여기서 축은 스트레스 요소의 주요 축을 나타낸다.

19세기 독일의 엔지니어 칼 컬만은 벤딩 중 수평 빔의 종방향 및 수직적 스트레스를 고려하면서 스트레스에 대한 그래픽 표현을 최초로 구상했다. 그의 작품은 동료 독일인 엔지니어인 크리스티안 오토 모어(서클의 이름)에게 영감을 주었는데, 이들은 이를 2차원적, 3차원적 스트레스로 확장해 스트레스 서클에 기초한 실패 기준을 개발했다.^[2]

한 지점에서 스트레스 상태를 표현하기 위한 대안적인 그래픽 방법으로는 라메의 스트레스 타원체 및 카우치 스트레스 사분면이 있다.

Mohr 원은 관성 텐서의 변형률과 모멘트를 포함하여 모든 대칭 2x2 텐서 행렬에 적용할 수 있다.

동기

내부 힘은 변형 가능한 물체의 입자 사이에서 생성되며, 연속체로 가정되며, 외부 힘, 즉 표면 힘 또는 신체 힘 중 하나에 대한 반응이다. 이 반응은 입자에 대한 뉴턴의 운동 법칙과 동등한 연속체에 대한 오일러의 운동 법칙에서 따온 것이다. 이러한 내부 힘의 강도를 측정하는 것을 스트레스라고 한다. 물체는 연속체로 가정되기 때문에 이러한 내부 힘은 물체의 체적 내에 연속적으로 분포한다.

예를 들어 구조, 기계 또는 지질공학과 같은 공학에서, 물체 내의 응력 분포, 예를 들어 터널 주위의 암석 질량, 비행기 날개 또는 건물 기둥의 응력 분포를 스트레스 분석을 통해 결정한다. 응력 분포를 계산하는 것은 물체의 모든 점(물질 입자)에서 응력을 결정하는 것을 의미한다. Cauchy에 따르면, 연속체로 가정된 물체의 어느 지점에서의 응력은 Cauchy 스트레스 텐서라고 알려진 타입(2$,$0)의 2차 텐서$\sigma {\displaystyle \mathit{}}$ i ${\displaystyle j_{}}$ ${\$$displaystyle$ $\$$sigma$ $_{ij}$의 9가지 스트레스 성분으로 완전히 정의된다$.$

${\displaystyle{\boldsymbol{\sigma}}=\left[{\begin{매트릭스}\sigma_{11}&\sigma_{12}&\sigma_{13}\\\sigma_{21}&\sigma_{22}&\sigma_{23}\\\sigma_{31}&\sigma_{32}&\sigma_{33}\\\end{매트릭스}}\right]\equiv\left-LSB-{\begin{행렬}\sigma _{xx}&, \sigma _{xy}&, \sigma _{xz}\\\sigma _{yx}&, \sigma _{yy}&, \sigma _{yz}\\\s.igma _{zx}&, \sigma _{zy}&, \sigma _{zz}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{x}&\tau _{xy}&\tau _{xz}\\\tau _{yx}&\sigma _{y}&\tau _{yz}\\\tau _{zx}&\tau _{zy}&\sigma _{z}\\\end{matrix}}\right]}$

좌표계$({\displaystyle x}$, ${\displaystyle y}$) ${\displaystyle(x,y)}$에 대해 객체 내의 응력 분포를 결정한 후 회전 좌표계$({\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$, y ${\displaystyle {\prime }^{}}$) ${\displaystyle$ $P}$의 특정 재료점에서 응력 텐서 $성분$을 계산해야 할 수 있다$.$$스타일(x',y')},$즉, 관심 지점을 통과하는 방향이 다른 평면에 작용하는 응력 - 좌표계$({\displaystyle x}$, y${\displaystyle }$) ${\displaystyle(x,y$)}(그림 3)와 각도를 형성한다.$$ 예를 들어, 최대 정상 응력과 최대 전단 응력뿐만 아니라 작용하는 평면의 방향을 찾는 것이 중요하다. 이를 달성하기 위해서는 좌표계의 회전하에서의 텐서 변환이 필요하다. 텐서(tensor)의 정의로부터, 카우치 스트레스 텐서(cauchy stress tensor)는 텐서(tensor) 변환 법칙을 준수한다. Cauchy 스트레스 테스터에 대한 이 변환 법칙의 그래픽 표현은 스트레스에 대한 Mohr circle이다.

2차원 응력 상태에 대한 모어의 원

2차원에서는 어떤 두 개의 수직 방향과 관련하여$$ 주어진 재료 $지점{\displaystyle }$ P ${\displaystyle P}$의 응력 텐서는 오직 세 가지 응력 구성요소로 완전히 정의된다. 특정 좌표계$({\displaystyle x}$, ${\displaystyle y}$) ${\displaystyle (x,y$$$$)}$의 경우, 이러한$$ 스트레스 성분은 정상 응력 $\sigma {\displaystyle {}_{}}$ ${\displaystyle x_{}}$ ${\$ 및 ${\displaystyle {\sigma }_{}}$ y ${\$ $\$$sigma$ $_{y$$}$이며$,$ 각운동량의 균형으로부터 $τ$ x ${\$이다.y 스트레스 텐서(stress tensor)를 입증할 수 있다. 이 대칭은 $\tau {\displaystyle {}_{}}$ ${\displaystyle x_{}}$ ${\displaystyle y_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle y_{}}$ ${\displaystyle x_{}}$ ${\$을(를) 암시한다$.$ 따라서 Cauchy 스트레스 텐서는 다음과 같이 쓸 수 있다.

${\displaystyle {\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{x}&\tau _{xy}&0\\\tau _{xy}&\sigma _{y}&0\\0&0&0\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{x}&\tau _{xy}\\\tau _{xy}&\sigma _{y}\\\end{matrix}}\right]}$

The objective is to use the Mohr circle to find the stress components ${\displaystyle \sigma _{\mathrm {n} }}$ and ${\displaystyle \tau _{\mathrm {n} }}$ on a rotated coordinate system ${\displaystyle (x',y')}$, i.e., on a differently oriented plane passing through ${\displaystyle P}$ $x{\displaystyle }$ ${\displaystyle x}$- ${\displaystyle }$ ${\displaystyle y}$ 평면과$$ 수직이다(그림 4). 회전 좌표계$({\displaystyle {}^{}}$ ${\displaystyle \prime ,}$ y ${\displaystyle {\prime }^{}}$) ${\displaystyle (x',y')}$은(는) 원래 좌표계$($${\displaystyle x}$, ${\displaystyle y}$) ${\displaystyle$ $\theta }$을(를$)$ 사용하여$$ 각도를 $\theta {\displaystyle }$ ${\$displaystyle $\x$,y}로$$ 만든다.

모어 원의 방정식

평면 응력과 평면 변형률의 2차원 사례에 대한 Mohr 원의 방정식을 도출하려면 먼저 $재료{\displaystyle }$ 점 $P{\displaystyle }$ ${\displaystyle P}($그림 4) 주위에 y ${\displaystyle y}$- z ${\displaysty z}$ 면에$$ 평행한 방향의 단위 면적을 갖는 2차원 극소수 재료 요소를 고려하십시오..,, 페이지 또는 화면에 수직이다.

최소소자에 대한 힘의 평형으로부터 정상응력 ${\displaystyle {\sigma n\mathrm{}}_{}}$ ${\$ 및$$ 전단응력 ${\displaystyle {\tau n\mathrm{}}_{}}$ ${\$은(는) 다음을 통해 주어진다$$.

${\displaystyle \mathrma _{\mathrm {n}={\frac {1}{1}2}}(\fracma _{x}+\fracma _{y})+{1}{1}{1}{1}:{x}-\ma _\cos 2\ta +\tau_{xy}sin 2}ta }ta }ta }ta.$

${\displaystyle \tau_{\mathrm{n}}=-{\frac {1}{1}:{2}}(\ma _{x}-\ma _{y})\sin 2\teta +\cos 2\xy}$

모어의 원 파라메트릭 방정식 도출 - 힘의 평형

${\displaystyle {\sigma n\mathrm{}}_{}}$ ${\displaystyle$ $\sigma _{\mathrm{n}}}($${\displaystyle {}^{}}$′ ${\$ -축$$)(그림 4) 방향의 힘의 평형으로부터 ${\displaystyle {\sigma n\mathrm{}}_{}}$ ${\$ 작용하는$$ 평면의 면적이 $DA}$인 것을 알 수 있다$.$ ${\displaystyle \\begin{aigned}\sum F_{x'}&=\sigma _{\mathrm {n}{dA-\sigma _{x}d.A\cos ^{2}\theta -\sigma _{y}dA\sin ^{2}\theta -\tau _{xy}d.A\cos \theta \sin \theta -\tau _{xy}dA\sin \theta \cos \theta =0\\\sigma _{\mathrm {n} }&=\sigma _{x}\cos ^{2}\theta +\sigma _{y}\sin ^{2}\theta +2\tau _{xy}\sin \theta \cos \theta \\\end{aligned}}}$ 그러나, 그것을 아는 것은 ${\displaystyle \cos ^{2}\theta ={\frac {1+\cos 2}{2}},\qquad \cos 2}{1-\cos 2\cos 2}{2}}\cos \text}\csin 2\cos \cosa \ta \ta}$ 우리는 얻는다. ${\displaystyle \mathrma _{\mathrm {n}={\frac {1}{1}2}}(\fracma _{x}+\fracma _{y})+{1}{1}{1}{1}:{x}-\ma _\cos 2\ta +\tau_{xy}sin 2}ta }ta }ta }ta.$ 이제 ${\displaystyle {\tau n\mathrm{}}_{}}$ ${\$$displaystyle$ $\tau _{\mathrm{n}}}}}($${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\$ y$'}$ -축$$)(그림 4) 방향의 힘의 평형으로부터 ${\displaystyle {\tau n\mathrm{}}_{}}$ ${\$${\$$mathrmatrm}}}}}}}}}}}}}$이 작용하는 평면의 면적이 $DA}$인 것을 알 수 있다$.$ ${\displaystyle \\begin{aigned}\sum F_{y'}&=\tau _{\mathrm {n}}}dA+\sigma _{x}d.A\cos \theta \sin \theta -\sigma _{y}dA\sin \theta \tau_{xy}d.A\cos ^{2}\theta +\tau _{xy}dA\sin ^{2}\theta =0\\\tau _{\mathrm {n} }&=-(\sigma _{x}-\sigma _{y})\sin \theta \cos \theta +\tau _{xy}\left(\cos ^{2}\theta -\sin ^{2}\theta \right)\\\end{aligned}}}$ 그러나, 그것을 아는 것은 $\displaystyle \coses ^{2}\theta -\sin ^{2}\theta =\cos 2\text{and}\qquad \sin 2\theta = 2\sin \theta \cos }$ 우리는 얻는다. ${\displaystyle \tau_{\mathrm{n}}=-{\frac {1}{1}:{2}}(\ma _{x}-\ma _{y})\sin 2\teta +\cos 2\xy}$

두 방정식 모두 알려진 카우치 스트레스 텐서(Cauchy stress tensor)에 텐서 변환 법칙을 적용하여 얻을 수 있는데, 이는 ${\displaystyle {nn\mathrm{}}_{}}$ ${\$와 ${\displaystyle {and\mathrm{}}_{}}$ ${\$의 방향으로 힘의 정적 평형을 수행하는 것과 같다.

모어의 원 파라메트릭 방정식 도출 - 텐서 변환

스트레스 텐서 변환 법칙은 다음과 같이 말할 수 있다. ${\displaystyle{\begin{정렬}{\boldsymbol{\sigma}}'&, =\mathbf{A}{\boldsymbol{\sigma}}{A}^ᆯ\\\left[{\begin{매트릭스}\sigma_{x'}&\tau_{x'y의}\\\tau_{y'x의}&\sigma_{y'}\\\end{매트릭스}}\right]& \mathbf, =\left[{\begin{매트릭스}a_{x}&a_{xy}\\a_{yx}&a_{y}\\\end{매트릭스}}\right]\left는 경우에는{\begin{행렬}\sigma _{)}&,\tau _{xy}\\\.타우 _{yx}&, \sigma _{y}\\\end{매트릭스}\오른쪽]\왼쪽[{\put}a_{x}&a_{yx}\\a_{xy}\a_{xy}&a_{y}\end{fined}}\right]\\\\&=\left[{\begin{matrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \\\end{matrix}}\right]\left[{\begin{matrix}\sigma _{x}&\tau _{xy}\\\tau _{yx}&\sigma _{y}\\\end{matrix}}\right]\left[{\begin{matrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{matrix}}\right]\end{aligned}}}$ 오른쪽을 확장하고, $\sigma {\displaystyle {}_{}}$ ${\displaystyle {x{}^{}}_{}}$ ${\displaystyle {{\prime }^{}}_{}}$ =${\displaystyle {}_{}{}_{}}$ ${\displaystyle {n\mathrm{}}_{}}$ ${\$$mathrm$${n}}}}}$ 및$$ ${\displaystyle {x{}^{}}_{}}$ x${\displaystyle {{}^{}}_{}}$′ x${\displaystyle {{}^{}}_{}}$\${\displaystyle {}_{}}$= ${\displaystyle {nn\mathrm{}}_{}}${\$displaystyle \tau_{x'$y'=\$tau$ $\displaystyle \cos \cos _{\mathrm {n}=\cosma ^{2}\theta +\cosma ^{2}\theta +2\tau _{xy}\sin \to_{xy}\ta \cos \ta }$ 그러나, 그것을 아는 것은 ${\displaystyle \cos ^{2}\theta ={\frac {1+\cos 2}{2}},\qquad \cos 2}{1-\cos 2\cos 2}{2}}\cos \text}\csin 2\cos \cosa \ta \ta}$ 우리는 얻는다. ${\displaystyle \mathrma _{\mathrm {n}={\frac {1}{1}2}}(\fracma _{x}+\fracma _{y})+{1}{1}{1}{1}:{x}-\ma _\cos 2\ta +\tau_{xy}sin 2}ta }ta }ta }ta.$ $\displaystyle \tau_{\mathrm {n}-(\mathma _{x}-\ma _{y})\sin \cos \cos \cos \cos \cos \theta +\ta \{2}\sin \data \right}$ 그러나, 그것을 아는 것은 $\displaystyle \coses ^{2}\theta -\sin ^{2}\theta =\cos 2\text{and}\qquad \sin 2\theta = 2\sin \theta \cos }$ 우리는 얻는다. ${\displaystyle \tau_{\mathrm{n}}=-{\frac {1}{1}:{2}}(\ma _{x}-\ma _{y})\sin 2\teta +\cos 2\xy}$ $\sigma {\displaystyle {}_{}}$ $′{\$$displaystyle \sigma _{y}}$ action x perpendicular{\$displaystyle \sigma _{x}}}$의 작용 면에 수직으로$$ 작용하는 응력 성분 $\sigma {\displaystyle {}_{}}$ y${\displaystyle {{}^{}}_{}}$σ${$}을 계산할 필요는 없다$$.

이 두 방정식은 모어 원의 파라메트릭 방정식이다. 이 방정식에서는 ${\displaystyle \mathrm{2\theta }}$ ${\displaystyle 2\theta}$이(가) 매개변수이고$$, ${\displaystyle {\sigma n\mathrm{}}_{}}$ ${\$과(와) ${\displaystyle {\tau n\mathrm{}}_{}}$ ${\$이 좌표가 된다. 즉, abscissa ${\displaystyle {\sigma n\mathrm{}}_{}}$ ${\$${\mathrm{n}}}}$이(가) 있는 좌표계를 선택하고$$$\tau {\displaystyle }$ ${\displaystyle \ta}$ 매개 변수에 값을 지정하면 획득한 포인트가 원 위에 놓이게 된다$$.

이러한 파라메트릭 방정식에서 파라미터$$ $2{\displaystyle \mathrm{}}$ ${\displaystyle \theta }$ ${\displaystyle 2\theta }$을(를) 제거하면 Mohr 원의 비모수 방정식이 산출된다. 이는 ${\displaystyle {\sigma n\mathrm{}}_{}}$ ${\$ 및$$ ${\displaystyle {nn\mathrm{}}_{}}${\$displaystyle \tau_{\mathrm{n$에 대한 방정식을 재정렬하고 먼저 첫 번째 방정식의 양쪽을 제곱한 후 추가함으로써 달성할 수 있다. 그러므로, 우리는

${\displaystyle {\begin{aligned}\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})\right]^{2}+\tau _{\mathrm {n} }^{2}&=\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}\\(\sigma _{\mathrm {n} }-\sigma _{\mathrm {avg} })^{2}+\tau _{\mathrm {n} }^{2}&=R^{2}\end{aligned}}}$

어디에

${\displaystyle R={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}\quad {\text{and}}\quad \sigma _{\mathrm {avg} }={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})}$

이것은 형태의 원(모어 원)의 방정식이다.

${\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}}$

with radius ${\displaystyle r=R}$ centered at a point with coordinates ${\displaystyle (a,b)=(\sigma _{\mathrm {avg} },0)}$ in the ${\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}$ coordinate system.

서명 규칙

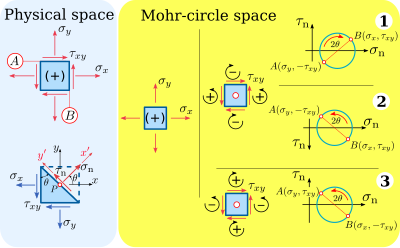
Mohr Circle을 사용할 때 고려해야 하는 두 가지 별도의 기호 규약이 있다. "물리적 공간"의 응력 구성요소에 대한 기호 규칙과 "모어-순환 공간"에 있는 스트레스 구성요소에 대한 기호 규칙. 또한, 두 가지 수화 규약 안에서 각각 공학적 역학(구조공학 및 기계공학) 문헌은 지질역학 문헌과는 다른 수화 규약을 따른다. 표준 사인 규약이 없고, 특정 사인 규약의 선택은 당면한 특정 문제에 대한 계산과 해석의 편의에 의해 영향을 받는다. 이러한 사인 규약에 대한 보다 자세한 설명은 아래에 제시되어 있다.

그림 4를 사용한 Mohr Circle 방정식의 이전 도출은 공학 역학 기호 규약을 따른다. 이 기사에 공학적 역학 표지 규약이 사용될 것이다.

물리적 공간 부호 규칙

Cauchy 스트레스 텐서(그림 3과 그림 4)의 규약에서 스트레스 성분의 첫 번째 첨자는 스트레스 성분의 작용하는 면을 나타내며, 두 번째 첨자는 스트레스 성분의 방향을 나타낸다. $따라서{\displaystyle }$ $\tau {\displaystyle {}_{}}$ ${\displaystyle x_{}}$ y ${\$는 $x{\displaystyle }$ ${\displaystyle x}$ -축의$$ 양방향과 y ${\displaysty y}$ -축의$$ 양방향에서 정상 벡터로 얼굴에 작용하는 전단응력이다$$.

물리적 공간 부호 규약에서 양의 정상 응력은 작용 평면(긴장)에 바깥으로, 음의 정상 응력은 작용 평면(압축)에 안쪽에 있다(그림 5).

물리적 공간 부호 규약에서 양의 전단 응력은 축의 양의 방향에서 재료 요소의 양의 면에 작용한다. 또한 양전단 응력은 축의 음방향에서 재료 요소의 음면에 작용한다. 양면에는 축의 양의 방향에서 정상 벡터가 있고, 음면에는 축의 음의 방향에서 정상 벡터가 있다. 예를 들어 전단 응력 $stresses{\displaystyle {}_{}}$ ${\displaystyle x_{}}$ y ${\$ 및$$ ${\displaystyle y_{}}$ y ${\displaystyle x_{}}${\$displaystyle \tau_{yx}}$는 양면에 작용하기 때문에 양성이며$$, $각각{\displaystyle }$ $y{\displaystyle }$ ${\displaysty$ $y$$}$ -축과$$ x ${\displaysty$ x$}$ -축의$$ 양방향에서도 작용한다(그림 3). 마찬가지로 각각의 반대편 전단 응력 ${\displaystyle {stresses}_{}}$ x ${\displaystyle y_{}}$ ${\$ 및 $negative$ ${\displaystyle y_{}}$ x ${\displaystyle x_{}}$ ${\$는 각각 $x{\displaystyle }$ ${\displaystyle x}$ -축과$$ $y{\displaystyle }$ ${\displaysty y}$ -축의$$ 부정적인 방향으로 작용하기 때문에 부호가 있다.

모어-순환-공간 표지 규약

Mohr-circle-space 부호 규약에서 정상 스트레스는 물리적 공간 부호 규약에서 정상 스트레스와 동일한 부호를 가진다: 양의 정상 스트레스는 작용 면에 바깥으로 작용하며, 음의 정상 스트레스는 작용 면에 안쪽으로 작용한다.

그러나 전단 스트레스는 물리적 공간의 컨벤션에 비해 모어 순환 공간에서는 다른 컨벤션 효과를 가진다. Mohr-circle-space 부호 협약에서 양의 전단 응력은 재료 요소를 시계 반대 방향으로 회전시키고, 음의 전단 응력은 재료를 시계 방향으로 회전시킨다. 이렇게 하면 전단 응력 성분 ${\displaystyle {\tau }_{}}$ x y ${\$는 Mohr-circle 공간에서 양성이며$$, 전단 응력 성분 ${\displaystyle y_{}}$ ${\displaystyle y_{}}$ x$${\$displaystyle \tau_{yx}$는 Mohr-circle 공간에서 음성이 된다$$.

Mohr-circle 공간을 그리기 위해 두 가지 옵션이 존재하며, 수학적으로 올바른 Mohr circle을 생성한다.

1. 양의 전단 응력이 위쪽으로 표시됨(그림 5, 기호 컨벤션 #1)
2. 양의 전단 응력은 아래쪽으로 표시된다. 즉, ${\displaystyle {\tau \mathrm{}}_{}}$ n ${\$축이$$ 반전된다(그림 5, 기호 규칙 #2).

위쪽으로 양의 전단 응력을 $플로팅하면$ 모어 원 위의$$ ${\displaystyle \mathrm{각도}}$가 시계 방향으로 $양$의 회전을 하게 되는데$,$ 이는 $물리적$ 공간 규약과 반대되는 것이다$.$ $그렇기$ 때문에 일부 저자들은^[3] 긍정적인 전단 응력을 아래로 플롯하는 것을 선호하는데, 이것은 모어 $원$의 $각도$가 시계 반대 방향으로 $양$의 회전을 하게 하며, 이는 전단 응력에 대한 물리적 공간 관례와 유사하다$.$

모어 원 공간에서 전단 응력 축을 아래로 향하게 하는 "문제"를 극복하기 위해, 양의 전단 응력이 재료 요소를 시계 방향으로 회전시키고 음의 전단 응력이 재료 요소를 시계 반대 방향으로 회전시키는 것으로 가정하는 대체 기호 규약이 있다(그림 5, opt).이온 3) 이 방법으로 양의 전단 응력은 모어 원 공간에서 위쪽으로 표시되며 각도 2 $[\디스플레이$ 스타일 $2\theta }$은 모어 원 공간에서 시계 반대 방향으로 양의 회전을 가진다$$. 이 대체 기호 규약은 양의 전단 응력 ${\displaystyle {\tau n\mathrm{}}_{}}$ ${\$도 시계 반대방향 전단 응력이고 둘$$ 다 아래쪽으로 표시되기 때문에 그림 5의 기호 규약 #2와 동일한 원을 생성한다. 또한 음의 전단 응력 ${\displaystyle {\tau n\mathrm{}}_{}}$ ${\$은 시계방향 전단 응력이며$$, 둘 다 위쪽으로 표시된다.

이 기사는 물리적 공간에 대한 엔지니어링 역학 부호 협약과 Mohr-circle 공간에 대한 대체 부호 협약(그림 5의 기호 협약 #3)을 따른다.

드로잉 모어의 원

그림 4와 같이 연구 대상 물체의$$ $P{\displaystyle }$ ${\displaystyle P}$ 지점에서 스트레스$$ 성분 ${x},$${\displaystyle {\sigma xy}_{}}$ y ${\$$},$$}$을 알고 있다고 가정하면, 다음은 스트레스 상태에 대한 Mohr 원을 구성하는 단계들이다.$T{\displaystyle }$ P ${\displaystyle$ P$\}:$

1. Draw the Cartesian coordinate system ${\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}$ with a horizontal ${\displaystyle \sigma _{\mathrm {n} }}$-axis and a vertical ${\displaystyle \tau _{\mathrm {n} }}$-axis.
2. Plot two points ${\displaystyle A(\sigma _{y},\tau _{xy})}$ and ${\displaystyle B(\sigma _{x},-\tau _{xy})}$ in the ${\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}$ space corresponding to the known stress components on both perpendicular 선택한 기호 규약을 따르는 평면 $A{\displaystyle }$ ${\displaystyle A}$ 및$$ $B{\displaystyle }$ ${\displaystyle$ B$\}($그림 4 및 6)
3. $직선{\displaystyle }$ $B {\$ A$}$ 및 B ${\$$displaystyle$ $B}$을(를$)$ 직선으로 연결하여 원의 직경을 그린다$.$
4. 모어 원을 그리십시오. 원의 중심$$ $O{\displaystyle }$ ${\displaystyle O}$은 지름 $A{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{B}}$ $`{\$의 중간점으로$,$ 이 선의 교차점과 ${\displaystyle {withn\mathrm{}}_{}}$ ${\$축에$$ 해당한다.

주 정규 응력 찾기

주응력의 크기는 원과 ${\displaystyle {\sigma n\mathrm{}}_{}}$ ${\$$displaystyle$ $C$$}$ 및$$ E ${\displaystyle$ E$}($그림 6)의 축으로 원과 교차하는 지점 $C{\displaystyle }$ ${\$$displaystyle \sigma _{\mathrm{n}}}}-$축의$$ 축이다. 주요 주성 응력의 크기 ${\displaystyle {1\mathrm{}}_{}}$ 1${\$}는 항상 이 두 점 중 임의의 임의의 가장 큰 절대값이다$$. 마찬가지로 소주응력 $stress{\displaystyle {}_{}}$ ${\$의 크기는 항상 이 두 점 중 압시사의 절대값이 가장$$ 낮다. 예상대로 이 두 지점의 좌표는 0이며, 이는 주 평면의 전단 응력 성분의 크기에 해당한다. 또는 다음과 같은 방법으로 주응력 값을 찾을 수 있다.

${\displaystyle \sigma _{1}=\sigma _{\max }=\sigma _{\text{avg}}+R}$

${\displaystyle \sigma _{2}=\sigma _{\min }=\sigma _{\text{avg}-R}$

여기서 평균 정규 응력의 크기 $\sigma {\displaystyle {}_{}}$ ${\displaystyle {\text{avg}}_{}}$ ${\$는 다음과$$ 같이 주어지는 $중앙{\displaystyle }$O {\$displaysty$O}의 중심축이다$.$

${\displaystyle \comparma _{\text{avg}}={\tfrac {1}{1}2}}(\probma _{x}+\probma _{y}}}}}})$

그리고 원의 반지름$$ $R{\displaystyle }$ ${\displaystyle R}$의 길이(두 점을 통과하는 원의 방정식에 기초함)는 다음과 같다.

${\displaystyle R={\sqrt}{\\\tfrac {1}{1}:{2}}(\sigma _{x}-\sigma _{y}\오른쪽)^{2}+\tau _{xy}^{xy}2}}:$

최대 및 최소 전단 응력 찾기

최대 및 최소 전단 응력은 각각 원의 가장 높은 지점과 가장 낮은 지점의 좌표에 해당한다. 이 점들은 원의 중심을 통과하는 수직선과 $원$의 교차점에 위치한다$.$ 따라서 최대 및 최소 전단 응력의 크기는 원의 반지름 $R{\displaystyle }$ ${\displaystyle R}$ 값과 같다.

${\displaystyle \tau _{\max,\min }=\pm R}$

임의 평면에서 스트레스 구성 요소 찾기

앞에서 언급한 바와 같이, 2차원 응력 분석이 수행된 후 재료 지점 $P{\displaystyle }$ ${\displaystyle$ P$}$에서 스트레스$$ 성분 ${\displaystyle {\sigma }_{}}$ x ${\$$displaystyle$ $\$$sigma _{x$$\},$$$${\displaystyle {\sigma }_{}}$ $y{\displaystyle {}_{}}$$$${\$을(를) 알 수 있다$.$ 이러한 응력 구성요소는 그림 5와 6에서와 $같이$ P ${\displaystyle P}$을 통과하는$$ 두 개의 $수직면{\displaystyle }$ A ${\displaystyle A}$ 및$$ $B{\displaystyle }$ ${\displaystyle B}$에서 작용한다. The Mohr circle is used to find the stress components ${\displaystyle \sigma _{\mathrm {n} }}$ and ${\displaystyle \tau _{\mathrm {n} }}$, i.e., coordinates of any point ${\displaystyle D}$ on the circle, acting on any other plane ${\displaystyle D}$ passing through ${\displaystyle P}$ making $평면{\displaystyle }$ $B{\displaystyle }$ ${\displaystyle B}$과(와) 각도 { ${\displaystyle \theta$$\}.$ 이를 위해 두 가지 접근법을 사용할 수 있다. 즉, 평면 B와 극 또는 원점이다.

더블 앵글

As shown in Figure 6, to determine the stress components ${\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}$ acting on a plane ${\displaystyle D}$ at an angle ${\displaystyle \theta }$ counterclockwise to the plane ${\displaystyle B}$ on which ${\displaystyle \sigma _{$$x}}$ acts, we travel an angle ${\displaystyle 2\theta }$ in the same counterclockwise direction around the circle from the known stress point ${\displaystyle B(\sigma _{x},-\tau _{xy})}$ to point ${\displaystyle D(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}$, i.e., an 각도 ${\displaystyle 2}$ circle$$${\displaystyle 2\theta},$ Mohr circle에 $있는{\displaystyle \stackrel{}{}}$ O ${\$${\displaystyle \stackrel{}{}}$$OB}}$ $및{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{\mathrm{O<img\; alt="\backslash overline\; \{OB\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/c47439b833ad02d4373aace062393346f44ecca3"\; style="vertical-align:\; -0.338ex;\; width:3.652ex;\; height:3.009ex;">}}}$D {\$displaystyle {\displaystyle {OD}$ 사이의 각도$$.

이중 각도 접근방식은 $P{\displaystyle }$ ${\displaystyle$ P$}($그림 4)을 통과하는 두 물리적 평면에 대한 정상 벡터 사이의$$ 각도 $\theta {\displaystyle }$ ${\displaystyle \theta$}이(가) 해당 응력 지점$({\displaystyle {\sigma n\mathrm{}}_{}}$ ,$$))에 ${\displaystyle {}_{}}$된 두 선 ${\displaystyle {}_{}}$의 $sigma _{n}).$모어 원과 원의 중심에 있는$$ $},\tau _{\mathrm {n}}.$

이러한 이중 각도 관계는 Mohr 원의 파라메트릭 방정식이 2 $[\displaystyle 2\theta }$의 함수라는 사실에서 비롯된다$.$ 또한 그림 5의$$ $P{\displaystyle }$ ${\displaystyle P}$ 주위에 있는$$ 재료 요소의 $평면{\displaystyle }$ A ${\\\\displaystyle A}$과 $B{\displaystyle }${\$displaystyty B}$이 각도로 분리되어 있음을 알 수 있다.${\displaystyle \theta }$= $∘{\$ $\}\}\}\}\}$ 모어 원에서는 $∘{\$각$$(각 2배)으로 표현된다.

평면의 기둥 또는 원점

두 번째 접근방식은 극 또는 평면의 원점이라고 불리는 모어 원의 점을 결정하는 것을 포함한다. 극에서 그려진 모든 직선은 해당 선과 동일한 방향(병렬)으로 기울어진 평면의 스트레스 상태를 나타내는 지점에서 모어 원을 교차한다. 따라서 특정 평면의 스트레스$$ 성분 ${\displaystyle \sigma }$과($) display${\$displaystyle$$$\$sigma _{\mathrm${$n$$}}$을$($를) 알고, 모어 원에 특정$$ 좌표 ${\displaystyle {\sigma n\mathrm{}}_{}}$ ${\$을 통해 해당 평면에 평행하게 선을 그릴 수 있다. 그리고 모어 원과 같은 선의 교차점으로서 극을 찾는다. 예를 들어, 그림 7과 같이 스트레스 구성 요소인 $\sigma {\displaystyle {}_{}}$ ${\displaystyle x_{}}$, ${\$ $,$ $y{\displaystyle {}_{}}$,${\$ $,$ ${\displaystyle x_{}}$ ,${\$ 등이 스트레스 상태에 있다고 가정해 보자. 먼저 $\sigma {\displaystyle {}_{}}$ ${\displaystyle x_{}}$ ${\$의 작용 평면에 평행한$$ $B{\displaystyle }$ 지점 ${\displaystyle B}$에서 선을 그릴 수 있고$,$ 그렇지 않은 경우 ${\displaystyle {\sigma }_{}}$ y ${\$$\$$sigma _{y}}$의 작용 평면에 평행인$$ A $지점$에서 선을 그릴 수 있다$.$ 이 두 선 중 어느 선이든 모어 원과 교차하는 것은 극이다. 극이 결정되면 수직으로 $angle$$[\displaystyle \theta }$ 각도를 만드는 평면에서 스트레스 상태를 찾거나, 다시 말하면 수평면과$$ $[\displaystyle \theta }$을 형성하는 정상적인 벡터가 있는 평면에서 그 평면에 평행인 극으로부터 선을 그릴 수 있다(그림 7 참조). 그 평면의 정규 및 전단 응력은 선과 모어 원 사이의 교차점의 좌표가 된다.

주 평면의 방향 찾기

주 평면이라고도 하는 최대 및 최소 주 응력이 작용하는 평면의 방향은 각 circleBOC와 ∠BOE를 각각 원형으로 측정하고 각 각도의 절반을 취함으로써 결정할 수 있다. 따라서 $O{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{B}}$의${\${OB$}}$과(와$)$ ${\displaystyle \stackrel{}{\mathrm{OC}}}$의 각도 ∠BOC는 주요 주 $평면$이 B$$면 ${\displaystyle$ $\theta_{p}$을(를) 사용하여 만드는$$ 각도 $\theta {\displaystyle {}_{}}$ ${\$ \{p}의 두 배가 된다$$$.$

각도$$ $\theta {\displaystyle {}_{}}$ ${\displaystyle p_{}}$ ${\displaystyle 1_{}}$ ${\$및 $\theta {\displaystyle {}_{}}$ ${\displaystyle p_{}}$ ${\displaystyle 2_{}}$ ${\$도 다음 방정식에서 찾을 수 있다$$.

${\displaystyle \tan 2\tan _{\mathrm {p}}={\frac {2\tau _{xy}}{\fracma _{y}-\ma _{x}}}}}}}}$

이 방정식은 $\theta {\displaystyle {}_{}}$ ${\displaystyle {p\mathrm{}}_{}}$ ${\$에 대한 두 값을 정의하며, 이$$ 값은 ${\displaystyle {90}^{˚}}$ ${\$이다(그림). 이 방정식은 원의 기하학에서 직접 도출하거나, ${\displaystyle {orn\mathrm{}}_{}}$ ${\$에 대한 원의 파라메트릭 방정식을 0(주요 평면의 전단 응력은 항상 0)과$$ 같게 하여 도출할 수 있다.

예

수평면에 대하여 옆면 중 하나의 평면이 10° 방향을 향하도록 하여 그림 8과 그림 9에 나타낸 것과 같은 응력 상태에서 재료 요소를 가정한다. Mohr 원을 사용하여 다음 항목을 찾으십시오.

• 그들의 행동 평면의 방향.
• 동작 평면의 최대 전단 응력 및 방향.
• 수평면의 응력 구성 요소.

스트레스 변환 공식 또는 스트레스 변환 법칙을 사용하여 답을 확인하십시오.

해결책: 물리적 공간에 대한 엔지니어링 역학 부호 규약(그림 5)에 따라 이 예에서 재료 요소에 대한 응력 요소는 다음과 같다.

${\displaystyle \sigma _{x'}=-10{\textrm {MPa}}$

${\displaystyle \sigma _{y'}=50{\textrm {MPa}}$

${\displaystyle {\tau }_{}}$ ${\displaystyle {x{}^{}}_{}}$ ${\displaystyle {{\prime }^{}}_{}}$ ${\displaystyle {y{}^{}}_{}}$ ${\displaystyle {{\prime }^{}}_{}}$= ${\displaystyle 40}$ ${\displaystyle \text{MPa}}$ ${\$

이 특정 스트레스 상태에 대한 ${\displaystyle {}_{}}$ 원을 그리는 단계에 따라 먼저 $\tau {\displaystyle {}_{}}$ ${\displaystyle {n\mathrm{}}_{}}$ ${\$$(\sigma _{\mathrm {n}}},\tau$$_{\mathrm {n}})$을(를) 위쪽 방향으로 그려본다.

그런 다음 그림 8과 그림 9에서와 같이 평면 A와 B의 스트레스 상태를 나타내는 두 점 A(50,40)와 B(10,-40)를 표시한다. 이러한 지점은 재료 요소에서 바깥쪽으로의 양의 정규 응력과 시계방향으로 회전하는 각 평면의 양의 전단 응력을 가정하는 Mohr-circle 공간에 대한 엔지니어링 역학 부호 규약을 따른다. 이렇게 하면 B면에 작용하는 전단 응력은 음이고 A면에 작용하는 전단 응력은 양성이 된다. 원의 지름은 선접합점 A와 B이다. 원의 중심은 이 선과 $\$ {\$displaystyle \sigma _${\$mathrm{n}}}-$축의$$ 교차점이다. 지름의 중심과 길이 둘 다 알고 있기 때문에, 우리는 이 특정한 스트레스 상태에 대해 모어 원을 그릴 수 있다.

${\displaystyle {\sigma n\mathrm{}}_{}}$ ${\$축과$$ 교차하는 두 점 E와 C의 아비사(그림 8 및 그림 9)는 각각 최소 및 최대 정상 응력의 크기이며, E와 C 지점의 서열은 단면과 주요 평면 모두에 작용하는 전단 응력의 크기, 다시 표시한다.시각적으로, 주 비행기의 경우 0이다.

Mohr circle을 사용하는 아이디어는 원의 서로 다른 점에 대한 좌표를 실제로 측정하여 다른 응력 구성요소를 그래픽으로 찾는 것이지만, 그 결과를 분석적으로 확인하는 것이 더 편리하다. 따라서 원 중심부의 반지름과 압시사는 다음과 같다.

${\displaystyle {\reasoned}R&={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}\\&={\sqrt {\left[{\tfrac {1}{2}}(-10-50)\right]^{2}+40^{2}}}\\&=50{\textrm {MPa}\\\end{arged}}}$

${\displaystyle {\reged}\mathrm {avg} }&={\tfrac {1}{1}{1}{1}:{x}+\frama _{y}\&={\tfrac {1}2}}(-10+50)\\\\&=20{\textrm {MPa}\\\end{aigned}}}$

그리고 주된 스트레스는

${\displaystyle {\begin}\sigma _{1}&=\sigma _{{1}&={\mathrm {avg}}+R\\&=70{\textrm {MPa}\\ended}}}}}}$

${\displaystyle {\begin}\sigma _{2}&=\sigma _{\mathrm {avg} }-R\&=-30{\textrm {MPa}\\\ended}}}}}}$

H 지점과 G 지점의 좌표(그림 8과 그림 9)는 각각 최소 및 최대 전단 응력의 크기이며, H 지점과 G 지점의 아비사(abscissas)는 각각 최소 및 최대 전단 응력이 작용하는 동일한 평면에 작용하는 정상 응력의 크기이다. 최소 및 최대 전단 응력의 크기는 다음과 같이 분석적으로 확인할 수 있다.

${\displaystyle \tau _{\max ,\min }=\pm R=\pm 50{\textrm {MPa}}}$

최소 및 최대 전단 응력 작용이 ${\displaystyle {\mathrm{act}}_{}}$ ${\displaystyle {v\mathrm{}}_{}}$ ${\displaystyle {\mathrm{g}}_{}}$ ${\$\ \$ma _{\mathrm {avg}}}$인 동일한 평면에 작용하는 정상 응력

주 일반 응력과 주 전단 응력의 방향을 찾기 위해 이중 각도 접근법(그림 8) 또는 극 접근법(그림 9)을 사용할 수 있다.

이중 각도 접근법을 사용하여 Mohr Circle(그림 8)에서 ∠BOC 및 ∠BOE 각도를 측정하여 물리적 공간에서 평면 B로 주요 주응력과 사소한 주응력이 이루는 각도의 두 배를 찾는다. 이러한 각도에 대해 보다 정확한 값을 얻기 위해 각도를 수동으로 측정하는 대신 분석 식을 사용할 수 있다.

${\displaystyle {\begin{aligned}2\theta _{\mathrm {p} }=\arctan {\frac {2\tau _{xy}}{\sigma _{x}-\sigma _{y}}}=\arctan {\frac {2*40}{(-10-50)}}=-\arctan {\frac {4}{3}}\end{aligned}}}$

한 가지 해결책은: $2{\displaystyle \mathrm{}}$ ${\displaystyle {\theta }_{}}$ p${\displaystyle {}_{}}$=${\displaystyle }$-${\displaystyle {53.13}^{}}$ ${\displaystyle {\circ }^{}}$ ${\$ 그림 8의 검사에서 이 값은 ∠BOE 각도에 해당한다. 따라서 소주각은 다음과 같다.

${\displaystyle \theta _{p2}=-26.565^{\cHB }}}$

그렇다면 주요 원각은 다음과 같다.

$_{p1}&=180-53.13^{\properties }}=1998.87^{\pa }\\\theta _{p1}&=63.435^{pair }\\ended}}}}}}$

이 특정 예제에서 $\theta {\displaystyle {}_{}}$ ${\displaystyle {\mathrm{p}}_{}}$ 1 ${\$ 및$$ $\theta {\displaystyle {}_{}}$ ${\displaystyle {\mathrm{p}}_{}}$ ${\displaystyle 2_{}}$ ${\$ $\sigma {\displaystyle {}^{}}$ ${\displaystyle {x{}^{}}_{}}$$\{\$$sigma_{x$$$$'}}}}}}}$의 작용 평면에 대한 각도가 아니라는$$ 점을 기억하십시오.${\displaystyle {\sigma }_{}}$ ${\displaystyle x_{}}$ ${\$$xis{\displaystyle }$ 방향: ${\displaystyle x}$ -축$$).

폴 접근법을 이용하여 먼저 폴 또는 평면의 원점을 국부화한다. 이를 위해 우리는 모어 원에 A 지점을 통과하여 가로와 10° 기울어진 선을 그리거나, 다시 말해서 $\sigma {\displaystyle {}_{}}$ $′{\$가 작용하는$$ 평면 A에 평행한 선을 그린다. 폴은 이 선이 모어 원과 교차하는 곳이다(그림 9). 극의 위치를 확인하기 위해 ${\displaystyle {\sigma {}^{}}_{}}$ x ${\displaystyle {{\prime }^{}}_{}}$ ${\$가 작용하는$$ 평면 B에 평행한 모어 원 위에 B 지점을 통과하는 선을 그릴 수 있었다. 이 선은 또한 극에서 모어 원을 교차시킬 것이다(그림 9).

극에서, 우리는 모어 서클에 다른 점들에 선을 그린다. 이러한 선들이 Mohr 원을 교차하는 점의 좌표는 선과 동일한 기울기를 갖는 물리적 공간에서 평면에 작용하는 응력 구성요소를 나타낸다. 예를 들어 극에서 원 안의 C 지점까지의 선은 $\sigma {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$1}가 작용하는$$ 물리적 공간의 평면과 동일한 기울기를 가진다. 이 평면은 Mohr-circle 공간과 물리적 공간에서 모두 평면 B와 63.435°의 각도를 만든다. 같은 방법으로, 선은 같은 방향의 평면에서 스트레스 성분을 찾기 위해 극에서 E, D, F, G, H 지점까지 추적된다.

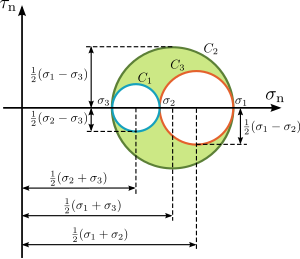
일반적인 3차원 스트레스 상태에 대한 모어의 원

To construct the Mohr circle for a general three-dimensional case of stresses at a point, the values of the principal stresses ${\displaystyle \left(\sigma _{1},\sigma _{2},\sigma _{3}\right)}$ and their principal directions ${\displaystyle \left(n_{1},n_{2},n_{3}\ri$$ght)}$을(를) 먼저 평가해야 한다$$.

, 일반 x1{\displaystyle x_{1}대신}좌표 시스템처럼 주축을 고려하면, x2{\displaystyle x_{2}}, x3{\displaystyle x_{3}}좌표계, σ 1을을 가정해;σ 2>σ 3{\displaystyle \sigma_{1}>, \sigma _{2}>, \sigma _{3}}, 그 후 정상이다. 과 전단 co단위 벡터 $n{\displaystyle \mathbf{}}$ ${\$$mathbf {T} ^{{(\$$mathbf {n}$ $)\}\}$의 응력 벡터 $T{\displaystyle {\mathbf{}}^{}}$ ${\displaystyle {n\mathbf{}}^{}}$)의 성분들은 다음 방정식을 만족한다$.$

${\displaystyle {\begin{aligned}\left(T^{(n)}\right)^{2}&=\sigma _{ij}\sigma _{ik}n_{j}n_{k}\\\sigma _{\mathrm {n} }^{2}+\tau _{\mathrm {n} }^{2}&=\sigma _{1}^{2}n_{1}^{2}+\sigma _{2}^{2}n_{2}^{2}+\sigma _{3}^{2}n_{3}^{2}\end{aligned}}}$

${\displaystyle \mathrm {n} }=\mathma _{1}^{1}^{1}{1}^{1}+\n_{2}^{2}^{3}n_{3}^{3}^{3}}}}}}}.}$

${\displaystyle n_{}}$ i${\displaystyle {}_{}}$= n ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$+ ${\displaystyle {n\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$+ ${\displaystyle {}_{}^{}}$ 3 ${\displaystyle {}_{}^{}}$= ${\displaystyle 1}$ ${\displaystyle n_{i}n_{i}=n_{1}^{2}+n_{2$}임을 알고 있음$}^{2}+n_{3$$}^{2}=1$ n ${\displaystyle {1\mathrm{}}_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ ${\$n ${\displaystyle {\mathrm{}}_{}^{}}$ ${\displaystyle {2\mathrm{}}_{}^{}}$ ${\$ n ${\displaystyle {3\mathrm{}}_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ ${\$ 산출되는 가우스 제거법을 사용하여 해결할 수 있다$.$

${\displaystyle{\begin{정렬}n_{1}^{2}&, ={\frac{\tau_{\mathrm{n}}^ᆲ+(\sigma_{\mathrm{n}}-\sigma_{2})(\sigma_{\mathrm{n}}-\sigma_{3})}{(\sigma_{1}-\sigma_{2})(\sigma_{1}-\sigma_{3})}}\geq 0\\n_{2}^{2}&, ={\frac{\tau_{\mathrm{n}}^ᆷ+(\sigma_{\mathrm{n}}-\sigma_{3})(\sigma_{\mathrm{n}}-\sigma_{1})}{(\sigma_{2}-\s.igma_{3})(\sigma _{2}-\sigma _{1})}}\geq 0\\n_{3}^{2}&={\frac {\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{1})(\sigma _{\mathrm {n} }-\sigma _{2})}{(\sigma _{3}-\sigma _{1})(\sigma _{3}-\sigma _{2})}}\geq 0.\end{정렬}}}$

> > ${\$ _${3$${\displaystyle }$(${\displaystyle {}_{}}$ ${\displaystyle i_{}{}^{}}$ ${\displaystyle {2\mathrm{}}^{}}${\$displaystyle (n_{i}^{2}})$는 음수가 아니므로$$ 이들 방정식의 분자는 만족한다.

τ n2+(σ n− σ 2)(σ n− σ 3)≥ 0{\displaystyle \tau_{\mathrm{n}}^ᆭ+(\sigma_{\mathrm{n}}-\sigma_{2})(\sigma_{\mathrm{n}}-\sigma_{3})\geq 0}일 경우는 분모 1− σ 2을 σ;0{\displaystyle \sigma_{1}-\sigma _{2}>0}과σ 1− σ 3>0{\displaystyle \sigma_{1}-.\sig$ma _{3}>0}$

τ n2+(σ n− σ 3)(σ n− σ 1)≤ 0{\displaystyle \tau_{\mathrm{n}}^ᆭ+(\sigma_{\mathrm{n}}-\sigma_{3})(\sigma_{\mathrm{n}}-\sigma_{1})\leq 0}일 경우는 분모 σ 2− σ 3>0{\displaystyle \sigma_{2}-\sigma _{3}>0}과σ 2− σ 1<0{\displaystyle \sigma_{2}-.\sig$ma _{1}<0}$

τ n2+(σ n− σ 1)(σ n− σ 2)≥ 0{\displaystyle \tau_{\mathrm{n}}^ᆭ+(\sigma_{\mathrm{n}}-\sigma_{1})(\sigma_{\mathrm{n}}-\sigma_{2})\geq 0}일 경우는 분모 3− σ 1<>σ;0{\displaystyle \sigma_{3}-\sigma _{1}<0}과σ 3− σ 2<0.{\displaystyle \sigma_{3}.-\si$gma _{2}<0.$$}$

이 표현들은 다음과 같이 다시 쓸 수 있다.

${\displaystyle {\begin{aligned}\tau _{\mathrm {n} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{2}+\sigma _{3})\right]^{2}\geq \left({\tfrac {1}{2}}(\sigma _{2}-\sigma _{3})\right)^{2}\\\tau _{\mathrm {n} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{1}+\sigma _{3})\right]^{2}\leq \left({\tfrac {1}{2}}(\sigma _{1}-\sigma _{3})\right)^{2}\\\tau _{\mathrm {n} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{1}+\sigma _{2})\right]^{2}\geq \left({\tfrac {1}{2}}(\sigma _{1}-\sigma _{2})\right)^{2}\\\end{aligned}}}$

which are the equations of the three Mohr's circles for stress ${\displaystyle C_{1}}$, ${\displaystyle C_{2}}$, and ${\displaystyle C_{3}}$, with radii ${\displaystyle R_{1}={\tfrac {1}{2}}(\sigma _{2}-\sigma _{3})}$, ${\displaystyle R_2=\frac{1}{2}({\sigma }_1-{\sigma }_3}$${\displaystyle R_{2}={\tfrac {1}{2}}(\sigma _{1}-\sigma _{3})}$, and ${\displaystyle R_{3}={\tfrac {1}{2}}(\sigma _{1}-\sigma _{2})}$, and their centres with coordinates ${\displaystyle \left[{\tfrac {1}{2}}(\sigma _{2}+\sigma _{3}),0\right]}$, ${\displaystyle \left[{\tfrac {1}{2}}(\sigma _{1}+\sigma _{3}),0\right]}$, ${\displaystyle \left[{\tfrac {1}{2}}(\sigma _{1}+\sigma _{2}),0\right]}$, respectively.

Mohr 원에 대한 이러한 방정식은 모든 허용 응력점$({\displaystyle }$ ${\displaystyle {nn}_{}}$, ${\displaystyle {nn}_{}}$)$${\$displaystyle$(\$sigma$ _${\mathrm {n}},\tau$ _${\mathrm {n}}}})$이 이러한 원 또는 원들에 의해 둘러싸인 음영 영역 내에 놓여 있음을 보여준다(그림 10 참조). Stress points ${\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}$ satisfying the equation for circle ${\displaystyle C_{1}}$ lie on, or outside circle ${\displaystyle C_{1}}$. Stress points ${\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {$$n} })}$ satisfying the equation for circle ${\displaystyle C_{2}}$ lie on, or inside circle ${\displaystyle C_{2}}$. And finally, stress points ${\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}$ satisfying the equation for circle ${\displaystyle C_{3}}$ lie on, 또는 외부 원 ${\displaystyle {C\mathrm{}}_{}}$ ${\$

참고 항목

• 임계 평면 분석

참조

참고 문헌 목록

• Beer, Ferdinand Pierre; Elwood Russell Johnston; John T. DeWolf (1992). Mechanics of Materials. McGraw-Hill Professional. ISBN 0-07-112939-1.
• Brady, B.H.G.; E.T. Brown (1993). Rock Mechanics For Underground Mining (Third ed.). Kluwer Academic Publisher. pp. 17–29. ISBN 0-412-47550-2.
• Davis, R. O.; Selvadurai. A. P. S. (1996). Elasticity and geomechanics. Cambridge University Press. pp. 16–26. ISBN 0-521-49827-9.
• Holtz, Robert D.; Kovacs, William D. (1981). An introduction to geotechnical engineering. Prentice-Hall civil engineering and engineering mechanics series. Prentice-Hall. ISBN 0-13-484394-0.
• Jaeger, John Conrad; Cook, N.G.W.; Zimmerman, R.W. (2007). Fundamentals of rock mechanics (Fourth ed.). Wiley-Blackwell. pp. 9–41. ISBN 978-0-632-05759-7.
• Jumikis, Alfreds R. (1969). Theoretical soil mechanics: with practical applications to soil mechanics and foundation engineering. Van Nostrand Reinhold Co. ISBN 0-442-04199-3.
• Parry, Richard Hawley Grey (2004). Mohr circles, stress paths and geotechnics (2 ed.). Taylor & Francis. pp. 1–30. ISBN 0-415-27297-1.
• Timoshenko, Stephen P.; James Norman Goodier (1970). Theory of Elasticity (Third ed.). McGraw-Hill International Editions. ISBN 0-07-085805-5.
• Timoshenko, Stephen P. (1983). History of strength of materials: with a brief account of the history of theory of elasticity and theory of structures. Dover Books on Physics. Dover Publications. ISBN 0-486-61187-6.

외부 링크

위키다양성은 모어의 서클에 대한 학습 자원을 가지고 있다.

위키미디어 커먼즈에는 모어의 서클과 관련된 미디어가 있다.

• 레베카 브레넌의 모어 서클과 더 많은 서클
• DoITPoMS 교육 및 학습 패키지 - "스트레스 분석 및 모어의 서클"