올로그

정보 매핑
토픽과 필드
비즈니스 의사결정 맵핑 데이터 시각화 그래픽 커뮤니케이션 인포그래픽스 정보 설계 지식 시각화 멘탈 모델 형태학적 분석 스키마(심리학) 시각 분석 시각 언어
노드 링크 어프로치
인수 맵 클래디스트리스 인지 지도 개념 격자 개념도 개념 그래프 Decision Tree(결정 트리) 덴드로그램 그래프 그리기 쌍곡선 트리 하이퍼텍스트 이슈맵 이슈 트리 레이어드 그래프 그리기 마인드 맵 객체 역할 모델링 온톨로지(정보과학) 조직도 방사형 트리 시멘틱 네트워크 소시오그램 타임라인 토픽 맵 트리 구조
「 」를 참조해 주세요.
설계 근거 도식적 추론 엔티티-관계 모델 지구 가시화 개념 및 마인드 맵핑 소프트웨어 목록 올로그 온톨로지 문제 구조화 방법 시멘틱 웹 트리밍 못된 문제
v t

ologs 이론은 범주 이론, 언어 및 그래픽 도구를 사용하여 지식 표현, 과학 모델의 구성 및 데이터 저장을 위한 엄격한 수학적 프레임워크를 제공하려는 시도입니다.올로그는 MIT 수학과의 연구 과학자 데이비드 스피박에 ^[1]의해 2010년에 도입되었다.

어원학

"olog"라는 용어는 "ontology log"의 줄임말입니다.'온톨로지'는 그리스어 '존재', 즉 '존재', 동사 '베'의 현재 분사, '-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'-'에서 유래한다.

수학적 형식주의

특정 도메인에 대한 $olog{\displaystyle \mathcal{}}$ C$(\$는 해당 도메인에 관련된 구(구체적으로는 단일 부정명사구)로 라벨이 지정된 상자이며, 그 상자 사이의 모피션은 영역과 관련된 동사구(동사구)로 라벨이 지정된 상자입니다.이 명사와 동사 구절들은 결합되어 도메인 내의 사물들 사이의 관계를 표현하는 문장을 형성합니다.

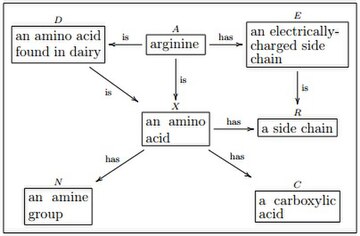
모든 olog에서 개체는 대상 범주 내에 있습니다.특별히 지정하지 않는 한 대상 카테고리는 세트 및 함수 카테고리인 Set$\$로 간주됩니다.위 그림의 상자는 세트$(\$의 객체를 나타냅니다. 예를 들어, "아미노산"이라는 문구가 들어 있는 상자는 모든 아미노산 집합을 나타내며, "사이드 체인"이라는 문구가 들어 있는 상자는 모든 사이드 체인 집합을 나타냅니다."아미노산"에서 "옆사슬"을 가리키는 "has"라는 라벨이 붙은 화살표는 각 아미노산을 고유한 옆사슬에 매핑하는 기능을 나타냅니다.

사용할 수 있는 다른 대상 카테고리는 파워셋 모나드의 Kleisli $카테고리{\displaystyle {\mathcal{}}_{}}$ ${\displaystyle C_{\mathbb{}}}$ P$(\$mathbb {$P}})$입니다.$A{\displaystyle o}$ ${\displaystyle \mathrm{Ob}}$( ${\displaystyle \mathbf{\text{Set}}}$)$${ $displaystyle$A \ $in$ Ob ( { \ $textbf${ $Set$} ) }$$, 、${\displaystyle }$P ( ${\displaystyle A}$)$$（ \ $displaystyle$ \$mathbb${ P$}$ ( A ) $set$ A의 파워셋이 됩니다.$자연변환{\displaystyle }$ $【{$$displaystyle \eta$$}$는 $A】$를 싱글톤${\displaystyle }${$a}({$displaystyle \{$a$에 $매핑$하고, $자연변환{\displaystyle }$μ({$displaystyle \mu})$는 세트를 조합에 매핑합니다.Kleisli $카테고리{\displaystyle {\mathcal{}}_{}}$ ${\displaystyle C_{\mathbb{}}}$ P$(\$는 P$(\$와 일치하는 오브젝트 및 바이너리 관계를 확립하는 모르피즘을 가진 카테고리입니다.${\displaystyle \mathrm{형태론}}$f : A ${\displaystyle \to }$ {\$displaystyle$f:$A$${\displaystyle \backslash }$$toB$및 $A{\displaystyle \backslash }$$displaystyle$ A$\in$ B$\backslash$$displaystyle$ B$\in$ B\$displaystyle$ R$\displaystyle$ R$\$displaystyle $R\$in$R$\$displaystyle$ R$\$$displaystyle$ F($a$를 ${\displaystyle \mathrm{정의}}$합니다.이 대상 범주와 함께 사용되는 동사 문구는 하위 집합인 개체(예: " is related to" 또는 " is greater than")에 대해 의미가 있어야 합니다.

다른 가능한 목표 범주는 Giry 모나드라고 ^[2]불리는 확률 분포의 클라이슬리 범주입니다.이것은 마르코프 결정 과정의 일반화를 제공한다.

Olog 및 데이터베이스

$olog{\displaystyle \mathcal{}}$ C$(\$는 데이터베이스 스키마로도 볼 수 있습니다.olog 내의 모든 상자(C$\style$ {$C$의 객체)는 $테이블{\displaystyle }$T(\$display style$ T$$$)$이며, 상자에서 나오는 화살표(모형)는 C$(\$의 열입니다. C$(\displaystyle$ {$C})$의 객체에 대한 특정 인스턴스 할당은 f를 통해 수행됩니다.$unctor{\displaystyle }$I : ${\displaystyle \mathbf{\text{C}}}$ ${\displaystyle \to }$\ $displaystyle$ I : { \ $mathcal${$$C$$} \ $to$ \ $textbf${ $Set$}$$$。$위의 예에서 "아미노산" 상자는 아미노산 종류와 같은 행의 수이고, 그 상자에서 나오는 화살표에 대해 열 수가 각각 1열씩인 표로 나타납니다.

olog 간의 관계

실제로 다른 모델이나 세계관 간의 커뮤니케이션이 될 수 있는 다른 올로그 간의 "커뮤니케이션"은 펑터를 사용하여 이루어집니다.스피박은 '의미있는' 함수와 '강력하게 의미있는' ^[1]함수의 개념을 결합한다.C$(\displaystyle$ {$C})$와 D$(\$를 2개의 olog로 $하고{\displaystyle \mathcal{}}$, $I{\displaystyle :C\mathcal{}}$ ${\displaystyle \to }$ $Set$ {\$mathcal {C}을($를) \$displaystyle$ I$:{\mathbf {Set$로 설정}, $J{\displaystyle :D\mathcal{}}$ ${\displaystyle \to }$ {\$style$ J$:{\mathcal$ {D}을$($를) {textcal {D$}$로 설정합니다$.$$$펑터$(functor)$에게 보내는 $것입니다.$${\displaystyle F}$ ${\displaystyle$ F$}$는 스키마 맵핑이라고 불립니다.우리는 자연 $변환{\displaystyle }$ m${\displaystyle :}$ ${\displaystyle I}$ ${\displaystyle \to }$ ${\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$J { display style m: I → F ${\displaystyle {}^{}}$ J { $display$ m$}$가 존재한다면$$F { $display$ $style$ F$}$는 의미가 있다고 말합니다.$I\to$ F$^{*}J($J x F의 풀백).

예를 $들어{\displaystyle \mathcal{}}$ C$(\displaystyle${$C$})와 D$(\displaystyle {D})$를 두 가지 다른 과학 모델로 하여 $펑터{\displaystyle }$F(\$displaystyle$ F$)$는 첫 번째 $모델$C(\displaystyle {Set$})$에 의해 만들어진 세트$(\$의 객체인 "예측"에 의미가 있다.cal ${C}}$은(는) 두 번째 $모델{\displaystyle \mathcal{}}$ D$(\$로 변환할 수 있습니다.

$F{\displaystyle }$(${\displaystyle displaystyle\mathcal{}}$ F${\displaystyle )}$는${\displaystyle }$$객체{\displaystyle }$ X$(\$ X$\in\mathcal {C})$가 ${\displaystyle \mathrm{주어지면}}$I(${\displaystyle X}$)$=$)=$J(X)$가 $있다고{\displaystyle }$ 합니다$.$이는$$m\$display$ m이$$ $자연$동형이어야 하는 것과 $같습니다{\displaystyle }$.

C$($ 스타일$)$에서 $D{\displaystyle \mathcal{}}$$($$디스플레이$스타일$)$로 $이어지는{\displaystyle \mathcal{}}$ 의미 있는 $펑터{\displaystyle }$ F$(디스플레이 스타일$ F$)$를 찾기 어려울 수 있습니다. 이 경우 C$($ 스타일$)$의 공통 $기반$을 나타내는 새로운 $olog{\displaystyle \mathcal{}}$ B$($를 정의하려고 할 수 있습니다.$C}}$ 및$$ $({$ 및$$ D({$displaystyle$ {D}) 및 ${\displaystyle {D(\{}_{}}$displaystyle $F_{\$mathcal {$C}}):$ ${\displaystyle B\mathcal{}}$${\displaystyle \to }$ $(\style F_${\$mathcal${C$}):$${C})$의 ${\displaystyle 의미\mathcal{}}$ 있는 $함수$를 ${\displaystyle {찾습니다.}_{}}$

olog 간의 통신이 위에서 설명한 바와 같이 양방향 통신으로 제한되는 경우 ologs 컬렉션은 그래프의 노드로, 엣지는 ologs를 연결하는 함수로 생각할 수 있습니다.두 개 이상의 olog 간에 동시 통신이 허용되면 그래프는 대칭 단순 복합체가 됩니다.

모범 사례의 규칙

스피박은 형태론이 기능적인 성질을 가진 올로그를 쓰기 위한 몇 가지 모범적 실무 규칙을 제공한다(수학적 형식주의 ^[1]섹션의 첫 번째 예 참조).상자의 텍스트는 다음 규칙을 준수해야 합니다.

1. 단어 "a" 또는 "an"으로 시작합니다. (예: "아미노산")
2. olog의 저자에 의해 만들어지고 인식되는 구별을 말한다.
3. 범위가$\displaystyle{textbf$ {Set$\}\}$인 펑터가 잘 정의된 구별을 말한다. 즉, 예를 들어, 모든 아미노산 집합이 존재한다.
4. 복합 구조에서 모든 변수를 선언합니다.(예: 상자에 "남자와 여자"라고 쓰는 대신 "$남자$ m$\displaystyle$ m$"$ 및$$ "$여자{\displaystyle }$ ${\displaystyle w}$$\displaystyle$ w$"$라고 적습니다. $여기$서${\displaystyle }$m$\displaystyle$m은$$ $남자{\displaystyle }$, ${\displaystyle w}$$\displaystyle$$w$는 여자입니다.)

처음 세 가지 규칙은 olog 작성자가 정의한 개체(상자)가 제대로 정의된 집합임을 확인합니다.네 번째 규칙은 olog의 화살표에 대한 레이블을 개선합니다.

적용들

이 개념은 데이비드 스피박 등이 바이오나노사이언스 2011년 12월호에 발표한 논문에서 거미줄과 음악 구성의 과학적 ^[3]유추를 규명하기 위해 사용됐다.

「 」를 참조해 주세요.

• 하이퍼그래프
• 모델링 언어
• 온톨로지 언어
• 오퍼라드 이론
• 조직학
• 유니버설 대수
• 보편 논리

레퍼런스

외부 링크

• Spivak, David I. "Categorical informatics". math.mit.edu. Retrieved 2 May 2017.
• Spivak, David I. (2014). Category theory for the sciences. Cambridge, MA: MIT Press. ISBN 9780262028134. OCLC 876833252.