하이퍼그래프
Hypergraph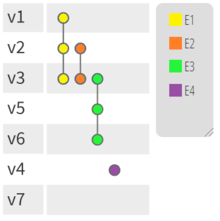
수학에서 하이퍼그래프는 모서리가 임의의 수의 꼭지점을 결합할 수 있는 그래프의 일반화입니다.반면 일반 그래프에서는 모서리가 정확히 두 개의 정점을 연결합니다.
형식적으로 무방향 H({H})는 쌍 ( H=(입니다. 여기서 X({ X는 노드 또는 정점이라고 하는 요소의 이고 E({E}는 (무방향 하이퍼그래프에서)는 비어 있지 않은displaystyle H)의 집합입니다. E E는 P {display{ { } ( X ) \ \{ \ \ \ style { }。P는 X의 멱집합입니다.정점 집합의 크기를 하이퍼 그래프의 순서라고 하며, 가장자리 집합의 크기는 하이퍼 그래프의 크기입니다.
다이렉트 하이퍼그래프는 하이퍼지 세트가 아니라 하이퍼지 테일 및 헤드를 구성하는 X X 순서쌍이라는 점에서 다릅니다.
그래프 가장자리는 2개의 노드만 연결하는 반면 하이퍼지(hyperedge)는 임의의 수의 노드를 연결합니다.단, 하이퍼그래프는 모든 하이퍼그래프가 동일한 카디널리티를 갖는 하이퍼그래프를 연구하는 것이 바람직하다.k-균일 하이퍼그래프는 모든 하이퍼그래프가 크기 k를 갖는 하이퍼그래프이다(즉, 하이퍼그래프 중 하나는 세트의 집합이며, 각 하이퍼그래프는 k 노드를 연결하는 하이퍼그래프이다).2개의 균일한 하이퍼그래프는 그래프이고 3개의 균일한 하이퍼그래프는 순서가 없는 3개의 집합입니다.무방향 하이퍼그래프는 집합 시스템 또는 유니버설 집합에서 추출된 집합의 집합 패밀리라고도 합니다.
하이퍼그래프는 발생 구조로 볼 수 있다.특히, 모든 하이퍼그래프에 대응하는 초당 "인시던스 그래프" 또는 "레비 그래프"가 있으며, 반대로, 전부는 아니지만 대부분의 초당 그래프는 하이퍼그래프의 발생 그래프로 간주할 수 있다.
하이퍼그래프는 다른 많은 이름을 가지고 있다.계산기하학에서, 무방향 하이퍼그래프는 때때로 범위 공간이라고 불리고, 하이퍼지들은 [2]범위라고 불릴 수 있습니다.협동 게임 이론에서 하이퍼그래프는 단순한 게임(투표 게임)이라고 불리며, 이 개념은 사회적 선택 이론의 문제를 해결하기 위해 적용됩니다.일부 문헌에서는 에지를 하이퍼링크 또는 [3]커넥터라고 부릅니다.
하이퍼그래프 컬렉션은 하이퍼그래프 동형사상이 형태인 범주이다.
적용들
무방향 하이퍼그래프는 만족도 문제,[4] 데이터베이스,[5] 기계 [6]학습 및 Steiner 트리 [7]문제와 같은 모델링에 유용합니다.이들은 데이터 모델과 분류기 정규화(수학)[8]로 기계 학습 작업에서 광범위하게 사용되어 왔다.애플리케이션에는 추천 시스템([9]하이퍼지로서의 커뮤니티), 이미지 검색(하이퍼지로서의 상관 관계) 및 바이오 인포매틱스([10][11]하이퍼지로서의 생물 화학적 상호작용)가 포함됩니다.대표적인 하이퍼그래프 학습 기술에는 하이퍼그래프 라플라시안([12]Hypergraph Laplacian)으로 스펙트럼 그래프 이론을 확장하는 하이퍼그래프 스펙트럼 클러스터링과 학습 [13]결과를 제한하기 위해 추가적인 하이퍼그래프 구조 비용을 도입하는 하이퍼그래프 반감독 학습이 포함된다.대규모 하이퍼그래프의 경우 Apache Spark를 사용하여 구축된 분산[6] 프레임워크도 사용할 수 있습니다.
다이렉트 하이퍼그래프는 텔레포니애플리케이션,[14][15] 자금세탁 검출, 운용조사,[16] 수송계획 등의 모델링에 사용할 수 있습니다.또한 Horn-satifiability를 [17]모델링하는 데도 사용할 수 있습니다.
그래프에서 개념의 일반화
그래프와 관련된 많은 정리 및 개념은 하이퍼그래프, 특히 다음과 같은 개념에도 적용된다.
- 하이퍼그래프에서의 매칭
- 하이퍼그래프의 정점 커버(횡단이라고도 함);
- 하이퍼그래프의 선 그래프
- 하이퍼그래프 문법 - 하이퍼그래프 클래스를 치환 규칙 세트로 보강하여 작성됩니다.
- 램지의 정리
- 에르데스-코-라도 정리
- 균일한 하이퍼그래프에 대한 Kruskal-Katona 정리
- 하이퍼그래프에 대한 홀형 정리.
유도 하이퍼그래프: 과도 폐쇄 및 최단 경로 [16]문제.
하이퍼그래프 도면
비록 하이퍼그래프가 그래프보다 종이에 그리는 것이 더 어렵지만, 몇몇 연구자들은 하이퍼그래프의 시각화를 위한 방법을 연구해왔다.
평면상의 곡선이 그래프 에지를 묘사하기 위해 사용되는 표준 그래프 그리기 스타일과 유사한 하이퍼그래프의 가능한 시각적 표현 중 하나에서 하이퍼그래프의 정점은 점, 디스크 또는 상자로 묘사되며, 하이퍼그래프는 정점을 [18][19]잎으로 하는 나무로 묘사된다.정점이 점으로 표시되는 경우, 하이퍼지는 점 세트를 연결하는 부드러운 원곡선 또는 [20][21][22]점 세트를 둘러싼 단순 닫힌 원곡선으로 표시될 수도 있습니다.
하이퍼그래프 시각화의 또 다른 스타일, 하이퍼그래프 [23]그림의 세분화 모델에서는 평면을 영역으로 세분화하며, 각 영역은 하이퍼그래프의 단일 정점을 나타냅니다.하이퍼그래프의 하이퍼지는 이러한 영역의 연속된 하위 집합으로 나타나며, 색칠, 주변 윤곽선 또는 둘 다로 나타낼 수 있습니다.예를 들어 순서 n Venn 다이어그램은 하이퍼그래프 하위 분할 도면으로서 n개의 하이퍼그래프(그림의 정의 곡선)와n 2-1개의 정점(이러한 곡선이 평면을 세분화하는 영역으로 표현)을 가진 것으로 볼 수 있다.평면 그래프의 다항 시간 인식과는 대조적으로 하이퍼그래프가 평면 분할 [24]도면을 가지고 있는지 여부를 판단하는 것은 NP-완전이지만 영역의 인접 패턴이 경로, 주기 또는 [25]트리로 구속되었을 때 이 유형의 도면의 존재를 효율적으로 테스트할 수 있다.
PAOH라고 하는[1] 하이퍼그래프의 대체 표현은 이 문서의 맨 위에 있는 그림에 나와 있습니다.모서리는 정점을 연결하는 수직선입니다.정점은 왼쪽에 정렬되어 있습니다.오른쪽 범례에는 모서리의 이름이 표시됩니다.동적 하이퍼그래프용으로 설계되었지만 간단한 하이퍼그래프에도 사용할 수 있습니다.
하이퍼그래프 컬러링
고전적인 하이퍼그래프 컬러링이란 의모든 정점에 {2, 3, }({2 3, ...\의 색상 중 하나를 할당하여 각 하이퍼그래프의 각 정점에 각각 다른 색상의 정점이 2개 이상 포함되도록 하는 것입니다.즉, 카디널리티가 2 이상인 단색 하이퍼지(hyperedge)는 없어야 합니다.이런 의미에서 이것은 그래프 색상의 직접적인 일반화이다.모든 색상에 걸쳐 사용되는 구별되는 색상의 최소 수를 하이퍼그래프의 색수라고 합니다.
최대 k개의 색상을 사용하는 하이퍼그래프는 k-colorable이라고 합니다.2색 하이퍼그래프는 정확히 초당파입니다.
고전적인 하이퍼그래프 컬러링에는 많은 일반화가 있습니다.그 중 하나는 단색의 가장자리가 허용될 때 소위 혼합 하이퍼그래프 컬러링입니다.일부 혼합 하이퍼그래프는 색상 수에 관계없이 색칠할 수 없습니다.무색성의 일반적인 기준은 알려져 있지 않습니다.혼합 하이퍼그래프가 색을 칠할 수 있는 경우, 사용된 색상의 최소 수와 최대 수를 [26]각각 하한 및 상한 색수라고 합니다.
하이퍼그래프 속성
하이퍼그래프는 다음과 같은 다양한 속성을 가질 수 있습니다.
- 비어 있음 - 가장자리가 없습니다.
- 단순하지 않음(또는 복수) - 루프(단일 정점으로 하이퍼링됨) 또는 반복된 에지가 있습니다. 즉, 동일한 정점 집합을 포함하는 에지가 둘 이상 있을 수 있습니다.
- 심플 - 루프가 없고 반복되는 에지가 없습니다.
- - d - regular - 모든 정점에는 도d가 있습니다.즉, 하게 d d hyperedge에 포함되어 있습니다.
- 2-colorable - 카디널리티가 최소 2개인 하이퍼지(hyperedge)가 양쪽 클래스의 정점을 적어도 1개 포함하도록 정점을 2개의 클래스 U와 V로 분할할 수 있습니다.또 다른 용어는 속성 B이다.
- 두 가지 더 강한 특성은 초당적이고 균형적이다.
- \ k \ displaystyle k( hyperedge )각 하이퍼지는 정확하게의 합니다.
- \ k} - partite -정점은 k \ k 부분으로 되며 각 하이퍼지는 각 유형의 정점을 정확히 1개 포함합니다.
- 모든 k k 부분 하이퍼그래프(2의 경우)는 k k2의 경우)가 균일하고 2색상은 2색입니다.
- 하향 닫힘 - 방향성이 없는 하이퍼그래프의 모든 가장자리 부분 집합도 하이퍼지입니다.하향 폐쇄형 하이퍼그래프는 보통 추상 단순 복합체라고 불립니다.
- 증가 특성을 가진 추상적인 단순 복합체를 매트로이드라고 한다.
관련 하이퍼그래프
하이퍼그래프 링크는 임의의 카디널리티를 가질 수 있기 때문에 서브하이퍼그래프, 부분하이퍼그래프 및 섹션하이퍼그래프라고 불리는 서브그래프 개념에는 몇 가지 개념이 있습니다.
( ,) { H=(을(를) 정점으로 구성된 하이퍼그래프로 합니다.
엣지 세트를 가지고 있다
서 I v{ _ { } i _ { e 、 respect 、 각각 정점과 모서리의 인덱스 세트입니다.
하위 하이퍼그래프는 일부 정점이 제거된 하이퍼그래프입니다.공식적으로 AX {\ \ X }에 의해 유도되는 는 다음과 같이 정의된다.
대체 용어로 H to [27]: 468 A를 들 수 있습니다.
서브하이퍼그래프의 확장자는 에 부분적으로 포함된 H H의 각 하이퍼게지가 확장 A {\ Ex에 완전히 포함되어 있는 하이퍼그래프입니다. 정식으로.
- x ( A ) ( ){ Ex ( H{ A ) = ( \ A ' , E ' ) \ A ' \ { ' ) 、
부분 하이퍼그래프는 일부 가장자리가 [27]: 468 제거된 하이퍼그래프입니다.엣지 인덱스 세트의 J I{ \ J \ I _ { } a 、J { J}에 의해 되는 부분 하이퍼그래프는 하이퍼그래프입니다.
AX { A \ 를 지정하면 섹션 하이퍼그래프는 부분 하이퍼그래프입니다.
H})의 듀얼 H H는 정점과 가장자리가 서로 교환되는 하이퍼그래프이며, 정점은 {displaystyle \로 지정되며, 가장자리는 m로 지정됩니다
다음과 같이 평등의 개념이 적절히 정의되어 있는 경우, 하이퍼그래프의 이중화를 취하는 연산은 혁신이다.
접속 하이퍼그래프 H와 같은 정점을 가지는 접속 그래프 G는, H의 하이퍼 엣지 마다 G내의 접속 서브 그래프가 유도되면, H의 호스트 그래프가 된다.분리된 하이퍼그래프 H에 대해 G의 연결성분과 H의 연결성분 G'가 대응하는 H'의 호스트인 경우 G는 호스트그래프이다.
하이퍼그래프의 2-섹션(또는 그래프, 원시 그래프, 가이프만 그래프를 나타내는 클리크 그래프)은 하이퍼그래프의 동일한 정점과 동일한 하이퍼그래프에 포함된 모든 정점 쌍 사이의 모서리를 가진 그래프입니다.
발생행렬
{ 1 , , , n { V = \ { v { v _ { { { { _ { { { { v _ { { { { { v _ {1} ,{ n \ } } e e e e e , 、 \ { , , } , { _ { 1 , { 1 } , { 2 } , { } , { } } } ~ { } } }} \ ldots }
무방향 하이퍼그래프의 I ( ) { I = ( _ { } } 。
입사 행렬의 t{\ I는의 쌍대라고 불리는 H ( , )( V , , E ) = ( ) V )、 \ H V ) } { { the the the the the the the the the the the the the the the the the the the the the the the the the the ( ( ( V 、 { \ V { *} ∗ ∗ {\ { \ style { }^{ * }\ V { * } 및 E 、 v j、 e \ style { }^ { * * } } 、 { * 。
다이렉트 하이퍼그래프의 경우 각 displaystyle })의 앞면과 뒷면은 각각 [17]H H및 (ej)\ T(e_로 됩니다. ( j) { I = ( _ { } } 。
발생 그래프
하이퍼그래프 H는 집합 X, E는 BG의 일부이며, (x1, e1)는 H의 엣지1 e에 정점1 x가 포함되는 경우에 한하여 엣지에 접속되어 있는 것으로, 다음과 같이 양분 그래프 BG로 나타낼 수 있다.
반대로, 두 번째 부분에 고정된 부분이 있고 연결되지 않은 노드가 없는 초당 그래프는 위에서 설명한 방식으로 하이퍼그래프를 나타냅니다.이 초당 그래프는 발생 그래프라고도 불립니다.
인접 행렬
하이퍼그래프의 인접행렬을 위한 병렬은 그래프의 인접행렬에서 도출할 수 있다.그래프의 경우 인접행렬은 정점의 쌍이 인접해 있는지 여부를 나타내는 정사각형행렬이다.마찬가지로 하이퍼그래프에 대해 ( j) { A = (_ { } )를 정의할 수 있습니다 하이퍼그래프는 하이퍼그래프의 { e { k \ m의 가중치를
사이클
주기 및 비순환 그래프의 단일 자연 개념이 있는 일반 무방향 그래프와 대조적으로, 일반 그래프의 특수한 경우 일반 그래프 비순환성으로 붕괴되는 하이퍼 그래프에 대한 비동일한 자연 정의가 여러 개 있다.
하이퍼그래프에 대한 비순환성의 첫 번째 정의는 클로드 베르게에 [28]의해 제시되었다. 하이퍼그래프는 발생 그래프(위에서 정의된 초당 그래프)가 비순환인 경우 베르게 비순환이다.이 정의는 매우 제한적입니다.예를 들어 하이퍼그래프에 v v , v, v 등 하이퍼게지의 일부 v v이 v v, v f는 과 입사 그래프를 조사함으로써 분명히 직선 시간 내에 베르주 사이클리티를 테스트할 수 있다.
우리는 나중에 α-비순환성이라고 불리는 하이퍼그래프 비순환성의 [5]더 약한 개념을 정의할 수 있다.acyclicity의 생각은 하이퍼 그래프는 것 등각(최초의 그래프의 모든 패거리 몇몇 hyperedge으로 덮여 있다)과 그 원시적인 그래프고 화음의;그것은 또한 GYO algorithm[29][30](또한 그레이엄의 알고리즘으로 알려져), 엄청난 속도로 제거하는 합류하는 반복 과정을 통해 빈 그래프에 변경 가능성에 해당합니다.가장자리 u귀의 일반적 정의를 노래하다데이터베이스 이론의 영역에서 데이터베이스 스키마는 그 기초가 되는 하이퍼그래프가 [31]α-비순환적인 경우 특정한 바람직한 특성을 갖는 것으로 알려져 있다.또, α-비순환성은, 1차 논리의 가드 프래그먼트(guarded fragment)의 발현성과도 관련된다.
하이퍼그래프가 [32]α-비순환인지 선형 시간 내에 테스트할 수 있습니다.
α-비순환성은 α-순환 하이퍼그래프에 하이퍼지(hyperedge)를 추가하면 α-비순환이 될 수 있다는 반직관적인 특성을 갖는다(예를 들어 하이퍼그래프의 모든 정점을 포함하는 하이퍼지(hyperedge)를 추가하면 항상 α-비순환이 된다).부분적으로[33] 이러한 인식된 단점에 의해 동기 부여되어, 로널드 페이긴은 β-비순환성과 β-비순환성의 더 강한 개념을 정의했다.우리는 하이퍼그래프의 모든 하위 하이퍼그래프가 α-비순환이라는 요구사항으로 β-비순환성을 언급할 수 있으며,[30] 이는 Graham의 초기 정의와 동일하다[33].γ-비순환성의 개념은 데이터베이스 스키마의 몇 가지 바람직한 속성과 동등하며 바흐만 다이어그램과 관련이 있는 보다 제한적인 조건이다.β-비순환성과 β-비순환성은 모두 다항식 시간에 시험할 수 있다.
이 네 가지 비순환성 개념은 유사하다.베르제 비순환성은 α 비순환성을 내포하는 β 비순환성을 내포하는 β-비순환성은 β-비순환성을 내포한다.그러나 그 반대의 의미는 존재하지 않기 때문에 이들 4가지 개념은 다르다.[33]
동형, 대칭, 등식
하이퍼그래프 동형사상은 각 엣지가 다른 엣지에 매핑되도록 하이퍼그래프의 정점 집합에서 다른 엣지까지의 지도입니다.
H ( ,) { H = ( , ) }는 G ( ,) { ( , )로 표기된 것과 동형입니다(바이오젝션이 있는 경우).
의치환 을 다음과 같이 설정합니다.
그런 다음 이젝션{\(\을 그래프의 동형이라고 합니다.주의:
- ''' '' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' \ G} \ G { } 。
하이퍼그래프의 가장자리에 명시적으로 라벨을 붙이면 강력한 동형이라는 추가적인 개념을 갖게 된다.치열이 동일하다면 H디스플레이 스타일 H)는 G G와 강하게 동형이라고 할 수 .그런 다음 H (\ H G라고 . 모든 강한 동형 그래프는 동형이지만 그 반대는 아닙니다.
하이퍼그래프의 꼭지점에 명시적으로 라벨을 붙이면 동등성과 동등성의 개념을 갖게 됩니다.H H는 G G와 하며, 동형사상이 있으면 H H G로 표기한다.
그리고.
주의:
- G \ H \ Gand 、 H G \ H^ { * } \ G { * } 。
또한 치환 이 아이덴티티인 경우 H H는 G G와 같으며 HG(\G로 표기됩니다.이러한 평등의 정의에서는 그래프는 자기 정의됩니다.
하이퍼그래프 자기동형은 정점 집합에서 정점 자체의 동형사상으로, 정점의 재라벨링입니다.하이퍼그래프 H(= (X, E))의 자기동형성 집합은 하이퍼그래프 및 필기 Aut(H)의 자기동형성 그룹이라고 불리는 구성 대상 그룹입니다.
예
모서리가 있는 H(\ H를 생각해 보십시오.
그리고.
H와 G G는 분명히 동형이지만(( (스타일 \)=\ 등 강한 동형은 아니다.예를 들어 H H에서는 a a가 가장자리 1, 4, 6을 충족하므로 다음과 같이 됩니다.
G(\ G에는 가장자리 1, 4, 6을 충족하는 정점이 없습니다.
이 예에서는 H H와 G G는 하고 H H G는 H H와 동형적입니다.
대칭
H H의 rH))는 하이퍼그래프 내 에지의 최대 카디널리티입니다.모든 가장자리가 동일한 카디널리티 k를 갖는 경우 하이퍼그래프는 균일하거나 k-균일하다고 하거나 k-하이퍼그래프라고 합니다.그래프는 2개의 균일한 하이퍼그래프일 뿐입니다.
정점 v의 도수 d(v)는 이를 포함하는 가장자리 수입니다.모든 정점에 k도가 있으면 H는 k-규칙입니다.
균일한 하이퍼그래프의 듀얼은 규칙적이며 그 반대도 마찬가지입니다.
의 두 꼭지점 와 y는 (\\와 자기동형이 존재하는 이라고 한다
하이퍼그래프는 모든 정점이 대칭이면 정점-추이적(또는 정점-대칭)이라고 합니다.마찬가지로 하이퍼그래프는 모든 가장자리가 대칭인 경우 에지-추이적입니다.하이퍼그래프가 모서리 대칭과 정점 대칭인 경우 하이퍼그래프는 단순히 추이적입니다.
하이퍼그래프 이중성 때문에 에지-전이성 연구는 정점-전이성 연구와 동일합니다.
파티션
E에 의한 파티션 정리.Dauber는[34] 에지 전이 H (, ) { H = ( , 의 경우 파티션이 존재한다고 말합니다.
X 에 생성된 가 K 1 k마다 전이적이 되도록X(\displaystyle 1\ K의 집합 X(\ X를 지정합니다.
서r (H) \ r ( )는 H의 순위입니다.
결과적으로, 정점 추이가 아닌 에지 추이 하이퍼 그래프는 두 가지 색상입니다.
그래프 분할(특히 하이퍼그래프 분할)은 IC[35] 설계와 병렬 [36][37][38]컴퓨팅에 많은 응용 분야를 가지고 있습니다.효율적이고 확장 가능한 하이퍼그래프 분할 알고리즘은 기계 학습 작업에서 [6]대규모 하이퍼그래프를 처리하는 데도 중요합니다.
추가 일반화
이 섹션은 어떠한 출처도 인용하지 않습니다. 2021년 1월 (이를 에 대해 설명합니다) |
하이퍼그래프의 가능한 일반화 중 하나는 가장자리가 다른 가장자리를 가리키도록 하는 것입니다.이 일반화에는 두 가지 변형이 있습니다.하나의 예에서, 가장자리는 정점의 집합으로 구성될 뿐만 아니라 정점의 하위 집합, 정점의 하위 집합 등을 포함할 수 있습니다.기본적으로 모든 가장자리는 트리의 내부 노드 또는 유도 비순환 그래프일 뿐이며, 정점은 리프 노드입니다.하이퍼그래프는 공통의 공유 노드를 가진 트리 집합일 뿐입니다(즉, 특정 내부 노드 또는 리프(leaf)는 여러 다른 트리에서 발생할 수 있습니다).반대로, 모든 나무 집합은 이 일반화된 하이퍼그래프로 이해될 수 있습니다.나무는 컴퓨터 과학과 수학의 많은 다른 분야들에서 널리 사용되고 있기 때문에, 사람들은 하이퍼그래프가 자연스럽게 나타난다고 말할 수 있다.따라서, 예를 들어, 이러한 일반화는 용어 대수의 모형으로 자연스럽게 발생합니다. 모서리는 항에 대응하고 정점은 상수 또는 변수에 대응합니다.
이러한 하이퍼그래프의 경우 set membership은 주문을 제공하지만, 순위는 전이적이지 않기 때문에 부분 주문도 사전 주문도 아닙니다.이 일반화의 Levi 그래프에 대응하는 그래프는 유향 비순환 그래프입니다.예를 들어, 집합이 { a, b } { V \ { , b \} { _ { } = \ {a , b \ } e { , 1 } { e { 2 } \ { } \ { displaystyle e } \ { } \ a , \ { a } } }인 일반화된 하이퍼그래프를 생각해 보겠습니다.그 후 be1 { 1} 및 { e_ , b e2 b 단, 이러한 하이퍼그래프에 대한 세트멤버십의 전이적 폐쇄는 부분순서를 유도하고 부분순서된 하이퍼그래프로 "평탄화"됩니다.et.
또는 가장자리가 지시된 비순환 그래프에 따라 정렬되어야 하는 요건에 관계없이 가장자리가 다른 가장자리를 가리킬 수 있습니다.따라서 꼭지점을 전혀 포함할 필요가 없는 에지 루프가 있는 그래프를 사용할 수 있습니다.예를 들어 { 2} = { = \ {{ e _ { } = \ { e _ { 2} \ { { e _ {} = = { 1 { style _ { } = { display e _ { { 1 } } } \ } }} } ,,,,,,,,,,,,,,,,,,,,,, { { { { { { { sty엣지인 ets는 기초 공리를 위반합니다.특히, 이러한 하이퍼그래프에 대한 집합 멤버십의 과도적 폐쇄는 없습니다.이러한 구조는 처음에는 이상해 보일 수 있지만, Levi 그래프의 동등한 일반화는 더 이상 초당적이지 않고 오히려 일반적인 방향 그래프에 불과하다는 것을 지적함으로써 쉽게 이해할 수 있다.
이러한 하이퍼그래프에 대한 일반화 발생 행렬은 정의상 정점 + 모서리의 총 개수와 같은 순위의 정사각형 행렬이다.따라서, 위의 예에서, 발생 행렬은 단순하게
「 」를 참조해 주세요.
메모들
- ^ a b Valdivia, Paola; Buono, Paolo; Plaisant, Catherine; Dufournaud, Nicole; Fekete, Jean-Daniel (2020). "Analyzing Dynamic Hypergraphs with Parallel Aggregated Ordered Hypergraph Visualization" (PDF). IEEE Transactions on Visualization and Computer Graphics. IEEE. 26 (1): 12. doi:10.1109/TVCG.2019.2933196. eISSN 1941-0506. ISSN 1077-2626. PMID 31398121. S2CID 199518871.
- ^ 를 클릭합니다Haussler, David; Welzl, Emo (1987), "ε-nets and simplex range queries", Discrete and Computational Geometry, 2 (2): 127–151, doi:10.1007/BF02187876, MR 0884223.
- ^ Pearl, Judea (1984). Heuristics: Intelligent Search Strategies for Computer Problem Solving. Addison-Wesley Publishing Company. p. 25. ISBN 978-0-201-05594-8.
- ^ Feige, Uriel; Kim, Jeong Han; Ofek, Eran (2006). Witnesses for non-satisfiability of dense random 3CNF formulas. 47th Annual IEEE Symposium on Foundations of Computer Science (FOCS'06). IEEE. pp. 497–508. doi:10.1109/FOCS.2006.78.
- ^ a b Beeri, C.; Fagin, R.; Maier, D.; Yannakakis, M. (1983). "On the Desirability of Acyclic Database Schemes" (PDF). Journal of the ACM. 30 (3): 479–513. doi:10.1145/2402.322389. S2CID 2418740.
- ^ a b c Huang, Jin; Zhang, Rui; Yu, Jeffrey Xu (2015), "Scalable Hypergraph Learning and Processing" (PDF), Proceedings of the IEEE International Conference on Data Mining: 775–780, doi:10.1109/ICDM.2015.33, ISBN 978-1-4673-9504-5, S2CID 5130573
- ^ Brazil, M; Zachariasen, M (2015). "Steiner Trees in Graphs and Hypergraphs". Algorithms and Combinatorics. Springer. 29: 301–317. doi:10.1007/978-3-319-13915-9_5. ISBN 978-3-319-13915-9.
- ^ Zhou, Dengyong; Huang, Jiayuan; Scholkopf, Bernhard (2006), "Learning with hypergraphs: clustering, classification, and embedding", Advances in Neural Information Processing Systems, MIT Press, pp. 1601–8, ISBN 9780262256919
- ^ Tan, Shulong; Bu, Jiajun; Chen, Chun; Xu, Bin; Wang, Can; He, Xiaofei (October 2011), "Using rich social media information for music recommendation via hypergraph model", ACM Transactions on Multimedia Computing, Communications, and Applications, 7S (1), Article 22, Bibcode:2011smma.book..213T, doi:10.1145/2037676.2037679, S2CID 432036
- ^ Liu, Qingshan; Huang, Yuchi; Metaxas, Dimitris N. (2013), "Hypergraph with sampling for image retrieval", Pattern Recognition, 44 (10–11): 2255–2262, doi:10.1016/j.patcog.2010.07.014
- ^ Patro, Rob; Kingsoford, Carl (2013), "Predicting protein interactions via parsimonious network history inference", Bioinformatics, 29 (10–11): 237–246, doi:10.1093/bioinformatics/btt224, PMC 3694678, PMID 23812989
- ^ Gao, Tue; Wang, Meng; Zha, Zheng-Jun; Shen, Jialie; Li, Xuelong; Wu, Xindong (2013), "Visual-textual joint relevance learning for tag-based social image search", IEEE Transactions on Image Processing, 22 (1): 363–376, Bibcode:2013ITIP...22..363Y, doi:10.1109/tip.2012.2202676, PMID 22692911, S2CID 7432373
- ^ Tian, Ze; Hwang, TaeHyun; Kuang, Rui (2009), "A hypergraph-based learning algorithm for classifying gene expression and arrayCGH data with prior knowledge", Bioinformatics, 25 (21): 2831–2838, doi:10.1093/bioinformatics/btp467, PMID 19648139
- ^ Goldstein, A. (1982). "A Directed Hypergraph Database: A Model for the Local Loop Telephone Plant". Bell System Technical Journal. 61 (9): 2529–54. doi:10.1002/j.1538-7305.1982.tb03439.x. S2CID 11290643.
{{cite journal}}: CS1 유지보수: 날짜 및 연도(링크) - ^ Ranshous, Stephen; Joslyn, Cliff; Kreyling, Sean; Nowak, Kathleen; Samatova, Nagiza; West, Curtis; Winters, Samuel (2017). Exchange Pattern Mining in the Bitcoin Transaction Directed Hypergraph (PDF). Financial Cryptography and Data Security. Springer. doi:10.1007/978-3-319-70278-0_16.
- ^ a b Ausiello, Giorgio; Laura, Luigi (2017). "Directed hypergraphs: Introduction and fundamental algorithms - A survey". Theoretical Computer Science. 658: 293–306. doi:10.1016/j.tcs.2016.03.016.
- ^ a b Gallo, G.; Longo, G.; Pallottino, S.; Nguyen, S. (1993). "Directed hypergraphs and applications". Discrete Applied Mathematics. 42 (2–3): 177–201. doi:10.1016/0166-218X(93)90045-P.
- ^ 를 클릭합니다Sander, G. (2003), "Layout of directed hypergraphs with orthogonal hyperedges", Proc. 11th International Symposium on Graph Drawing (GD 2003), Lecture Notes in Computer Science, vol. 2912, Springer, pp. 381–6, ISBN 978-3-540-24595-7.
- ^ 를 클릭합니다Eschbach, Thomas; Günther, Wolfgang; Becker, Bernd (2006), "Orthogonal hypergraph drawing for improved visibility" (PDF), Journal of Graph Algorithms and Applications, 10 (2): 141–157, doi:10.7155/jgaa.00122.
- ^ 를 클릭합니다Mäkinen, Erkki (1990), "How to draw a hypergraph", International Journal of Computer Mathematics, 34 (3): 177–185, doi:10.1080/00207169008803875.
- ^ 를 클릭합니다Bertault, François; Eades, Peter (2001), "Drawing hypergraphs in the subset standard", Proc. 8th International Symposium on Graph Drawing (GD 2000), Lecture Notes in Computer Science, vol. 1984, Springer-Verlag, pp. 45–76, doi:10.1007/3-540-44541-2_15, ISBN 978-3-540-41554-1.
- ^ 를 클릭합니다Naheed Anjum, Arafat; Bressan, Stéphane (2017), "Hypergraph Drawing by Force-Directed Placement", 28th International Conference on Database and Expert Systems Applications (DEXA 2017), Lecture Notes in Computer Science, vol. 10439, Springer International Publishing, pp. 387–394, doi:10.1007/978-3-319-64471-4_31, ISBN 978-3-319-64470-7.
- ^ 를 클릭합니다Kaufmann, Michael; van Kreveld, Marc; Speckmann, Bettina (2009), "Subdivision drawings of hypergraphs", Proc. 16th International Symposium on Graph Drawing (GD 2008), Lecture Notes in Computer Science, vol. 5417, Springer-Verlag, pp. 396–407, doi:10.1007/978-3-642-00219-9_39, ISBN 978-3-642-00218-2.
- ^ 를 클릭합니다Johnson, David S.; Pollak, H. O. (2006), "Hypergraph planarity and the complexity of drawing Venn diagrams", Journal of Graph Theory, 11 (3): 309–325, doi:10.1002/jgt.3190110306.
- ^ 를 클릭합니다Buchin, Kevin; van Kreveld, Marc; Meijer, Henk; Speckmann, Bettina; Verbeek, Kevin (2010), "On planar supports for hypergraphs", Proc. 17th International Symposium on Graph Drawing (GD 2009), Lecture Notes in Computer Science, vol. 5849, Springer-Verlag, pp. 345–356, doi:10.1007/978-3-642-11805-0_33, ISBN 978-3-642-11804-3.
- ^ "Vitaly Voloshin: Mixed Hypergraph Coloring Website". spectrum.troy.edu. Retrieved 2022-04-27.
- ^ a b Lovász, László; Plummer, M. D. (1986), Matching Theory, Annals of Discrete Mathematics, vol. 29, North-Holland, ISBN 0-444-87916-1, MR 0859549
- ^ Berge, Claude (1973). Graphs and Hypergraphs. Amsterdam: North-Holland. ISBN 0-7204-2450-X.
- ^ Yu, C. T.; Özsoyoğlu, M. Z. (1979). "An algorithm for tree-query membership of a distributed query" (PDF). Proc. IEEE COMPSAC: 306–312. doi:10.1109/CMPSAC.1979.762509.
- ^ a b Graham, M. H. (1979). "On the universal relation". Technical Report. Toronto, Ontario, Canada: University of Toronto.
- ^ Abiteboul, S.; Hull, R. B.; Vianu, V. (1995). Foundations of Databases. Addison-Wesley. ISBN 0-201-53771-0.
- ^ Tarjan, R. E.; Yannakakis, M. (1984). "Simple linear-time algorithms to test chordality of graphs, test acyclicity of hypergraphs, and selectively reduce acyclic hypergraphs". SIAM Journal on Computing. 13 (3): 566–579. doi:10.1137/0213035.
- ^ a b c Fagin, Ronald (1983). "Degrees of Acyclicity for Hypergraphs and Relational Database Schemes". Journal of the ACM. 30 (3): 514–550. doi:10.1145/2402.322390. S2CID 597990.
- ^ Harary, F. (2018) [1969]. Graph Theory. CRC Press. p. 172. ISBN 978-0-429-96231-8.
We next state a theorem due to Elayne Dauber whose corollaries describe properties of line-symmetric graphs. Note the obvious but important observation that every line-symmetric graph is line-regular.
- ^ Karypis, G., Aggarwal, R., Kumar, V., and Shekhar, S. (March 1999), "Multilevel hypergraph partitioning: applications in VLSI domain", IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 7 (1): 69–79, CiteSeerX 10.1.1.553.2367, doi:10.1109/92.748202.
{{citation}}: CS1 maint: 여러 이름: 작성자 목록(링크) - ^ Hendrickson, B., Kolda, T.G. (2000), "Graph partitioning models for parallel computing", Parallel Computing (Submitted manuscript), 26 (12): 1519–1545, doi:10.1016/S0167-8191(00)00048-X.
{{citation}}: CS1 maint: 여러 이름: 작성자 목록(링크) - ^ Catalyurek, U.V.; Aykanat, C. (1995). A Hypergraph Model for Mapping Repeated Sparse Matrix-Vector Product Computations onto Multicomputers. Proc. International Conference on Hi Performance Computing (HiPC'95).
- ^ Catalyurek, U.V.; Aykanat, C. (1999), "Hypergraph-Partitioning Based Decomposition for Parallel Sparse-Matrix Vector Multiplication", IEEE Transactions on Parallel and Distributed Systems, 10 (7): 673–693, CiteSeerX 10.1.1.67.2498, doi:10.1109/71.780863.
레퍼런스
- Berge, Claude (1984). Hypergraphs: Combinatorics of Finite Sets. Elsevier. ISBN 978-0-08-088023-5.
- Berge, C.; Ray-Chaudhuri, D. (2006). Hypergraph Seminar: Ohio State University, 1972. Lecture Notes in Mathematics. Vol. 411. Springer. ISBN 978-3-540-37803-7.
- "Hypergraph", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Bretto, Alain (2013). Hypergraph Theory: An Introduction. Springer. ISBN 978-3-319-00080-0.
- Voloshin, Vitaly I. (2002). Coloring Mixed Hypergraphs: Theory, Algorithms and Applications: Theory, Algorithms, and Applications. Fields Institute Monographs. Vol. 17. American Mathematical Society. ISBN 978-0-8218-2812-0.
- Voloshin, Vitaly I. (2009). Introduction to Graph and Hypergraph Theory. Nova Science. ISBN 978-1-61470-112-5.
- 이 문서에는 Creative Commons Attribution/Share-Alike License에 따라 라이센스가 부여된 PlanetMath의 하이퍼그래프 자료가 포함되어 있습니다.
외부 링크
- PAOHVis: 동적 하이퍼그래프를 시각화하는 오픈 소스 PAOHVis 시스템.









 쌍
쌍  노드 또는 정점이라고 하는 요소의
노드 또는 정점이라고 하는 요소의 

 X
X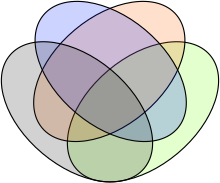
 색상 중 하나를 할당하여 각 하이퍼그래프의 각 정점에 각각 다른 색상의 정점이 2개 이상 포함되도록 하는 것입니다.즉, 카디널리티가 2 이상인 단색 하이퍼지(hyperedge)는 없어야 합니다.이런 의미에서 이것은 그래프 색상의 직접적인 일반화이다.모든 색상에 걸쳐 사용되는 구별되는 색상의 최소 수를 하이퍼그래프의 색수라고 합니다.
색상 중 하나를 할당하여 각 하이퍼그래프의 각 정점에 각각 다른 색상의 정점이 2개 이상 포함되도록 하는 것입니다.즉, 카디널리티가 2 이상인 단색 하이퍼지(hyperedge)는 없어야 합니다.이런 의미에서 이것은 그래프 색상의 직접적인 일반화이다.모든 색상에 걸쳐 사용되는 구별되는 색상의 최소 수를 하이퍼그래프의 색수라고 합니다. 
















 정점과 가장자리가 서로 교환되는 하이퍼그래프이며, 정점은 {
정점과 가장자리가 서로 교환되는 하이퍼그래프이며, 정점은 { 지정되며, 가장자리는
지정되며, 가장자리는  지정됩니다
지정됩니다
























 다음과 같이 설정합니다.
다음과 같이 설정합니다.
 그래프의
그래프의 
 강하게 동형이라고 할 수
강하게 동형이라고 할 수 
 표기한다.
표기한다.





 가장자리 1, 4, 6을 충족하므로 다음과 같이 됩니다.
가장자리 1, 4, 6을 충족하므로 다음과 같이 됩니다.


 하이퍼그래프 내 에지의 최대 카디널리티입니다.모든 가장자리가 동일한 카디널리티 k를 갖는 경우 하이퍼그래프는 균일하거나 k-균일하다고 하거나 k-하이퍼그래프라고 합니다.그래프는 2개의 균일한 하이퍼그래프일 뿐입니다.
하이퍼그래프 내 에지의 최대 카디널리티입니다.모든 가장자리가 동일한 카디널리티 k를 갖는 경우 하이퍼그래프는 균일하거나 k-균일하다고 하거나 k-하이퍼그래프라고 합니다.그래프는 2개의 균일한 하이퍼그래프일 뿐입니다. 




 K
K


 일반화된 하이퍼그래프를 생각해 보겠습니다.그 후 b
일반화된 하이퍼그래프를 생각해 보겠습니다.그 후 b






![\left[ \begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix} \right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/79d672ab411be80685171269d9b0630a4b7dad56)


