렌즈
Lens

렌즈는 굴절에 의해 광선을 집속시키거나 분산시키는 투과형 광학 장치입니다.단순 렌즈는 투명한 물질의 한 조각으로 구성된 반면, 복합 렌즈는 일반적으로 공통 축을 따라 배열된 여러 개의 단순 렌즈(요소)로 구성됩니다.렌즈는 유리나 플라스틱과 같은 재료로 만들어지며, 연마, 또는 필요한 모양으로 성형됩니다.초점을 맞추지 않고 빛을 굴절시키는 프리즘과 달리 렌즈는 빛을 집중시켜 상을 만들 수 있습니다.마이크로파 렌즈, 전자 렌즈, 음향 렌즈 또는 폭발 렌즈와 같이 가시광선 이외의 파동과 방사선을 유사하게 집속시키거나 분산시키는 장치를 "렌즈"라고도 합니다.
렌즈는 망원경, 쌍안경, 카메라와 같은 다양한 영상 기기에 사용됩니다.그것들은 또한 근시나 고메트로피아와 같은 시력의 결함을 교정하기 위한 안경의 시각 보조 도구로 사용됩니다.
역사
1758년 이후의 역사로 확장이 필요합니다.추가하면 도움이 됩니다. (2012년 1월) |

렌즈라는 단어는 렌틸 (렌틸 식물의 씨앗)의 라틴어 이름인 l ē어에서 왔는데, 이중 볼록 렌즈가 렌틸 모양이기 때문입니다.렌틸콩은 기하학적인 모양에 이름을 붙이기도 합니다.[a]
일부 학자들은 고고학적 증거가 수천 년에 걸쳐 고대에 렌즈의 광범위한 사용이 있었음을 나타낸다고 주장합니다.[1]이른바 님루드 렌즈는 기원전 7세기의 암석 결정 유물로, 확대경이나 불타는 유리로 사용되었을 수도, 사용되지 않았을 수도 있습니다.[2][3][4]다른 이들은 이집트 상형문자가 "단순한 유리 반수 렌즈"를 묘사한다고 주장합니다.[5][verification needed]
렌즈 사용에 대한 가장 오래된 언급은 아리스토파네스의 희곡 구름(기원전 424년)에서 불타는 유리를 언급한 것입니다.[6]대 플리니(1세기)는 불에 타는 안경이 로마 시대에 알려져 있었다는 것을 확인합니다.[7]플리니는 또한 네로가 에메랄드(근시를 교정하기 위해 오목한 것으로 추정됨)를 사용하여 검투 경기를 본다고 언급했을 때 교정 렌즈의 사용에 대해 알려진 최초의 언급을 가지고 있습니다.[8]플리니와 젊은 세네카 둘 다 물로 채워진 유리 지구본의 확대 효과를 묘사했습니다.
Ptolemy (2세기)는 광학에 관한 책을 썼는데, 그것은 불완전하고 매우 서투른 아랍어 번역의 라틴어로만 남아있습니다.그러나 이 책은 이슬람 세계의 중세 학자들이 받았고, 알하젠(Book of Optics, 11세기)에 의해 차례로 개선된 이븐 살(Ibn Sahl, 10세기)이 논평했습니다.프톨레마이오스 광학의 아랍어 번역은 12세기에 라틴어 번역으로 이용할 수 있게 되었습니다 (팔레르모의 에우제니우스 1154).11세기에서 13세기 사이에 "독서석"이 발명되었습니다.이것들은 처음에 유리구를 반으로 잘라 만든 원시적인 평면 볼록 렌즈였습니다.중세의 (11세기 또는 12세기) 암석 수정 비스비 렌즈는 타오르는 안경으로 사용하기 위한 것일 수도 있고 그렇지 않을 수도 있습니다.[9]
안경은 13세기 후반 북이탈리아에서 중세시대의 "독서석"을 개량한 것으로 발명되었습니다.[10]이는 안경 렌즈를 연마하고 연마하는 광학 산업의 시작으로, 처음에는 13세기 후반에 베네치아와 피렌체에서,[11] 나중에는 네덜란드와 독일의 안경 제조 센터에서 시작되었습니다.[12]안경 제작자들은 렌즈의 효과를 관찰함으로써 얻은 경험적 지식을 바탕으로 시력 교정을 위한 개선된 렌즈를 개발했습니다.[13][14]렌즈에 대한 실용적인 개발과 실험은 1595년 경 복합 광학 현미경의 발명으로 이어졌고, 1608년 굴절 망원경은 네덜란드의 안경 제작 센터에 등장했습니다.[15][16]
망원경과 현미경의 발명으로 렌즈에서 보이는 색 오차를 수정하려는 사람들에 의해 17세기와 18세기 초에 렌즈 모양에 대한 많은 실험이 있었습니다.안경사들은 다양한 형태의 곡률을 가진 렌즈를 제작하려고 했는데, 그들의 표면의 구면 모양의 결함으로 인해 오류가 발생했다고 잘못 가정했습니다.[17]굴절과 실험에 관한 광학 이론은 단일 요소 렌즈로는 모든 색상에 초점을 맞출 수 없다는 것을 보여주었습니다.이것은 1733년 영국의 체스터 무어 홀에 의한 복합 무채색 렌즈의 발명으로 이어졌는데, 이것은 또한 동료 영국인 존 돌런드가 1758년 특허로 주장한 발명품입니다.
단순 렌즈 제작
대부분의 렌즈는 구형 렌즈입니다: 두 표면은 구형 표면의 일부분입니다.각 면은 볼록(렌즈에서 바깥쪽으로 불룩), 오목(렌즈 안으로) 또는 평면(평면)일 수 있습니다.렌즈 표면을 구성하는 구의 중심을 이루는 선을 렌즈의 축이라고 합니다.일반적으로 렌즈 축은 제조 방식 때문에 렌즈의 물리적 중심을 통과합니다.렌즈는 다른 모양이나 크기를 제공하기 위해 제조 후 절단하거나 분쇄할 수 있습니다.그러면 렌즈 축이 렌즈의 물리적 중심을 통과하지 못할 수 있습니다.
토릭 또는 스페로 원통형 렌즈는 두 개의 직교 평면에서 두 개의 다른 곡률 반경을 갖는 표면을 갖습니다.그들은 각기 다른 경락에서 다른 초점력을 가지고 있습니다.이것은 난시 렌즈를 형성합니다.한 예로 누군가의 눈의 난시를 교정하기 위해 사용되는 안경 렌즈가 있습니다.
심플렌즈 종류

렌즈는 두 광학면의 곡률에 따라 분류됩니다.두 표면이 모두 볼록한 경우 렌즈는 이볼록(또는 이중 볼록, 또는 그냥 볼록)입니다.두 표면의 곡률반경이 동일한 경우 렌즈는 등볼록합니다.convex)입니다.두 개의 오목한 표면을 가진 렌즈는 쌍굴(또는 그냥 오목)입니다.한 표면이 평평한 경우 렌즈는 다른 표면의 곡률에 따라 평면 볼록 또는 평면 오목이 됩니다.한 쪽이 볼록하고 한 쪽이 오목한 렌즈는 볼록-오목 또는 반월상입니다.모양이 약간의 이상을 최소화하기 때문에 교정 렌즈에 가장 많이 사용되는 것이 바로 이런 종류의 렌즈입니다.
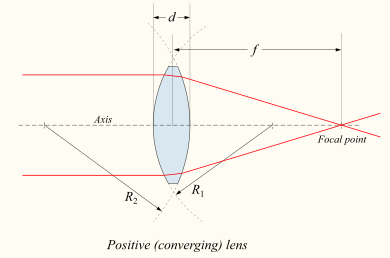
렌즈가 바이콘벡스 또는 플라노콘벡스인 경우 렌즈를 통과한 시준된 광선이 렌즈 뒤의 한 점(초점)으로 모입니다.이 경우, 렌즈는 포지티브 렌즈 또는 수렴 렌즈라고 불립니다.공기 중의 얇은 렌즈의 경우, 렌즈에서 스폿까지의 거리는 렌즈의 초점 거리이며, 이는 일반적으로 도표와 방정식 f로 표시됩니다.확장 반구형 렌즈는 특수한 유형의 평면 볼록 렌즈로, 렌즈의 곡면은 완전 반구형이고 렌즈는 곡률 반경보다 훨씬 두껍습니다.
두꺼운 볼록 렌즈의 또 다른 극단적인 경우는 볼 렌즈인데, 볼 렌즈의 모양은 완전히 둥글습니다.참신한 사진에 사용될 때 그것은 종종 "렌즈볼"이라고 불립니다.공 모양의 렌즈는 전방향성을 가진다는 장점이 있지만 대부분의 광학 글라스 유형의 경우 초점이 공의 표면에 가깝습니다. 렌즈 크기에 비해 공의 곡률이 극단적이기 때문에 색수차를 제외하고는 광학 수차가 얇은 렌즈보다 훨씬 더 좋지 않습니다.
 |  |
렌즈가 쌍각 또는 평면 오목인 경우 렌즈를 통과하는 시준 광선이 발산(확산)됩니다. 따라서 렌즈를 음각 또는 발산 렌즈라고 합니다.빔은 렌즈를 통과한 후 렌즈 앞 축의 특정 지점에서 뿜어져 나오는 것처럼 보입니다.공기 중의 얇은 렌즈의 경우, 이 지점에서 렌즈까지의 거리는 초점 거리이지만 수렴 렌즈의 초점 거리에 대해서는 음수입니다.
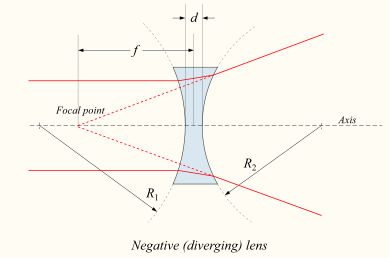 |  |

볼록 오목 렌즈(메니스커스)는 두 표면의 상대적인 곡률에 따라 양일 수도 있고 음일 수도 있습니다.음의 메니스커스 렌즈는 볼록한 표면보다 더 가파른 오목한 표면(볼록한 표면보다 더 짧은 반경)을 가지고 있으며 주변부보다 중앙부가 더 얇습니다.반대로 양의 메니스커스 렌즈는 볼록한 표면이 더 가파르고(오목한 표면보다 반지름이 더 짧은) 주변부보다 중앙부가 더 두껍습니다.
두 표면의 곡률이 같은 이상적인 얇은 렌즈는 광 파워가 0일 것이고, 이는 빛이 수렴하거나 발산하지 않는다는 것을 의미합니다.그러나 모든 실제 렌즈는 0이 아닌 두께를 가지고 있으므로 곡면이 동일한 실제 렌즈를 약간 긍정적으로 만듭니다.메니스커스 렌즈는 정확하게 0의 광학 전력을 얻기 위해 렌즈 두께의 영향을 고려하여 약간의 곡률이 동일하지 않아야 합니다.
구면의 경우
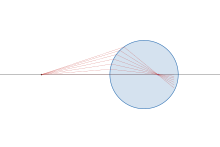
원 경계에 대한 단일 굴절의 경우, 객체와 이미지 사이의 관계는 다음과[18][19] 같이 주어집니다.
이것을 얇은 렌즈의 두 구면에 적용하면 렌즈 제조기의 공식이 됩니다.
파생
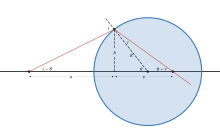
구면에 스넬의 법칙을 적용하면, = i =
도표에서도,
작은 각도 근사를 사용하고 i, r 및 θ를 제거하면,
렌즈메이커 방정식

공기 중 렌즈의 초점거리는 렌즈 제작자의 방정식으로 계산할 수 있습니다.[20]
어디에
- f는 렌즈의 초점거리입니다.
- n은 렌즈 재료의 굴절률이고,
- R은1 광원에 더 가까운 렌즈 표면의 곡률 반경(아래 참조)입니다.
- R은2 광원으로부터 멀리 떨어진 렌즈면의 곡률반경이며,
- d는 렌즈 두께(두 표면 정점 사이의 렌즈 축을 따라 거리)입니다.
초점 거리 f는 수렴 렌즈에 양수이고 발산 렌즈에는 음수입니다.초점 거리의 역수인 1/f는 렌즈의 광 파워입니다.초점 거리가 미터 단위인 경우, 이는 다이옵트레스(미터 단위) 단위의 광 파워를 제공합니다.
렌즈는 빛이 뒤쪽에서 앞쪽으로 이동할 때와 빛이 앞쪽에서 뒤쪽으로 이동할 때의 초점 거리가 같습니다.수차와 같은 렌즈의 다른 특성은 양쪽 방향에서 동일하지 않습니다.
곡률 반경 R과1 R에2 대한 부호 규약
렌즈의 곡률 반경의 부호는 해당 표면이 볼록한지 오목한지를 나타냅니다.이를 나타내기 위해 사용된 부호 규칙은 다양하지만, 이 문서에서 양의 R은 표면의 곡률 중심이 광선 이동 방향을 따라 더 멀리 있다는 것을 나타내는 반면, 음의 R은 표면에 도달한 광선이 이미 곡률 중심을 지나갔다는 것을 의미합니다.따라서, 상기 다이어그램과 같은 외부 렌즈 표면의 경우, R1 > 0 및 R < 0은 볼록한 표면(양의 렌즈에서 광을 수렴하는 데 사용됨)을 나타내고, R21 < 0 및s R > 0은 오목한 표면을 나타냅니다.곡률반경의 역수를 곡률이라고 합니다.평평한 표면은 곡률이 0이고, 곡률 반경은 무한합니다.
얇은 렌즈 근사
R과1 R에2 비해 d가 작으면 얇은 렌즈 근사가 가능합니다.공기중의 렌즈의 경우 f는 다음에 의해 주어집니다.
영상 속성
위에서 언급한 바와 같이 공기 중의 양극 또는 수렴 렌즈는 렌즈 축을 따라 이동하는 시준된 빔을 렌즈로부터 f 떨어진 지점(초점이라고 함)으로 포커싱합니다.반대로 초점에 배치된 광원은 렌즈에 의해 시준된 빔으로 변환됩니다.이 두 경우는 렌즈의 이미지 형성의 예입니다.전자의 경우 무한한 거리에 있는 물체(시준된 파동 빔으로 표시됨)는 렌즈의 초점에 있는 이미지로 초점이 맞춰집니다.후자에서는 렌즈로부터 초점거리 거리에 있는 물체를 무한대로 이미지화합니다.렌즈로부터 f 거리에 위치한 렌즈 축과 수직인 평면을 초점면이라고 합니다.
물체에서 렌즈까지의 거리와 렌즈에서 이미지까지의 거리가 각각 S와1 S일2 때, 두께가 무시할 수 있는 렌즈(얇은 렌즈)의 경우, 공기 중에서 거리는 얇은 렌즈 공식과 관계가 있습니다.[22][23][24]
이는 "뉴토니안" 형태로도 표현할 수 있습니다.
여기서 = S - } = 및 x = - } =

따라서 물체를 초점거리 f의 정렌즈로부터 S1 > f 거리에 두면 이 공식에 따라 영상거리 S를2 구할 수 있습니다.렌즈 반대쪽 S2 거리에 스크린을 두면 그 위에 이미지가 형성됩니다.이러한 이미지는 스크린 또는 이미지 센서에 투영될 수 있는 실제 이미지라고 합니다.이것이 카메라의 원리이며, 망막이 이미지 센서의 역할을 하는 인간의 눈의 원리이기도 합니다.
카메라의 초점 조절은 S를2 조절하는데, 이 공식에서 요구하는 것과 다른 이미지 거리를 사용하면 카메라로부터 S1 거리에 있는 물체에 대한 초점이 맞지 않는(퍼지) 이미지가 생성됩니다.다른 말로 하면, S를2 수정하면 다른 S에1 있는 물체가 완벽한 초점이 됩니다.

S가 음인2 경우도 있는데, 이는 이미지가 그러한 광선이 고려되는 렌즈의 반대쪽에 형성되어 있음을 나타냅니다.렌즈에서 발산되는 발산 광선은 결코 초점이 맞춰지지 않으며, 그러한 광선들은 물리적으로 상을 형성하는 것처럼 보이는 지점에 존재하지 않기 때문에, 이것은 가상 이미지라고 불립니다.실제 이미지와 달리 가상 이미지는 화면에 투사될 수 없고, 마치 가상 이미지가 있는 위치에 있는 실제 물체처럼 렌즈를 통해 보는 관찰자에게 나타납니다.마찬가지로 그 위치에 있는 물체처럼 후속 렌즈에 나타나서 두 번째 렌즈는 그 빛을 다시 실제 이미지로 초점을 맞출 수 있고, S는1 첫 번째 렌즈 뒤의 가상 이미지 위치에서 두 번째 렌즈로 측정됩니다.이것은 눈이 돋보기를 통해 볼 때 정확히 하는 일입니다.돋보기는 돋보기 뒤에 가상 이미지를 생성하지만, 그 광선들은 망막에 실제 이미지를 만들기 위해 눈의 렌즈에 의해 다시 이미지화됩니다.
초점 거리 f의 양의 렌즈를 사용하면 S1 < f, 따라서 렌즈가 확대경으로 사용될 때 (S1 > > > 가 아닌 카메라로 사용될 때) 가상 이미지가 생성됩니다.상기 식에 따르면, 실제 물체(S1 > 0)를 갖는 네거티브 렌즈(f < 0)를 사용하는 것은 허상2(S < 0)만을 생성할 수 있습니다.물체 거리 S가1 음수일 수도 있는데, 이 경우 렌즈는 소위 가상 물체를 봅니다.이것은 렌즈가 실제 이미지의 위치 이전에 수렴하는 빔(이전 렌즈에 의해 초점이 맞춰짐)에 삽입될 때 발생합니다.그런 경우에는 마이너스 렌즈라도 바로우 렌즈처럼 실제 영상을 투사할 수 있습니다.
얇은 렌즈의 경우, S와12 S의 거리는 상술한 바와 같이 물체와 이미지로부터 렌즈의 위치까지 측정됩니다.렌즈의 두께가 S와1 S보다2 작지 않거나 렌즈 요소(복합 렌즈)가 여러 개일 경우, 대신 물체와 이미지에서 렌즈의 주 평면까지 측정해야 합니다.거리 S1 또는 S가2 공기 또는 진공 이외의 매질을 통과할 경우에는 보다 복잡한 분석이 필요합니다.
확대
단일 렌즈를 사용하는 이미징 시스템의 선형 확대는 다음과 같이 제공됩니다.
여기서 M은 객체의 크기와 비교하여 이미지의 크기의 비율로 정의된 확대 계수입니다.여기서 부호 규칙은 실제 이미지의 경우와 마찬가지로 M이 음수이면 이미지가 개체에 대해 거꾸로 표시된다는 것을 지시합니다.가상 이미지의 경우 M이 양수이므로 이미지가 직립합니다.
이 확대 공식은 수렴 렌즈(f > 0)와 발산 렌즈(f < 0)를 구별하는 두 가지 쉬운 방법을 제공합니다.렌즈에 매우 가까운 물체(0 < S1 < f)의 경우 수렴 렌즈는 확대(더 큰) 가상 이미지를 형성하고 발산 렌즈는 축소(더 작은) 이미지를 형성합니다. 렌즈에서 매우 먼 물체(S1 > f > 0)의 경우 수렴 렌즈는 반전 이미지를 형성하고 발산 렌즈는 직립 이미지를 형성합니다.
선형 확대 M이 항상 확대력의 가장 유용한 척도는 아닙니다.예를 들어, 가상 이미지만 생성하는 시각 망원경이나 쌍안경을 특성화할 때, 사람들은 망원경을 통해 멀리 있는 물체가 육안에 비해 얼마나 더 크게 보이는지를 나타내는 각도 배율에 더 관심을 가질 것입니다.카메라의 경우 플레이트 스케일을 인용할 수 있는데, 플레이트 스케일은 멀리 있는 물체의 겉보기(각형) 크기와 초점에서 생성된 실제 이미지의 크기를 비교합니다.플레이트 스케일은 카메라 렌즈의 초점 거리의 역수이며, 렌즈는 초점 거리에 따라 장초점 렌즈 또는 광각 렌즈로 분류됩니다.
부적절한 배율 측정을 사용하면 형식적으로는 정확하지만 의미 없는 수치를 얻을 수 있습니다.예를 들어, 눈에서 20cm, 물체에서 5cm 떨어진 곳에서 초점 거리 5cm의 돋보기를 사용하여 무한한 선형 크기의 가상 이미지를 생성합니다.M = ∞. 하지만 각진 배율이 5. 즉, 렌즈가 없을 때보다 눈에 5배나 큰 물체가 나타난다는 것을 의미합니다.50 mm 렌즈의 카메라를 사용하여 달을 촬영할 때, 선형 배율 M ≈ -50 mm / 380000 km = -1.3 x 10에 상관이 없습니다.오히려 카메라의 플레이트 스케일은 약 1°/mm이고, 이로부터 필름에 있는 0.5mm 이미지는 지구에서 볼 수 있는 달의 각도 크기 약 0.5°에 해당한다고 결론을 내릴 수 있습니다.
물체가 무한히 멀리 떨어져 있는 극단적인 경우에는 S = ∞, S = f 및 M = -f/ ∞ = 0으로 초점면의 단일 지점으로 물체가 이미지화됨을 나타냅니다.사실, 회절은 점 퍼짐 함수의 크기에 더 낮은 제한을 두기 때문에 투영된 점의 지름은 실제로 0이 아닙니다.이것을 회절 한계라고 합니다.

수차
| 광수차 |
|---|
렌즈는 완벽한 이미지를 형성하지 않으며, 렌즈는 항상 이미지를 물체의 불완전한 복제품으로 만드는 어느 정도의 왜곡이나 수차를 발생시킵니다.특정 용도의 렌즈 시스템을 세심하게 설계하면 수차를 최소화할 수 있습니다.구면 수차, 혼수 및 색수차를 포함한 여러 유형의 수차가 화질에 영향을 미칩니다.
구면 수차
구면 수차는 구면이 렌즈에 이상적인 모양은 아니지만 유리를 갈아서 연마할 수 있는 가장 단순한 모양이기 때문에 자주 사용됩니다.구면 수차로 인해 렌즈 축과 평행하지만 거리가 먼 빔은 축에 가까운 빔과 약간 다른 위치에 초점이 맞춰집니다.이는 이미지의 흐릿함으로 나타납니다.구면 수차는 일반 렌즈 모양으로 특정 용도의 표면 곡률을 신중하게 선택하여 최소화할 수 있습니다.예를 들어, 시준된 빔의 초점을 맞추기 위해 사용되는 평면 볼록 렌즈는 빔 소스를 향해 볼록한 면과 함께 사용될 때 더 날카로운 초점 지점을 생성합니다.
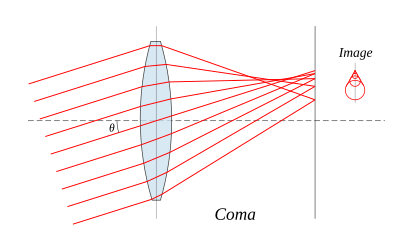
혼수상태
혼수상태, 또는 혼수상태의 수차는 그 이름이 수차된 이미지의 혜성 같은 모습에서 유래되었습니다.혼수상태는 렌즈의 광축에서 벗어난 물체가 이미지화될 때 발생하며, 여기서 광선은 렌즈를 축 θ으로 비스듬히 통과합니다.초점 거리 f의 렌즈 중심을 통과하는 광선은 축에서 θ 거리 f의 한 지점에 집중됩니다.렌즈의 바깥쪽 가장자리를 통과하는 광선은 축에서 더 멀리(양의 혼수 상태) 또는 축에 더 가깝게(음의 혼수 상태) 다른 지점에 초점이 맞춰집니다.일반적으로, 렌즈의 중심으로부터 일정한 거리를 두고 렌즈를 통과하는 평행선 다발은, 코마틱 서클(comatic circle)이라고 하는, 초점면의 링 형상의 화상으로 포커싱됩니다.이 모든 원들의 합은 V 모양이나 혜성과 같은 플레어로 이어집니다.구면 수차와 마찬가지로, 두 렌즈 표면의 곡률을 응용 프로그램과 일치시킬 수 있도록 선택함으로써 혼수 상태를 최소화할 수 있습니다.구면 수차와 혼수가 모두 최소화된 렌즈를 베스트 폼 렌즈라고 합니다.
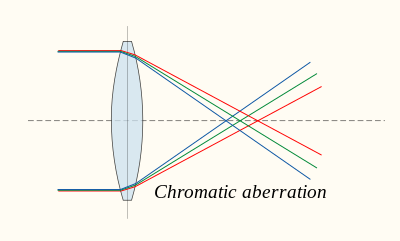
색수차
색수차는 빛의 파장에 따른 굴절률 n의 변화인 렌즈 재료의 분산에 의해 발생합니다.위의 공식들로부터, f는 n에 의존하기 때문에, 다른 파장의 빛이 다른 위치로 초점이 맞춰지는 것을 따릅니다.렌즈의 색수차는 이미지 주변에 있는 색상의 테두리로 보입니다.분산이 다른 두 물질을 결합하여 하나의 렌즈를 형성하는 무채색 더블렛(또는 무채색)을 사용하여 최소화할 수 있습니다.이것은 완벽한 보정을 생성하지는 않지만 특정 파장 범위에서 색수차의 양을 줄입니다.무채색의 사용은 광학 현미경의 발전에 있어서 중요한 단계였습니다.아포크로마트(apochromat)는 구면 수차 보정이 개선된 렌즈 또는 렌즈 시스템입니다.아포크로마토는 무채색 보다 훨씬 더 비쌉니다.
특수 코팅 또는 수정 불소로 만든 렌즈와 같이 색수차를 최소화하기 위해 다양한 렌즈 재료를 사용할 수도 있습니다.이 자연적으로 발생하는 물질은 아베수가 가장 높게 알려져 있고, 이것은 그 물질이 낮은 산포를 가지고 있음을 나타냅니다.
기타 유형의 수차
다른 종류의 수차에는 장 곡률, 배럴 및 핀쿠션 왜곡 및 난시가 포함됩니다.
조리개 회절
상기와 같은 수차를 최소화하거나 제거하도록 렌즈를 설계하더라도 렌즈의 유한개구를 통과하는 빛의 회절에 의해 화질이 여전히 제한됩니다.회절 제한 렌즈(diffraction-limited lens)는 설계 조건에서 주로 회절에 의해 화질이 제한될 정도로 수차가 감소된 렌즈입니다.
컴파운드렌즈
단순 렌즈는 위에서 설명한 광학적 이상에 따라 달라집니다.많은 경우 이러한 이상은 보완적인 이상이 있는 간단한 렌즈를 사용하여 상당한 정도로 보상될 수 있습니다.컴파운드 렌즈는 서로 다른 모양의 단순한 렌즈들의 집합체이며 굴절률이 서로 다른 물질들로 만들어져 있으며, 서로 같은 축으로 배열되어 있습니다.
가장 간단한 경우는 렌즈가 접촉하는 경우입니다: 초점 거리 f와1 f의2 렌즈가 "얇다"면 렌즈의 결합 초점 거리 f는 다음과 같습니다.
1/f가 렌즈의 힘이기 때문에 접촉하는 얇은 렌즈의 힘이 첨가되어 있음을 알 수 있습니다.
두 개의 얇은 렌즈가 공기 중에서 어느 정도 거리 d만큼 떨어져 있다면, 결합된 시스템에 대한 초점 거리는 다음과 같습니다.
결합된 렌즈의 전방 초점에서 첫 번째 렌즈까지의 거리를 전방 초점 거리(FFL)라고 합니다.
마찬가지로, 두 번째 렌즈에서 결합된 시스템의 후방 초점까지의 거리는 후방 초점 거리(BFL)입니다.
d가 0인 경향이 있으므로 초점 거리는 접촉하는 얇은 렌즈에 대해 주어진 f 값을 가지는 경향이 있습니다.
이격 거리가 초점 거리의 합과 같으면(d = f + f), FFL 및 BFL은 무한대입니다.이는 평행(시준) 빔을 다른 시준 빔으로 변환하는 한 쌍의 렌즈에 해당합니다.이 유형의 시스템은 빔의 순 수렴 또는 발산을 생성하지 않기 때문에 초점 시스템이라고 불립니다.이 분리에 있는 두 개의 렌즈는 가장 간단한 형태의 광학 망원경을 형성합니다.시스템이 시준된 빔의 발산을 변경하지는 않지만 빔의 폭을 변경합니다.그러한 망원경의 배율은 다음과 같이 주어집니다.
출력 빔 폭과 입력 빔 폭의 비율입니다.부호 규칙에 주목하십시오. 두 개의 볼록 렌즈(f1 > 0, f > 02)가 있는 망원경은 음의 배율을 생성하여 반전된 이미지를 나타냅니다.볼록한 렌즈와 오목한 렌즈(f1 > 0 > f2)는 양의 배율을 생성하고 이미지는 직립합니다.간단한 광학 망원경에 대한 자세한 내용은 굴절 망원경 § 굴절 망원경 설계를 참조하십시오.
비구형

원통형 렌즈는 한 축만을 따라 곡률을 갖습니다.그것들은 빛을 선으로 초점을 맞추거나 레이저 다이오드의 타원형 빛을 둥근 빔으로 변환하는 데 사용됩니다.그들은 또한 영화 아나모픽 렌즈에 사용됩니다.
비구면 렌즈는 구형도 원통형도 아닌 적어도 하나의 표면을 가지고 있습니다.더 복잡한 모양은 그러한 렌즈가 표준 단순 렌즈보다 더 적은 수차로 이미지를 형성할 수 있게 해주지만, 그것들을 만드는 것은 더 어렵고 비용이 많이 듭니다.이것들은 예전에는 만들기가 복잡하고 종종 엄청나게 비쌌지만, 기술의 발전은 그러한 렌즈의 제조 비용을 크게 감소시켰습니다.

프레넬 렌즈는 광학 표면이 좁은 고리로 나뉘어서 기존의 렌즈보다 훨씬 얇고 가벼워질 수 있습니다.내구성이 좋은 프레넬 렌즈는 플라스틱으로 성형할 수 있고 가격도 저렴합니다.
렌티큘러 렌즈(Lenticular lens)는 렌티큘러 인쇄에 사용되는 마이크로 렌즈의 배열로, 깊이에 대한 환상을 갖거나 다른 각도에서 볼 때 이미지가 변합니다.
이중 초점 렌즈는 렌즈에 접지된 두 개 이상의 초점 거리 또는 눈금이 있습니다.
그래디언트 인덱스 렌즈는 평평한 광학 표면을 가지고 있지만 렌즈를 통과하는 빛이 초점을 이루게 하는 굴절률의 반경 또는 축 방향 변화를 가지고 있습니다.
액시콘은 원뿔모양의 광학면을 가지고 있습니다.점 소스를 광축을 따라 선으로 이미징하거나 레이저 빔을 링으로 변환합니다.[28]
회절 광학 요소는 렌즈로 작동할 수 있습니다.
슈퍼렌즈는 음의 지수 메타물질로 만들어지며 회절 한계를 초과하는 공간 해상도로 이미지를 생성한다고 주장합니다.[29]첫 번째 슈퍼렌즈는 2004년에 마이크로웨이브를 위한 메타물질을 사용하여 만들어졌습니다.[29]다른 연구자들에 의해 개선된 버전이 만들어졌습니다.[30][31]2014년[update] 현재 슈퍼렌즈는 가시광선 또는 근적외선 파장에서 아직 입증되지 않았습니다.[32]
곡률이 없는 평평한 초박형 렌즈가 개발되었습니다.[33]
사용하다

손잡이나 스탠드가 있는 프레임에 장착된 단일 볼록 렌즈는 돋보기입니다.
렌즈는 근시, 고메트로피아, 노안, 난시 등의 굴절 오류 교정을 위한 보철로 사용됩니다.(교정렌즈, 콘택트렌즈, 안경, 안구내렌즈 참조)다른 용도로 사용되는 대부분의 렌즈는 엄격한 축대칭성을 갖지만 안경 렌즈는 대략적으로 대칭성을 갖습니다.이들은 보통 원형이 아닌 대략 타원형의 틀에 맞도록 모양을 만듭니다. 광학 중심은 안구 위에 배치됩니다. 이들의 곡률은 난시를 교정하기 위해 축방향으로 대칭되지 않을 수 있습니다.선글라스의 렌즈는 빛을 감쇠시키도록 설계되었으며 시각 장애를 교정하는 선글라스 렌즈도 맞춤 제작할 수 있습니다.
다른 용도는 단안, 쌍안경, 망원경, 현미경, 카메라, 프로젝터와 같은 영상 시스템에 있습니다.이러한 기구들 중 일부는 사람의 눈에 적용될 때 가상 이미지를 생성합니다. 다른 기구들은 사진 필름이나 광학 센서에 포착되거나 화면에서 볼 수 있는 실제 이미지를 생성합니다.이러한 장치에서 렌즈는 때때로 곡선 미러와 짝을 이루어 렌즈의 구면 수차가 미러의 반대 수차를 보정하는 Catadioptric 시스템을 만듭니다(예: Schmidt 및 meniscus corrector).
볼록 렌즈는 초점이 무한대인 물체의 이미지를 생성합니다. 태양이 이미지화되면 렌즈에 입사된 가시광선과 적외선의 많은 부분이 작은 이미지로 집중됩니다.큰 렌즈는 인화성 물체를 초점에서 태울 수 있을 정도의 강도를 만듭니다.제대로 제작되지 않은 렌즈로도 점화가 가능하기 때문에 렌즈는 최소 2400년 동안 불에 타는 안경으로 사용되어 왔습니다.[6]현대적인 응용은 태양 에너지를 상대적으로 작은 태양광 전지에 집중시키기 위해 비교적 큰 렌즈를 사용하는 것으로, 더 크고 더 비싼 전지를 사용할 필요 없이 더 많은 에너지를 수확합니다.
전파천문학과 레이더 시스템은 전자기 방사선을 수집기 안테나로 굴절시키기 위해 흔히 렌즈 안테나라고 불리는 유전체 렌즈를 자주 사용합니다.
렌즈가 긁히고 닳을 수 있습니다.이를 제어하기 위해 내마모성 코팅을 사용할 수 있습니다.[34]
참고 항목
메모들
- ^ 변형 맞춤법 렌즈가 가끔 보입니다.일부 사전에서는 대체 철자로 나열되지만, 대부분의 주류 사전에서는 허용되는 철자로 나열되지 않습니다.
- Brians, Paul (2003). Common Errors in English. Franklin, Beedle & Associates. p. 125. ISBN 978-1-887902-89-2. Retrieved 28 June 2009. 일부 사전에 나열된 것처럼 "렌즈"를 보고하지만 일반적으로 허용되는 것으로 간주되지는 않습니다.
- Merriam-Webster's Medical Dictionary. Merriam-Webster. 1995. p. 368. ISBN 978-0-87779-914-6. "렌즈"를 허용 가능한 대체 철자로 나열합니다.
- "Lens or Lense – Which is Correct?". writingexplained.org. 30 April 2017. 거의 무시할 수 있는 사용 빈도를 분석하여 철자 오류가 복수(렌즈)의 잘못된 단수화의 결과라는 결론을 내립니다.
참고문헌
- ^ Sines, George; Sakellarakis, Yannis A. (1987). "Lenses in antiquity". American Journal of Archaeology. 91 (2): 191–196. doi:10.2307/505216. JSTOR 505216. S2CID 191384703.
- ^ Whitehouse, David (1 July 1999). "World's oldest telescope?". BBC News. Archived from the original on 1 February 2009. Retrieved 10 May 2008.
- ^ "The Nimrud lens/The Layard lens". Collection database. The British Museum. Archived from the original on 19 October 2012. Retrieved 25 November 2012.
- ^ D. Brewster (1852). "On an account of a rock-crystal lens and decomposed glass found in Niniveh". Die Fortschritte der Physik (in German). Deutsche Physikalische Gesellschaft. p. 355.
- ^ Kriss, Timothy C.; Kriss, Vesna Martich (April 1998). "History of the Operating Microscope: From Magnifying Glass to Microneurosurgery". Neurosurgery. 42 (4): 899–907. doi:10.1097/00006123-199804000-00116. PMID 9574655.
- ^ a b Aristophanes (22 January 2013) [First performed in 423 BC]. The Clouds. Translated by Hickie, William James. Project Gutenberg. EBook #2562.[2017년 6월 28일 Wayback Machine에서 Aristophanes (22 January 2013) [First performed in 423 BC]. The Clouds. Translated by Hickie, William James. Project Gutenberg. EBook #2562.보관됨
- ^ 대 플리니, 자연사 (트랜스)John Bostock) Book XXXVII, Chap. 10 Wayback Machine에서 2008년 10월 4일 보관.
- ^ 대 플리니, 자연사 (트랜스)John Bostock) Book XXXVII, Chap. 16 2008년 9월 28일 Wayback Machine에서 보관
- ^ Tilton, Buck (2005). The Complete Book of Fire: Building Campfires for Warmth, Light, Cooking, and Survival. Menasha Ridge Press. p. 25. ISBN 978-0-89732-633-9.
- ^ Glick, Thomas F.; Steven John Livesey; Faith Wallis (2005). Medieval science, technology, and medicine: an encyclopedia. Routledge. p. 167. ISBN 978-0-415-96930-7. Archived from the original on 20 January 2023. Retrieved 24 April 2011.
- ^ 알 반 헬든.갈릴레오 프로젝트 > 과학 > 망원경 2004년 6월 23일 웨이백 머신에서 보관.Galileo.rice.edu .2012년 6월 6일 회수.
- ^ Henry C. King (28 September 2003). The History of the Telescope. Courier Dover Publications. p. 27. ISBN 978-0-486-43265-6. Archived from the original on 2 July 2023. Retrieved 6 June 2012.
- ^ Paul S. Agutter; Denys N. Wheatley (12 December 2008). Thinking about Life: The History and Philosophy of Biology and Other Sciences. Springer. p. 17. ISBN 978-1-4020-8865-0. Retrieved 6 June 2012.
- ^ Vincent Ilardi (2007). Renaissance Vision from Spectacles to Telescopes. American Philosophical Society. p. 210. ISBN 978-0-87169-259-7. Retrieved 6 June 2012.[영구 데드링크]
- ^ 현미경: 타임라인 2010년 1월 9일 노벨 재단 웨이백 머신에서 보관.2009년 4월 3일 회수
- ^ Fred Watson (1 October 2007). Stargazer: The Life and Times of the Telescope. Allen & Unwin. p. 55. ISBN 978-1-74175-383-7. Retrieved 6 June 2012.
- ^ 이 단락은 브리태니커 백과사전의 1888년판 æ에서 발췌한 것입니다.
- ^ "4.4: Spherical Refractors". Physics LibreTexts. 2 July 2019. Archived from the original on 26 November 2022. Retrieved 2 July 2023.
- ^ "Refraction at Spherical Surfaces". personal.math.ubc.ca. Archived from the original on 26 October 2021. Retrieved 2 July 2023.
- ^ Greivenkamp 2004, 페이지 14
Hecht 1987, § 6.1 - ^ Hecht 1987, § 5.2.3.
- ^ Nave, Carl R. "Thin Lens Equation". Hyperphysics. Georgia State University. Archived from the original on 12 October 2000. Retrieved 17 March 2015.
- ^ Colwell, Catharine H. "Resource Lesson: Thin Lens Equation". PhysicsLab.org. Archived from the original on 2 April 2015. Retrieved 17 March 2015.
- ^ "The Mathematics of Lenses". The Physics Classroom. Archived from the original on 10 March 2015. Retrieved 17 March 2015.
- ^ Hecht 2002, p. 120.
- ^ 항상 3개의 "쉬운 광선"이 있습니다.이 경우 세 번째 광선에 대해서는 파일을 참조하십시오.렌즈3b 3차 광선.svg
- ^ Hecht 2002, p. 168.
- ^ Proteep Mallik (2005). "The Axicon" (PDF). Archived from the original (PDF) on 23 November 2009. Retrieved 22 November 2007.
- ^ a b Grbic, A.; Eleftheriades, G. V. (2004). "Overcoming the Diffraction Limit with a Planar Left-handed Transmission-line Lens". Physical Review Letters. 92 (11): 117403. Bibcode:2004PhRvL..92k7403G. doi:10.1103/PhysRevLett.92.117403. PMID 15089166.
- ^ Valentine, J.; et al. (2008). "Three-dimensional optical metamaterial with a negative refractive index". Nature. 455 (7211): 376–9. Bibcode:2008Natur.455..376V. doi:10.1038/nature07247. PMID 18690249. S2CID 4314138.
- ^ Yao, Jie; Liu, Zhaowei; Liu, Yongmin; Wang, Yuan; Sun, Cheng; Bartal, Guy; Stacy, Angelica M.; Zhang, Xiang (15 August 2008). "Optical Negative Refraction in Bulk Metamaterials of Nanowires". Science. 321 (5891): 930. Bibcode:2008Sci...321..930Y. CiteSeerX 10.1.1.716.4426. doi:10.1126/science.1157566. ISSN 0036-8075. PMID 18703734. S2CID 20978013.
- ^ Nielsen, R.B.; Thoreson, M.D.; Chen, W.; Kristensen, A.; Hvam, J.M.; Shalaev, V. M.; Boltasseva, A. (2010). "Toward superlensing with metal–dielectric composites and multilayers" (PDF). Applied Physics B. 100 (1): 93. Bibcode:2010ApPhB.100...93N. doi:10.1007/s00340-010-4065-z. S2CID 39903291. Archived from the original (PDF) on 9 March 2013.
- ^ Patel, Prachi (2015). "Good-Bye to Curved Lens: New Lens Is Flat". Scientific American. 312 (5): 22. doi:10.1038/scientificamerican0515-22b. PMID 26336702. Archived from the original on 19 May 2015. Retrieved 16 May 2015.
- ^ Schottner, G (May 2003). "Scratch and Abrasion Resistant Coatings on Plastic Lenses—State of the Art, Current Developments and Perspectives". Journal of Sol-Gel Science and Technology. Vol. 27. pp. 71–79. doi:10.1023/A:1022684011222.
서지학
- Hecht, Eugene (1987). Optics (2nd ed.). Addison Wesley. ISBN 978-0-201-11609-0. 5장과 6장.
- Hecht, Eugene (2002). Optics (4th ed.). Addison Wesley. ISBN 978-0-321-18878-6.
- Greivenkamp, John E. (2004). Field Guide to Geometrical Optics. SPIE Field Guides vol. FG01. SPIE. ISBN 978-0-8194-5294-8.
외부 링크
- 굴절과 렌즈에 관한 온라인 교과서의 한 장 2009년 12월 17일 Wayback Machine에서 보관.
- Project PhysNET의 얇은 구면 렌즈(.pdf).
- 렌즈 기사(digitalartform.com )
- 고대 이집트의 렌즈에 관한 글
- 볼록렌즈를 통한 전자파 전파를 이용한 유튜브 FDTD 애니메이션
- 고전세계에서 확대렌즈의 사용
- Henker, Otto (1911). . Encyclopædia Britannica. Vol. 16 (11th ed.). pp. 421–427. (21개 다이어그램 포함)
시뮬레이션
- 시뮬레이션을 통한 학습 – 오목 및 볼록 렌즈
- OpticalRayTracer – 오픈 소스 렌즈 시뮬레이터(다운로드 가능한 Java)
- QED에 의한 렌즈 시연 애니메이션




![{\displaystyle {\frac {1}{\ f\ }}=(n-1)\left[{\frac {1}{\ R_{1}\ }}-{\frac {1}{\ R_{2}\ }}+{\frac {\ (n-1)\ d\ }{n\ R_{1}R_{2}}}\right]\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b0e6ff8a2db86e343f9d0a8d03775c8863b3fba)
![{\displaystyle {\frac {1}{\ f\ }}\approx \left(n-1\right)\left[{\frac {1}{\ R_{1}\ }}-{\frac {1}{\ R_{2}\ }}\right]~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b89ddca06d3280a0e4061d4df4d128346d6310cc)