루네부르크 렌즈
Luneburg lens루네부르크 렌즈(원래 독일 뤼네부르크 렌즈, 때때로 철자가 잘못 표기된 루네베르크 렌즈)는 spherically 대칭 구배 지수 렌즈다. 전형적인 루네부르크 렌즈의 굴절률 n은 중심에서 바깥 표면으로 방사상으로 감소한다. 그것들은 가시광선에서 전파에 이르는 전자기 방사선과 함께 사용될 수 있다.
특정 인덱스 프로파일의 경우 렌즈는 주어진 두 개의 동심원의 완벽한 기하학적 이미지를 서로 형성할 것이다. 이러한 효과를 발생시킬 수 있는 굴절 지수 프로파일이 무한히 많다. 가장 간단한 해결책은 1944년 루돌프 루네부르크에 의해 제안되었다.[1] 굴절률에 대한 루네부르크의 솔루션은 렌즈 외부에 두 개의 결합 포커스를 만든다. 하나의 초점이 무한대에 놓여 있고, 다른 초점은 렌즈의 반대쪽 표면에 놓여 있다면, 해결책은 간단하고 명시적인 형태를 취한다. 이후 J. Brown과 A. S. Gutman은 하나의 내부 초점과 하나의 외부 초점을 생성하는 해결책을 제안했다.[2][3] 이러한 솔루션은 고유하지 않다. 솔루션 세트는 숫자로 평가되어야 하는 일련의 명확한 통합에 의해 정의된다.[4]
디자인
루네부르크의 해결책
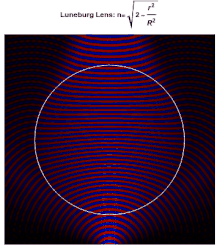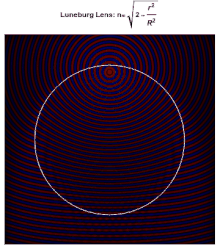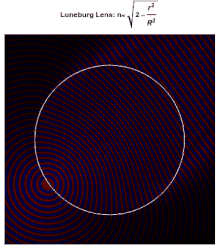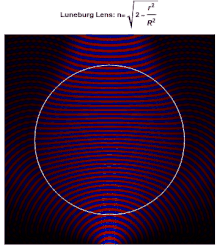
이상적인 루네부르크 렌즈의 표면의 각 지점은 반대편의 병렬 방사선 사고를 위한 초점이다. 이상적으로는 렌즈를 구성하는 재료의 유전체 상수 r 이(가) 중심에서 표면에서 2로(또는 동등하게, n 이(가) 에서 1로)로 떨어진다고 한다.
여기서 은(는) 렌즈의 반지름이다. 표면의 굴절률이 주변 매체의 굴절률과 같기 때문에 표면에서는 반사가 일어나지 않는다. 렌즈 안에서, 광선의 경로는 타원의 호이다.
맥스웰 어안 렌즈
맥스웰의 어안렌즈도 일반화된 루네부르크 렌즈의 예다. 1854년[5] 맥스웰이 처음으로 충분히 설명한 어안(따라서 루네부르크의 솔루션을 미리 예약)은 에 따라 굴절률이 달라진다.
그것은 반지름 R의 구면 표면에 각 점을 동일한 표면의 반대 지점에 집중시킨다. 렌즈 안에서는 광선의 경로가 원호형이다.
발행 및 귀속
이 렌즈의 특성은 1853년 캠브리지와 더블린 수학 저널의 여러 세트 문제나 퍼즐 중 하나에 설명되어 있다.[6] 광선이 원형 경로를 묘사하고 있다는 점에서 반경의 함수로서 굴절 지수를 찾고, 나아가 렌즈의 초점 특성을 입증하는 것이 과제다. 그 해결책은 같은 저널의 1854년 판에 제시되어 있다.[5] 그 문제들과 해결책들은 원래 익명으로 출판되었지만, 이 문제의 해결책(그리고 다른 한 가지)은 맥스웰이 죽은 지 11년 만에 출판된 니벤의 <제임스 서클 맥스웰의 과학논문>에 수록되어 있었다.[7]
적용들
실제로 루네부르크 렌즈는 일반적으로 각 굴절률의 다른 각 다른 굴절률로 분리된 동심 쉘의 층을 이루는 구조물이다. 이 셸들은 루네부르크의 솔루션과는 약간 다른 계단식 굴절률 프로파일을 형성한다. 이러한 종류의 렌즈는 주로 마이크로파 주파수에 사용되며, 특히 효율적인 마이크로파 안테나와 레이더 보정 표준을 구축하기 위해 사용된다. 루네부르크 렌즈의 원통형 아날로그는 레이저 다이오드의 빛을 시준하는 데도 사용된다.
레이더 반사기
레이더 반사기는 표면의 일부를 야금화하여 뤼네부르크 렌즈로 만들 수 있다. 원거리 레이더 송신기의 방사선은 렌즈 반대편의 야금화 밑면에 집중된다. 여기서 반사되어 레이더 스테이션에 다시 집중된다. 이 계획의 난점은 야금화된 지역이 수정체의 그 부분에 방사선의 진입이나 출구를 차단하지만, 비금속화된 영역은 반대편에 사각지대가 생긴다는 것이다.
훈련 작전 중 스텔스 항공기가 보이도록 하거나, 실제 레이더 시그니처를 감추기 위해 이동식 루네부르크 렌즈형 레이더 반사체를 군용 항공기에 부착하는 경우도 있다. 다른 종류의 레이더 반사기와는 달리, 그 모양은 항공기의 취급에 영향을 주지 않는다.[8]
마이크로파 안테나
루네부르크 렌즈는 고게인 라디오 안테나의 기초로 사용될 수 있다. 이 안테나는 접시 안테나에 견줄 만하지만 포물선 반사체보다는 렌즈를 주 초점 요소로 사용한다. 디시 안테나와 마찬가지로 수신기 또는 송신기에서 공급되는 피드는 일반적으로 경음기 안테나로 구성되는 포커스에 위치한다. 공급 경음기의 위상 중심은 초점점과 일치해야 하지만 위상 중심은 항상 경음기 입구의 어느 정도 내부에 있기 때문에 렌즈 표면에 대고 바로 위로 들어올릴 수 없다. 따라서 표면에 포커스가 놓여 있는 고전적인 렌즈보다는 [9]표면 너머에 다소 초점을 맞춘 다양한 루네부르크 렌즈를 사용할 필요가 있다.
루네부르크 렌즈 안테나는 포물선 접시보다 많은 장점을 제공한다. 렌즈가 수직 대칭이기 때문에 안테나는 전체 안테나를 회전할 필요 없이 렌즈 주위로 피드를 이동시켜 조향할 수 있다. 다시 말하지만, 렌즈가 세로로 대칭적이기 때문에, 하나의 렌즈를 사용할 수 있고, 여러 피드가 서로 다른 방향을 볼 수 있다. 이와는 대조적으로 포물선 반사기와 함께 복수의 피드를 사용하는 경우 혼수상태(비집중성의 한 형태)를 겪지 않도록 모두 광축의 작은 각도 안에 있어야 한다. 오프셋 시스템을 제외하고, 접시 안테나는 공급과 그것의 지지 구조로 인해 주 요소를 부분적으로 가린다(부착 차단). 다른 굴절 시스템과 마찬가지로 루네부르크 렌즈 안테나는 이러한 문제를 방지한다.
뤼네부르크 렌즈 안테나의 변화는 반구형 뤼네부르크 렌즈 안테나 또는 뤼네부르크 반사 안테나다. 이것은 루네부르크 렌즈의 반구 하나만 사용하며 구의 절단면은 반사 금속 지면에 놓인다. 배열은 렌즈 무게의 반을 차지하며, 지상면은 편리한 지지 수단을 제공한다. 그러나 반사경의 입사각이 약 45° 미만이면 사료는 부분적으로 렌즈를 흐리게 한다.
렌즈 내 광선 경로
모든 수직 대칭 렌즈의 경우, 각 레이는 전적으로 렌즈 중심을 통과하는 평면에 놓여 있다. 광선의 초기 방향은 렌즈의 중심점과 함께 렌즈를 이등분하는 평면을 식별하는 선을 정의한다. 렌즈의 대칭면으로서 굴절률의 구배는 이 평면에 수직으로 작용하여 광선이 그 한쪽 또는 다른 쪽으로 편차를 일으키지 않는다. 평면에서는 시스템의 원형 대칭으로 극좌표 ,을 사용하여 레이의 궤적을 묘사하는 것이 편리하다.
광선의 어떤 두 지점(렌즈의 입구와 출구의 지점 등)을 감안할 때, 페르마의 원칙은 광선이 그들 사이를 이동하는 경로가 가능한 최소 시간 내에 통과할 수 있는 경로라고 주장한다. 렌즈의 어느 지점에서든 빛의 속도가 굴절률에 반비례하고, 피타고라스에 의해 두 지점 1,1 ) 과 2, ){\ 사이의 전달 시간이 된다.
여기서 은(는) 진공에서 빛의 속도다. 이 을(를) 최소화하면 광선 경로를 따라 에 대한 의 의존도를 결정하는 2차 미분 방정식이 생성된다. 이러한 유형의 최소화 문제는 라그랑기 역학에서 광범위하게 연구되어 왔으며, 이 2차 방정식의 첫 번째 적분을 즉시 공급하는 벨트라미 정체성의 형태로 기성 해결책이 존재한다. 대체 r )= ( ) + }서 r r은(는) r 을(를) 나타내며, 이 ID에는 다음과 같은 의미가 부여된다.
여기서 은(는) 통합 상수다. 이 1차 미분 방정식은 분리가 가능하다. 즉, 이(가) 한 쪽에만 나타나도록 다시 배열할 수 있고, 은(는) 다른 쪽에만 나타나도록 다시 배열할 수 있다.[1]
매개변수 는 주어진 광선에 대해 상수지만 렌즈 중심에서 다른 거리에서 통과하는 광선 간에 차이가 있다. 중앙을 통과하는 광선의 경우 0이다. 맥스웰의 어안과 같은 특별한 경우에, 이 첫 번째 순서 방정식은 함수로서 에 대한 공식이나 r{\에 대한 공식을 제공하기 위해 더욱 통합될 수 있다 으로 {{\} 및 r의 상대적인 변화율을 제공한다숫자로 갈아서 렌즈를 통과하는 광선의 경로를 따라갔다.
참고 항목
- BLITS(볼 렌즈 인 더 스페이스) 위성
- 중력렌즈도 방사상으로 굴절률이 감소한다.
참조
- ^ a b Luneburg, R. K. (1944). Mathematical Theory of Optics. Providence, Rhode Island: Brown University. pp. 189–213.
- ^ Brown, J. (1953). Wireless Engineer. 30: 250.
{{cite journal}}: 누락 또는 비어 있음title=(도움말) - ^ Gutman, A. S. (1954). "Modified Luneberg Lens". J. Appl. Phys. 25 (7): 855–859. Bibcode:1954JAP....25..855G. doi:10.1063/1.1721757.
- ^ Morgan, S. P. (1958). "General solution of the Luneburg lens problem". J. Appl. Phys. 29 (9): 1358–1368. Bibcode:1958JAP....29.1358M. doi:10.1063/1.1723441. S2CID 119949981.
- ^ a b "Solutions of problems (prob. 3, vol. VIII. p. 188)". The Cambridge and Dublin Mathematical Journal. Macmillan. 9: 9–11. 1854.
- ^ "Problems (3)". The Cambridge and Dublin Mathematical Journal. Macmillan. 8: 188. 1853.
- ^ Niven, ed. (1890). The Scientific Papers of James Clerk Maxwell. New York: Dover Publications. p. 76.
- ^ "Luneburg lens". www.eahison.com. Retrieved 2021-04-05.
- ^ Lo, Y. T.; Lee, S. W. (1993). Antenna Handbook: Antenna theory. Antenna Handbook. Springer. p. 40. ISBN 9780442015930.
외부 링크
- 유튜브의 루네부르크 렌즈(유전 안테나)를 통한 전파 애니메이션
- 유튜브에서 본 맥스웰의 피시아이 렌즈 애니메이션
- 유튜브의 하프 맥스웰 물고기-아이 렌즈 애니메이션


 1로
1로

 (는) 렌즈의 반지름이다. 표면의 굴절률이 주변 매체의 굴절률과 같기 때문에 표면에서는 반사가 일어나지 않는다. 렌즈 안에서, 광선의 경로는
(는) 렌즈의 반지름이다. 표면의 굴절률이 주변 매체의 굴절률과 같기 때문에 표면에서는 반사가 일어나지 않는다. 렌즈 안에서, 광선의 경로는 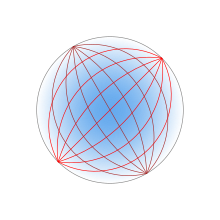







 (는) 진공에서 빛의 속도다. 이
(는) 진공에서 빛의 속도다. 이 
 대한
대한 

 (를) 나타내며,
(를) 나타내며,

 (는)
(는) 


