구면 수차
Spherical aberration| 광학적 수차 |
|---|
 디포커스 |
광학에서 구면 수차(SA)는 구면을 가진 요소를 가진 광학 시스템에서 발견되는 수차의 한 종류입니다.렌즈와 커브드 미러가 대표적인 예입니다.왜냐하면 이 모양은 제조하기 쉽기 때문입니다.구면 중심에서 벗어난 곳에 도달하는 광선은 중심 부근에 도달하는 광선보다 더 적게 굴절되거나 반사된다.이 편차는 광학 시스템에서 생성되는 이미지의 품질을 저하시킵니다.
개요
구면렌즈는 구체의 반지름을 렌즈재의 굴절률로 나눈 반경에만 무계획점(즉 구면수차가 없음)을 가진다.크라운 글라스의 굴절률의 일반적인 값은 1.5(목록 참조)로 구형 렌즈 면적의 약 43%(지름의 67%)만이 유용함을 나타냅니다.그것은 종종 렌즈와 거울의 구형 모양 때문에 초점을 이상적이지 않게 만드는 망원경이나 다른 기구의 불완전성으로 여겨진다.이것은 중요한 효과입니다. 왜냐하면 구형이 비구형보다 훨씬 만들기 쉽기 때문입니다.대부분의 경우 구면 수차를 보상하기 위해 여러 구면 요소를 사용하는 것이 단일 비구면 렌즈를 사용하는 것보다 저렴합니다.
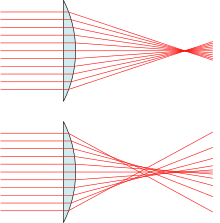
"양성" 구면 수차는 말초 광선이 너무 많이 휘었다는 것을 의미합니다."음" 구면 수차는 말초 광선이 충분히 휘지 않음을 의미합니다.
효과는 직경의 4승에 비례하고 초점 거리의 3승에 반비례하므로 짧은 초점비, 즉 "빠른" 렌즈에서 훨씬 더 두드러집니다.
수정
렌즈 시스템에서는 볼록렌즈와 오목렌즈의 조합 또는 비구면렌즈 또는 무계획렌즈를 사용하여 수차를 최소화할 수 있다.
수차 보정이 있는 렌즈 시스템은 일반적으로 수치 광선 추적을 통해 설계됩니다.단순한 설계의 경우 구면 수차를 최소화하는 매개변수를 분석적으로 계산할 수 있습니다.예를 들어 구면을 가진 단일 렌즈와 소정의 물체 거리 o 화상 거리 i, 굴절률 n으로 이루어진 설계에서는 렌즈 su의 전면과 이면의 및 반지름을 조정함으로써 구면 수차를 최소화할 수 있다.라고 말하다
- } 반지름의 부호는 데카르트 부호 규약을 따른다
초점비가 f/10보다 짧은 구형 거울을 사용하는 소형 망원경의 경우, 먼 점 소스(별 등)의 빛이 모두 같은 점에 집중되지 않는다.특히 거울의 내부를 때리는 빛은 외부를 때리는 빛보다 거울에서 더 멀리 초점을 맞춘다.그 결과, 수차가 존재하지 않는 것처럼 화상의 초점을 선명하게 맞출 수 없다.구면 수차로 인해 초점비가 f/10 미만인 망원경은 일반적으로 비구면 거울 또는 보정 렌즈를 사용하여 제작된다.
비구면 렌즈를 만드는 것으로, 구면 수차를 없앨 수 있다.데카르트는 표면이 잘 선택되는 데카르트 난형(중심 대칭 축을 중심으로 회전)인 렌즈가 축의 한 지점 또는 축 방향으로 무한대의 빛을 완벽하게 촬영할 수 있다는 것을 보여주었다.이러한 설계에 의해, 원거리 [1]광원으로부터의 빛의 초점이 완전히 어긋나지 않게 됩니다.
2018년에는 라파엘 G. 곤살레스-아쿠냐와 엑토르 A.멕시코 국립 자치 대학과 멕시코의 몬테레이 공과 고등 교육 연구소의 대학원생인 차파로 로모는 구면 [2][3][4]수차를 제거하는 렌즈 표면의 닫힌 공식을 발견했다.이 방정식은 렌즈의 한 면에 대한 모양을 지정하기 위해 적용될 수 있으며, 다른 표면은 주어진 모양을 가지고 있습니다.
이상 스폿 직경의 추정
구면 수차로 인해 초점을 맞춘 지점의 직경을 추정하는 많은 방법은 광선 광학에 기초한다.그러나 광선광학에서는 빛이 전자파라고 생각하지 않는다.따라서 간섭 효과로 인해 결과가 잘못될 수 있습니다.
코딩턴 표기법
광선 광학에 기초한 비교적 단순한 형식주의는 얇은 렌즈에만 적용되는 코드딩턴 [5]표기법이다.다음 중 n은 렌즈의 굴절률, o는 피사체 거리, i는 화상 거리, h는 최외선이 렌즈에 입사하는 으로부터의 거리 ({은 제1렌즈 반경, 스타일 는 제2렌즈 반경, f는 렌즈 초점 거리이다.거리 h는 투명 개구부의 절반으로 이해할 수 있습니다.
형상, s 및 위치에 대한 코딩턴 요인을 사용하여 p,
![{\displaystyle {\begin{aligned}s&={\frac {R_{2}+R_{1}}{R_{2}-R_{1}}}\\[8pt]p&={\frac {i-o}{i+o}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/153e0891f9c02c41916455af75e53445456ccee3)
세로 구면 수차를 다음과 같이 쓸 수 있다
초점 거리 f가 세로 구면 수차 LSA보다 매우 크면 초점 직경에 해당하는 가로 구면 수차 TSA는 다음과 같이 주어진다.
「 」를 참조해 주세요.
레퍼런스
- ^ Villarino, Mark B (2007). "Descartes' perfect lens". arXiv:0704.1059 [math.GM].
- ^ Machuca, Eduardo (July 5, 2019). "Goodbye Aberration: Physicist Solves 2,000-Year-Old Optical Problem". PetaPixel. Retrieved July 10, 2019.
- ^ González-Acuña, Rafael G.; Chaparro-Romo, Héctor A. (2018). "General formula for bi-aspheric singlet lens design free of spherical aberration". Applied Optics. 57 (31): 9341–9345. arXiv:1811.03792. Bibcode:2018ApOpt..57.9341G. doi:10.1364/AO.57.009341. PMID 30461981. S2CID 53695913.
- ^ Liszewski, Andrew (August 7, 2019). "A Mexican Physicist Solved a 2,000-Year Old Problem That Will Lead to Cheaper, Sharper Lenses". Gizmodo. Retrieved August 7, 2019.
- ^ a b Smith, T. T. (1922). "Spherical Aberration in thin lenses". Scientific Papers of the Bureau of Standards. 18: 559–584. doi:10.6028/nbsscipaper.127.
