조석 잠금

한 쌍의 공궤도 천체들 사이의 조석 잠금은 천체들 중 하나가 완전한 궤도를 도는 동안 더 이상 그것의 회전 속도에 변화가 없는 상태에 도달했을 때 발생합니다.조밀하게 잠긴 물체가 동기 회전을 하는 경우, 물체는 자신의 축을 중심으로 회전하는 데 파트너 주위를 회전하는 데 걸리는 시간만큼 시간이 걸립니다.예를 들어, 달의 궤도가 완전히 원형인 것은 아니기 때문에 약간의 변화가 있기는 하지만 달의 같은 면이 항상 지구를 향한다.보통 위성만 큰 본체에 ^[1]고정된다.그러나 두 물체 사이의 질량 차이와 거리가 비교적 작다면, 명왕성과 카론의 경우처럼 서로 조밀하게 고정될 수 있다.조석 잠금 프로세스의 다른 이름은 중력 잠금,^[2] 포착 회전 및 스핀-궤도 잠금입니다.

그 효과는 두 물체의 중력의 상호작용이 물체의 회전을 느리게 할 때 그것이 완전히 고정될 때까지 발생한다.수백만 년에 걸쳐, 상호작용은 에너지 교환과 열 방산의 결과로 그들의 궤도와 회전 속도를 변화시킵니다.천체 중 하나가 완전한 궤도에 걸쳐 회전 속도가 더 이상 순변화하지 않는 상태에 도달하면, 그것은 조석적으로 ^[3]잠긴다고 한다.물체를 방치하면 시스템에 에너지를 다시 공급해야 하기 때문에 물체는 이 상태를 유지하는 경향이 있습니다.예를 들어 거대한 행성이 물체를 교란할 경우, 물체의 궤도는 조석 잠금을 해제하기 위해 시간이 지남에 따라 이동할 수 있습니다.

조수 잠금이 동기 ^[4]회전을 수반하는 것은 아닙니다.예를 들어, 수성에서는, 이 조석으로 잠긴 행성은 태양 주위를 두 바퀴 돌 때마다 3회 회전을 완료하며, 이는 3:2 회전-궤도 공명입니다.달과 같이 궤도가 거의 원형에 가깝고 물체의 회전축이 크게 기울지 않은 특별한 경우, 조석정지에 의해 회전하는 물체의 같은 반구가 항상 ^[3][4][5]상대방을 향하게 됩니다.그러나 이 경우 신체의 정확히 동일한 부분이 항상 모든 궤도에서 파트너를 향하지는 않습니다.잠긴 물체의 궤도 속도 및 회전축 기울기의 변화로 인해 약간의 이동이 있을 수 있습니다.

메커니즘

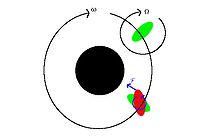
A와 B라는 한 쌍의 공궤도를 도는 물체를 생각해 봅시다.차체 B를 보다 큰 차체 A에 조밀하게 고정하기 위해 필요한 회전률의 변화는 조력에 의해 B에 유도된 돌출부에 A의 중력에 의해 ^[6]가해지는 토크로 인해 발생한다.

물체 A에서 B로 향하는 중력은 거리에 따라 달라지며, 가장 가까운 표면에서, 그리고 가장 먼 표면에서 가장 커집니다.이것은 물체 B를 가로지르는 중력 구배를 만들어 B의 평형 모양을 약간 왜곡시킵니다.물체 B의 본체는 A를 향하는 축을 따라 길어지고 반대로 이 축과 직교하는 방향으로 치수가 약간 감소한다.이 길쭉한 일그러짐은 조석 융기라고 알려져 있다. (고체 지구의 경우, 이러한 융기는 약 0.4m 또는 1피트 4인치까지 변위할 수 있다.)^[7]B가 아직 제대로 잠기지 않았을 때, 두 개의 "높은" 조석 융기 중 하나가 물체 A가 머리 위에 있는 지점 가까이 이동하면서 궤도 운동으로 인해 B의 표면 위를 이동합니다.자기 중력으로 인해 거의 구형에 가까운 큰 천체의 경우, 조석 왜곡은 약간 프로레이트 구상체, 즉 장축을 따라 연장된 축대칭 타원체를 생성한다.작은 물체에서도 왜곡이 발생하지만, 이 왜곡은 덜 규칙적입니다.

B의 재료는 조력에 의해 발생하는 이러한 주기적인 형상에 저항력을 발휘한다.사실상, B를 중력 평형 형상으로 다시 형성하기 위해서는 어느 정도의 시간이 필요하며, 이때 형성되는 팽대부는 B의 회전에 의해 이미 A-B 축으로부터 어느 정도 떨어진 곳으로 이동되었다.공간의 유리한 지점에서 볼 때, 최대 팽대부 연장점은 A 방향으로 향하는 축에서 변위한다.B의 회전주기가 공전주기보다 짧으면 팽대부는 A를 향해 회전방향으로 축을 향해 전진하는 반면 B의 회전주기가 길면 팽대부는 뒤처진다.

팽대부가 이제 A-B 축에서 변위하기 때문에, 팽대부의 질량에 대한 A의 중력은 B에 토크를 가합니다.A를 향한 돌출부의 토크는 B의 공전 주기에 맞춰 B의 회전을 가져오는 반면, A를 향한 "뒤쪽" 돌출부는 반대 의미로 작용합니다.그러나 A를 향한 쪽의 벌지는 B의 직경만큼 후방 벌지보다 A에 가깝기 때문에 약간 더 강한 중력과 토크가 발생한다.따라서 양쪽 돌출에서 발생하는 순 토크는 항상 B의 회전을 궤도 주기와 동기화시키는 방향으로 작용하며, 결국 조석 잠김으로 이어집니다.

궤도 변화

이 과정에서 전체 A-B 시스템의 각운동량은 보존되므로 B가 회전각운동량을 잃으면 B의 궤도각운동량은 비슷한 양만큼 상승한다(A의 회전에도 약간의 영향이 있다).이로 인해 B의 회전 속도가 느려짐에 따라 A에 대한 B의 궤도가 상승합니다.B가 너무 느리게 회전하기 시작하는 다른 경우, 조석 잠금은 B의 회전 속도를 높이고 궤도를 낮춥니다.

대형 바디의 잠금

조석 고정 효과는 큰 물체 A에서도 나타나지만 B의 질량이 작기 때문에 B의 중력 효과가 약하기 때문에 느린 속도로 나타난다.예를 들어, 지구의 자전은 달에 의해 서서히 느려지고 있는데, 화석 ^[8]기록에서 알 수 있듯이 지질학적 시간이 지나면서 눈에 띄게 된다.현재 추정치는 이것이 (태양의 조석 영향과 함께) 지구의 날을 약 6시간에서 현재 24시간으로 연장하는데 도움이 되었다고 한다(40억 년 이상).현재 원자시계는 ^[9]지구의 하루가 세기당 평균 약 2.3밀리초씩 연장된다는 것을 보여준다.충분한 시간이 주어진다면, 이것은 지구와 달 사이에 상호 조수 차단을 만들어 낼 것이다.지구의 낮의 길이가 늘어나고 음력 달의 길이도 늘어날 것이다.지구의 항성일은 결국 달의 공전 주기와 같은 길이를 갖게 되는데, 이는 현재 지구의 하루 길이의 약 47배이다.그러나 태양이 적색 거성이 되어 지구와 ^[10][11]달을 흡수하기 전에는 지구가 달에 조석적으로 고정되지 않을 것으로 예상된다.

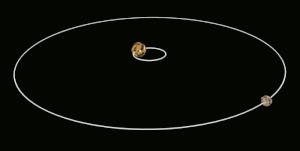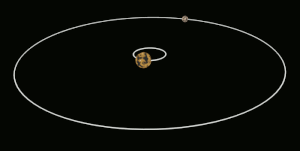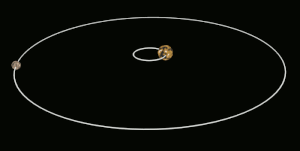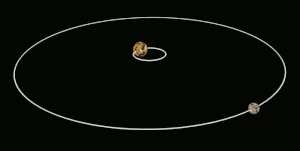
유사한 크기의 물체의 경우, 효과는 양쪽 모두에 대해 비슷한 크기일 수 있으며, 두 물체는 훨씬 짧은 시간 내에 서로 조밀하게 잠길 수 있다.한 예로 왜소행성 명왕성과 위성 카론이 있다.그들은 이미 명왕성의 한 반구에서만 카론이 보이는 상태에 도달했고 그 반대도 ^[12]마찬가지이다.

편심 궤도

널리 퍼진 오해는 잘 잠긴 몸이 영구적으로 한쪽을 숙주로 돌린다는 것이다.

--

이심률이 0에 가깝지 않은 궤도의 경우, 두 물체 사이의 가장 강한 조석 상호작용 지점인 근점에 있을 때 회전 속도는 궤도 속도에 따라 고정되는 경향이 있다.궤도를 도는 물체에 동반자가 있는 경우, 이 제3의 물체는 부모 물체의 회전 속도를 진동하는 방식으로 변화시킬 수 있다.이러한 상호작용은 또한 1차 주위에서 궤도를 도는 물체의 궤도 이심률 증가를 유도할 수 있으며, 이는 편심 ^[13]펌핑이라고 알려져 있다.

궤도가 편심하고 조석 효과가 상대적으로 약한 경우에, 작은 물체는 조석적으로 고정되는 것이 아니라 소위 스핀-오빗 공명 상태에 빠질 수 있습니다.여기서 물체의 공전 주기와 자기 궤도 주기의 비율은 1:1과는 다소 다른 간단한 분수를 나타낸다.잘 알려진 사례는 수성의 자전으로, 수성은 3:2의 ^[2]공명으로 태양 주위를 공전하고 있다.이로 인해 회전 속도는 ^[14]근일점 주위의 궤도 속도와 대략 일치합니다.

많은 외계 행성들(특히 가까이 있는 행성들)은 1:1 이상의 스핀-궤도 공명 상태에 있을 것으로 예상된다.예를 들어, 수성과 비슷한 지구형 행성은 3:2, 2:1 또는 5:2 스핀-오빗 공명으로 포착될 수 있으며, 각 행성은 궤도 ^[15]이심률에 따라 달라질 수 있습니다.

발생.

달

태양계의 19개의 알려진 위성은 모두 원형으로 되어 있는데, 그 이유는 그것들이 매우 가까이 궤도를 돌고 있고 ^[16]거리가 줄어들면서 조력이 빠르게 증가하기 때문입니다.반면에, 잘 알려진 큰 위성들보다 훨씬 더 멀리 궤도를 도는 가스 거대 위성들(예: 피비)의 불규칙한 외부 위성들은 조석적으로 잠겨있지 않다.

명왕성과 카론은 조류 자물쇠의 극단적인 예이다.카론은 주성에 비해 상대적으로 큰 달이며 또한 매우 가까운 궤도를 가지고 있다.그 결과 명왕성과 카론은 서로 조밀하게 잠기게 됩니다.명왕성의 다른 위성들은 조석으로 고정되어 있지 않다; 스틱스, 닉스, 케르베로스, 그리고 히드라는 모두 ^[17]카론의 영향으로 무질서하게 회전한다.

소행성 위성들의 조석 잠김 상황은 거의 알려지지 않았지만, 근접 궤도를 도는 쌍성들은 ^{[citation needed]}조석 잠김과 동시에 접촉 쌍성들이 잠길 것으로 예상된다.

지구의 달

지구의 달의 자전과 공전 주기는 서로 조밀하게 고정되어 있기 때문에 지구에서 달이 언제 관측되든 달의 같은 반구가 항상 보입니다.달의 뒷면은 1959년 소련의 우주선 루나 ^[18]3호에서 대부분의 뒷면 사진이 전송될 때까지 보이지 않았다.

달에서 지구를 관찰할 때, 지구는 하늘을 가로질러 움직이는 것처럼 보이지 않는다.그것은 ^[19]축을 중심으로 회전할 때 거의 모든 표면을 보여주면서 같은 위치에 있다.

달의 자전과 공전 주기가 정확히 고정되어 있음에도 불구하고, 자전과 시차 현상으로 인해 달 전체 표면의 약 59%가 지구에서 반복적으로 관찰될 수 있다.위성은 주로 궤도의 이심률로 인해 달의 궤도 속도가 변화하기 때문에 발생한다: 이것은 달의 주위를 따라 약 6° 더 볼 수 있게 해준다.시차는 기하학적 효과이다: 지구 표면에서 관측자는 지구와 달의 중심을 통과하는 선에서 오프셋되며, 이로 인해 달이 국지적 ^[20]지평선에 있을 때 달의 측면 주위에 약 1° 더 많은 것을 볼 수 있다.

행성

한동안 수성이 태양과 동시에 자전하는 것으로 생각되었다.이것은 수성이 관측하기에 가장 좋은 위치에 있을 때마다 같은 면이 안쪽으로 향했기 때문입니다.1965년 레이더 관측 결과 수성은 태양 주위를 두 바퀴 돌 때마다 3번 회전하는 3:2 스핀-궤도 공명을 일으켜 관측 지점에서 같은 위치에 있는 것으로 나타났다.모델링은 수성이 형성되고 나서 아마도 1000만 ^[21]년에서 2000만 년 이내에 역사상 매우 초기에 3:2 스핀-오빗 상태로 포착되었음을 증명했습니다.

금성과 지구 사이의 연속적인 근접 접근 사이의 583.92일의 간격은 5.001444 금성 태양일과 같으며, 근접 접근 시 지구에서 거의 같은 얼굴을 볼 수 있게 한다.이 관계가 우연히 생겨난 것인지 아니면 지구와의 어떤 조수 고정의 결과인지는 알려지지 않았다.^[22]

2016년 프록시마 센타우루스자리 주위를 도는 외계 행성 프록시마 b는 ^[23]수성과 같은 회전이나 3:2 회전 궤도 공명을 나타내며 조석적으로 잠겨 있다.

조석으로 고정된 가상의 외계행성의 한 가지 형태는 안구 행성이고, 안구 행성은 다시 "뜨거운" 안구 행성과 "차가운" 안구 ^[24][25]행성으로 나뉩니다.

별들

우주의 가까운 쌍성은 서로 조석적으로 잠겨 있을 것으로 예상되며, 주성 주위를 매우 가깝게 도는 것으로 밝혀진 외계 행성들 또한 조석적으로 잠겨 있는 것으로 생각됩니다.MOST에 의해 확인된 특이한 예로는 목동자리 타우가 있을 수 있는데, 목동자리 타우 ^[26]b는 목동자리 행성 타우 b에 의해 조석적으로 잠겨 있을 것이다.만약 그렇다면, 조수 차단은 거의 확실히 ^[27][28]상호적이다.

타임스케일

다음 ^[29]공식을 사용하여 물체가 완전히 잠길 때까지의 시간을 추정할 수 있습니다.

$(*displaystyle t_{\text{lock}}) 약(*frac**a^{6})IQ}{3Gm_{p}^{2}k_{2}R^{5}}}}$

어디에

• $§(\displaystyle$ \obega$,$ )는 초당 라디안 단위로 표시되는 초기 회전 속도입니다.
• $\$ a$,\$는 행성 주위의 위성 움직임의 반장축이다(근점 및 근점 거리의 평균으로 표시됨).
• $({$ $I$$}$${\displaystyle 0}$0.${\displaystyle {}_{}{}^{}}$ s $({$\ 약$0$.4$\;m_{s}R^{2}})$는 위성의 관성모멘트입니다.${\displaystyle {여기}_{}}$서$$m({$displaystyle m_{s})$은 위성의 질량, $(\displaystyle$ R$)$은 위성의 평균 반지름입니다.
• $($ Q$)$는 위성의 소산 함수입니다.
• $G($디스플레이 스타일 G$)$는 중력 상수입니다.
• ${\displaystyle m_{}{}_{}}$p { $display style$ m _ { $p$} is$$ 、 행성의 질량(즉, 궤도를 도는 물체)입니다.
• ${\displaystyle {k\mathrm{}}_{}}$ 2$displaystyle k_{2})$는 위성의 조석 사랑 번호입니다.

$(\displaystyle$ Q$)$ $및$ $(\$ $k_$${2})$는 ${\displaystyle {k2\mathrm{}}_{}}$/ ${\displaystyle Q}$ ${\displaystyle =0}$.$0011인$ 달을 제외하고는 일반적으로 매우 잘 알려져 있지 않습니다. Q(\$displaystyle Q_$${2}/Q= 0.0011$는 일반적으로 약 $100($잠금 시간 초과 추정, 약 100$)$에 $해당$합니다.,그리고.

${\displaystyle k_{2}\약 {1+{\frac {19\mu}{2\rho gR}}}}},$

어디에

• $§$ $(\displaystyle$ \rho $)$는 위성의 ${\displaystyle \mathrm{밀도}}$입니다.
• ${\displaystyle g}$ ${\displaystyle †}$ ${\displaystyle {Gm}_{}}$s / ${\displaystyle R{}^{}}$ (\$displaystyle$ g$\approx$ Gm_${s}/R^{2})$는 위성의 표면 중력입니다.
• ${\displaystyle }$μ$(\$ )는$$ 위성의 ${\displaystyle \mathrm{강성}}$입니다.이는 대략 암석 물체의 경우 3×10¹⁰ N·m⁻², 얼음 물체의 경우 4×10⁹ N·m로⁻² 볼 수 있다.

인공위성의 크기와 밀도를 알고 있어도 추정해야 할 파라미터(특히 θ, Q 및 μ)가 많이 남으므로 계산된 잠금시간은 10계수까지 부정확할 것으로 예상된다.또한 조석 잠금 단계에서는 이후의 조석 가속으로 인해 $a$가 현재 관측된 것과 크게 다를 수 있으며, 잠금 시간은 이 값에 매우 민감합니다.

불확실성이 매우 높기 때문에 위의 공식은 다소 덜 번거로운 공식을 제공하기 위해 단순화할 수 있다.위성이 $구형$이라고 가정하면 k ${\displaystyle \mathrm{2\mu 1}{}_{}}$Q ${\displaystyle =}$ $({displaystyle k_{2}\ll$ 1,$Q=100$ 초기 잠기지 않은 상태에서 12시간마다 1바퀴 도는 것이 현명하다(대부분의 소행성은 약 2시간에서 약 2일 사이의 회전 주기를 가진다).

${\displaystyle t_{\text{lock}\약 6\{frac {a^{6}R\mu}{m_{p}^{2}}\times 10^{10}\{text{years}}},$^[30]

질량(kg), 거리(m) $및{\displaystyle }$μ(\$displaystyle\mu)$를 m2당 뉴턴 단위로 $나타내며{\displaystyle }$,$$μ(\$displaystyle\mu)$는 암석 물체의 경우 대략 3×10N¹⁰·m, 얼음 물체의 경우 4⁹×10N⁻²·m로⁻² 볼 수 있습니다.

$a$에 대한 의존도가 매우 높다$.$

명왕성의 경우처럼 주체를 위성에 고정하기 위해 위성과 주체의 파라미터를 교환할 수 있습니다.

한 가지 결론은 다른 조건($예$를 $들어$$Q와 μ$등)이 같다면 큰 달은 행성에서 같은 궤도 거리에 있는 작은 달보다 더 빨리 잠기게 된다는 것입니다. 왜냐하면 $displaystyle m_{s})$은 위성 $반지름{\displaystyle }$ R$(\displaystyle$ R$)$의 큐브에 따라 커지기 $때문$입니다.예를 들어, 토성계에서는 히페리온이 조석적으로 잠겨 있지 않지만, 보다 먼 거리를 도는 큰 이아페투스는 잠겨 있습니다.하지만, 히페리온은 타이탄 근처에서도 강한 추진력을 경험하기 때문에 그것의 회전이 혼란스러울 수밖에 없기 때문에, 이것은 명확하지 않다.

잠금 시간 ${\displaystyle 척도}$에 대한 위의 공식은 ${\displaystyle {k\mathrm{}}_{}}$2 /$$Q(\displaystyle $k_{2}/Q$의 주파수 의존성을 무시하기 때문에 크기순으로 다를 수 있다. 더 중요한 것은 이러한 물체의 스핀-오빗 역학은 정의되어 있기 때문에 점성 쌍성(이중 별 또는 이중 소행성)에는 적용되지 않을 수 있다.d 주로 ^[31]강성이 아닌 점도에 의해 결정된다.

잘 잠긴 시신 목록

태양계

모체	조석 위성[32]
태양.	수성[33][34][21](3:2 스핀-오빗 공명)
지구	달
화성	포보스[35]·데이모스[36]
목성	메티스[37]·아드라스테아·아말테아[37]·테베[37]·이오·유로파·가니메데·칼리스토
토성	판도라스·프로메테우스·판도라·에피메테우스·야누스·미마스·엔셀라두스[38]·텔레스토·테티스[38]·칼립소·디오네[38][38]·레아·타이탄·이아페투스[38]
천왕성	미란다 · 아리엘 · 움브리엘 · 티타니아 · 오베론
해왕성	프로테우스·트리톤[35]
명왕성	Charon (Pluto 자체는 Charon에 [12]잠겨 있습니다)

태양계 외

• 가장 성공적인 외계행성의 발견 방법(통과 속도 및 방사 속도)은 항성 근처의 행성 탐지에 유리한 명확한 관측 편중으로 인해 어려움을 겪고 있으며, 따라서 발견된 외계행성의 85%가 조석 고정 구역 안에 있기 때문에 ^[39]이 현상의 실제 발생률을 추정하기가 어렵다.목동자리 타우는 근접 궤도를 도는 거대 행성 목동자리 타우 ^[26]b에 갇혀 있는 것으로 알려져 있다.

잠길 것 같은 시체

태양계

물체를 주 궤도에 가두는 데 필요한 시간과 현재 궤도에 있는 시간(대부분의 행성 위성의 태양계 나이와 비교 가능) 사이의 비교에 기초하여, 많은 위성이 잠겨 있는 것으로 생각됩니다.그러나 이러한 회전은 알려져 있지 않거나 충분히 알려져 있지 않습니다.다음과 같습니다.

아마도 토성에 갇혀 있을 것이다.

아마 천왕성에 잠겨 있을 것이다.

아마도 해왕성에 잠겼을 것이다.

엑스트라솔라

• 글리제 581c,^[40] 글리제 581g,^[41][42] 글리제 581b,^[43] 글리제 581e는^[44] 모항성 글리제 581에 조석적으로 잠겨 있을 수 있습니다.글리제 581d는 거의 ^[45]확실히 같은 별과의 2:1 또는 3:2 스핀-궤도 공명으로 포착된다.
• TRAPPIST-1 계의 모든 행성은 조석적으로 ^[46][47]잠겨 있을 것이다.

「 」를 참조해 주세요.

• 각운동량 보존
• 어스 밀물 #효과
• 중력 경사 안정화 – 다양한 우주선의 안정화 및 방향 설정 방법
• 코자이 메커니즘 – 멀리 있는 제3의 물체에 의해 교란되는 바이너리 시스템의 궤도에 영향을 미치는 동적 현상
• 궤도 공명 – 두 궤도를 도는 천체가 서로에게 가해지는 규칙적이고 주기적인 중력 영향
• 행성 거주 가능성 – 행성이 생명체에 적합한 것으로 알려진 범위
• Roche 한계 – 위성을 분해하는 궤도 반지름
• 동기 궤도
• 조석가속 – 조석잠금이 발생하는 자연현상

레퍼런스