회전 분광법

회전분광법은 기체상의 분자의 양자화된 회전상태 사이의 전이 에너지 측정과 관련이 있다.극성 분자의 스펙트럼은 마이크로파^[1] 분광법 또는 원적외선 분광법으로 흡수 또는 방출을 측정할 수 있다.비극성 분자의 회전 스펙트럼은 이러한 방법으로는 관측할 수 없지만, 라만 분광법으로 관측하고 측정할 수 있다.회전분광학(Rotational Spectroopy)은 진동에너지의 변화와 함께 회전에너지의 변화가 일어나는 회전-진동분광학(Ro-vibronic spectroopy) 및 회전, 진동 및 전자 에너지가 함께 발생하는 회전-진동분광학(또는 단순히 진동-전자분광학)과 구별하기 위해 순수 회전분광학(pectrocopy)이라고 부르기도 한다.변경이 동시에 발생합니다.

회전 분광학의 경우, 분자는 대칭에 따라 구면 상판, 선형 상판 및 대칭 상판으로 분류됩니다. 분석식은 이러한 분자의 회전 에너지 항에 대해 도출될 수 있습니다.J=3까지의 회전 수준에 대해 네 번째 범주인 비대칭 상판에 대한 분석식을 도출할 수 있지만, 더 높은 에너지 수준은 수치 방법을 사용하여 결정해야 한다.회전 에너지는 이론적으로 분자를 강체로 간주하고 원심 왜곡, 미세 구조, 초미세 구조 및 코리올리 결합을 설명하기 위해 추가 용어를 적용하여 도출됩니다.이론적 표현에 스펙트럼을 적합시키면 유리한 경우 분자 결합 길이와 각도의 매우 정밀한 값이 도출될 수 있는 관성 모멘트의 수치 값을 얻을 수 있다.정전장이 존재하는 경우 분자 전기 쌍극자 모멘트를 결정할 수 있는 스타크 분할이 있습니다.

회전 분광학의 중요한 응용 분야는 전파 망원경을 이용한 성간 매체의 화학적 조성을 탐구하는 것이다.

적용들

회전 분광학은 주로 분자 물리학의 근본적인 측면을 조사하는데 사용되어 왔다.그것은 기상 분자의 분자 구조를 결정하기 위한 독특한 정밀한 도구입니다.클로로톨루엔(CHCl
_7
7)^[2]의 CHCl기에
_6
4 대한 CH 그룹의
₃ 회전과 관련된 내부 회전 장벽을 확립하는 데 사용할 수 있다.미세 또는 초미세 구조를 관찰할 수 있을 때, 이 기술은 분자의 전자 구조에 대한 정보도 제공합니다.현재 판데르발스, 수소, 할로겐 결합과 같은 약한 분자 상호작용의 본질에 대한 많은 이해는 회전 분광학을 통해 확립되었다.전파 천문학과 관련하여, 이 기술은 성간 매체의 화학적 조성을 탐구하는 데 중요한 역할을 한다.마이크로파 천이는 실험실에서 측정되며 전파 망원경을 사용하여 성간 매체의 방출과 일치합니다.NH는
₃ 성간 ^[3]매질에서 확인된 최초의 안정적인 다원자 분자였다.일산화염소의^[4] 측정은 대기 화학에서 중요하다.현재 우주화학 프로젝트는 실험실 마이크로파 스펙트럼 분석과 Atacama Large Millimeter/submillimeter Array(ALMA)^[5]와 같은 최신 방사선 망원경을 사용한 관측을 모두 포함한다.

개요

기체상의 분자는 분자의 질량 중심을 중심으로 공간 내에서 고정된 방향의 상호 직교축 세트에 대해 자유자재로 회전한다.분자간 힘의 존재로 인해 액체상 또는 고체상 분자의 경우 자유 회전이 불가능합니다.각 고유 축에 대한 회전은 해당 축에 대한 관성 모멘트와 양자 수에 의존하는 양자화된 에너지 레벨의 세트와 관련된다.따라서 선형 분자의 경우 에너지 수준은 단일 관성 모멘트와 단일 양자수 $J{\displaystyle }$($회전$ 각운동량의 크기를 정의하는 J$\displaystyle$ J$)$로 설명됩니다.

대칭 로터(또는 대칭 상단 - 다음 섹션 참조)인 비선형 분자의 경우, 관성 모멘트가 2개 있으며, 에너지는 또한 주 대칭 ^[6]축을 따라 회전 각운동량의 벡터 성분을 정의하는 두 번째 회전 양자수 $(\displaystyle$K)에 의존합니다.아래 식과 함께 스펙트럼 분석 데이터를 분석하면 관성 모멘트의 값을 정량적으로 결정할 수 있다.이러한 분자 구조 및 치수의 정확한 값으로부터 얻을 수 있다.

선형분자에 대해 회전스펙트럼의 분석은 분자의 회전상수^{[notes 2]} 및 관성모멘트의 값을 제공하며 원자질량을 알면 결합길이를 직접 결정하는데 사용할 수 있다.이원자 분자의 경우 이 과정은 간단하다.두 개 이상의 원자를 가진 선형 분자의 경우 OCS¹²³² 및¹²³⁴ OCS와 같은 두 개 이상의 등방성 물질의 스펙트럼을 측정할 필요가 있다.이를 통해 결합 ^{[notes 3]}길이에 대해 일련의 연립 방정식을 설정하고 해결할 수 있습니다.이렇게 해서 얻을 수 있는 결합길이는 평형결합길이와 약간 다르다.이는 회전 상태가 참조하는 진동 지면 상태에는 제로점 에너지가 존재하지만, 평형 결합 길이는 잠재 에너지 곡선에서 최소값이기 때문이다.회전 상수 간의 관계는 다음과 같습니다.

$\displaystyle B_{v}=B-\alpha \left(v+{\frac {1}{2}}\right)}$

여기서 v는 진동 양자수이고 α는 진동-회전 상호작용 상수이며, 두 개의 다른 진동 상태에 대한 B 값이 발견될 ^[7]경우 계산될 수 있습니다.

다른 분자의 경우 스펙트럼이 분해되고 결합 길이와 결합 각도에 할당된 개별 전이를 추론할 수 있다.대부분의 비대칭 상단과 같이 이것이 불가능할 때, 할 수 있는 모든 것은 가정된 분자 구조에서 계산한 세 가지 관성 모멘트에 스펙트럼을 맞추는 것이다.분자구조를 변화시킴으로써 적합도를 향상시켜 구조의 정성적 추정치를 얻을 수 있다.동위원소 치환은 분자 구조의 결정에 이 접근방식을 사용할 때 매우 중요하다.

분자 로터의 분류

양자역학에서는 분자의 자유 회전이 양자화되므로 회전 에너지와 각운동량은 단순히 분자의 관성 모멘트($\displaystyle$ I$)$와 관련된 일정한 값만 취할 수 있습니다.모든 분자에 대해 세 가지 관성 모멘트가 있습니다.${\displaystyle I_{}}$ A$(\$ I_${A$ ${\displaystyle I_{}}$ B$(\$ I_${B$$})$ 및$$ C(\$displaystyle I_{C})$는 시스템의 질량 중심을 원점으로 하여 서로 직교하는 3개의 축 A, B, C(\displaystyle I_{C}.이 문서에서 사용되는 일반 규칙은 I ${\displaystyle A_{}}$ $\$$displaystyle$$I_{A}\leq$ I_${B}\leq I_{C$와 같이$$ 최소 관성 모멘트에 대응하는 축을 정의하는 것입니다$.$그러나 일부 저자는$$A축($style A축$)을 최고 순서의 분자 회전축(molecular rotation axism)으로$$ 정의한다.

분자에 대한 에너지 수준의 특정 패턴(따라서 회전 스펙트럼의 전환)은 그 대칭에 의해 결정된다.분자를 보기 위한 편리한 방법은 분자를 구조의 대칭에 따라 4개의 다른 클래스로 나누는 것입니다.이것들은

Spherical tops (spherical rotors)

세 가지 관성 모멘트는 모두 서로 동일합니다.$displaystyle$$I_{B}=I_{C$ 구형 팽이의 예로는 사염화인(P
₄), 사염화탄소(CCL
₄) 및 기타 사할라이드, 메탄
₄(CH), 실란(SiH
₄), 육불화황(SF)
₆ 및 기타 헥사플루오르화물이 있다.모든 분자는 입방체 점군_d T 또는_h O에 속합니다.

Linear molecules

선형 분자의 경우 관성 모멘트는 ${\displaystyle I_{}}$ A${\displaystyle {}_{}{i}_{}}$ I ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ I ${\displaystyle C_{}}${ $display style$I_{$A}\ll I_${B} $=$에 $의해{\displaystyle {}_{}}$ 관련된다.$I_{C$ 대부분의 경우 ${$ I_${A}}$는 0으로 간주할 수 있습니다.선상분자의 예로는 디옥시겐
₂, O, 디니트로겐
₂, N, 일산화탄소, CO, 히드록시기, OH, 이산화탄소₂, CO, 시안화수소, HCN, 황화카르보닐, OCS, 아세틸렌(에틴, HCchCH) 및 디할로에틸렌이 있다.이 분자들은 점군_∞v C 또는_∞h D에 속합니다.

Symmetric tops (symmetric rotors)

대칭 상판은 두 ${\displaystyle {관성}_{}}$ ${\displaystyle {모멘트}_{}}$가 $동일$한 분자, I A$=$ I B { style I_{A} ${\displaystyle {}_{}}$$I_{B}}$ $또는$ ${\displaystyle {IB}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle I_{}}$ C$${ $displaystyle I_{B$} $=$$I_{C$ 정의상 대칭 상판은 3배 이상의 회전 축을 가져야 합니다.편의상 분광학자는 분자를 < I \ $display I_{$A} $=$ Oblate symmetric tops (접시 또는 디스크 모양)의 두 등급으로 나눈다.$I_{B}<I_{C}}$ 및 프롤레이트 대칭 탑(축구 또는 시가 모양) ( A< C{ $displaystyle$ I_${A}$ <)$I_{B}=I_{C$ 스펙트럼은 다소 다르게 보이며 즉시 인식할 수 있다.대칭 상의의 예는 다음과 같습니다.

삭제하다

벤젠, CH
_6
6, 암모니아, NH
₃, 사불화 제논, XeF
₄

프롤레이트

클로로메탄, CHCl
₃, 프로핀, CHCchCH
₃

상세한 예로서 암모니아는 3중 회전 축에 대한 관성_C 모멘트 I = 4.4128 × 10⁻⁴⁷ kg² m, C 축에₃ 수직인 축에 대한 모멘트_A I = 2_B.8059 × 10⁻⁴⁷ kg² m를 가진다.독특한 관성 모멘트가 다른 두 개보다 크기 때문에 분자는 타원형의 ^[8]대칭 꼭대기이다.

Asymmetric tops (asymmetric rotors)

세 관성 모멘트의 값은 서로 다릅니다.비대칭 꼭대기인 작은 분자의 예로는 물, HO
₂, 이산화질소가 있으며
₂, NO의 대칭축은 2배 회전축이다.대부분의 큰 분자는 비대칭 윗부분이다.

선택 규칙

마이크로파 및 원적외선 스펙트럼

회전 상태 간의 전이는 영구적인 전기 쌍극자 ^{[9][notes 4]}모멘트를 가진 분자에서 관찰될 수 있다.이 규칙의 결과로 극성이 아닌 N(이질소) 또는 HCCH(에틴)와 같은
₂ 중심대칭 선형 분자에 대해 마이크로파 스펙트럼을 관찰할 수 없다.제로 쌍극자 모멘트와 등방성 분극성을 모두 갖는 CH(메탄)와
₄ 같은 사면체 분자는 원심 왜곡의 효과를 제외하고 순수한 회전 스펙트럼을 가지지 않는다. 분자가 3배 대칭 축을 중심으로 회전할 때 작은 쌍극자 모멘트가 생성되어 마이크로파에서 약한 회전 스펙트럼을 관찰할 수 있다.펙트 내시경 ^[10]검사

대칭 상판의 경우 전기-전자극 허용 순수 회전 전이에 대한 선택 규칙은 δK = 0, δJ = ±1이다.이러한 전환은 1 스핀의 단일 광자의 흡수(또는 방출)에 의한 것이므로, 각 운동량의 보존은 분자 각 운동량이 최대 1 ^[11]단위까지 변화할 수 있다는 것을 의미한다.또한 양자수 K는 +J~-^[12]J의 값을 가지도록 제한된다.

라만 스펙트럼

라만 스펙트럼의 경우 분자는 입사 광자가 흡수되고 다른 산란 광자가 방출되는 전이를 겪는다.이러한 전이가 허용되는 일반적인 선택 규칙은 분자 분극성이 이방성이어야 한다는 것인데, 이는 모든 ^[13]방향에서 동일하지 않다는 것을 의미합니다.편광성은 타원체로 표현될 수 있는 3차원 텐서이다.구면 꼭대기 분자의 편광성 타원체는 사실 구면이기 때문에 그 분자들은 회전하는 라만 스펙트럼을 보이지 않는다.다른 모든 분자의 경우 스토크선과 항스토크선을^{[notes 5]} 모두 관찰할 수 있으며, 많은 회전 상태가 열로 채워져 있기 때문에 비슷한 강도를 가진다.선형 분자에 대한 선택 규칙은 δJ = 0, ±2이다.이 값이 ±2인 이유는 ^[14]회전 중에 편광성이 같은 값으로 두 번 돌아오기 때문입니다.δJ = 0 값은 분자 전이가 아니라 입사 광자가 ^[15]방향을 바꾸는 레일리 산란과 일치한다.

대칭 꼭대기 분자에 대한 선택 규칙은 다음과 같다.

δK = 0

K = 0이면 δJ = ±2

K 0 0이면 δJ = 0, ±1, ±2

δJ = +1인 전이는 R 계열에 속하며, δJ = +2인 전이는 ^[15]S 계열에 속한다고 한다.라만 전이는 두 개의 광자를 포함하기 때문에 분자 각운동량이 두 단위까지 변할 수 있습니다.

단위

회전 상수에 사용되는 단위는 측정 유형에 따라 달라집니다.적외선 스펙트럼이 파장 번호 ${\displaystyle \stackrel{}{}}$(${\$ ~ {\$displaystyle {\nu }})$인 경우 단위는 일반적으로 cm로⁻¹ 표기되는 역센티미터 또는 문자 그대로 1cm 단위의 파장( ${\displaystyle \stackrel{}{~}}$ ~ $=$/${\displaystyle 1}${\ {$tilde {nu$}} = 1/1/1/1$\da)$입니다.한편 ${\displaystyle }$ 스케일( ${\$ \ $displaystyle \nu$)의 마이크로파 스펙트럼의 경우 단위는 보통 기가헤르츠입니다.이 두 단위 사이의 관계는 다음 식에서 파생됩니다.

$\displaystyle \nu \cdot \cdda = c,}$

여기서 θ는 주파수, θ는 파장, c는 빛의 속도입니다.따라서

${{displaystyle {tilde {nu}}/{\text{cm}}=paramfrac {1}{\text{cm}}=param frac {nu /{\text{s}{-1}}{c/\cdot \mathrm {s}^-1}\오른쪽)}}=beakfrac {{\text{s}^{-1}}{2.99792458\times 10^{10}}}.}$

1GHz = 10Hz이므로⁹ 수치 변환은 다음과 같이 나타낼 수 있습니다.

${\displaystyle\text{cm}{-1} 약 {\frac\nu/{\text}GHz}}{30}}.}$

진동이 회전에 미치는 영향

진동 들뜸 상태의 집단은 볼츠만 분포를 따르기 때문에 저주파 진동 상태는 실온에서도 상당히 채워집니다.진동이 들뜨면 관성모멘트가 높아지기 때문에 회전상수(B)가 감소한다.따라서 각 진동상태에서의 회전주파수가 서로 다르다.이로 인해 회전 스펙트럼에서 "위성" 선이 발생할 수 있습니다.예를 들어 시아노디아세틸렌, H-CcCcCnCnN을 ^[16]제공한다.

또한 회전(비관성) 프레임 내 핵의 진동운동 사이에 가상의 힘인 코리올리 결합이 있다.그러나 진동 양자수가 변화하지 않는 한(즉, 분자가 하나의 진동 상태에 있는 경우), 진동 시간은 회전에 필요한 시간보다 훨씬 짧기 때문에 회전에 대한 진동의 영향은 중요하지 않다.코리올리 커플링도 낮은 진동 및 회전 양자수에만 관심이 있는 경우 무시할 수 있는 경우가 많습니다.

회전의 진동 스펙트럼에 대한 영향

역사적으로 회전 에너지 준위의 이론은 적외선 분광학에서 가스의 진동 회전 스펙트럼 관측을 설명하기 위해 개발되었으며, 마이크로파 분광학이 실용화되기 전에 사용되었다.첫 번째 근사치에서는 회전과 진동을 분리할 수 있으므로 회전 에너지가 진동에너지에 가해진다.예를 들어, 선형 분자의 회전 에너지 수준은 (강체 회전자 근사에서)

$(\displaystyle E_{\text{rot}}=hcBJ(J+1))}$

이 근사치에서 전이의 진동 회전 파동은 다음과 같습니다.

${\displaystyle {\text{vib}}+B'J'(J'+1)-B'J'(J'+1)}$

$여기$서 B ${\$ { $displaystyle$ B$$} 및$$ $B{\displaystyle {}^{}}$ $′$ { $displaystyle$ B$$}는$$$$ 각각 상하의 진동 상태에 대한 회전 $상수$이고${\displaystyle {}^{}}$J$style$ { $displaystyle$ J$'}$ 및${\displaystyle {}^{}}$J$style$ { $displaystyle$ J'}는${\displaystyle {}^{}}$ 상하의 회전 양자수입니다.실제로 이 표현은 진동의 부조화 효과, 원심 왜곡 및 코리올리 ^[17]결합을 위해 수정되어야 합니다.

스펙트럼의 이른바 R가지에 대해서는 진동과 회전이 동시에 들뜨도록 J ${\displaystyle {\prime }^{}}$ $=$ ${\displaystyle {}^{}}$ ${\displaystyle +}$ +$$ {\$displaystyle$ J'=$J'+1}$이다.P 지점은 J ${\displaystyle {\prime }^{}}$ $=$ ${\displaystyle {}^{}-}$ - $({디스플레이스타일$J'=$J'-1})$이므로 회전에너지의 양이 손실되고 진동에너지의 양이 확보된다.순수 진동 천이인 ${\displaystyle \delta }$ J ${\displaystyle =}$ {\$displaystyle \Delta$ J$=0$은 스펙트럼의 Q 분기를 발생시킵니다.회전 상태의 열 모집단으로 인해 P 분기는 R 분기에 비해 강도가 약간 낮습니다.

적외선 측정에서 얻은 회전 상수는 마이크로파 스펙트럼 분석에서 얻은 회전 상수와 잘 일치하지만, 마이크로파 스펙트럼 분석에서는 일반적으로 더 높은 정밀도를 제공합니다.

회전 스펙트럼 구조

구면 톱

구형 꼭대기 분자는 순 쌍극자 모멘트가 없다.순수 회전 스펙트럼은 입사 광자의 전계에 의해 회전이 가속될 수 있는 영구 쌍극자 모멘트가 없기 때문에 흡수 또는 발광 분광법에 의해 관찰될 수 없다.또한 편광성은 등방성이기 때문에 순수한 회전 천이를 라만 분광법으로도 관찰할 수 없다.그럼에도 불구하고 회전 상수는 ro-vibrational spectroscopy에 의해 얻을 수 있다.이것은 분자가 진동 들뜬 상태에서 극성을 띠었을 때 발생합니다.예를 들어 메탄 분자는 구면상이지만 비대칭 C-H 신장 대역은 회전결합에 나타나듯이 적외선 스펙트럼에서 회전 미세구조를 나타낸다.이 스펙트럼은 또한 밴드의 비대칭 구조에서 코리올리 결합의 명확한 증거를 보여주기 때문에 흥미롭다.

선형 분자

강성 로터는 회전하는 분자의 모델을 구성하기 위한 좋은 시작점입니다.성분 원자는 강체 결합에 의해 연결된 점 질량이라고 가정한다.선형 분자는 단일 축에 놓여 있고 각 원자는 질량 중심 주위의 구면 위를 움직입니다.2개의 회전자유도는 분자축의 방향을 기술하는 구면좌표 θ와 θ에 해당하며 양자상태는 두 개의 양자수 J와 M에 의해 결정된다. J는 회전각운동량의 크기를 정의하며 M은 외부 전기나 m과 같이 공간에 고정된 축에 대한 구성 요소를 정의한다.불가지론 분야외부장이 없는 경우 에너지는 J에만 의존합니다. 강성 회전자 모델에서 분자의 회전 에너지 수준 F(J)는 다음과 같이 나타낼 수 있습니다.

${\displaystyle F\left(J\right)=BJ\left(J+1\right)\qquad J=0,1,2,...}$

$여기$서 B$(\displaystyle$ B$)$는 분자의 회전 상수이며 분자의 관성 모멘트와 관련이 있습니다.선형 분자에서 분자 축에 수직인 축 주위의 관성 모멘트는 고유하다. $즉{\displaystyle {}_{}}$, ${\displaystyle I_{}}$ B ${\displaystyle {}_{}}$ ${\displaystyle I_{}}$ C${\displaystyle {}_{}}$ ${\displaystyle I_{}}$ A $=$$$ {\$style I_{B$} =$I_{C}, I_{A}=0$ 따라서

${\displaystyle B={h\pi {8\pi ^{2}cI_{B}}}={h \over {8\pi ^{2}cI_{C}}}}$

이원자 분자의 경우

${\displaystyle I=m_{1}m_{2}}{m_{1}+m_{2}}}d^{2}}$

여기서₁ m과₂ m은 원자의 질량이고 d는 원자들 사이의 거리이다.

선택 규칙에 따르면 방출 또는 흡수 중에 회전 양자 수는 단일성에 의해 변화해야 한다. 즉, ${\displaystyle \delta }$ J ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ δ - ${\displaystyle {}^{\mathrm{}}}$δ${\displaystyle {\mathrm{}}^{}=}$ ±$$ {\$display$style \$Delta$ J =$J^{\prime$}-$J^{\prime$ 따라서 회전 라인의 위치가 지정된다.

$(\displaystyle\tilde\nu }_{J^{\prime }\left(J^{\prime }\right)=2B\left(J^{\prime }\prime }+Q)}$

$여기$서 J$({$ J$^{\prime\prime$}})는$$ 하위 레벨을 $나타내고{\displaystyle {}^{}}$ J$({$ J$^{\prime}})$는 전환에 관련된 상위 레벨을 나타냅니다.

이 다이어그램은 ${\displaystyle \delta }$ J$$\$displaystyle \Delta$ J$}$ $=$1 선택 규칙을 따르는 회전 전환을 보여 줍니다.점선은 이러한 전환이 실험적으로 관찰할 수 있는 피쳐에 어떻게 매핑되는지 보여줍니다.$인접$한 J ${\displaystyle {\prime \mathrm{}}^{}}$ ${\displaystyle {\mathrm{\prime }}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle J{}^{}}$ { $displaystyle$ J$^{\prime$ \$prime }{\left 화살표 }J^{\$prime$$}} 전이는$$ 관측된 스펙트럼에서 2B로 분리된다.주파수 또는 파수 단위를 이 플롯의 x축에도 사용할 수 있습니다.

회전선 강도

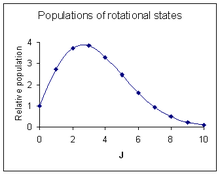
천이가 발생할 확률은 관측된 회전 선의 강도에 영향을 미치는 가장 중요한 요인입니다.이 확률은 전환에 관련된 초기 상태의 모집단에 비례합니다.회전 상태의 모집단은 두 가지 요인에 따라 달라집니다.양자수 J를 가진 들뜬 상태의 분자 수, 지면 상태의 분자 수 N_J/N은₀ 볼츠만 분포에 의해 다음과 같이 주어집니다.

$displaystyle$$$$T}}=e^{-{\frac {BhcJ(J+1)}{k$$T$

여기서 k는 볼츠만 상수, T는 절대 온도이다.이 인자는 J가 증가할수록 감소합니다.두 번째 요인은 2J + 1과 같은 회전 상태의 퇴화입니다.이 인자는 J가 증가할수록 증가합니다.두^[18] 요인 결합

${\displaystyle {text{population}}\propto(2J+1)e^{-{\frac {E_{J}}{k}T}}}}}}:$

최대 상대 강도는 다음 시간에 발생합니다^{[19][notes 6]}.

${\displaystyle J=sqrt\frac {k}T}{2hcB}}-{\frac {1}{2}}$

오른쪽 그림은 그 위의 스펙트럼에 대략 대응하는 강도 패턴을 나타내고 있습니다.

원심 변형

분자가 회전할 때 원심력은 원자를 떼어놓는다.그 결과 분자의 관성모멘트가 증가하여 강성로터의 식을 이용하여 계산했을 때 B$(\displaystyle$ B$)$의 $값$이 감소한다.이를 설명하기 위해 원심 왜곡 보정 항이 2원자 ^[20]분자의 회전 에너지 수준에 추가됩니다.

${\displaystyle F\left(J\right)=BJ\left(J+1\right)-DJ^{2}\left(J+1\right)^{2}\qquad J=0,1,2,...}$

$여기$서 D$(\displaystyle$ D$)$는 원심 왜곡 상수입니다.

따라서 회전 모드의 라인 위치는 다음과 같이 변경됩니다.

$(\displaystyle\tilde\nu }_{J^{\prime }\left(J^{\prime \prime }+1\right)-4D(J^{\prime \prime }+1\qad J^0\prime =1\prime)}$

그 결과, 강성 로터 근사처럼 선간 간격이 일정하지 않고, 회전 양자수가 증가함에 따라 감소한다.

이러한 표현에 기초하는 가정은 분자 진동이 단순한 조화 운동을 따른다는 것입니다.고조파 근사에서 원심 $상수{\displaystyle }$ D$(\displaystyle$ D$)$는 다음과 같이 도출할 수 있습니다.

${\displaystyle D=black {h^{3}}{32\pi ^{4}I^{2}r^{2}kc}}$

여기서 k는 진동력 상수입니다.$B$와$D$의 $관계{\displaystyle }$

$({displaystyle D=black {4B^{3}}}{\tilde {\tilde {\mega }}^{2}}})$

$여기$서 ${\displaystyle \stackrel{}{~}}$ ~$${\$displaystyle${\$tilde${{mega$}}}$은 고조파 진동 주파수입니다.부조화를 고려할 경우 J의 더 높은 거듭제곱의 항을 에너지 수준과 선 위치에 대한 ^[20]식에 추가해야 합니다.[J(J+1)]^5[21]까지의 조건에 적합된 플루오르화 수소의 회전 스펙트럼에 관한 두드러진 예가 있다.

산소

다이옥시겐 분자의
₂ 전기 쌍극자 모멘트 O는 0이지만, 분자는 두 개의 짝이 없는 전자로 상사성을 띠기 때문에 마이크로파 분광법에 의해 관찰될 수 있는 자기 쌍극자 전이가 허용된다.단위 전자 스핀은 주어진 분자 회전각 운동량 벡터 K에 대하여 세 가지 공간적 방향을 가지며, 따라서 각 회전 수준은 세 가지 상태, 즉 J = K + 1, K 및 K - 1로 분할되며, 이는 t의 회전 운동과 관련하여 스핀의 다른 방향에서 발생하는 이 소위 p형 세 개의 J 상태에서 발생한다.분자.이들 세쌍둥이에서 연속되는 J항 사이의 에너지 차이는 약 2cm⁻¹(60GHz)이며, 단, J = 1←0의 차이는 약 4cm이다⁻¹.자기 쌍극자 천이를 위한 선택 규칙은 트리플렛의 연속된 부재(δJ = ±1) 간의 천이를 허용하므로 회전 각 운동량 양자수 K의 각 값에 대해 2개의 천이가 허용된다.O핵은 핵 스핀 각운동량이 0이므로 대칭성을 고려할 때 K는 홀수 ^[22][23]값만 가져야 한다.

대칭 톱

대칭 로터의 경우 양자수 J는 분자의 총 각운동량과 관련된다.J의 주어진 값에 대해 양자수 M은 +J ...0 ... -J 값을 취하며, 세 번째 양자수 K는 분자의 주회전축에 대한 회전에 관련된다.외부 전계가 없는 경우 대칭 상단의 회전 에너지는 J와 K만의 함수이며, 강성 로터 근사에서는 각 회전 상태의 에너지는 다음과 같이 주어진다.

${\displaystyle F\left(J,K\오른쪽)=BJ\left(J+1\오른쪽)+\left(A-B\오른쪽)K^{2}\qquad J=0,1,2,\ldots\dots\mbox{and}\dots K=+J,\ldots,0,\ldots,-J}$

$여기$서 B ${\displaystyle =}$ ${\displaystyle h\frac{}{}}$ ${\displaystyle \frac{8\mathrm{}}{}}$ ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$ 2 ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \frac{I_{}}{}}$B {\$displaystyle$ B =${h$ \over ${8\pi ^{2}cI_$${$$B}}}}$ 및$$ $A{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle \frac{h\mathrm{}}{}}$ 8 ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$ 2 ${\displaystyle \frac{{cI}_{}}{}}$A {$displaystyle$ A = {$h \over {8\pi ^{2}cI_${}}}}}}$A$$}}}}:$ 프롤레이트 대칭 꼭대기 분자의 경우 $또는{\displaystyle }$ A$=$ 8 ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{c_{}}{}}$ I$$C {$displaystyle$ A={h$\over {8\pi ^{2}cI_{C}}}}:$ 타원형 분자의 경우.

이것에 의해, 다음과 같이 이행이 불안정해집니다.

$(\displaystyle\tilde\nu }_{J^{\prime},K}=F\left(J^{\prime},K\right)-F\left(J^{\prime},K\right)=2B\prime(J^{\prime}\prime)}$

선형 ^[24]분자의 경우와 같습니다.원심 왜곡에 대한 1차 보정을 통해 천이 파형은

$(\displaystyle\tilde\nu }_{J^{\prime},K}=F\left(J^{\prime},K\right)-F\left(J^{\prime\prime},K\right)=2\left(B-2D_{K})}$

D의_JK 항은 K 값이 서로 ^[25]다른 강체 로터 근사치에 존재하는 축퇴를 제거하는 효과가 있다.

비대칭 상단

양자수 J는 이전과 같이 총 각운동량을 의미한다.세 개의 독립적인 관성 모멘트가 있기 때문에 고려해야 할 두 개의 독립적인 양자수가 있지만 비대칭 로터의 용어 값은 닫힌 형태로 도출할 수 없다.각 J 값에 대해 개별 행렬 대각화를 통해 구합니다.공식을 사용할 수 있는 것은 대칭 ^[26]꼭대기에 가까운 모양을 가진 분자들입니다.

물 분자는 비대칭 팽이의 중요한 예이다.원적외선 영역에서 약 200cm⁻¹ 이하의 강렬한 순수 회전 스펙트럼을 가지고 있다.이러한 이유로 원적외선 분광계는 건조한 가스로 퍼징하거나 배기를 통해 대기 중 수증기를 제거해야 한다.스펙트럼은 ^[27]상세하게 분석되었다.

사극 분할

핵이 스핀 양자수를 가질 때, I는 1/2보다 크면 4극 모멘트를 갖는다.이 경우 핵 스핀 각 운동량과 회전 각 운동량의 결합은 회전 에너지 수준의 분열을 일으킨다.회전 수준의 양자수 J가 I보다 크면 2I + 1 레벨이 생성되지만 J가 I보다 작으면 2J + 1 레벨이 생성됩니다.그 효과는 초미세 분열의 한 종류이다.예를 들어 HCN에서 N(I = 1)이면 J > 0인 모든 레벨이 3으로 분할됩니다.부극성의 에너지는 핵 4극 모멘트와 F와 J의 함수에 비례한다. 여기서 F = J + I, J + I - 1, …, J - I. 따라서 핵 4극 분할 관측을 통해 핵 4극 모멘트의 크기를 ^[28]결정할 수 있다.이것은 핵 4극 공명 분광법의 대체 방법이다.회전 전환에^[29] 대한 선택 규칙은 다음과 같습니다.

$\displaystyle \Delta J=\pm 1,\Delta F=0,\pm 1)$

스타크와 지만 효과

정적 외부 전장이 존재할 경우 각 회전 상태의 2J + 1 축퇴가 부분적으로 제거되며, 이는 스타크 효과의 한 예이다.예를 들어, 선형 분자의 경우 각 에너지 수준은 J + 1 성분으로 분할됩니다.분열의 정도는 전계 강도의 제곱과 ^[30]분자의 쌍극자 모멘트의 제곱에 따라 달라집니다.원칙적으로 이것은 분자 쌍극자 모멘트의 값을 고정밀로 결정하는 수단을 제공한다.예를 들어 μ = 0.71521 ± 0.00020 debye인 황화카르보닐, OCS 등이 있다.그러나 분할은 μ에 따라² 달라지기 때문에 양자역학적 고려에서 ^[31]쌍극자의 방향을 추론해야 한다.

상사성 분자가 제만 효과의 한 예인 자기장에 놓일 때 축퇴의 유사한 제거가 일어날 것이다.기체상태에서 관찰되는 대부분의 종은 반자성체이다. 단, 질소산화물, 이산화질소, NO
₂, 일부 염소산화물, 수산기 등의 홀수전자분자는 예외이다.제만 효과는 다이옥시겐, O와
₂^[32] 함께 관찰되었습니다.

회전 라만 분광법

분자 회전 전이는 라만 분광법에 의해서도 관찰될 수 있다.회전 전이는 구면을 제외한 모든 분자를 포함하는 이방성 분극성을 가진 분자에 대해 라만 허용된다.이는 흡수나 방출에서는 관찰할 수 없는 영구적인 쌍극자 모멘트가 없는 분자의 회전 전이를 라만 분광학에서 산란함으로써 관찰할 수 있다는 것을 의미한다.푸리에 변환 적외선 분광계를 적용하면 매우 높은 분해능의 라만 스펙트럼을 얻을 수 있습니다.예를 들어 N의 스펙트럼이
₂ 있습니다.이는 핵 스핀의 효과를 나타내며, 인접 라인의 강도 변화는 3:1이다.결합 길이는 ^[33]109.9985 ± 0.0010pm으로 데이터에서 추론되었다.

기구 및 방법

현대 분광계들을 대다수의 사용자들은 그들의 특별한 요구에 따르면 통합하고 완벽한 맞춤형 사용 가능한 요소의 혼합물을 사용한다.omo는 광범위하게 그들의 일반 영업 원칙에 따라 분류될 수 있다.비록 회전 전환은 전자기 스펙트럼의 광범위한 지역 전역에서 발견되는, 기본적인 물리적 제약 조건 악기 구성 요소의 운용 대역 폭에 존재한다.그것은 종종고 비용이 드는 측정으로 전혀 다른 주파수 영역 안에 전환하는 것은 비현실적이다.는 계측기와 운영 교장 아래에 설명한 일반적으로 마이크로파 분광학 실험 주파수에서 624GHz사이의 조사에 적합하다.

흡수 셀 및 스타크 변조

마이크로파 분광계는 마이크로파 방사원, 샘플 가스를 도입할 수 있는 흡수 셀 및 슈퍼헤테로다인 리시버 등의 검출기를 사용하여 가장 간단하게 구성할 수 있다.투과된 방사선의 강도를 검출하면서 소스의 주파수를 스위프함으로써 스펙트럼을 얻을 수 있다.도파관의 간단한 섹션은 흡수 셀 역할을 할 수 있습니다.흡수 셀 내의 전극에 교류 전류가 인가되는 기술의 중요한 변화는 회전 천이 주파수를 변조하는 결과를 낳는다.이를 스타크 변조라고 하며 위상 민감 감지 방법을 사용하여 감도를 개선할 수 있습니다.흡수 분광법은 상온에서 열역학적으로 안정된 샘플을 연구할 수 있도록 한다.분자(NH
₃)의 마이크로파 스펙트럼에 대한 첫 연구는 1934년 ^[34]클리톤과 윌리엄스에 의해 수행되었다.그 이후의 실험은 2차 세계대전 동안 레이더용으로 개발된 클라이스트론과 같은 강력한 마이크로파를 이용했다.마이크로파 분광학 실험의 수는 전쟁 직후 급증했다.1948년까지, Walter Gordy는 약 100편의 연구 ^[35]논문에 포함된 결과에 대한 리뷰를 준비할 수 있었다.상업용^[36] 마이크로파 흡수 분광기는 1970년대에 휴렛 팩커드에 의해 개발되었으며 한때 기초 연구에 널리 사용되었다.현재 대부분의 연구소는 Balle-Flygare 또는 chirped-pulse Fourier transform 마이크로파(FTMW) 분광계를 사용하고 있습니다.

푸리에 변환 마이크로파(FTMW) 분광법

FTMW 스펙트럼 분석을 뒷받침하는 이론적^[37] 프레임워크는 FT-NMR 스펙트럼 분석을 설명하는 데 사용되는 것과 유사하다.진화하는 시스템의 동작은 광학 블로치 방정식으로 설명됩니다.우선 회전 천이를 수반하는 공진 시에 짧은 마이크로파 펄스(일반적으로 0~3마이크로초 지속시간)가 도입됩니다.이 펄스로부터 에너지를 흡수하는 분자는 입사 방사선과 위상적으로 일관되게 회전하도록 유도된다.분극 펄스의 비활성화는 분자 앙상블의 결손성을 수반하는 마이크로파 방출에 뒤따른다.이 자유 유도 감쇠는 계측기 설정에 따라 1-100마이크로초의 시간 척도에서 발생합니다.1950년대에 ^[38]Dicke와 동료들의 선구적인 작업에 이어 1975년에 ^[39]Ekers와 Flygare에 의해 최초의 FTMW 분광계가 구축되었다.

밸-플리가레 FTMW 분광계

Balle, Campbell, Keenan 및 Flygare는 FTMW 기술을 Fabry-Perot ^[40]공동이 포함된 진공 챔버로 구성된 "자유 공간 셀" 내에서 적용할 수 있음을 입증했습니다.이 기술을 사용하면 팽창하는 가스 제트의 목에서 샘플이 몇 켈빈까지만 급속 냉각된 후 몇 밀리초 동안만 프로빙할 수 있습니다.이는 (i) 분자를 저온으로 냉각시키는 것이 가용 인구를 가장 낮은 회전 에너지 수준으로 집중시키기 때문에 혁신적인 발전이었다.Fabry-Perot 공동을 사용함으로써 얻을 수 있는 혜택과 함께, 관측된 스펙트럼의 복잡성 감소와 함께 분광계의 감도와 분해능이 크게 향상되었다. (ii) 사용 가능한 에너지가 부족하기 때문에 매우 약하게 결합되어 있는 분자를 분리하여 연구할 수 있게 되었다.낮은 온도에서 파편화 또는 화학반응을 겪는다.William Klemperer는 약하게 결합된 상호작용의 탐구를 위해 이 기구를 사용한 선구자였다.Balle-Flygare FTMW 분광계의 Fabry-Perot 공동은 일반적으로 6GHz에서 18GHz 사이의 주파수에서 공명으로 튜닝할 수 있지만 개별 측정의 대역폭은 약 1MHz로 제한됩니다.애니메이션은 현재 마이크로파 분광학에서 ^[41]가장 널리 사용되는 도구인 이 기기의 작동을 보여줍니다.

채프 펄스 FTMW 분광계

는 digitisers와 관련 전자 제품 기술 면에서 두드러지FTMW 분광 법을 시작한 이후 계속 발전했다'고 언급하면서 이 B.H. 페이트 대학 Virginia[42]의 때(나는)에서 고속(4GS/s)임의의 wavefor의 사용 기술 혁신은 Balle-Flygare FT-MW 분광계의 많은 장점을 함유한 spectrometer[43]을 디자인했다.m발생기마이크로초 미만의 주파수로 최대 12GHz를 스위프하는 "치핑된" 마이크로파 편파 펄스를 생성하고 (ii) 고속(>40 GS/s) 오실로스코프를 사용하여 분자 자유 유도 감쇠를 디지털화하고 푸리에를 변환합니다.그 결과 약결합 분자를 연구할 수 있지만 Balle-Flygare FTMW 분광계에 비해 크게 향상된 측정 대역폭(12GHz)을 활용할 수 있게 되었습니다.원래의 CP-FTMW 분광계의 변형 버전은 미국, 캐나다 및 ^[44][45]유럽의 여러 그룹에 의해 제작되었습니다.계측기는 Balle-Flygare 설계에 의해 제공되는 고감도 및 해상도를 매우 보완하는 광대역 기능을 제공합니다.

메모들

레퍼런스

참고 문헌

외부 링크

• 적외선 가스 스펙트럼 시뮬레이터
• 회전 스펙트럼에 관한 하이퍼 물리 기사
• 전 세계 마이크로파 분광학 연구 그룹 목록